量子粒子群算法在配電網重構中的改進和應用

劉迪，張強，呂干云

(南京工程學院 電力工程學院， 南京 211167)

0 引 言

配電網重構是提升配電網經濟性和可靠性的主要方式，也是配電網優化分析的重要內容。

隨著分布式電源(DG)的飛速發展，大量的DG接入了配電網，這大大改變了配電網的電源輻射、潮流方向、電壓分布和網絡損耗等[1-2]，使得傳統方法不再適用。因此，有必要對含 DG的配電網重構問題進行研究。

因為人工智能算法處理復雜的非線性規劃[3]問題具有一定的優勢，因此很多國內外相關學者引入該類算法來解決含DG的配電網重構問題。文獻[4]采用“門當戶對”原則對遺傳算法進行改進，并將其應用于含DG的配網重構，克服了算法的早熟收斂問題；文獻[5]針對算法早熟現象，對基本螢火蟲算法進行改進，有效完成了含DG的配網重構；文獻[6]引入交叉變異操作完成對二進制量子粒子群算法的改進，并將其應用于含DG的配網重構，改善了算法的收斂能力。文獻[7]采用布谷鳥和粒子群混合算法，擴大了全局搜索范圍；文獻[8]采用一種粒子群和遺傳混合算法進行含DG的配網重構，增強了算法的收斂能力。

然而，上述文獻在配網重構模型和優化算法方面仍存在需要改進的地方。例如，在配網重構模型方面，大部分文獻未能同時兼顧系統經濟性和可靠性，僅以有功網損最小為目標函數；在優化算法方面，大部分文獻僅是對傳統算法的某一方面進行了改進，沒有較好地平衡全局收斂能力與算法收斂速度之間的關系。

基于此，文章以有功網損和電壓穩定性指標作為目標函數建立配電網重構模型，并對傳統算法在全局收斂性、收斂速度和編碼策略等方面進行了改進。算例表明，該方法適用于含多種DG類型的配網重構，能有效降低網損、改善節點電壓和降低電壓穩定性指標，且計算精度高，具有一定的實用性。

1 配電網重構的數學模型

文章以有功網損和電壓穩定性指標作為目標函數進行含DG的配電網優化重構。

1.1 目標函數

(1)有功網損。

有功網損的表達式如下：

(1)

式中n為支路總數；i表示支路l的首端節點編號；Rl表示支路l的電阻；Kl表示支路l的開合狀態，閉合時取1，斷開時取0；Ui、Pi和Qi分別是支路首端節點i處的電壓、注入有功和無功功率。

(2)電壓穩定性。

由于DG的接入，配電網的電壓穩定性會受到某些程度的影響，因此有必要對電壓穩定性指標進行分析[9]。其表達式如下：

(2)

式中R和X分別是支路電阻和電抗；i和j分別表示支路的首端節點和末端節點編號；Pj和Qj分別是支路末端節點j注入的有功和無功功率。通過式(2)和潮流計算，可以得到所有支路的Ustabl，取最大的Ustabl作為整個系統的穩定性指標f2，即:

f2=max(Ustab1,Ustab2,…,Ustabn)

(3)

當系統負荷極具增大時，對應f2的支路最容易首先發生電壓崩潰。因此，f2越小，電壓穩定性越好；反之則越差。

(3)綜合目標函數。

對f1和f2進行歸一化處理并構建目標函數[10]，其數學表達式如下：

(4)

式中f01和f02分別表示配電網重構前的有功網損和電壓穩定性指標；a和b分別為兩個指標的懲罰因子；w1和w2表示上述兩個指標的權重系數。權重系數可以根據需要人工調節，當w1=1且w2=0時，以有功網損為唯一優化目標；當w1=0且w2=1時，以電壓穩定性為唯一優化目標。

其中，懲罰因子a和b的計算公式如式(5)和式(6)所示。

(5)

(6)

式(5)中，當系統重構后的有功網損大于初始值時，則表明該方案不可行，a取一個較大正數N(文章設置為10)，等同于賦予無效解較大網損，使其在迭代過程中不占優勢從而被淘汰；反之，a取1。懲罰因子b的取值方法同a。此處不再贅述。

1.2 約束條件

(1)潮流方程。

(7)

式中Pi和Qi分別是節點i處電源節點注入的有功和無功功率；PDGi和QDGi分別是節點i處DG注入的有功和無功功率；PDi和QDi分別是負荷節點i處的有功和無功負荷功率；m為節點總數；Gij、Bij、δij分別是節點i、j之間的電導、電納和相角差。

(2)支路功率。

(8)

式中Sl和Slmax分別為第l條支路的傳輸功率和最大允許功率；PDGmin和QDGmin分別表示DG的有功和無功功率下限；PDGmax和QDGmax分別表示DG的有功和無功功率上限。

(3)節點電壓。

Uimin≤Ui≤Uimax

(9)

式中Uimax和Uimin分別表示節點i的電壓最大值與最小值。

(4)網絡拓撲約束。

重構后的配網結構要求呈輻射狀且無環網與孤島。

2 分布式電源的潮流計算模型

根據DG并網方式[11-12]的不同可將其分為以下四類：

(1)PQ節點類型。

如雙饋型風機等恒功率因數運行的DG可視作PQ節點。此類DG在潮流計算時，將其看成負的負荷，其潮流計算等效模型為：

(10)

式中Ps和Qs分別表示DG輸出的有功和無功功率。

(2)PV節點類型。

如燃料電池等通過同步機或經過電壓控制逆變器并網的DG可視作PV節點[13]。此類節點在潮流計算時由于不滿足前推回代法的條件，需對其作出如下處理：

(11)

式中 ΔQ和ΔU分別表示無功功率修正量和電壓修正量；U和X分別表示DG的電壓幅值和電抗矩陣；Qt-1和Qt分別表示第t-1次和第t次迭代的無功功率。

為了避免修正后發生無功越限的情況，需對式(11)作出如下修改：

(12)

式中Qmax和Qmin分別表示DG無功功率的上、下限。

因此其潮流計算等效模型為：

(13)

式中Ut-1表示第t-1次迭代的電壓幅值。

(3)PI節點類型。

如光伏電站等采用電流控制逆變器并網的DG可視作PI節點。此類節點在潮流計算時由于不滿足前推回代法的條件，需對其作出如下處理：

(14)

式中Is表示DG注入電網的電流幅值；Ut-1表示第t-1次迭代的節點電壓。

在潮流計算的過程中，通過式(14)求得PI節點的無功功率，從而將PI節點轉化為PQ節點，其潮流計算等效模型為：

(15)

(4)PQ(V)節點類型。

采用異步發電機作為接口并入配電網的DG可視作P恒定，V不定，Q隨著P、V的變化而改變的PQ(V)節點，其潮流計算等效模型為：

(16)

3 基于改進量子粒子群算法的配電網重構

3.1 編碼策略

配電網多采用環狀結構輻射狀運行，即每閉合一個聯絡開關就會形成一個環網。為了滿足配電網運行的結構要求，就必須斷開該環網內的一個分段開關使網絡維持輻射狀。由于配電網支路眾多，因此選擇一種合理的支路編碼策略十分必要。為了降低配網重構的解空間，文章采用十進制環狀編碼策略[14]對各支路進行編碼。具體步驟如下：

(1)閉合全網開關，形成若干環網，環網個數等于聯絡開關數；

(2)對全網開關從小到大進行自然數編號，并將其按照各自所屬的環網歸類；

(3)對各環網內的開關重新進行環內編號，各環網內的聯絡開關最后編號。

下面以圖1所示的IEEE 33節點系統為例進行編碼說明，編碼結果見表1。

圖1 IEEE 33節點系統

如圖1所示，網絡中有32個分段開關和5個聯絡開關，其中1號開關不在任何環網內，所以不對其進行編碼。該編碼策略中，粒子維數即環網個數，每一維的具體數值表示相應環網內斷開的開關號。例如，粒子Swarm=[2,2,4,13,10]表示斷開開關6,13,8,25,3。由表1可知，粒子各維的上限為Ub=[10,7,15,21,11]，下限為Lb=[1,1,1,1,1]。

由于配網中各環網間公共支路眾多，僅采用上述編碼策略可能不滿足配電網的拓撲約束，因此還需要對所產生的解進行拓撲檢測。文章采用節點分層前推回代法[15]進行潮流計算，潮流計算方法如下：

(1)根據配電網的支路與節點參數推導并生成節點分層矩陣LayerM和其上層節點矩陣NU；

(2)根據LayerM和NU，從最后一層向上一層前推求解各支路電流；再從第一層向下一層回代計算各節點電壓；

(3)迭代滿足條件后，根據各節點電壓求解各支路潮流。

文章借助支路-環路矩陣F以及潮流算法中需要生成的矩陣LayerM和NU來進行環網和孤島檢測。若檢測為可行解，則可直接通過已生成的LayerM和NU進行后續的潮流計算，大大節省了運算時間，提高了運算效率。具體步驟如下：

(1)粒子反編碼，即將粒子環內編號轉換為實際開關號；

(2)根據粒子生成F矩陣，若F為對角陣，則粒子為可行解；反之則進行環網檢測；

(3)若F為非對角陣且有2行相同，則存在環網，粒子為不可行解；反之則進行下一步孤島檢測；

(4)根據粒子生成LayerM和NU矩陣，若NU中只有首列元素(電源所在列)為0，則粒子為可行解；反之則存在孤島，粒子為不可行解。

仍以粒子Swarm=[2,2,4,13,10]為例說明，對其進行反編碼并生成如下3個矩陣：

LayerM=

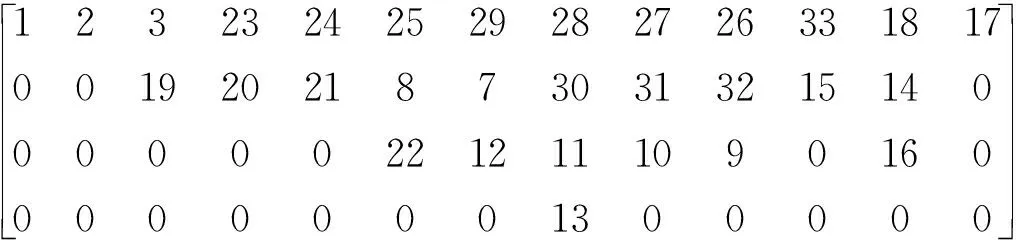
NU=[0 1 2 0 0 0 8 21 10 11 12 22 12 15 9 15 18 33 2 19 20 21 3 23 24 27 28 29 25 29 30 31 32]。

F為非對角陣且無兩行相同，故不存在環網；從LayerM中可以看出網絡分為了13層，其對應的NU除了首列元素外，第4、5、6列也為0，則表明節點4、5、6形成了孤島，故該粒子為不可行解。

3.2 傳統算法

粒子群算法(PSO)是一種基于生物群體智能的進化理論[16-17]。針對其計算精度不高、局部收斂等缺點，文獻[18]提出了量子粒子群算法(QPSO)。

和PSO算法不同的是，QPSO算法舍棄了速度更新，僅保留了位置更新，大大降低了參數調節的復雜度，增強了全局收斂能力[19-20]。其更新公式如下：

(17)

式中Pbest_c、Gbest、Mbest分別表示粒子c的局部最優位置、全局最優位置和平均最優位置；pc表示局部吸引點；φ和u均表示(0,1)區間內均勻分布的隨機數，當u>0.5時，取負號，反之取正號；M表示種群規模；x(t)和x(t+1)分別表示第t次和第t+1次迭代粒子的位置；β表示收縮擴張系數，是QPSO算法中除了迭代次數和種群規模以外唯一需要人工調節的參數，一般按下式取值：

(18)

式中t表示當前迭代次數；maxiters表示最大迭代次數。

3.3 改進算法

QPSO算法擴大了粒子搜索空間，一定程度上提高了計算精度，但仍存在早熟收斂、計算效率低等問題。因此，文章對QPSO算法進行了幾點改進。

3.3.1 基于十進制編碼的改進策略

QPSO一般采用連續編碼，迭代后生成的結果為連續實數[21]，而文章采用十進制編碼策略，粒子各維分量必須滿足正整數的要求。因此需對式(17)中的x(t+1)作出如下改進：

(19)

式(19)中，函數round( )表示四舍五入取整。

此外，由于粒子各維的上下限不同，因此粒子在可行域內搜索往往會越限。為此，文章還需對粒子越限情況作出補充：

(20)

式中xc,g表示粒子c的第g維分量；Ub,g和Lb,g分別表示粒子第g維的上下限；函數roundint()表示在區間[Lb,g,Ub,g]內隨機產生一個整數。

3.3.2 基于錦標賽選擇的改進策略

由式(17)可知，在QPSO算法中，吸引子pc是由局部最優位置Pbest_c和全局最優位置Gbest共同決定的，但如果此時的Gbest位于次優解領域內，并且離真正的全局最優解較遠時，粒子向Gbest收斂則可能導致早熟。為了避免產生早熟收斂現象，文章在QPSO算法中加入了遺傳算法中的錦標賽選擇策略。

在基于錦標賽選擇操作的改進策略中，通過引入一個選擇因子T，使得隨機選擇粒子k的個體最好位置pk與當前粒子的位置Pbest_c產生競爭，即每次隨機從種群中選擇一個粒子，計算其適應度值，并與當前粒子的適應度值相比較，如果好于當前粒子的適應度值，則pc由Pbest_c和pk決定；反之，則pc由Pbest_c和Gbest決定。

T的計算公式如下：

(21)

式中f(pk)和f(Pbest_c)分別表示粒子k和粒子c的適應度值。

用式(21)代替式(17)中的Gbest，得改進后的pc坐標公式為：

pc=φ×Pbest_c+(1-φ)×T

(22)

3.3.3 基于混沌擾動的改進策略

文章引入Logistic公式將混沌優化與QPSO算法結合, 利用混沌搜索的隨機性和遍歷性，使得初始種群的的分布更具均衡性和多樣性，并擾動適應度值較差的部分粒子，從而增加粒子局部搜索精度，加快收斂速度。Logistic映射公式如下：

Zh+1=μZh(1-Zh)

(23)

式中 一般μ取4時，混沌序列無重復現象；Zh為(0,1)區間內隨機數。

擾動適應度值較差粒子的具體步驟：

(1)按照適應度值大小對粒子進行排序，選出適應度值較差的30%的粒子；

式(24)中，xc和x′ >c分別表示擾動前后粒子的位置；α為擾動系數，取α=2。

(2)利用式(23)多次迭代產生d個不同的混沌變量Zh，d表示搜索空間維數(本文d取5);

(3)對選出的粒子的每一維進行不同的擾動，擾動公式如下：

(24)

(4)計算擾動后粒子的適應度值，若其優于擾動前，則更新粒子位置；反之則保持不變。

改進初始種群的具體步驟：

(1)在搜索空間內隨機生成一個初始粒子，記其位置為x0；

(2)對粒子x0進行歸一化處理，得混沌序列的初始值Z1為：

(25)

式中xmax和xmin分別表示搜索空間的上、下界。

x′>0=xmin+Zh(xmax-xmin)

(26)

4 計算流程

將第3節所述算法應用于配電網重構，其具體流程如圖2所示。

圖2 改進算法流程圖

5 算例仿真

文章采用如圖1所示的IEEE 33節點系統進行算例分析。系統電壓基準值為12.66 kV，功率基準值為10 MV>·A，有功負荷為3 715 kW，無功負荷為2 300 kvar。

采用改進算法對仿真算例進行網絡重構，取M=50，maxiters=100。由于改進的量子粒子群算法中把粒子適應度值最大定義為最優解，所以文章將式(4)的倒數定義為適應度函數，即：

(27)

5.1 不含DG的配電網重構

為了證明改進后算法的合理有效，在不含DG的情況下，僅以有功網損作為目標函數，分別采用改進算法、QPSO算法和文獻[22]算法進行配電網重構，重構結果和算法收斂曲線見表2和圖3。

表2 不含DG重構結果

圖3 算法收斂曲線

由表2可以看到，重構前，系統有功網損為202.647 1 kW，最低節點電壓為0.913 3 p.u.；采用改進算法重構后，系統有功網損從初始值降低到了139.473 1 kW，降損率達到 31.17%，最低節點電壓也從0.913 3 p.u.提高到了 0.947 9 p.u.。

與文獻[22]算法相比，改進算法在減小網絡有功損耗和提高節點電壓方面均具一定的優勢；與QPSO算法相比，雖然改進算法的優化結果與其相同，但由圖3可知，QPSO算法中后期的尋優能力低下，容易導致局部收斂，而改進算法由于采用錦標賽選擇和混沌擾動策略引導算法尋優，可使粒子快速跳出次優解，只需迭代6次即可收斂到最優解，加快了收斂速度。

圖4是重構前、后電壓分布曲線，可以看到，利用改進算法重構后，不僅能有效降低系統網損，還能在整體上改善節點電壓分布，提高節點電壓水平。

圖4 不含DG重構后節點電壓變化曲線

5.2 含DG的配電網重構

為了驗證改進量子粒子群算法是否適用于含多種DG類型的配電網重構，文章選取了4種不同類型的DG，按照文獻[23]設置的參數及位置并網，以有功網損和電壓穩定性指標作為目標函數進行配電網重構，并將重構結果與文獻[23]進行對比分析。DG并網參數如表3所示，重構結果和節點電壓變化曲線分別如表4和圖5所示。

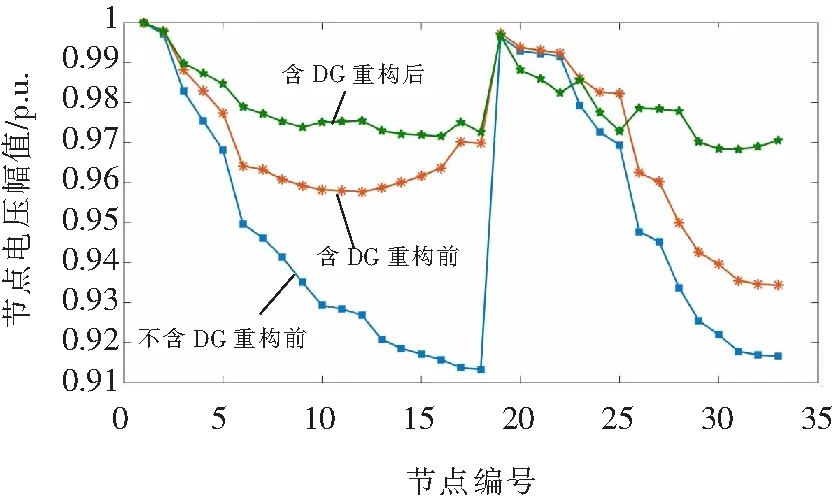
圖5 含DG重構后節點電壓變化曲線

表3 DG并網參數

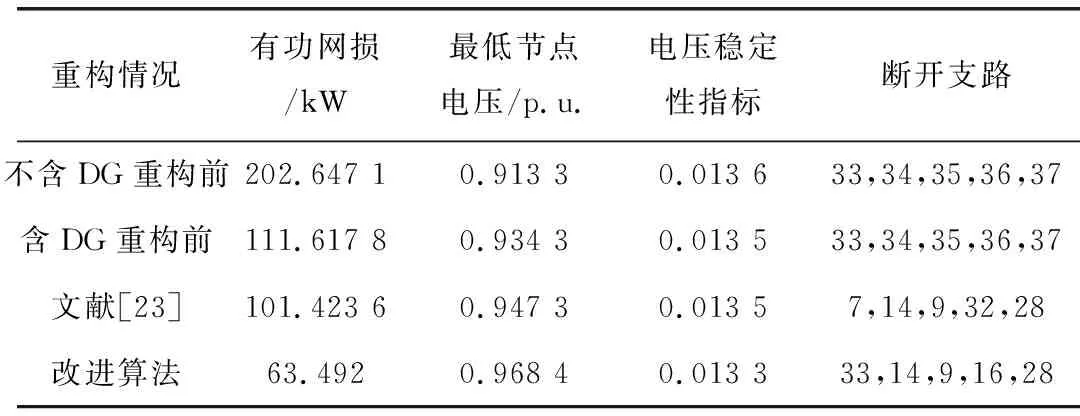
表4 含DG重構結果

從表4可以看出，未接入DG時，系統網損為202.647 1 kW；接入DG后，有功網損降低至111.617 8 kW，比初始網損降低了44.92%。同時，最低節點電壓從0.913 3 p.u.提高到了0.934 3 p.u.，電壓穩定性指標也從0.013 6降低至0.013 5。由此可以看出，接入一定容量的DG能夠降低系統網損、提高節點電壓和減小電壓穩定性指標。

采用改進算法重構后，系統網損降低至63.492 kW，與不含DG的初始網絡相比，有功損耗降低了68.67%；與含DG的初始網絡相比，有功網損降低了43.12%。同時，重構后的最低節點電壓提高到了0.968 4 p.u.，電壓穩定性指標也降低至0.013 3。可以看出，重構后的系統網損和電壓穩定性指標明顯下降，節點電壓水平大大提高。由此表明，文章所提方案能夠顯著提高系統的經濟性和可靠性。與文獻[23]相比，改進算法得到的重構方案在有功網損、節點電壓和電壓穩定性指標三個方面均具有一定的優勢。

此外，由圖5可知，采用改進算法重構后的系統節點電壓分布較為均勻，且電壓穩定性更好。

6 結束語

針對大量DG接入配網的現狀，文章提出了一種基于改進QPSO的配電網重構方法。將遺傳算法中的錦標賽選擇策略與QPSO算法相結合，提高算法全局收斂能力，并通過混沌公式改進初始種群和擾動適應度值較差粒子，增加局部搜索精度，加快收斂速度，從而較好地平衡了全局收斂與計算效率之間的關系。此外，該算法還增加拓撲檢測環節來降低不可行解的產生概率，提高運算效率。算例表明，采用該方法進行含DG的配網重構，不僅能有效地降低網損、改善節點電壓和降低電壓穩定性指標，且收斂速度快、精度高，為進一步研究含DG的配電網動態重構提供了參考和借鑒。