面向細紗機多元性能退化過程的可靠性評估方法

邵景峰，董夢園,牛一凡,陳可心

(西安工程大學 管理學院，陜西 西安 710048)

0 引 言

準確評估紡織設備的工作狀態，對于紡織行業充分利用生產能力、提高生產效率有著重要的意義。細紗機是是決定紗線質量的核心設備。細紗機作為一種大型復雜機電一體化設備，不僅內部結構復雜，涉及零配件和關鍵器材專件眾多，而且具有高可靠性、長壽命等特點。如1臺1 200錠的細紗機，涉及60多個關鍵器材專件、107 029個零件以及100多個溫度、濕度、振動傳感器。然而，細紗機在工作過程中受各種因素的交替作用和相互影響，致使其性能退化，這種退化又對成紗質量產生了嚴重影響。因此，如何對細紗機性能退化過程進行可靠性評估是一個亟待解決的問題。

對于細紗機性能退化的可靠性評估，目前多聚焦在細紗機的部分結構或細紗機的工藝參數評估。吳入軍等從細紗機的部分組成結構入手，探討牽伸機構中齒輪因磨損過大而損壞問題[1]，優化了細紗機的牽伸結構，提高了自身的可靠性；CUI等從牽伸系統的改進出發以提高成紗質量，研究了常規牽伸系統與改進型牽伸系統的不同之處，以及工藝參數對細紗機的影響[2]；HE等利用流體力學軟件模擬和表征細紗機的運動，使紗線性能得到了提高[3]；LI等將可靠性增長系數與蒙特卡羅仿真模型相結合，建立了細紗機的可靠性評估模型[4]。目前已經解決了基于設備失效時間分析可靠性分布規律、建立可靠性指標以及故障頻率的預測問題。

有的學者從細紗機內部故障角度入手，探討細紗機運行狀態的監控。文獻[5]根據監控紡紗機的運行情況，實現了羅拉、鋼領板和錠子等運動部件獨立驅動的細紗機控制系統，提高了采集速率及數據傳輸的穩定性。眾多的研究著眼于利用時域分析、小波變換和功率譜分析等方法實現細紗機正常運行與故障數據的采集；從零部件角度入手，探討了細紗機故障辨識，已經解決了提取故障信息的特征參數的問題。宋曉亮等研制了一種光電反射式故障診斷器，解決了運動過程難以監控的問題[6]；王延年等利用改進神經網絡的方法，降低了錠子轉速波動，解決了細紗機錠子速度變化使細紗卷繞過程中斷頭率高的問題[7]。隨著機電一體化技術的發展，學者們的研究聚焦在數據驅動的可靠性評估方面：通過建立復雜系統性能退化模型，對細紗機進行壽命預測和可靠性評估[8]。SI等利用Wiener 模型描述退化過程，并給出了對應的剩余壽命分布和可靠性函數解析形式[9]；LI等對隨機過程中的維納過程進行了深入的研究，推導并驗證了模型中的隨機參數[10]；趙廣社等驗證Wiener 模型，得到了較高的預測精度，為以后的研究提供了很好的理論基礎[11]。

可見，人們的研究角度主要集中在細紗機運行數據采集以及部分結構的可靠性預測方面，忽略了設備在運行過程中的隨機因素對設備使用壽命的影響，而且主要利用單一表征參數衡量設備退化軌跡，對多個指標的性能退化狀態信息不能充分利用。此外，還存在如何充分利用監測到的信息對細紗機進行性能退化建模進而對可靠性進行評估問題，其中的瓶頸在于細紗機的關鍵性能參數難以識別以及性能退化模型難以建立。為此，本文提出一種面向細紗機多元性能退化過程的可靠性評估方法，為細紗機維修管理提供支持。

1 性能特征參數篩選

細紗機的性能退化過程常被視為一個隨機過程[12]。在這個過程中，為了實現對細紗運行狀態的監測，往往需要采集細紗機的許多傳感器數據[13]。但問題是，因為其具有高維、隨機性的特點，并非所有監測到的數據都能表征細紗機的性能變化。為了解決這一問題，引入主客觀綜合權重對細紗機的關鍵特征參數進行識別。具體過程如下：首先，利用序關系分析法[14]比較細紗機性能退化的特征參數的重要度，根據專家經驗對參數重要程度排序，進而確定相鄰兩參數間的相對重要性，然后得到各個參數的權重系數pj。計算公式如下：

(1)

(2)

式中：pj為得到的第j個特征參數的權重值;pj+1為得到的第j+1個特征參數的權重值；yj為特征參數的重要度。但是，yj的計算結果易受主觀因素的影響而產生偏離，故引入熵權法進行綜合權重計算，具體的計算公式為

(3)

(4)

(5)

為了提高權重評價結果的準確性，利用最小二乘法，構建面向細紗機性能退化的指標權重?，如式(6)所示：

(6)

式中：?j為待求的綜合權重。在此基礎上，選擇綜合權重大于0.5的參數，作為細紗機性能退化的表征參數，并將該參數應用于細紗機自身性能退化的全過程[15]。

2 多元參數退化過程統計分析

2.1 Wiener過程的性能退化建模

利用Wiener隨機過程，對細紗機因自身磨損造成的性能退化過程加以描述[16]，構建的細紗機性能退化模型，如式(7)所示：

(t)=X(0)+μt+σβ(t)

(7)

式中：X(0)為初始性能退化量，通常設定X(0)=0；μ為飄移系數；β(t)為標準布朗運動；σ為擴散系數。設細紗機的壽命為T，失效閾值為ω，則細紗機的性能退化軌跡可由式(7)的Wiener過程進行描述。由此，細紗機的壽命T可定義如下：

T={t:X(t)≥ω|X(0)<ω}

(8)

由式(8)可知，細紗機壽命T達到失效閾值ω的時間服從逆高斯分布[17]：

(9)

(10)

式中：fT(t)為壽命T的概率密度函數；Rw(t)為細紗機單一過程的可靠性函數。

記ΔXi=Xti-Xtt-1,Δti=ti-ti-1。由Wiener過程的性質可知，細紗機性能退化增量之間相互獨立，而且服從正態分布ΔXi～N(μΔti,σ2Δti)。于是，通過細紗機的性能退化數據，可得到似然函數：

(11)

通過式(11)，對漂移系數和擴散系數求偏導。令偏導為零并對方程求解，從而得到μ和σ2的估計值：

(12)

(13)

2.2 多退化過程的可靠性建模

Copula函數為求解基于多種退化過程的細紗機可靠度評估模型提供了便利條件。現假設細紗機的失效閾值為ωj，當第j個退化過程的退化量Xj(t)超過其對應的失效閾值ωj時，細紗機發生退化失效[18]。由此，細紗機性能退化過程對應的可靠性表示為

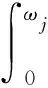
式中:f(Xj(t))為第j個退化過程對應的概率密度函數。在此基礎上，進一步構建多元退化相關失效可靠性模型R′(t)，如式(14)所示:

(14)

為便于分析細紗機多元退化的相關性問題，利用Copula函數進行細紗機多元退化相關性的建模[19]。設細紗機的性能退化量為X1(t)、X2(t)，與其對應的性能退化函數為FX1(t)、FX2(t)，則{F(X1(t)),F(X2(t))}的聯合分布函數可表示為

(15)

{F(X1(t)),F(X2(t))}的聯合密度函數為

h(X1(t),X2(t);θ)=C(FX1(t),FX2(t);θ)·

fX1(t)fX2(t)

(16)

在常見的Copula函數形式中，選擇合適的函數(t-Copula、 Gaussian Copula、 Clayton Copula、 Frank Copula、和Gumbel Copula)進行相關性分析。由于細紗機性能退化復雜，在相關性建模后變得更加復雜，而且未知參數較多。為此，利用基于貝葉斯理論的Gibbs算法[20]進行參數估計： 將2個過程所有的未知參數設為ξ，則ξ為一個n維向量，即ξ=(ξ1,ξ2,…,ξn)，對應的先驗分布為p(ξ1,ξ2,…，ξn)。具體步驟如下:

3 實驗驗證

3.1 參數選擇

可以通過直接分析細紗機在運行時的各種參數，如羅拉轉速、錠子速度的變化表征細紗機的運行狀態。比如，羅拉是細紗機上壓住紗條或纖維的滾動長軸或短軸。羅拉速度不穩定，容易造成羅拉纏花，導致紗線斷頭，可以通過間接分析捻度平均值、管紗長度等成紗結果表征。又比如，細紗捻度不勻率過大會影響紗線單紗強力以及條干不均率，造成坯布布面黃白檔等疵點，布面染色時會因為吸色性能差異而產生明顯的色差等質量問題。

依托課題組在咸陽紡織集團安裝的“紡織廠生產信息管理系統”，根據生產參數和生產數據計算出細紗捻度、牽伸倍數、輪班產量、累計產量、效率等指標并在終端顯示。研究過程中，可以對細紗機當班生產數據(包括前羅拉速度、后羅拉速度、停機次數、停機時間、 車速、牽伸倍數、捻度、品種、號數、實際產量、開臺效率等)進行瀏覽、查詢以及統計分析。在此基礎上，選擇了如表1所示的細紗機運行參數。在成紗過程中，當實際監測的運行參數與設定的工藝參數之間數值不一致時，被認定為細紗機性能發生了退化。

表 1 細紗機運行狀態參數

由于并非所有監測到的數據都能表征細紗機的性能變化，因此根據上述的序關系法與熵權法相結合的方法，計算表1中的15個參數的綜合權重。選取綜合權重大于0.5的參數，形成的監測參數綜合權重變化，如圖1所示。

圖 1 細紗機性能參數篩選Fig.1 Screening of performance parameters of spinning frame

由圖1可知，序號為4(錠子速度)、11(后羅拉轉速)的參數權重大于0.5。因此，選取錠子的速度偏差和后羅拉轉速偏差作為細紗機性能退化參數。

為了驗證所選取參數能夠較好的表征細紗機的性能退化，監測2個參數的變化對成紗質量的影響。邵景峰[21]在研究中驗證，在整個紡紗過程中有5個指標(條干不勻、粗節、細節、斷裂強度和斷裂伸長)易受各類異常因素的影響，其中“斷裂強度”最為顯著。因此,監測錠子速度、后羅拉轉速等2個參數的變化對“斷裂強度”的影響,結果如圖2所示。

圖 2 斷裂強度變化Fig.2 Variation of fracture strength

由圖2可知，在2個指標的影響下斷裂強度一直在降低，與實際過程中相對應。隨著細紗機錠速的增加，紗線張力也會隨著錠速的提高而相應的增加。如果錠速過高，會使紗線從羅拉到導紗鉤處出現抖動，影響后羅拉的速度，導致羅拉纏花，使紗線斷裂強度降低、紗線斷頭。實驗結果表明，選擇這2個參數作為細紗機的性能變化的參數是可行的。

3.2 算例驗證

選取指標為錠子速度和后羅拉轉速，對采集到的數據進行仿真，結果如圖3所示。同時，得到兩者之間的散點圖，如圖4所示。

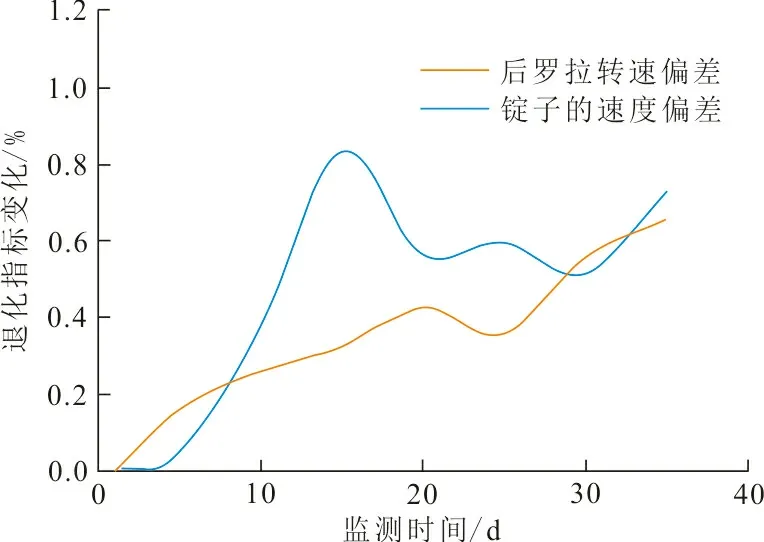
圖 3 數據偏差仿真結果Fig.3 Simulation results of data deviation

由圖3和圖4大致可以看出來，隨著成紗過程的不斷推移，錠子速度增加，后羅拉轉速也在增加。為了進一步驗證兩者之間的相關關系，在實際紡紗過程中對其進一步實驗。借助Copula函數的優點，分別選擇Copula函數的4種不同形式進行細紗機性能退化過程的參數估計，同時進行AIC準則的檢驗，結果如表2所示。AIC值越小，說明函數擬合效果越好，同時可得到不同Copula函數對應的參數θ估計值。

圖 4 數據散點Fig.4 Scatter plot of data

表 2 Copula函數AIC值

從表2可以看出，Clayton Copula函數的AIC值最小，故選用此函數進行相關性建模。利用Clayton Copula函數仿真得到的概率密度函數和聯合分布函數如圖5、圖6所示。由圖5、6可知，2種退化過程之間具有一定的相關性。

圖 5 概率密度函數Fig.5 Probability density function

圖 6 聯合分布函數Fig.6 Joint distribution function

在此基礎上，進一步利用相應的可靠性函數，對細紗機多元參數的可靠度進行仿真實驗，得到如圖7所示的多元參數相關可靠度曲線。

圖 7 細紗機多元參數相關可靠度曲線Fig.7 Multivariate parameter correlation reliability curve

由圖7可知，當監測時間小于10 d時，多元參數退化失效的可靠度趨近于1；當監測時間在10～20 d區間時，其可靠度迅速下降；當監測時間超過30 d時，其可靠度趨于零。這一結果說明：當監測時間在10～20 d區間時，多元參數退化失效的可靠度偏差大。企業在這期間應該進行維修。

4 結 語

針對細紗機的關鍵性能參數難以識別以及性能退化模型難以建立問題，分析細紗機性能特征，并篩選細紗機的監測參數，得到了關鍵性能參數。在此基礎上，利用Copula函數探討多種退化參數之間的相關性，利用Wiener隨機過程描述了多元退化失效過程,較好地描述了細紗機的退化軌跡。利用最大似然估計以及貝葉斯理論的Gibbs算法估計參數，以此構建了面向細紗機多元性能退化過程的可靠性評估模型。依托細紗機的監測數據，進行了模型驗證和對比分析，結果表明，構建的模型能夠較好的表征細紗機可靠度變化。說明模型具有較高的準確性，有利于細紗機的可靠性評估，為細紗機的維修管理提供支持，進而提高紡紗質量。