旋轉輪胎中壓電懸臂梁離心距優化

張云順，趙香帥，王萬樹

(1. 江蘇大學 汽車工程研究院，江蘇 鎮江 212013；2. 筑波大學 系統信息工程學院，日本 筑波 3058573)

0 引言

隨著微電子處理技術的發展，無線傳感器已廣泛應用于各種設備中，但如何為無線微傳感器提供永久電源是目前面臨的主要問題[1]。近年來，壓電式振動能量采集器大多采用懸臂梁結構，其理論分析模式是基于線性結構存在頻率響應單一性問題。Leadenham等[2]利用非線性系統將激勵與諧振子間的耦合擴展到寬頻帶區域，以拓寬振動能量采集器的有效頻率范圍，但在低頻區域提高采集器性能較難。

隨機共振是指在弱周期信號中加入噪聲，在一定概率內顯著放大輸出響應的現象。這一現象已被用于信號檢測和故障診斷[3-4]、圖像處理[5]和生物神經分析[6]等。已有研究成果表明，雙穩態系統中隨機共振現象可提高能量采集器回收的電能[7-9]。冷永剛等[10]建立了Duffing振子隨機共振的判別函數，闡述了Duffing振子在不同噪聲強度及信號頻率輸入條件下的廣義調參隨機共振規律。Zhang等[11]利用路面環境振動產生的噪聲激勵，成功地提高了懸臂梁的振動響應。Kim等[12]證明了旋轉系統中隨機共振頻率的可調節特性。然而，上述基于隨機共振的振動能量俘獲研究，只討論了在某一確定頻率下的隨機共振現象，盡管研究了可調節的隨機共振，但并未對其進行進一步的參數優化。

本文提出了一種基于自調節隨機共振的壓電式振動能量采集器模型(簡稱壓電懸臂梁)離心距優化方法。通過構建壓電懸臂梁動力學方程，結合自調節隨機共振優化離心距，與不可調節隨機共振和不同離心距下的壓電懸臂梁響應進行對比，結果表明基于自調節隨機共振優化后的離心距能更好地拓寬能量采集頻帶，提高能量俘獲性能，驗證了本文提出的離心距優化方法。

1 隨機共振的基本原理

雙穩態系統的動力學方程[13]為

(1)

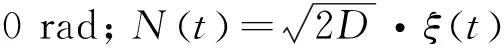
在無周期激勵時，系統勢函數在x=±(a/b)1/2處有2個對稱的最小值，勢阱高度ΔU=a2/(4)。在有周期激勵下，雙勢阱呈不對稱的上下傾斜，如圖1所示。

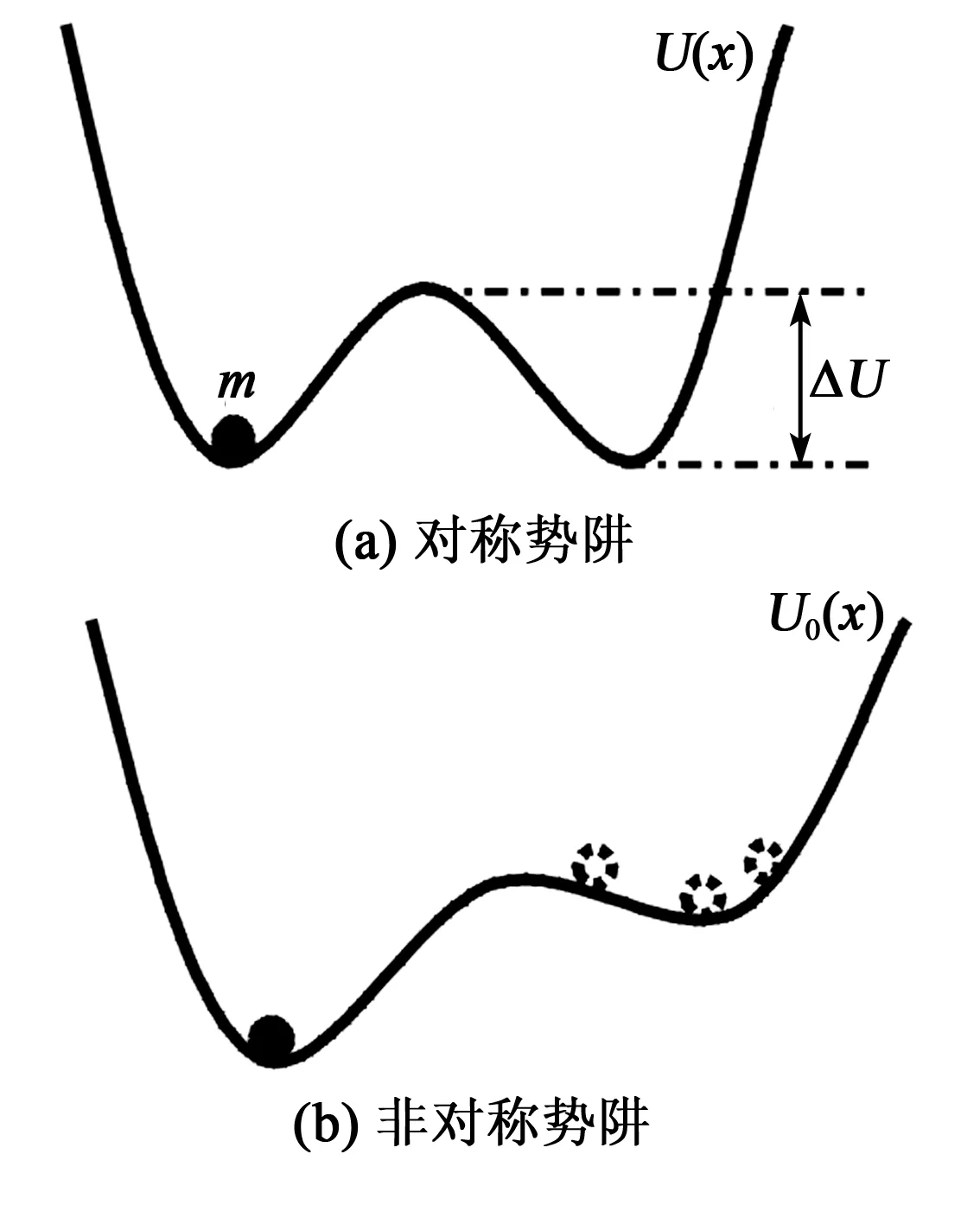
圖1 勢阱圖

標準勢能方程為

(2)

式(2)可轉化為

(3)

當周期激勵太弱不能使振子從某一勢阱躍遷至另一勢阱時，振子在某一勢阱內振蕩，而加入噪聲激勵后，振子獲得足夠的能量產生跳變，振子可在勢阱間振蕩。當振子阱間躍遷的平均等待時間Tw為周期激勵周期Ts的1/2時，振子躍遷與勢阱傾斜發生同步，即隨機共振的發生條件為

Ts=2Tw

(4)

用Kramers逃逸速率γk定義Tw=1/γk，其中γk[14]為

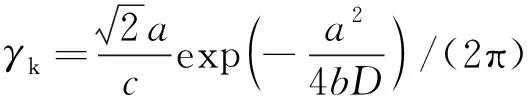
(5)

因此，由式(4)可知隨機共振頻率γ為

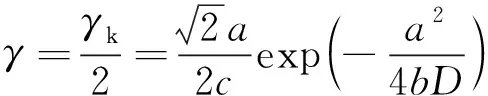
(6)

2 壓電懸臂梁的理論模型

本文將壓電懸臂梁安裝在輪胎上，噪聲激勵來自于不可預知的路面粗糙度，加上車輪引起的周期性旋轉力和磁體間的磁力，共同為隨機共振的發生提供了必要條件。

圖2為壓電懸臂梁模型示意圖。懸臂梁沿輪胎徑向安裝，包含2個磁鐵，一個位于懸臂梁的自由端，另一個固定安裝，其質量為m。壓電懸臂梁繞y軸旋轉，如果磁鐵間距d調至合適值，在磁鐵間的磁力FM的切向分量FH和懸臂梁恢復力kxT的共同作用下，懸臂梁末端磁鐵會在兩勢阱間來回振蕩，表現為雙穩態特征。

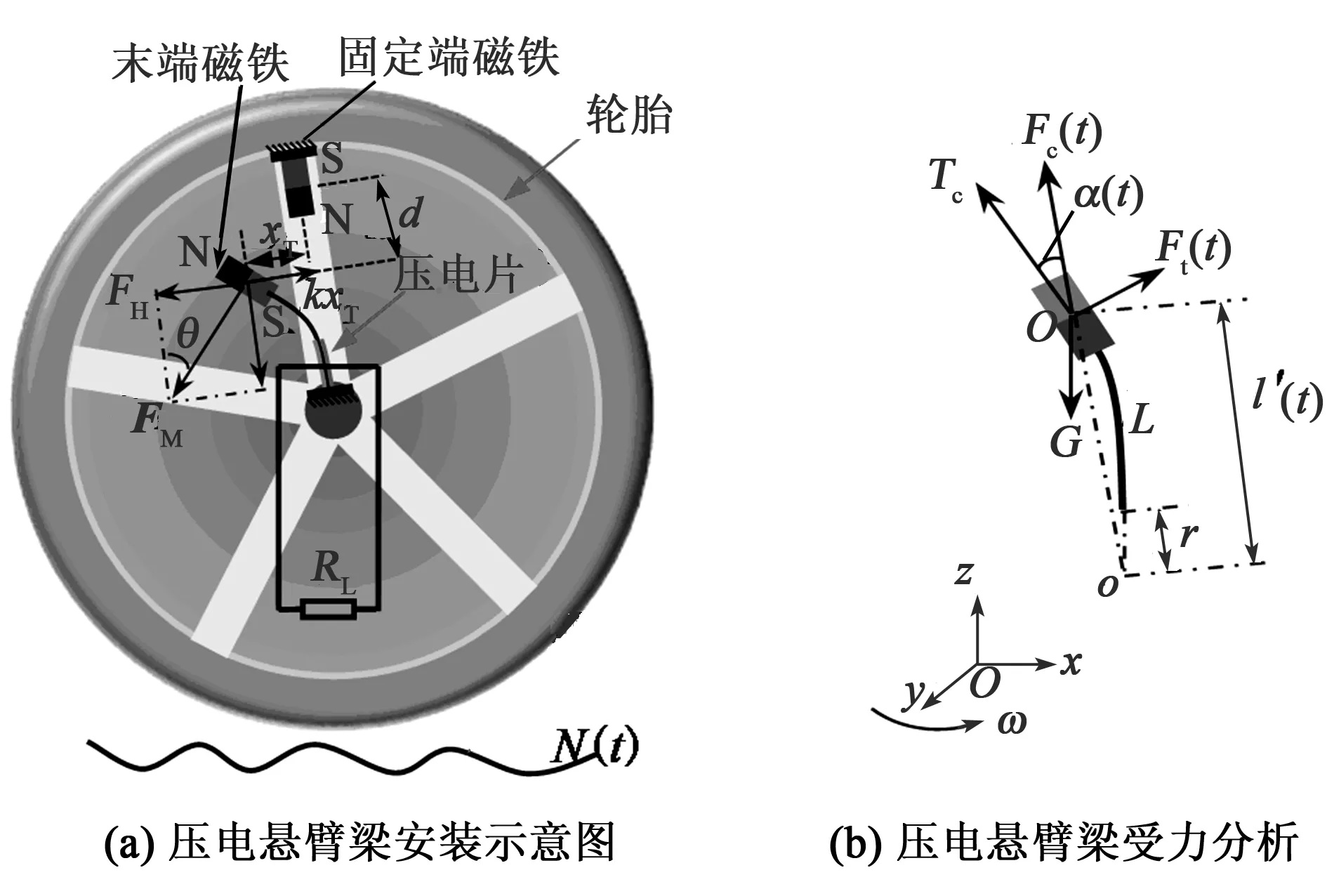
圖2 壓電懸臂梁模型示意圖

磁鐵間磁力切向分量FH可基于磁偶極子間的力學模型[15]：

FH=FMsinθ

(7)

式(7)在xT=0處進行泰勒展開并簡化為

(8)

式中:Mf=(Mfx,Mfy),Mc=(Mcx,Mcy)分別為懸臂梁末端磁鐵和固定端磁鐵磁化強度的水平分量和垂直分量；v為磁鐵體積；μ為真空中的磁導率；xT為末端磁鐵切向的位移。

由磁力產生的線性項和非線性項系數分別為

(9)

(10)

磁力切向分量FH可進一步表示為

(11)

當壓電懸臂梁以ω旋轉時，懸臂梁末端磁鐵離心力Fc(t)為

Fc(t)=mω2l′(t)

(12)

離心力切向分量為

Ft(t)=mω2l′(t)sinα(t)≈mω2l′(t)α(t)

(13)

式中：l′為末端磁鐵重心到旋轉中心的距離;α(t)為離心力Fc(t)與向心力Tc之間的夾角。

l′可表示為

(14)

式中：L為懸臂梁長度;r為懸臂梁根部到旋轉中心的距離。

懸臂梁的靜態偏轉為

(15)

式中：E為楊氏模量;I為慣性矩;xp為懸臂梁尖端位置到載荷力P′的距離。

懸臂梁尖端的偏轉角α(t)為

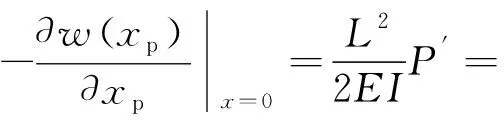
(16)

將式(14)、(16)代入式(13)可得離心力切向分量為

(17)

考慮離心力后的壓電懸臂梁的機械方程為

θpV+[G+N(t)]sinωt

(18)

式中：H=L+r為末端磁鐵的離心距(簡稱離心距)；k為懸臂梁剛度系數；V為負載端電壓；θp為機電耦合系數；Cp為壓電片的等效電容。

根據基爾霍夫定律，可得壓電懸臂梁的電學方程為

(19)

式中RL為負載阻抗。式(18)、(19)描述了壓電懸臂梁的振動能量俘獲機理。因此，壓電懸臂梁的等效剛度系數為

(20)

離心距H=0，即懸臂梁末端磁鐵位于輪胎旋轉中心時，磁鐵不受離心力作用，等效剛度為常數。當H≠0時，等效剛度隨旋轉頻率增加而增加，且不同離心距呈現不同的變化率，如圖3所示。

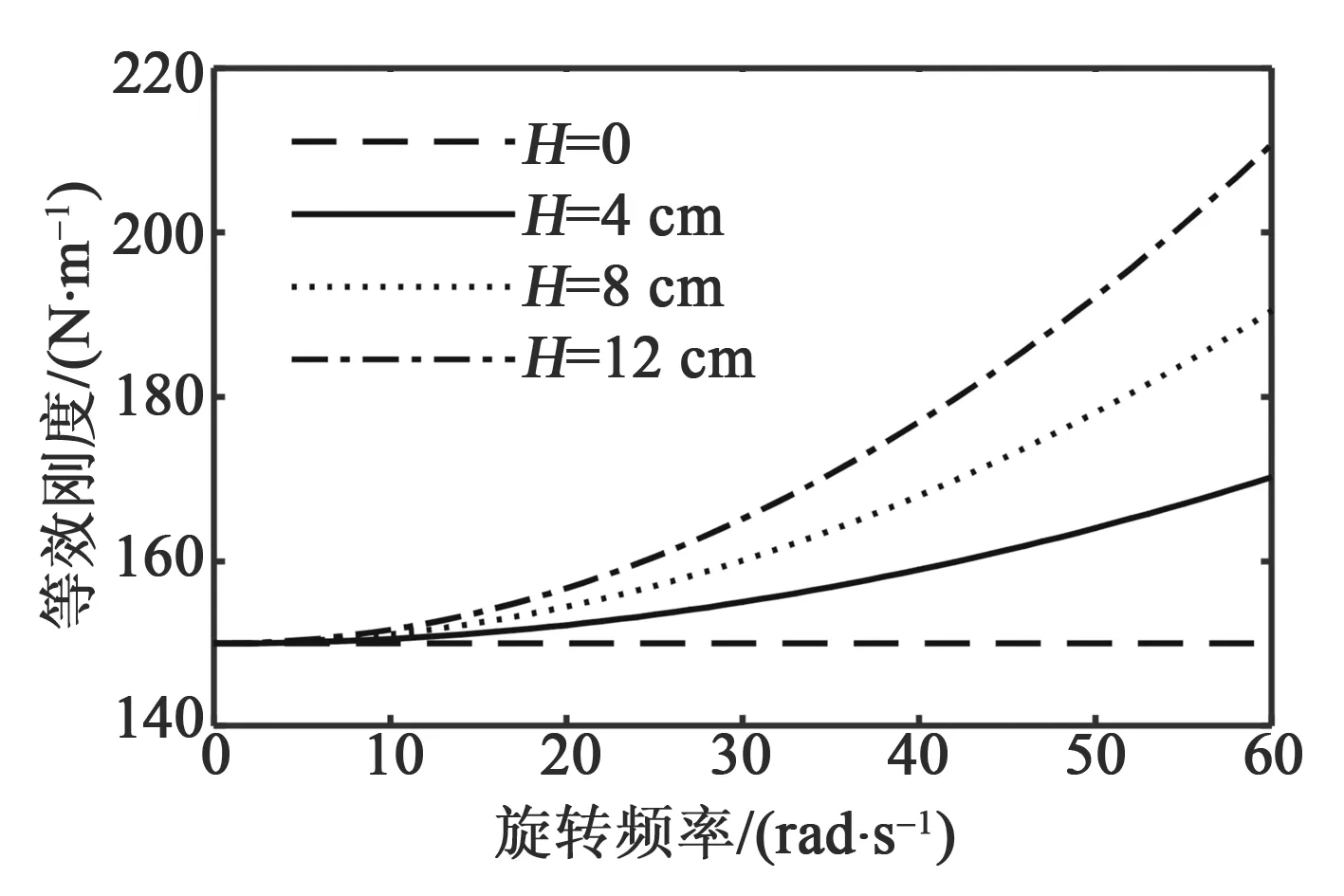
圖3 等效剛度系數

3 壓電懸臂梁在自調節隨機共振下的離心距優化

隨機共振的產生條件通常由Kramers逃逸速率定義。根據第2節的理論分析可知，伴隨旋轉頻率的變動，系統的線性項系數呈現可調節性變化趨勢。因此，隨機共振頻率同樣呈現可調節性變化趨勢即自調節隨機共振。旋轉環境下隨機共振頻率γ′可被進一步表示為

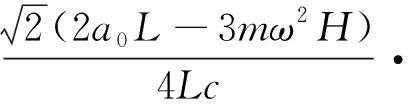
(21)

式中：a0=a′-k；c為阻尼系數。

為研究低頻區域的自調節隨機共振，通過分析式(21)可知存在最優離心距，在此離心距下，γ′(ω)與旋轉頻率能滿足較高的匹配。當滿足旋轉頻率等于γ′(ω)且與γ′(ω)相切時有

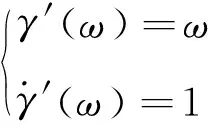
(22)

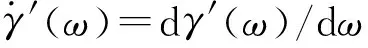
由式(22)可求出壓電懸臂梁最優離心距。根據γ′(ω)進一步可將式(22)表示為

(23)

令λ=ω2H，聯立式(22)中兩個條件式，可得關于λ的方程：

bD)λ-2a0bLD=0

(24)

由式(24)可得：

(25)

其中：

(26)

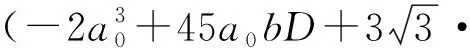
(27)

壓電懸臂梁的最優離心距與其對應的頻率點為

(28)

(29)

運用上述提出的壓電懸臂梁最優離心距優化方法，計算可得最優離心距。

選取雙穩態系統參數a0=75 N/m，b= 5.2×106N/m3，c= 0.25 N/(m·s-1)，D= 1.22×10-4N，不同離心距下隨機共振頻率曲線與旋轉頻率曲線的匹配結果，如圖4所示，當離心距為最優解 8ψL/(6a0-mψ)2/c2exp[-(6a0-mψ)2/(72bD)]時，求得離心距為6.45 cm，隨機共振頻率曲線與旋轉頻率曲線在30～60 rad/s內相切,且重合良好。

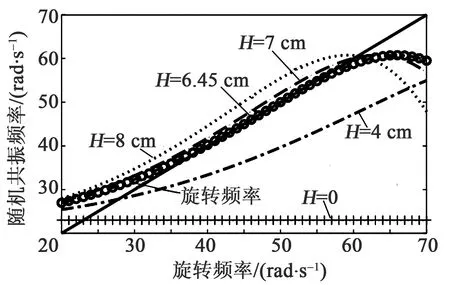
圖4 隨機共振頻率與旋轉頻率匹配圖

4 自調節隨機共振對壓電懸臂梁動態特性的影響

4.1 自調節與不可自調節隨機共振頻率的懸臂梁響應比較

本文在輪胎旋轉處于低頻區域(0～50 rad/s)環境下進行研究，當懸臂梁末端磁鐵重心位于旋轉中心即H=0時，磁鐵不受離心力作用，隨機共振頻率不可調節。H≠0時，末端磁鐵受離心力作用，懸臂梁等效剛度發生變化，隨機共振頻率可調節。壓電懸臂梁的速度和位移相軌跡如圖5所示。在低頻區域，不可自調節隨機共振的懸臂梁響應較差,如圖5(a)所示。自調節隨機共振的懸臂梁響應顯著提高，如圖5(b)所示。

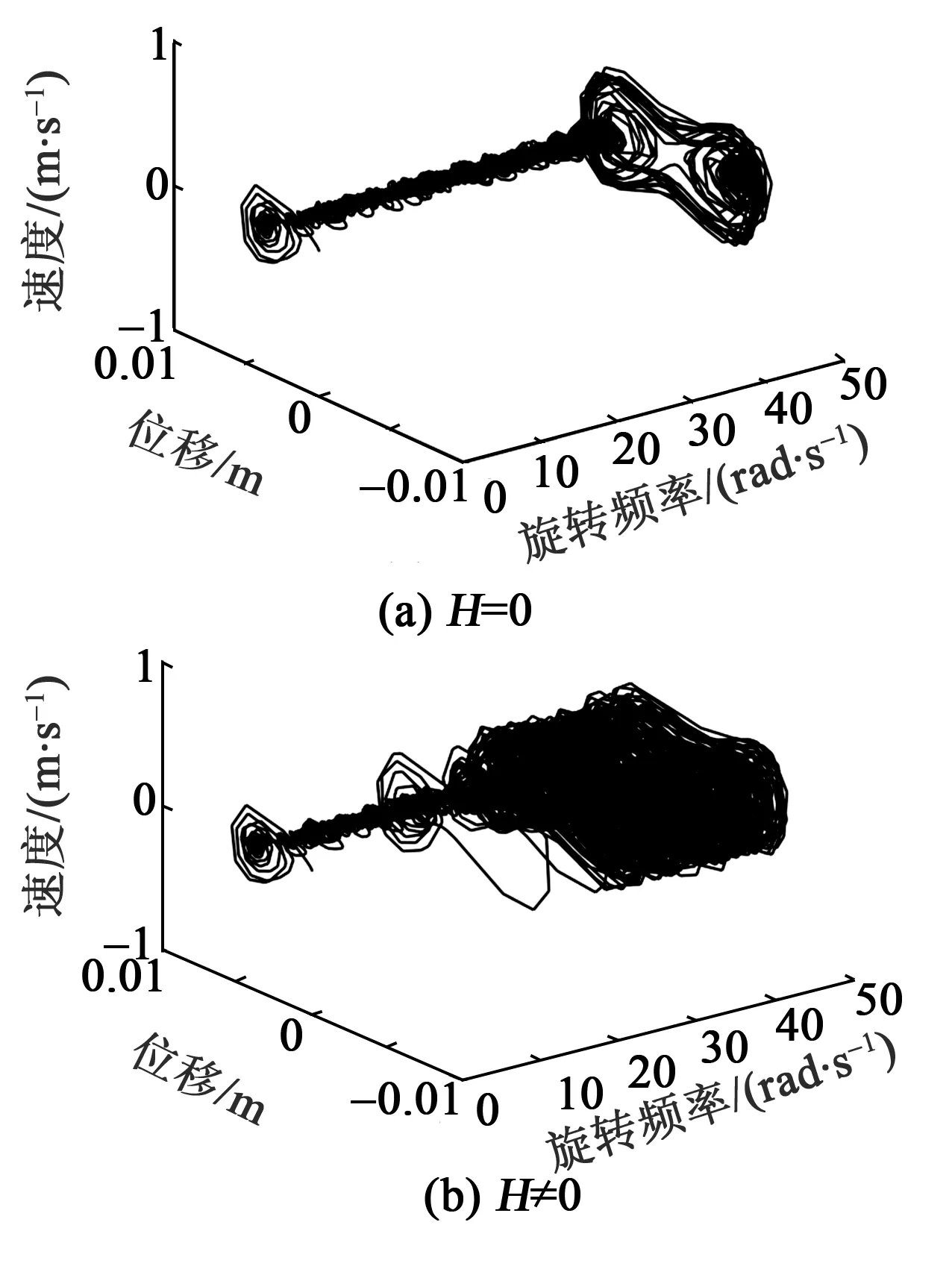
圖5 壓電懸臂梁的速度和位移相軌跡圖

4.2 離心距對壓電懸臂梁動態特性的影響

4.2.1 速度位移響應

本文所有數值模擬均在Matlab軟件中采用龍格-庫塔算法進行。壓電懸臂梁參數如表1所示。

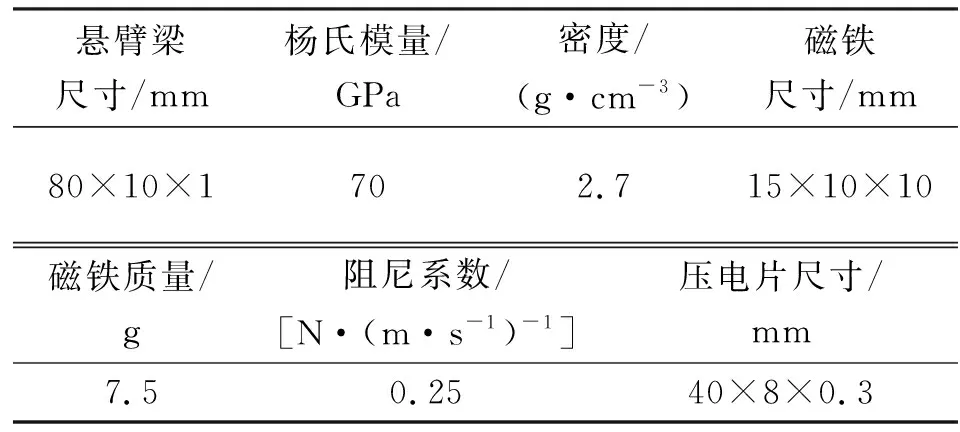
表1 壓電懸臂梁參數

考慮到離心距對壓電懸臂梁性能的影響，首先根據第3節的離心距優化法求出最優離心距H=6.45 cm，因此,離心距分別取0、4 cm、6.45 cm、7 cm、8 cm，分析壓電懸臂梁在低頻區域內的位移、分岔響應(圖中，灰色線為位移響應，黑色點劃線為分岔響應)和速度響應，如圖6、7所示。

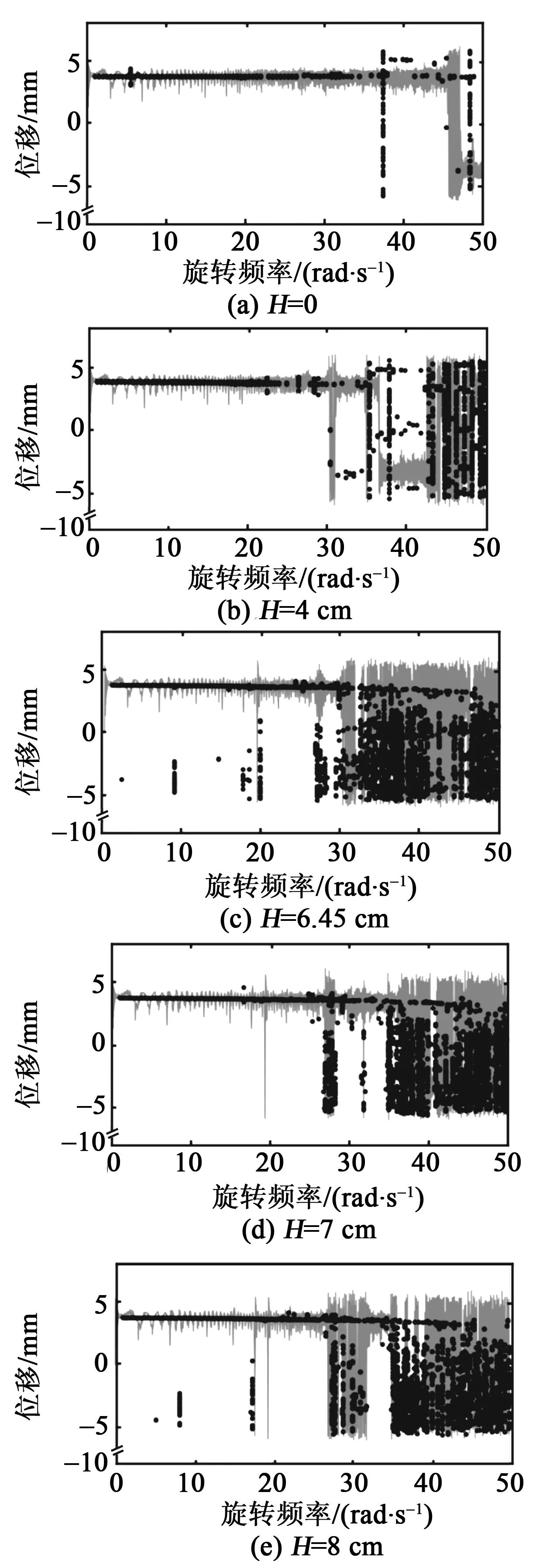
圖6 不同離心距下的位移和分岔響應

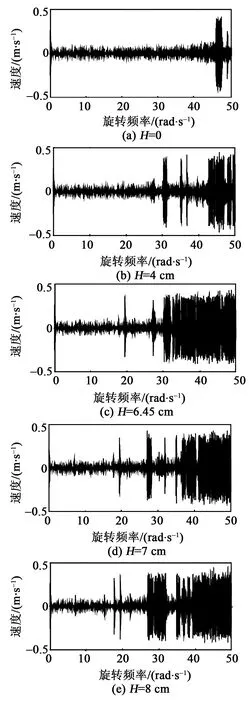
圖7 不同離心距下的速度響應

在0～50 rad/s，當H=0時，懸臂梁末端磁鐵在0～45 rad/s無足夠的動能躍過勢壘，做小幅低速運動，只在45～50 rad/s內偶爾跳出勢阱做大幅高速運動，隨機共振的影響較弱，整體動態響應較差。隨著離心距逐漸增大，當H=6.45 cm時，在自調節隨機共振的影響下，末端磁鐵在30～50 rad/s內有足夠的動能越過勢壘，做大幅高速運動且可保持相對持續穩定，整體動態響應提高。當H>6.45 cm時，末端磁鐵在30～40 rad/s 間盡管有自調節隨機共振的影響，但不能保持大幅高速運動。仿真結果表明，壓電懸臂梁在最優離心距條件下更易誘發并穩定隨機共振，擴展隨機共振的發生頻帶。

4.2.2 電壓響應

為了仿真不同離心距對壓電懸臂梁能量俘獲的影響，本文選取RL=33.4 kΩ，根據式(19)，仿真計算電阻兩端的電壓，計算結果如下：

1)H=6.45 cm為最優離心距時，此時壓電懸臂梁的瞬時電壓如圖8所示。

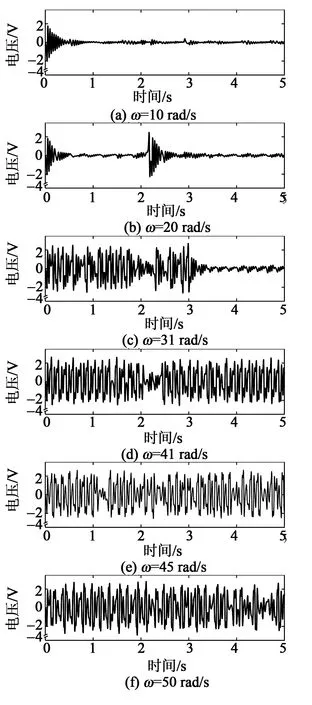
圖8 最優離心距時不同旋轉頻率的瞬時輸出電壓

2) 取H分別為0，4 cm，6.45 cm，7 cm，8 cm，此時壓電懸臂梁的電壓均方根值如圖9所示。

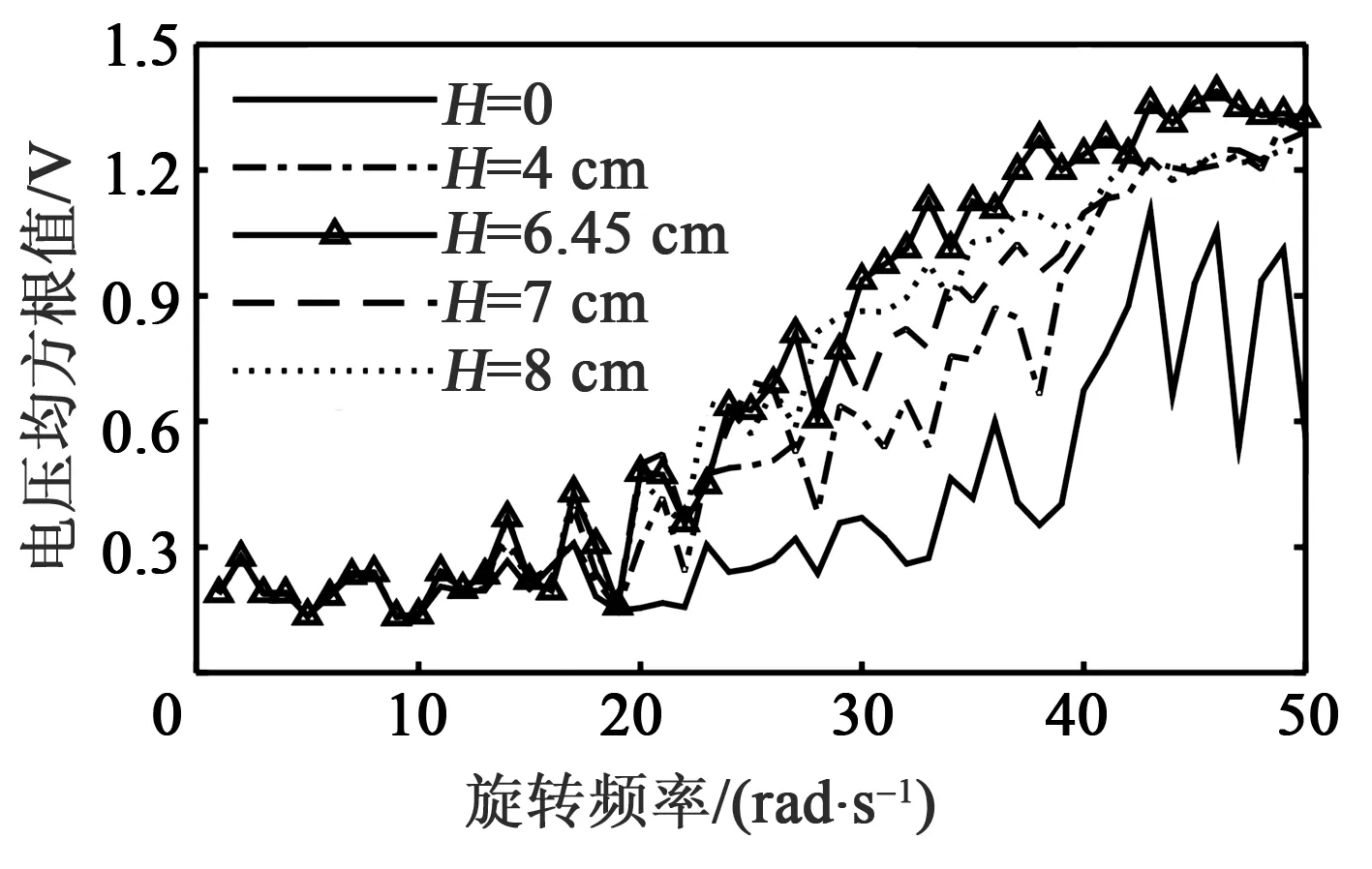
圖9 不同離心距下輸出電壓均方根值

圖9中每個點的數據為經過平均模擬時間100 s，固定旋轉頻率，每個離心距模擬40次后，計算出平均輸出電壓均方根值。設有效電壓為0.9 V，隨著離心距增加，電壓均方根值同時增加。當H=6.45 cm時，壓電懸臂梁的電壓均方根值在30～50 rad/s內達到最大值。隨著離心距繼續增大，電壓均方根值開始降低。由圖8可看出，在30～50 rad/s內電壓幅值顯著提高。上述分析結果與位移和速度響應分析結果相同。在30～50 rad/s，最優離心距(H=6.45 cm)下自調節隨機共振頻率使壓電懸臂梁的輸出電壓顯著提高，拓寬頻帶比約為40%，同時其輸出電壓高于其他離心距下的輸出電壓。

5 結論

本文建立了旋轉能量采集器的系統動力學模型，通過Kramers逃逸速率與旋轉頻率的非線性匹配關系，從理論上得到了最優離心距。對系統進行動力學特性仿真研究，得到不同離心距情況下采集器的響應情況，為壓電懸臂梁在低頻下的模型優化提供了一定的理論依據。研究表明：

1) 壓電懸臂梁安裝在輪胎上并處于旋轉狀態時，系統的等效剛度系數是關于旋轉頻率的函數，且系統的隨機共振頻率呈現可調特性。

2) 建立旋轉頻率與Kramers逃逸速率的優化匹配機制，可獲得最優離心距及其頻率匹配點理論模型。

3) 低頻區域自調節隨機共振在最優離心距條件下，更易誘發并穩定隨機共振，擴展隨機共振的發生頻帶，有效提高系統輸出響應，從而提升能量俘獲綜合性能，為自調節隨機共振在旋轉振動場景中的進一步廣泛應用提供了通用理論技術支撐。