操縱量對旋翼氣動噪聲的影響規律研究

李 騰, 曹亞雄, 李志彬，樊 楓

(中國直升機設計研究所，江西 景德鎮 333001)

0 引言

直升機獨特的垂直起降、空中懸停、回轉及超低空飛行能力，使其在軍事、民用領域均具有廣泛的用途，尤其在應對突發事件方面，更具有不可替代的作用。但是旋翼噪聲大的缺點，很大程度上限制了直升機更大范圍的使用。為降低旋翼產生的氣動噪聲，首先需要得到旋翼旋轉產生氣動噪聲的準確值。目前有試驗測量和基于FW-H方程的數值計算兩種方法可得到旋翼氣動噪聲。試驗測量直接采用麥克風采集聲信號。此方法可靠，且可與數值計算方法對比驗證數值計算準確性，但周期長、費時費力。數值計算例如采用WOPWOP聲預測代碼計算旋翼氣動噪聲，需要提供旋翼表面的氣動載荷以及旋翼操縱量作為輸入。旋翼表面的氣動載荷可通過風洞試驗測量或CFD(Computational Fluid Dynamics)計算得到。Visintainer把模型旋翼在DNW中試驗測得的表面壓力輸入到WOPWOP程序中預測噪聲，包括預測BVI噪聲。Hassan使用全位勢代碼預測旋翼在BVI狀態下的氣動載荷，并輸入到WOPWOP中，噪聲計算結果與試驗測得的噪聲值吻合一致。Kenneth介紹了槳葉運動及槳葉載荷簡化與否、總距、周期變距、預錐角和周期揮舞對旋翼聲預測的敏感性分析。操縱量變化對旋翼氣動噪聲大小及指向性的影響規律需要進一步研究。

本文的主要目的是了解當試驗測量或者數值計算旋翼產生的氣動噪聲時，旋翼操縱量對旋翼輻射噪聲的影響規律。文中旋翼氣動力采用Camrad II的自由尾跡模型進行計算；操縱狀態下旋翼產生的噪聲采用基于Farassat 1A方程進行氣動噪聲求解。采用2 m模型旋翼計算，針對斜下降典型槳渦干擾狀態，分析旋翼的不同操縱量對噪聲輻射的敏感性。

1 計算方法和模型

1.1 氣動力計算模型

如引言所述，文中采用Johnson創建的基于自由尾跡的Camrad II平臺進行旋翼的氣動計算。在自由尾跡方法中使用Weissinger-L模型，如圖1所示。此模型很好地結合了升力面方法和一階升力線的優點，也稱二階升力線方法。將尾跡分解為近尾跡和遠尾跡分別處理。近尾跡區域充分考慮附著渦和尾隨渦的影響，附著渦分布在網格四分之一弦線上，控制點分布在3/4弦線中點。附著渦環量徑向變化引起尾隨渦從槳葉后緣拖出，設置渦齡角為30°后形成近尾跡。遠尾跡區域主要由自由運動的卷起槳尖渦來模擬，考慮槳尖渦誘導作用，渦元誘導速度由Biot-Savart(B-S)定律確定，如式(1)所示。考慮到槳尖渦附近誘導速度計算存在奇異性，采用渦核模型對槳尖渦進行模擬，如式(2)所示。

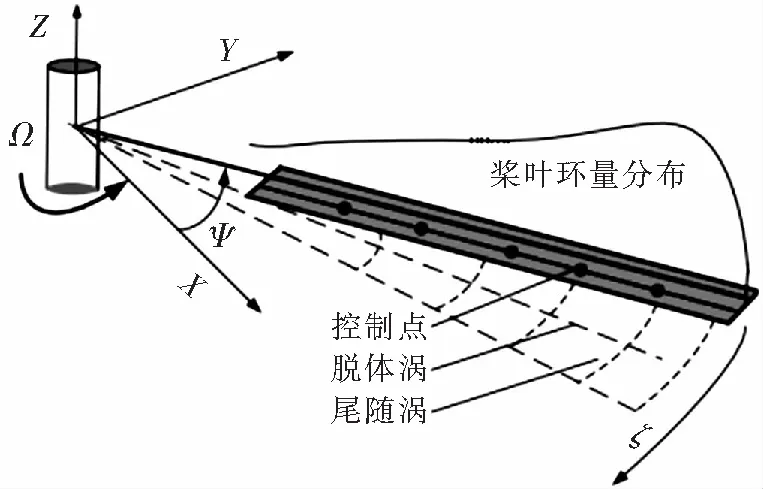
圖1 槳葉Weissing-L升力面示意圖

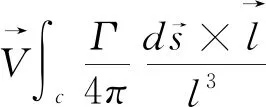
(1)

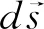
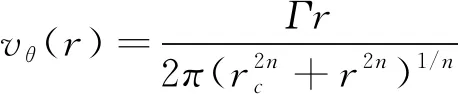
(2)

式中，為計算點至渦中心的距離，為渦核半徑。渦核半徑定義為最大切向速度出現的位置。

1.2 噪聲計算模型

在旋翼氣動噪聲計算方面，Ffowcs Williams-Hawkings在Lighthill方程的基礎上運用廣義函數理論創建了固體邊界氣動發聲的FW-H方程。當旋翼槳尖馬赫數為亞音速時，四極子噪聲對總噪聲的貢獻很小，可以忽略不計。FW-H方程忽略四極子噪聲項后使用最廣泛的形式是Farassat推導出的積分形式的F1A公式，如下所示：

(,)=(,)+(，)

(3)

式中,(，) 為總聲壓,(，)是厚度噪聲聲壓，(，)為載荷噪聲聲壓，二者的表達式分別為：

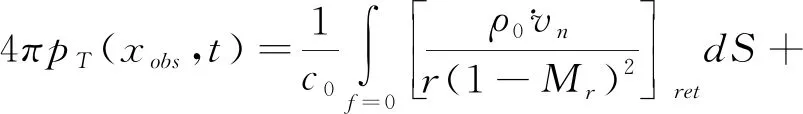
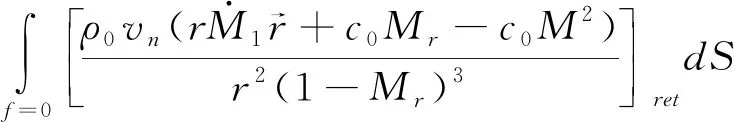
(4)

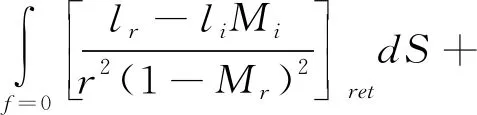
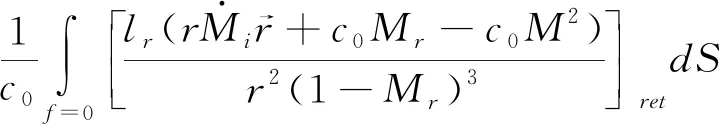
(5)

2 方法驗證

為檢驗本文噪聲計算方法對直升機旋翼前飛狀態氣動噪聲的計算能力，選取AH-1/OLS模型旋翼作為驗證算例。Schmitz等人測量了AH-1/OLS模型旋翼多個狀態下的噪聲數據，選取“10014狀態”進行噪聲計算來驗證文中建立的計算方法。OLS旋翼是AH-1直升機旋翼的 1/7 縮比模型。旋翼的參數為：2片槳葉， BHT-540對稱翼型，直徑1.916 m，弦長0.104 m，展弦比9.22，槳葉根切比18.2%，-10°的線性扭轉。槳盤傾角為1°，旋翼流場中存在明顯的槳-渦干擾(BVI)現象。AH-1G/OLS模型旋翼如圖2所示。

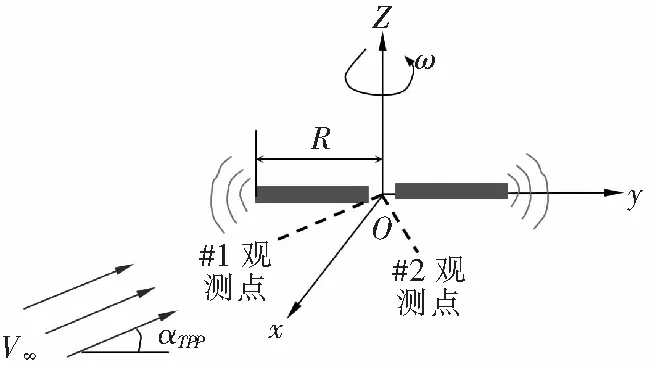
圖2 AH-1G/OLS模型旋翼示意圖

從圖3中可以看出，本文方法在相位和幅值上均能較為準確地計算出AH-1/OLS旋翼在該狀態下45°方位角左右的聲壓正峰值，這也正是槳-渦干擾狀態的典型特征，表明了本文所建立的方法具有計算旋翼槳-渦干擾狀態氣動性能和噪聲特性的能力。

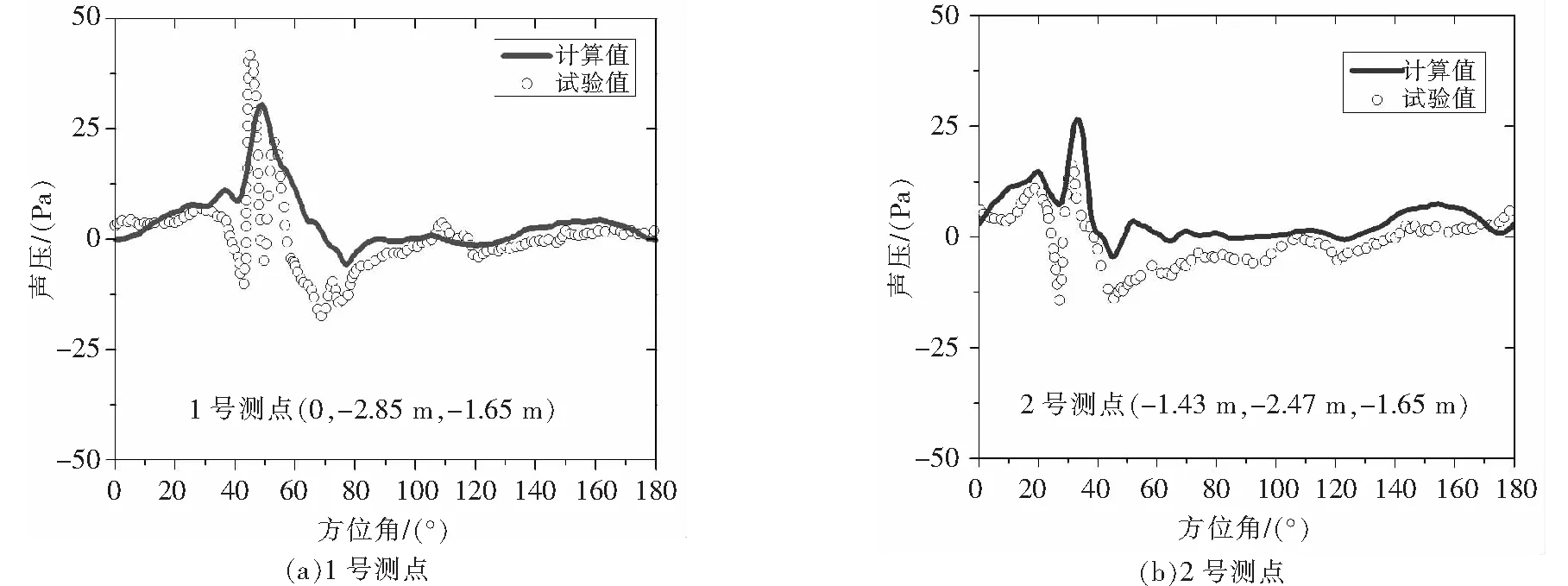
圖3 AH-1G/OLS旋翼在典型槳-渦干擾狀態下的噪聲計算對比

3 操縱量對旋翼噪聲敏感性分析

3.1 計算模型

采用2 m模型旋翼，旋翼幾何信息如表1所示。

表1 模型槳葉幾何信息

懸停狀態槳盤一周同一俯仰角對應的各個方位角處觀測點的聲壓級都相同，所以結果處理只選擇某一方位角處不同俯角處觀測點的聲壓級即可。文中觀測點位于0°方位角處，俯角以10°增加，具體編號如圖4所示。懸停按照機身重量133 kg配平，配平變量為“向力”和“總距”，配平后錐度角=197°，總距為=964°，設此狀態為基準狀態。基準狀態下各個觀測點聲壓級噪聲如圖5所示。圖中可知#3觀測點聲壓級最高。根據旋翼產生的不同成分噪聲的傳播方向，選擇#1，#3，#5觀測點。保證槳葉氣動載荷計算準確的前提下，分析旋翼各操縱量變化對旋翼噪聲的影響。

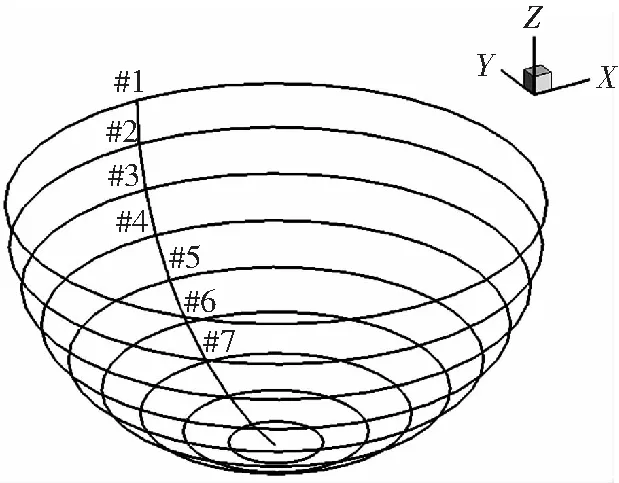
圖4 觀測點位置

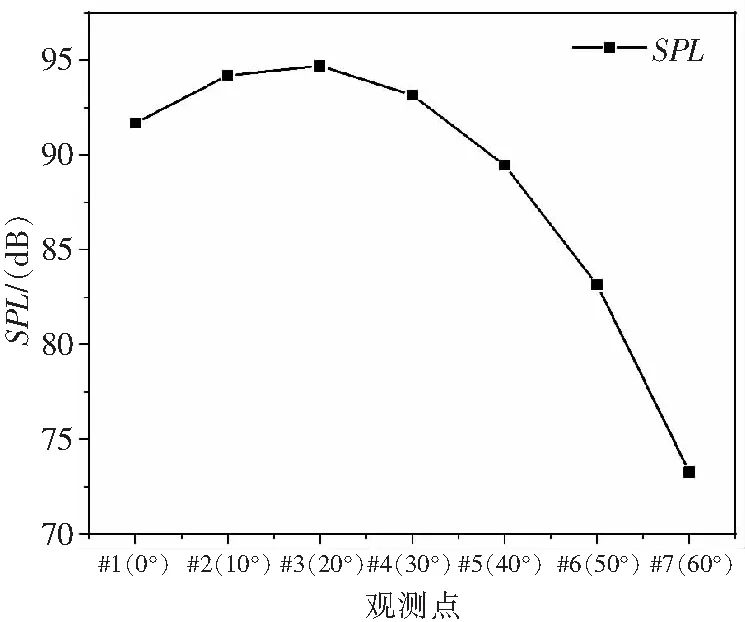
圖5 基準狀態下各觀測點聲壓級

3.2 懸停狀態參數影響分析

3.2.1 錐度角影響

圖6和表2給出了懸停狀態下錐度角變化對旋翼噪聲的影響。錐度角的變化為=0°、1°、1.97°、3°、4°，Δ=-1.97°、Δ=-1.97°、-0.97°、0°、1.03°、2.03°。可以看出錐度角變化對各觀測點厚度噪聲幾乎沒有影響，這與已知厚度噪聲僅由旋翼幾何特性決定的結論相吻合。錐度角變化對槳盤平面內觀測點處(#1)載荷噪聲的影響要大于對槳盤下方觀測點處(#3、#5)載荷噪聲的影響。因此，需要考慮錐度角變化對槳盤平面內觀測點噪聲的影響；對槳盤平面下方其他觀測點而言可以忽略錐度角對噪聲的影響。

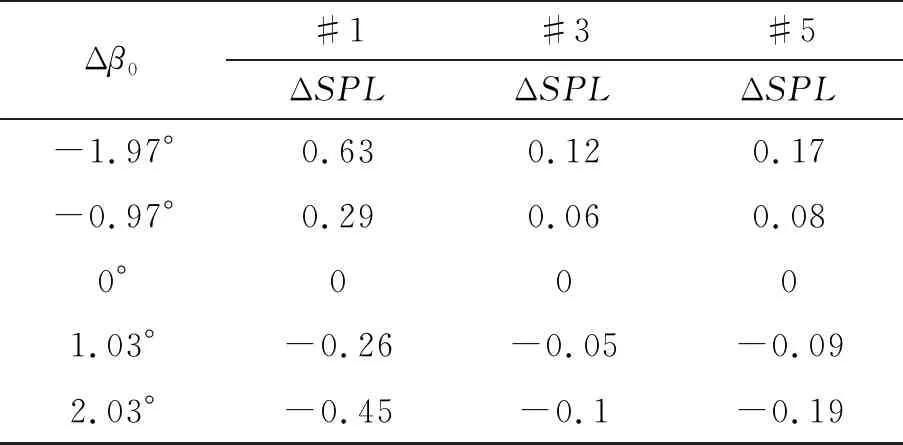
表2 錐度角變化對各觀測點聲壓級的影響

圖6 懸停狀態錐度角影響

3.2.2 總距角影響

圖7和表3給出了懸停狀態下，旋翼總距角變化對3個觀測點處聲壓級的影響。=7.5°、8.5°、9.64°、10.5°、11.5°，定義Δ=-9.64°，Δ=-2.14°、-1.14°、0°、0.86°、1.86°。同樣可以看出總距變化對各觀測點厚度噪聲幾乎沒有影響，僅對載荷噪聲產生影響。總距角增大，各個觀測點處載荷噪聲均增大。

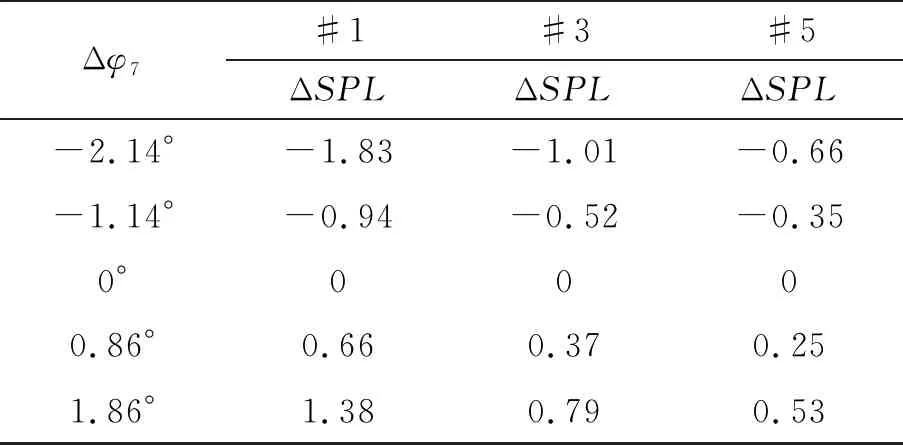
表3 總距變化對各觀測點處聲壓級的影響

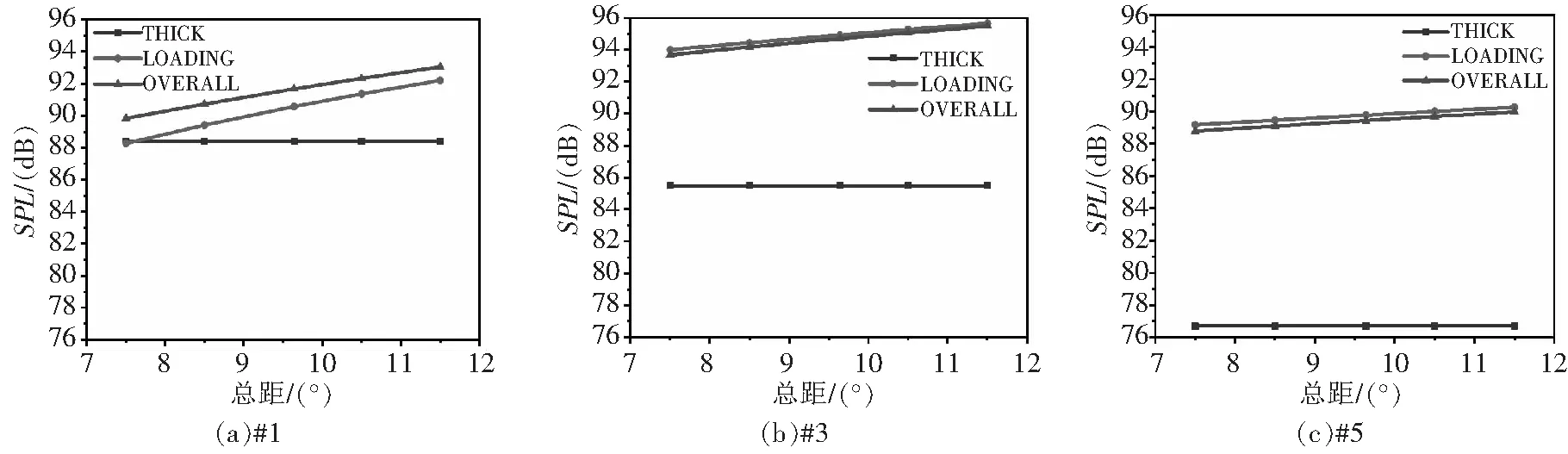
圖7 懸停狀態總距變化對各觀測點噪聲的影響

3.3 前飛狀態參數影響分析

前進比=0.15，配平后旋翼的操縱量如表4所示。圖8為前飛狀態下旋翼的聲輻射球，設此狀態為基準狀態。

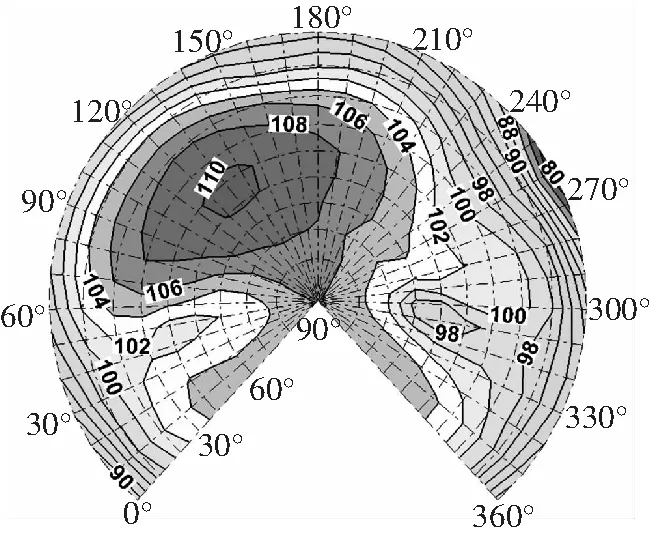
圖8 前飛基準狀態聲輻射球

表4 前飛基準狀態旋翼配平后的操縱量

3.3.1 軸傾角的影響

采用單一變量法，保證其他參數不變，改變軸傾角。=-1°，-2°，-3°,Δ=-(-253°),故Δ=153°,053°,-148°。圖9為不同軸傾角狀態下對應的聲輻射球。圖9(a)中可以看出軸傾角增量為1.53°時，10°方位角槳盤平面聲壓級減小2.4 dB； 方位角160°處槳盤平面內及下方5°范圍內噪聲減小1.8 dB；而150°～180°方位角，槳盤下方10°范圍內噪聲增大1.4 dB。對比圖9(a)、(b)、(c)可知，前飛時，軸傾角的變化會影響10°方位角和槳盤前方觀測區域處的噪聲，軸傾角前傾越大，噪聲差值越大，軸傾角變化小時(0.5°)，可忽略軸傾角的影響。

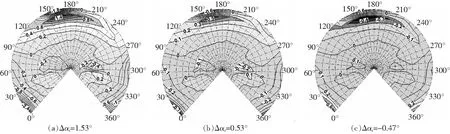
圖9 前飛狀態軸傾角的影響

3.3.2 錐度角的影響

其他參數不變，錐度角的變化為=1°,2°，Δ=-045°,055°。圖10(a)中250°方位角處槳盤平面內噪聲增大0.9 dB，而270°方位角處噪聲減小0.3 dB。對比圖10(a)、(b)兩圖可發現，錐度角減小或增大后，對應的噪聲增大和減小區域剛好對調。錐度角的變化較小時，對觀測點噪聲的影響不明顯，可忽略錐度角的影響。

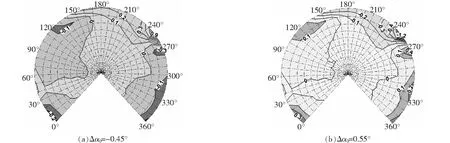
圖10 前飛狀態錐度角的影響

3.3.3 后倒角和側倒角的影響

圖11為1和1同時為0°和2°旋翼的聲輻射球，以此來分析后倒和側倒的影響。圖11(a)可以看出后倒和側倒角變化較小(1=1=0°)時，260°方位角處槳盤平面內噪聲增大0.7 dB，其他觀測點噪聲影響不大，可以忽略對旋翼噪聲的影響；圖11(b)中當后倒和側倒角變化較大時(1=1=2°)，方位角240°～300°范圍內噪聲增大1 dB，最大值可達4 dB，其他區域噪聲噪聲影響不大。所以，后倒角和側倒角變化小時，可以忽略其影響。

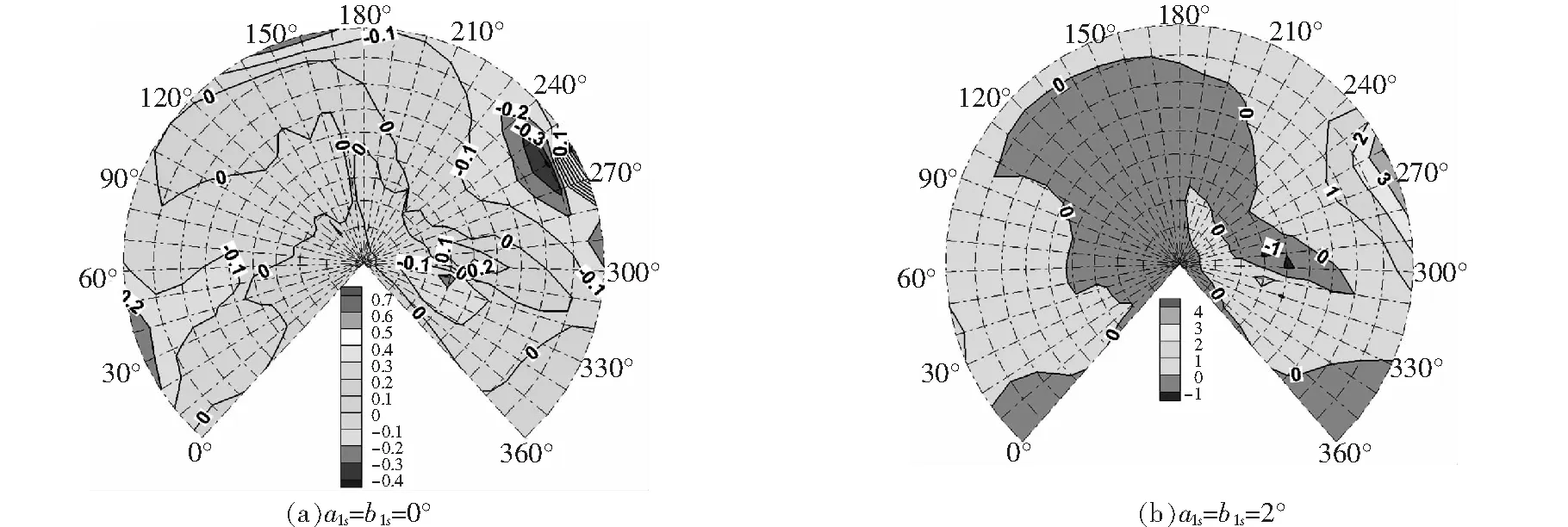
圖11 前飛狀態下后倒角和側倒角的影響

3.3.4 周期變距的影響

其他參數不變，橫向周期變距的變化為=-1°，-3°,Δ=077°,-123°。對比圖12(a)、(b)可發現，橫向周期變距增大或者減小，聲輻射球噪聲降低區域和增大區域正好對調；橫向周期變距變化，影響的是20°～50°方位角、240°附近和270°附近觀測點的噪聲。對比圖8基準狀態可知，橫向周期變距的變化對噪聲指向性無影響。

圖12 前飛狀態橫向周期變距的影響

圖13為縱向周期變距變化后旋翼產生噪聲的變化。=1°,3°,4°，Δ=-127°,073°173°。可以看出，縱向周期變距影響的是槳盤后方0°～30°方位角、槳盤前下方150°～180°方位角和210°～330°后行側范圍靠近槳盤平面的區域，且縱向周期變距變化幅值增大，噪聲變化幅值增大，影響越大，但對噪聲指向性并不構成影響。

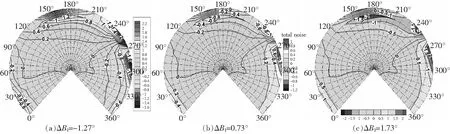
圖13 前飛狀態縱向周期變距的影響

3.4 斜下降參數影響分析

接著分析斜下降狀態操縱量對旋翼噪聲的影響。軌跡角為-6°，前進比0.15，配平后旋翼的操縱量如表5所示。圖14為前飛狀態下旋翼的聲輻射球，設為基準狀態。

表5 斜下降狀態配平后旋翼的操縱量

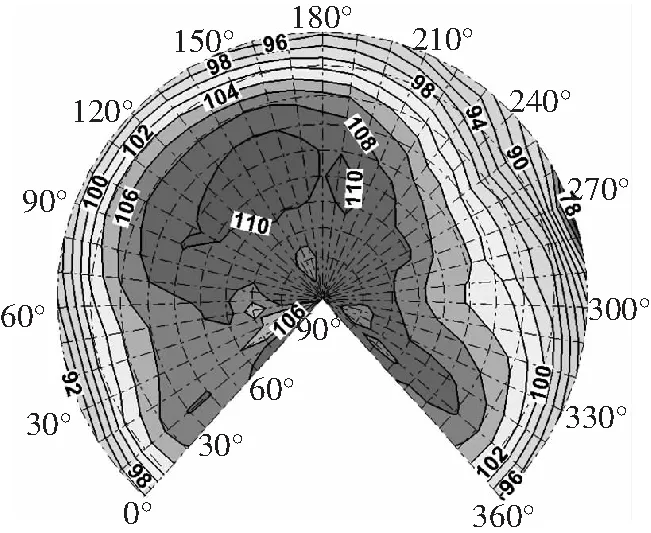
圖14 斜下降基準狀態聲輻射球

3.4.1 軸傾角的影響

其他參數不變，軸傾角變化為=-1°,-3°，Δ=092°,-108°。圖15中可以看出斜下降狀態軸傾角變化對旋翼噪聲的影響同前飛狀態下軸傾角變化對旋翼噪聲的影響相似。軸前傾越大(=-108°)，旋翼前下方10°～20°俯角范圍噪聲降低1 dB，槳盤下方5°范圍內噪聲增大1.2 dB；槳盤20°方位角后方增加1.2 dB。軸前傾角相對基準狀態變小(=092°)，噪聲變化區域正好對調。軸傾角變化1°幅值左右，對噪聲的影響大約為1 dB。

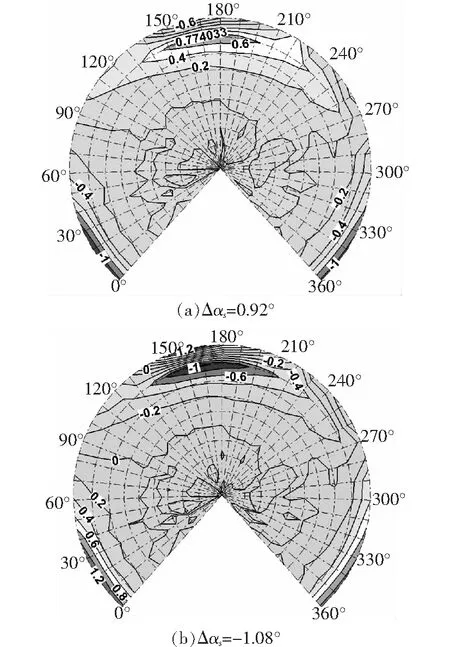
圖15 斜下降狀態軸傾角的影響

3.4.2 錐度角的影響

其他參數不變，錐度角的變化為=1°,2°，Δ=-03575°,06425°。圖16斜下降情況下錐度角的影響同前飛狀態相似。錐度角變化會影響250°和270°方位角附近觀測點的噪聲，但對噪聲指向性并不構成影響。

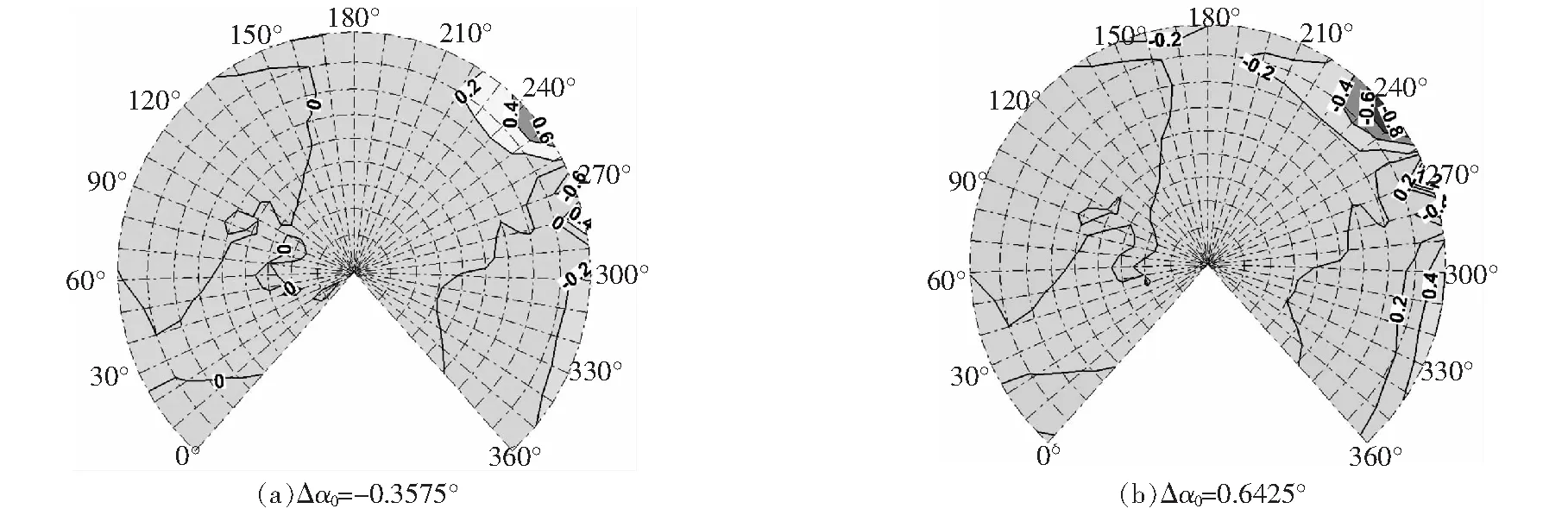
圖16 斜下降狀態錐度角的影響

343 后倒角和側倒角的影響

同樣設置1和1同時為0°和2°，分析后倒和側倒的影響，如圖17所示。忽略后倒側倒(1=1=0°)，260°方位角、槳盤下方15°觀測點附近，噪聲降低0.6 dB，270°方位角噪聲增大1.2 dB；后倒角和側倒角增大，后行側240°～310°范圍內噪聲增大1 dB以上。因此，后倒角和側倒角變化小時，可以忽略影響。

圖17 斜下降狀態后倒角和側倒角的影響

3.4.4 周期變距的影響

其他參數不變，橫向周期變距的變化為=-1°,-3°,Δ=087°,-113°。對比圖18(a)、(b)可發現，橫向周期增大和減小，聲輻射球噪聲降低區域和增大區域正好對調；橫向周期變距變化，影響的是前行側20°～150°方位角、250°附近和280°附近后行側觀測點的噪聲。對比圖14基準狀態可知，橫向周期變距的變化對噪聲指向性無影響。

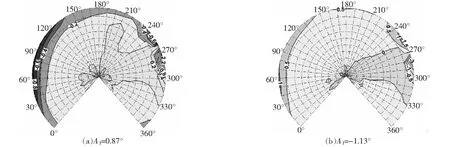
圖18 斜下降狀態橫向周期變距的影響

其他參數不變，縱向周期變距的變化為=05°,1°,3°,4°，Δ=-125°,-074°,126°,226°。從圖19可以看出縱向周期變距影響的是槳盤后方0°～40°方位角、槳盤前下方150°～180°方位角和260°～360°后行側范圍靠近槳盤平面的區域，且縱向周期變距變化幅值增大，噪聲變化幅值增大，影響增大，但對噪聲指向性并不構成影響。

圖19 斜下降狀態縱向周期變距的影響

3.5 爬升參數影響分析

爬升狀態，配平后旋翼的操縱量如表6所示。圖 20為爬升狀態下旋翼的聲輻射球，設為基準狀態。

表6 爬升狀態配平后旋翼的操縱量

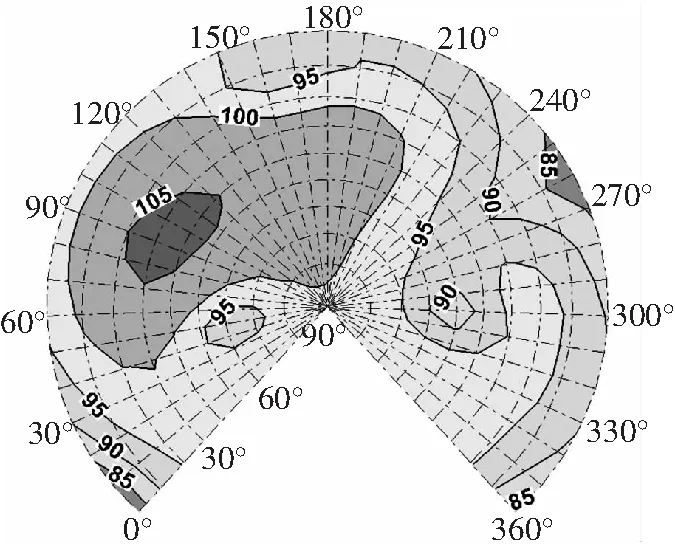
圖20 爬升狀態基準狀態下的聲輻射球

351 軸傾角的影響

其他參數不變，軸傾角變化為--1°,-3°，Δ=129°,-171°。軸前傾增大(=-171°)，旋翼前下方噪聲降低0.6 dB，后方增加1 dB。軸前傾角相對基準狀態變小(=129°)，噪聲變化區域正好對調，旋翼前下方噪聲增大1.2 dB，正后方噪聲減小2.2 dB。

3.5.2 錐度角的影響

其他參數不變，錐度角的變化為=05°,25°,Δ=-10141°,09859° 。圖22爬升情況下錐度角的影響同前飛狀態相似。錐度角變化會影響10°和240°方位角附近觀測點的噪聲，但對噪聲指向性并不構成影響。

3.5.3 后倒角和側倒角的影響

設置1和1同時為0°和2°，分析后倒和側倒的影響，如圖23所示。忽略后倒、側倒(1=1=0°)，260°方位角、槳盤下方10°觀測點附近，噪聲增大0.9 dB，20°方位角噪聲減小0.4 dB；后倒角和側倒角增大(1=1=2°)，后行側240°～270°范圍內噪聲減小1 dB以上，10°～50°方位角噪聲增加1 dB以上，270°下方20°方位角附近噪聲增大1.5 dB。所以后倒角和側倒角變化小時，可以忽略其影響。

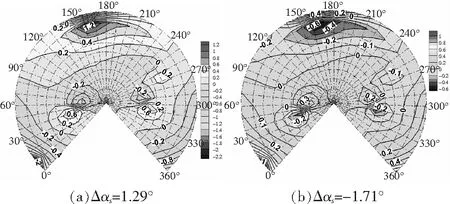
圖21 爬升狀態軸傾角的影響

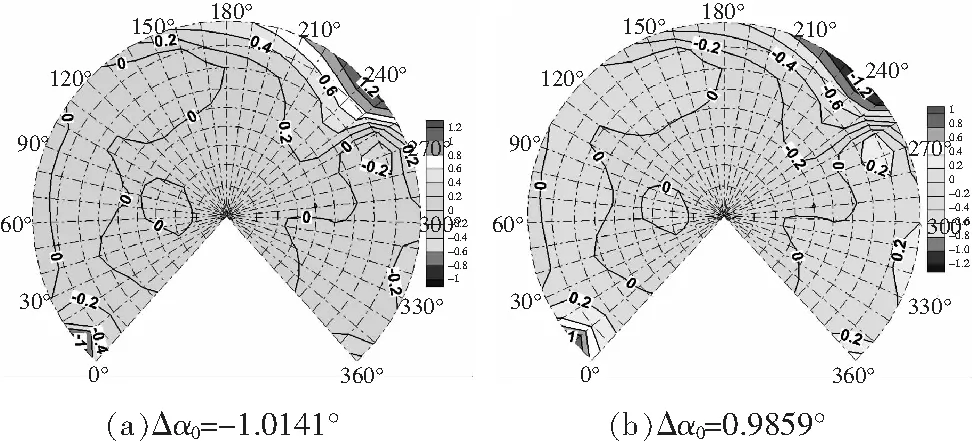
圖22 爬升狀態錐度角的影響

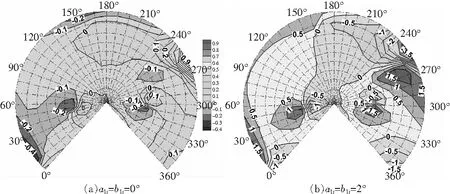
圖23 爬升狀態后倒角和側倒角的影響

3.5.4 周期變距的影響

其他參數不變，橫向周期變距的變化為=-05°,-2°，-3°Δ=089°,-061,-061°。同樣對比圖24(a)、(b)、(c)可發現，橫向周期增大或減小，聲輻射球噪聲降低區域和增大區域正好對調；橫向周期變距變化，影響的是0°～30°方位角、260°附近觀測點的噪聲，且周期變化幅值相對于基準值增大，噪聲影響區域擴大。對比圖20基準狀態可知，橫向周期變距的變化對噪聲指向性無影響。

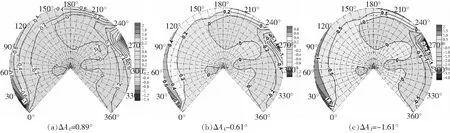
圖24 爬升狀態橫向周期變距的影響

其他參數不變，縱向周期變距的變化為=1°,2°,3°,4°，Δ=-141°,-041°,059°,159°。可以看出縱向周期變距影響的是槳盤后方0°～60°方位角、槳盤前下方150°～180°方位角和210°～330°后行側范圍靠近槳盤平面的區域，且縱向周期變距變化幅值增大，噪聲變化幅值增大，影響增大，但對噪聲指向性并不構成影響。

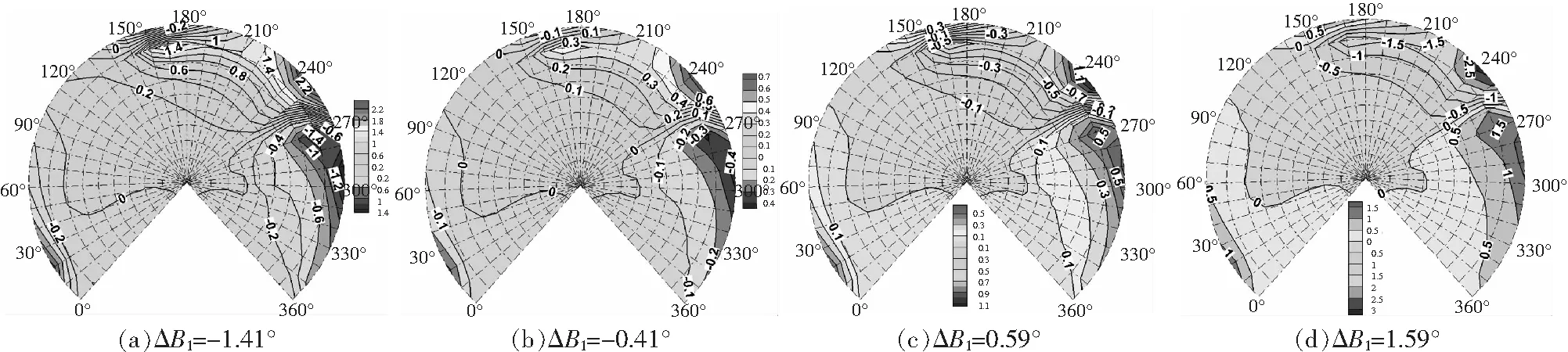
圖25 爬升狀態縱向周期變距的影響

4 結論

本文基于自由尾跡模型和Farassat 1A方程對旋翼在不同操縱量下的噪聲進行計算研究，得出的結論如下：

1)懸停時，錐度角變化對槳盤平面內觀測點處載荷噪聲的影響最大，只需考慮其變化對槳盤平面內觀測點噪聲的影響，忽略對槳盤平面下方的影響；總距角增大，對所有觀測點處載荷噪聲和厚度噪聲的影響均增大，但變化量小時增量并不大。

2)前飛時、斜下降和爬升狀態下，各操縱量變化對旋翼噪聲的影響規律相似。操縱量的改變不會對噪聲指向性產生影響。

3)軸傾角的變化會影響槳盤后方和槳盤前方方位角處下方20°范圍內觀測區域的噪聲，且軸傾角前傾越大，對噪聲的影響越大，軸傾角變化小于0.5°，可忽略軸傾角的影響；錐度角的影響可忽略不計。

4)揮舞一階對噪聲的影響也集中在槳盤平面附近，變化較小時同樣可忽略其影響；一階周期變距影響后行側，且變化越大，影響范圍越廣，噪聲變化值越大。