朱文慶，仲唯貴

(中國直升機設計研究所，江西 景德鎮(zhèn) 333001)

0 引言

直升機在大速度前飛時包含了大量的類圓柱流動，例如起落架的輪子、支柱，槳轂雷達，主減塔座，排氣管等。這些部件自身的氣流分離和尾跡及其與下游部件的干涉形成明顯的振動，如直升機中常見的尾篩現(xiàn)象就是由主減塔座、尾氣管等上游脫落渦與垂尾干涉形成的。起落架中的類圓柱流動還會形成顯著的噪聲輻射，如大型的商用固定翼飛機中，降落狀態(tài)時起落架噪聲占總噪聲的比重達40%。大型直升機也具有較大尺寸的起落架，如米-26主起落架直徑達1.12 m，在大速度前飛時，起落架也會產生顯著的振動和噪聲。事實上，直升機起落架的噪聲已得到相關學者的關注。

阻尼網作為流動控制裝置已在風洞中得到廣泛的應用，近年來，其噪聲控制效果也得到了大量的試驗試飛的驗證。歐盟和日本均啟動了飛行試驗項目來驗證阻尼網的降噪效果。在歐盟的SILENCE(Significantly Lower Community Exposure to Aircraft Noise)項目中，使用阻尼網代替整流罩以減弱對附近流體的加速和轉向，降低了起落架的感受性噪聲1.8 dB。日本的FQUROH(Flight demonstration of QUiet technology to Reduce nOise from High-lift configurations)項目中，通過飛行試驗驗證了阻尼網降噪的有效性，在90°輻射方向上，總聲壓級降低為4.2～4.4 dB。

實際上，航空器中的部件外形復雜，不利于機理層面的研究。為此，相關學者以圓柱、工字梁等簡化模型為對象，開展了阻尼網對噪聲的控制研究。Boorsma等以單圓柱和工字梁為研究對象，探索了不同開孔率的阻尼網對噪聲的影響規(guī)律。Oerlemans等研究了阻尼網幾何參數(shù)對降噪的影響，橫向的橢圓形阻尼網具有最好的降噪效果，能降低中低頻噪聲25 dB，使之到達背景噪聲的水平。

為研究更多的流動細節(jié)，增進對阻尼網控制流動和噪聲的理解，近年來，對阻尼網的數(shù)值模擬研究不斷涌現(xiàn)。Murayama等對安裝阻尼網的主起落架進行了數(shù)值模擬，計算中解析了阻尼網的幾何外形。在FQUROH項目中，Murayama等又對“Hisho”驗證機的主起落架進行了數(shù)值模擬，計算重現(xiàn)了風洞試驗和飛行試驗中的控制結果，但計算網格量達到了2.5億左右。

阻尼網復雜多尺度的外形對直接解析方法造成了巨大的挑戰(zhàn)。為提高計算效率，Okolo等在流場中阻尼網所在位置設置虛擬區(qū)域，在該區(qū)域上添加體積力源項來代替阻尼網的作用，但并未對模化方法和流場改變做詳細描述，也缺乏嚴謹?shù)尿炞C工作和機理探討。朱文慶等對該方法做了進一步的發(fā)展和驗證。

本文的主要目的是采用阻尼網數(shù)值模型研究阻尼網在圓柱繞流中對流動和噪聲的控制機理和控制規(guī)律，為阻尼網在直升機流動控制中的應用奠定理論基礎。

1 數(shù)值方法

1.1 阻尼網模型

本文采用由朱文慶等開發(fā)的數(shù)值模型。在該模型中，阻尼網對流動的影響分為4項：流動阻力，速度折射，對來流湍流的衰減和自身湍流的產生。本文的阻尼網放置在圓柱之前，不需要考慮對來流湍流的衰減；阻尼網自身產生的湍流具有非常小的尺度，在本文中可以忽略。故本文的阻尼網模型只考慮流動阻力和速度折射。

1.1.1 流動阻力

本文的阻尼網主要應用于直升機中，此時飛行馬赫數(shù)≈ 0.2。阻尼網的絲線直徑在毫米量級。例如，在TIMPAN項目中6個阻尼網的絲線直徑在0.1～1.19 mm之間；基于絲線直徑的雷諾數(shù)范圍為400～5000。考慮雷諾數(shù)范圍，選用Roach公式：

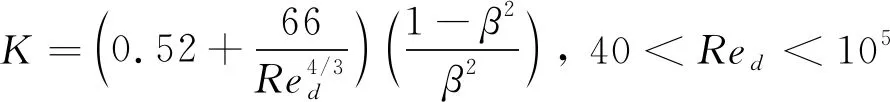
(1)

1.1.2 速度折射

根據(jù)已有的文獻分析，速度折射依賴于阻力系數(shù)和入射角度。TIMPAN項目中用于大量測試的開孔率范圍為053～060。根據(jù)Boorsma等控制鈍體噪聲的經驗，在入射角度較小時，對流動和噪聲的控制效果大；當> 45°時，再增加穿孔區(qū)域的面積，對噪聲無明顯影響。

基于阻尼網的使用工況，選用Gibbing的經驗公式：

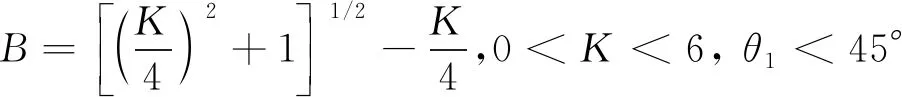
(2)

阻尼網模型要求在阻尼網區(qū)域內添加源項來代替阻尼網對流場的作用，如圖1所示。

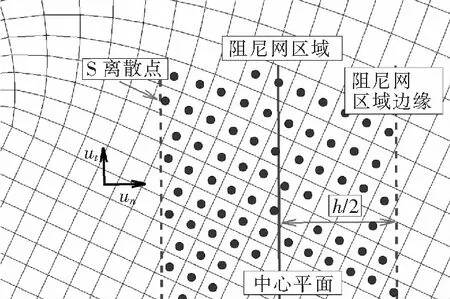
圖1 阻尼網實現(xiàn)方式示意圖

在阻尼網區(qū)域，積分形式的N-S方程寫為：

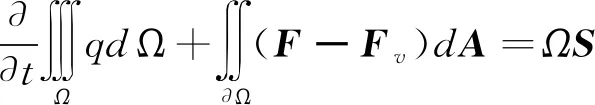
(3)

阻尼網的影響以體積力的形式包含在中：

=[0·]

(4)

為推導的具體形式，此處引入阻尼網當?shù)氐姆ㄏ騿挝皇噶浚瑢⒌竭_阻尼網的速度分為法向速度和切向速度：

=(·)

=-

(5)

體積力可表示為：

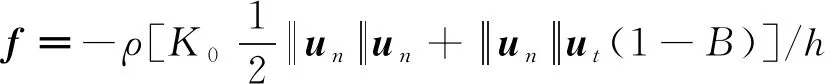
(6)

其中代表阻尼網區(qū)域的厚度。在本文中以×代替參與計算，是為了數(shù)值穩(wěn)定性而添加的分布函數(shù)，它具有如下形式：

()=2(1-2)

(7)

其中代表距離阻尼網區(qū)域中心平面的法向距離。分布函數(shù)使得源項更集中在阻尼網區(qū)域的中心，有利于降低離散誤差，同時也能減小阻尼網區(qū)域的有效厚度。

1.2 其他數(shù)值方法

本文使用IDDES(Improved Delayed Detach Eddy Simulation)計算聲源場的湍流流動。該方法有效結合了帶壁面模型的LES和DDES方法的優(yōu)點，能改善壁面湍流的模擬。計算中無粘通量采用四階中心和Roe格式的混合格式，并引入自適應耗散函數(shù)以降低湍流區(qū)的格式耗散。界面通量采用5階WENO格式重構。粘性通量采用二階中心格式。在時間推進上，采用帶牛頓子迭代LU-SGS方法，能實現(xiàn)二階計算精度。

使用可穿透的FW-H方程計算噪聲的傳播。在噪聲求解上采用預先時間步方法，即基于聲源時間計算接收點的時間，然后用最大二階的插值方式將聲壓插值到接收點的時間離散點上。該方法能使流場計算和噪聲計算同步進行，避免了大量的聲源數(shù)據(jù)的存儲。

2 阻尼網模型的驗證

本文采用防風柵算例對阻尼網模型進行驗證。該防風柵在外形上與阻尼網極為相似，其試驗和計算設置如圖2所示。試驗中防風柵的高度=100 mm，寬高比為3。該防風柵由3 mm寬的方木條裝訂而成，木條間距10 mm，開孔率= 0.49，基于木條寬度的雷諾數(shù)為1830。

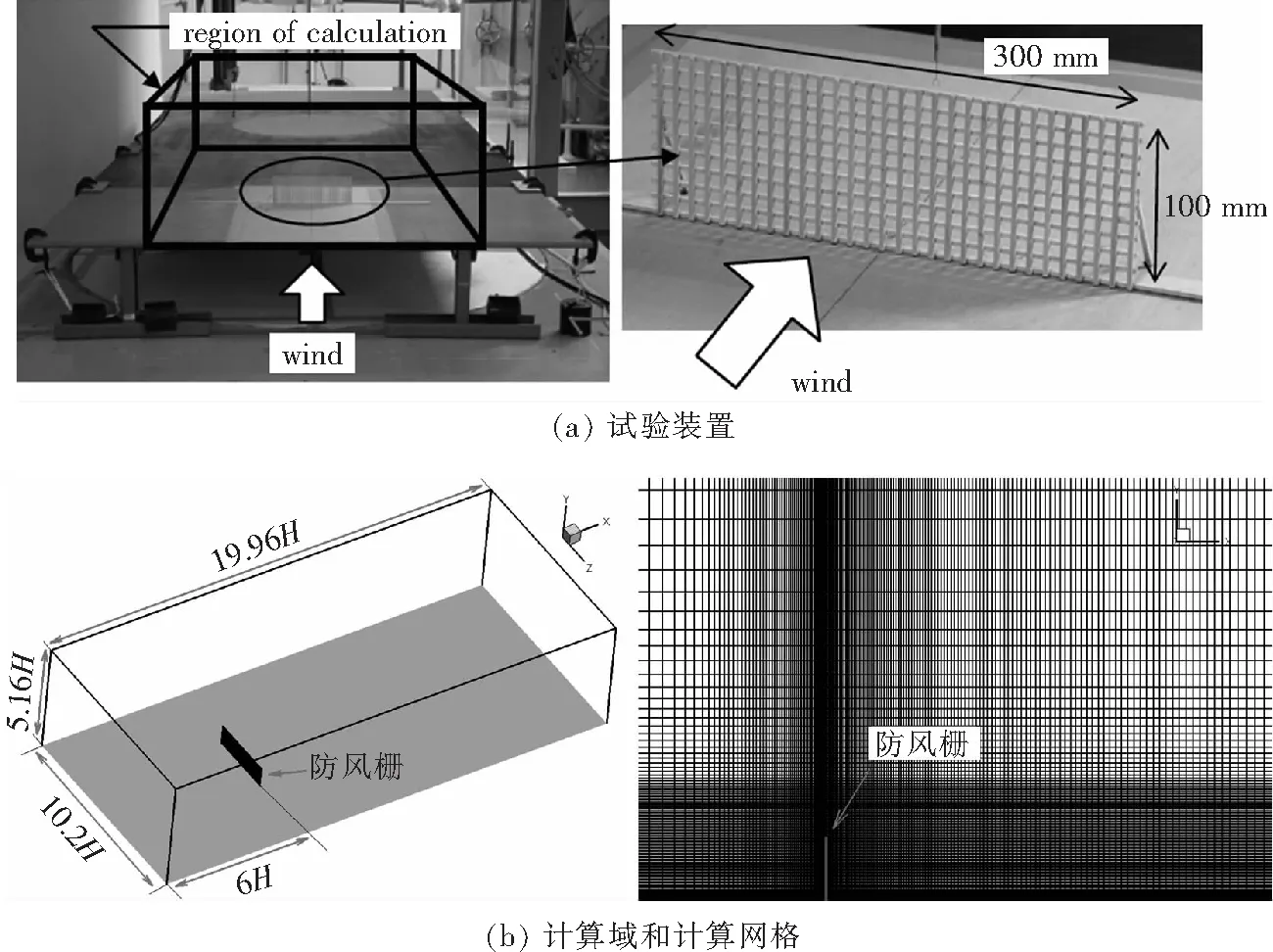
圖2 試驗和計算設置示意圖

計算中來流馬赫數(shù)為0.1，計算區(qū)域與試驗相同，從防風柵上游6到下游1396，高度方向為516，展向寬度為102。在防風柵區(qū)域，網格尺度為002，總網格量約為65 × 106。本算例中網格不足以解析壁面湍流，故采用定常RANS方法進行計算。本文計算了042和049兩個開孔率，以探究開孔率對流場的影響。

圖3給出了開孔率為049時平均速度的分布，阻尼網提供了流動的阻力，在其后形成了低速區(qū)域。圖4則給出了流向和法向速度型與試驗的定量對比。開孔率為049時，防風柵前(= -1)和后(= 1,2,4)的速度型與試驗值在趨勢上相符，但在幅值上存在一定的差距。當開孔率增加到042時，幅值與試驗相符。

圖3 展向和垂向截面中平均速度的分布(β=0.49)

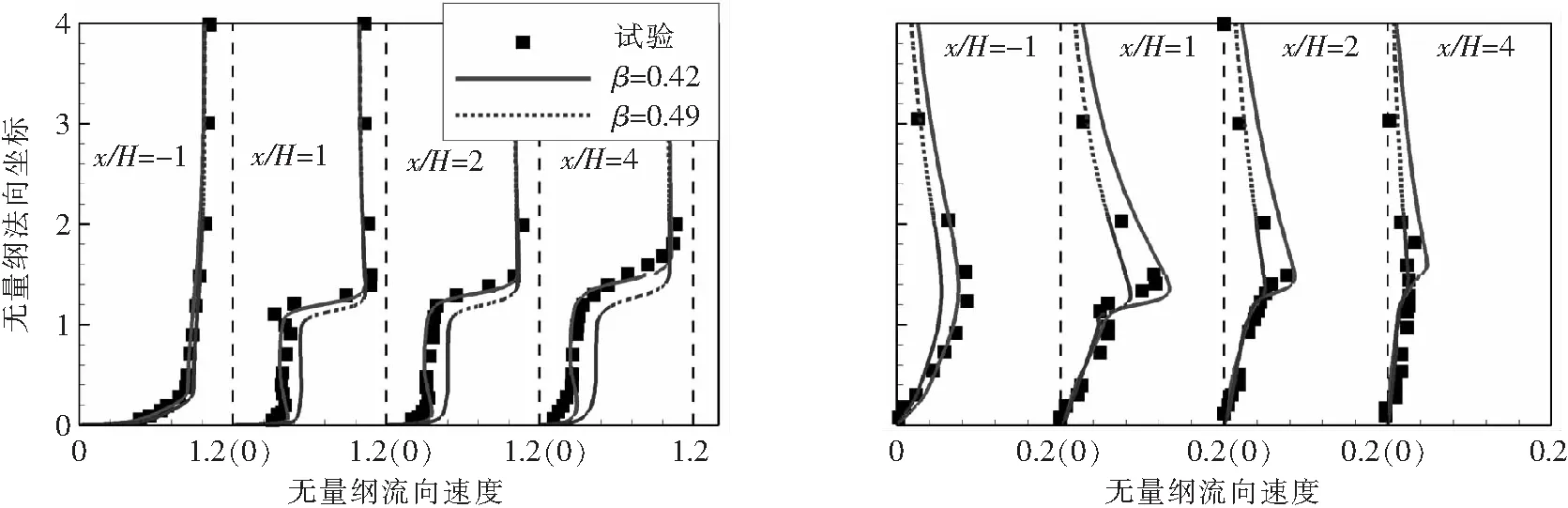
圖4 流向和法向速度型與試驗的對比

該算例中合適的阻力系數(shù)能夠得到與試驗相符的速度分布，進一步證明了本文計算方法的可靠性。

3 阻尼網控制圓柱的流動和噪聲

本文的研究對象為Boorsma等的試驗中的單圓柱，直徑=100 mm，展向長度=514。試驗中使用穿孔板控制圓柱噪聲，所使用穿孔板和其安裝位置如圖5所示。穿孔板直徑= 150 mm，穿孔板的厚度為2 mm。該穿孔板只在部分區(qū)域開孔，開孔區(qū)域的環(huán)向范圍為[-45°, 45°]，前駐點角度為0。本文研究在穿孔區(qū)域使用阻尼網對圓柱流動和噪聲的控制效果。

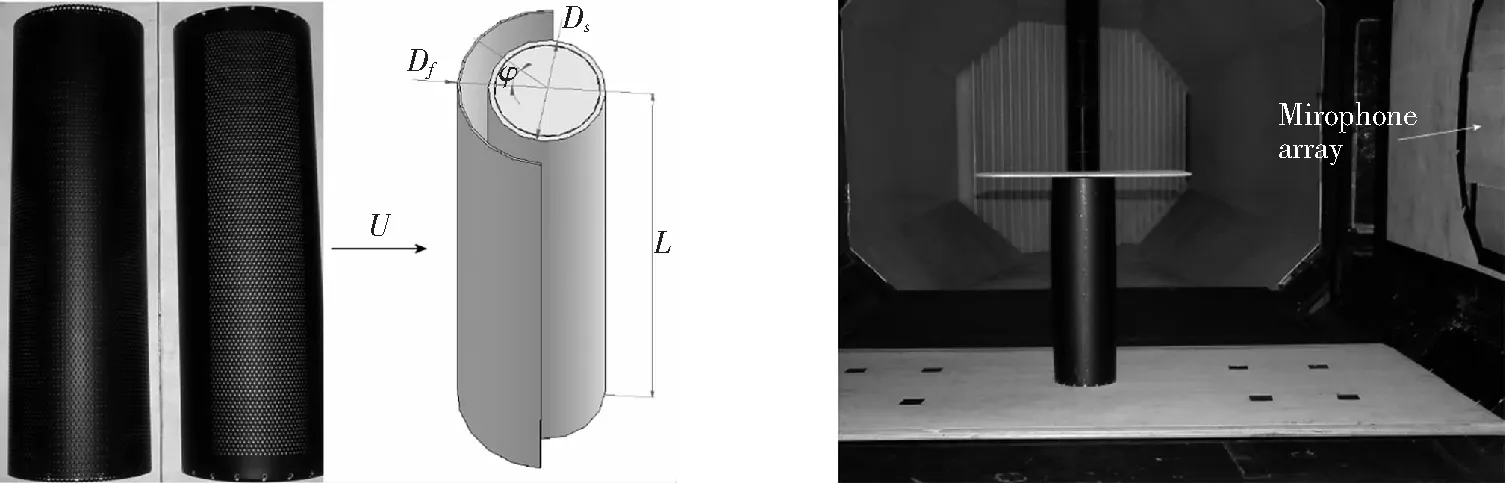
圖5 穿孔板及其安裝位置示意圖[7]

計算中來流=0.2，基于圓柱直徑的雷諾數(shù)= 2.6×10。圓柱表面和整流罩非開孔區(qū)域采用無滑移壁面條件，阻尼網區(qū)域采用本文的阻尼網模型。

圖6對比了單圓柱，阻尼網開孔率0.42和0.55三個算例的Q等值面。在安裝阻尼網的算例中，一部分流體能穿過開孔區(qū)域，流向單圓柱；一部分流體將繞過整流罩。整流罩內外的速度差在其尾部形成剪切層。單圓柱和阻尼網開孔率0.42時表現(xiàn)出明顯的渦脫特性：單圓柱的渦脫是由其本身的分離渦脫落產生；阻尼網開孔率為0.42時，渦脫則表現(xiàn)為整流罩的分離渦脫落。當開孔率增加到0.55時，不再觀察到渦脫現(xiàn)象。

圖6 不同算例的Q等值面對比

圖7為平均流場的對比，同時也包含了Boorsma等試驗中穿孔板開孔率為0.42時的結果。阻尼網增大了圓柱后的分離區(qū)，單圓柱尾跡區(qū)的再附點位置為1.78，開孔率為042和055時的再附點位置分別為316和41。此外，開孔率為042時，本文計算和Boorsma等的試驗具有相似的分離形態(tài)。

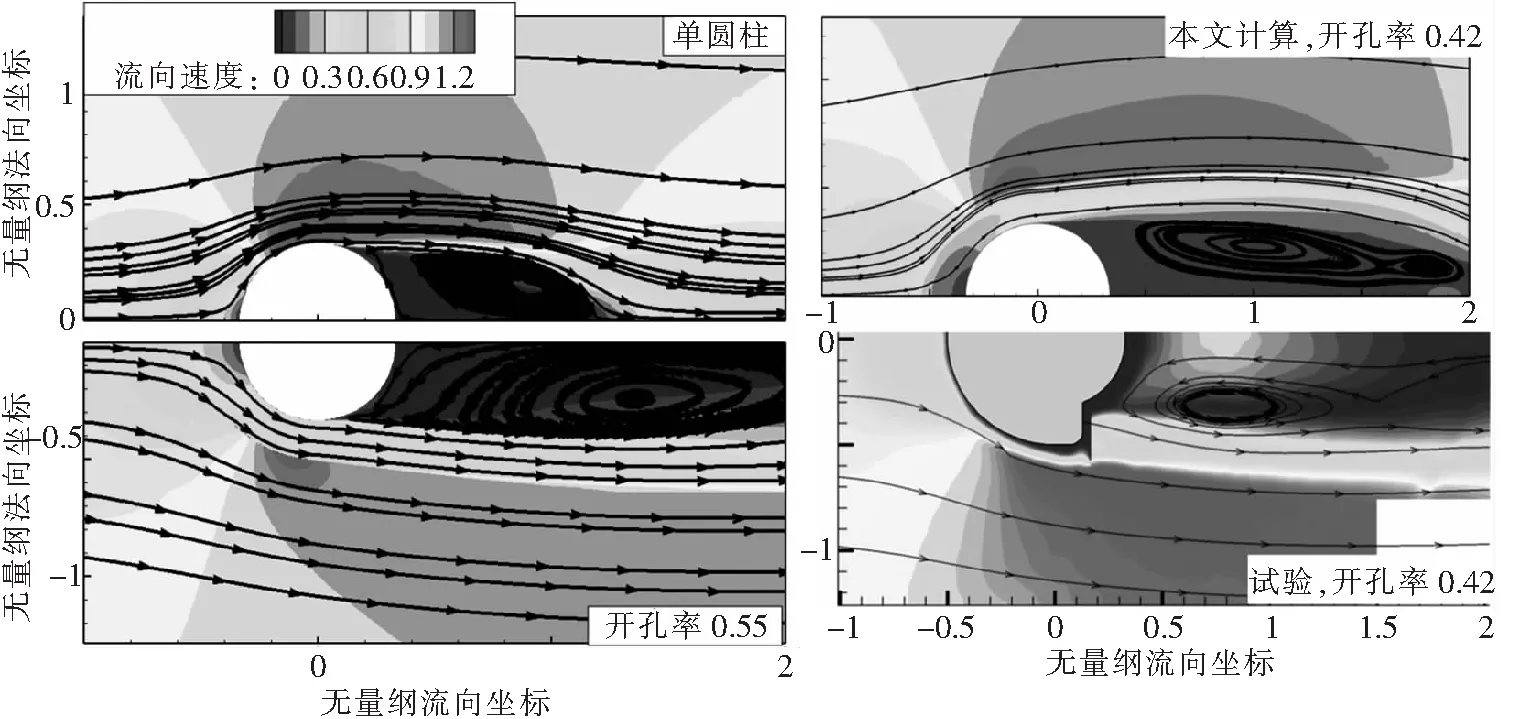
圖7 不同算例平均流場對比(以阻尼網的直徑Df為基準進行無量綱化)

圖8給出了無量綱流向速度和湍動能沿流向線(=0.0)分布。單圓柱和阻尼網開孔率為0.42時，均表現(xiàn)為典型的圓柱分離特征。如此低開孔率的阻尼網使得整流罩趨向于一個不可穿透的半圓柱，相當于增大了單圓柱的直徑，表現(xiàn)為更大的分離區(qū)和更高的湍動能峰值。阻尼網開孔率為0.55時，更多的流體流向單圓柱，使得整流罩尾部形成類混合層結構。該混合層極大地增大了分離區(qū)，也降低了分離區(qū)內速度的不均勻程度和湍動能。

圖8 無量綱流向速度和湍動能沿流向線的分布(y/D=0.0)

圖9給出了監(jiān)測點(=265,=-06)處法向速度的功率譜密度。阻尼網開孔率為042時，仍然存在明顯的渦脫行為，其無量綱的渦脫頻率為019；若以阻尼網直徑為無量綱基準，則無量綱頻率為0285，符合此雷諾數(shù)下圓柱繞流的渦脫特點。阻尼網開孔率055時功率譜密度表現(xiàn)為寬頻行為，無渦脫現(xiàn)象。

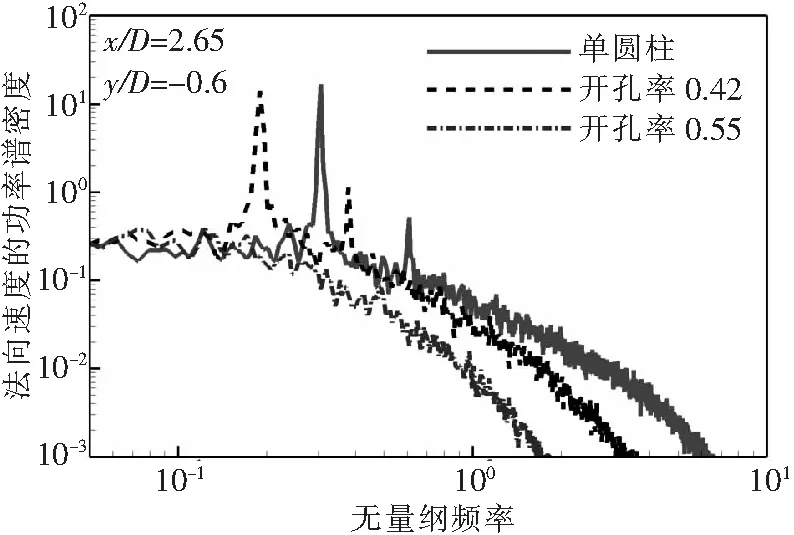
圖9 監(jiān)測點法向速度的功率譜密度

因此，阻尼網能夠改變單圓柱的分離區(qū)和渦脫特性，從而影響近場的湍流脈動；合適的開孔率能夠消除單圓柱的渦脫行為，從而極大地降低湍流脈動。

圖10給出了90°輻射角度上遠場噪聲的功率譜密度，遠場麥克風距離圓柱圓心距離=185。作為對比，來自文獻的試驗結果顯示在左圖。遺憾的是，文獻中沒有給出具體的數(shù)值。但是，從圖中可以看出，在試驗中開孔率為0.55時能夠抑制主導頻率處的噪聲；而本文的計算重現(xiàn)了這個控制效果。同時，開孔率0.42時，噪聲中存在0.19的無量綱主導頻率，該頻率處的幅值為71.5 dB，比單圓柱峰值低2.5 dB，但其在中高頻率的能量均高于單圓柱噪聲。

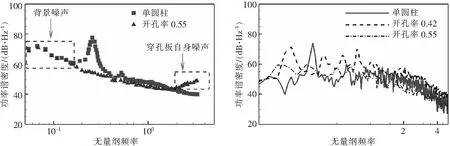
圖10 90°輻射角度處噪聲功率譜密度的對比

圖11給出了三個算例中的總聲壓級的對比。開孔率為0.55時，阻尼網減小了單圓柱的輻射噪聲，在90°方向上的降低量為3.5 dB；而開孔率為0.42時則增大了單圓柱的輻射噪聲，相同角度上的增大量為4.1 dB。阻尼網降低單圓柱噪聲時需要有合適的開孔率，過小的開孔率反而會使得噪聲增加。

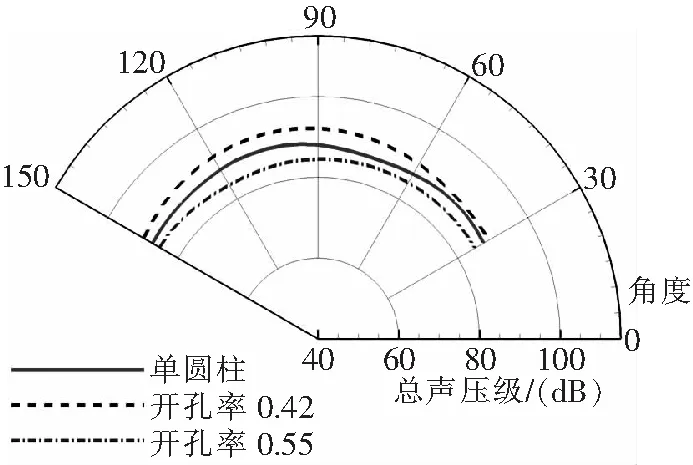
圖11 遠場總聲壓級的對比

4 總結

本文探索了阻尼網控制單圓柱振動和噪聲輻射的機理，為阻尼網在直升機流動控制中的應用奠定理論基礎。計算中流場的模擬采用IDDES方法，遠場噪聲采用FW-H方程，阻尼網區(qū)域采用阻尼網模型。

使用防風柵算例對本文計算方法驗證之后，采用開孔率0.42和0.55的兩個阻尼網研究其對振動和噪聲的控制機理和控制規(guī)律。阻尼網通過控制單圓柱的分離區(qū)和渦脫特性來影響近場振動和遠場噪聲。開孔率為0.42時，相當于增大了單圓柱的直徑，表現(xiàn)為更大的振動和噪聲。開孔率為0.55時，阻尼網降低了單圓柱分離區(qū)的不均勻性，消除了渦脫，極大地降低了振動，無量綱湍流脈動最大值從0.19降到0.09。在遠場噪聲方面，該阻尼網能在90°方向降低總聲壓級3.5 dB。