輪式機器人分數階滑模內模速度控制器設計
王 鑫 劉怡明 王明明* 孫曉云
1(石家莊鐵道大學電氣與電子工程學院 河北 石家莊 050043)2(蘇州大學機電工程學院 江蘇 蘇州 215137)
0 引 言
輪式機器人具有速度快、效率高的優點,廣泛應用于礦山檢測、市政檢測等領域[1-2]。針對輪式機器人無刷直流電機(Brushless Direct Current Motor,BLDCM)驅動系統,傳統PID控制策略,速度響應慢、抗干擾能力差、過度依賴精確的數學模型,文獻[3-4]將模糊控制與PID結合,雖然不需要精確的數學模型,但隸屬度函數的選取需要大量的經驗,難達到最好的效果。文獻[5-6]將滑模控制應用于BLDCM調速系統,使系統參數變化時不受影響,在內外擾動下系統具有良好的魯棒性,但滑模控制易出現系統抖振。文獻[7]采用指數趨近律滑模算法對BLDCM進行調速控制,但在原點處存在帶狀高頻抖動。文獻[8]將神經網絡與滑模控制結合,抑制了系統抖振,但未考慮調節時間。文獻[9]將分數階滑模控制應用于消除永磁同步電機系統抖振,同時使系統具有較少的響應時間。文獻[10]將內模控制應用于消除內環干擾,使整個系統具有干擾抑制特性。
本文在深入研究輪式機器人運動方式與BLDCM調速的基礎上,結合分數階滑模控制與內模控制提出一種輪式機器人分數階滑模內模調速新方法。為了驗證算法的有效性,通過搭建MATLAB/Simulink與Carsim 聯合仿真平臺,在不同路面擾動的情況下進行啟動加速與速度突變的仿真實驗。實驗結果表明,分數階滑模內模速度控制器可以有效地降低速度響應時間,消除干擾,提高系統的魯棒性。
1 輪式機器人模型建立
1.1 Carsim簡介
Carsim是用于車輛動力學的專用仿真軟件,可以模擬道路和空氣動力輸入的響應,并且主要用于預測和模擬總體車輛操縱穩定性。本文借助Carsim的路面輸入響應,進行輪式機器人在不同路面下的仿真實驗,用于輪式機器人速度控制器的開發。
1.2 BLDCM數學模型
針對BLDCM為兩相導通星形三相六狀態的情形,在理想狀態下,三相繞組的電壓平衡方程式為:
(1)
式中:Ua、Ub、Uc為三相繞組的相電壓;ea、eb、ec為三相繞組的反電動勢;ia、ib、ic為三相繞組的相電流;M為各相繞組之間的互感;r為各相繞組的電阻;L為各相繞組的自感。BLDCM定子繞組產生的電磁轉矩可表示為:
(2)
式中:Te為電磁轉矩;ω為電機機械角速度。運動方程為:
(3)
式中:TL為負載轉矩;J為電機轉動慣量;B為阻尼系數。
1.3 輪式機器人差速運動模型建立
為了輪式機器人更加靈活、轉彎半徑更小、適應更多的路況,建立前后四輪差速控制模型,將輪式機器人抽象成前、后兩個轉向模型進行分析,前后輪差速轉向模型的轉矩分配狀態直接由轉向模型進行確立。模型中內外輪的轉矩比為:
(4)
式中:W為輪距;H為輪式機器人質心到地面的高度;w為電機機械角速度;V為輪式機器人速度;g為重心加速度;θ為轉向角度。在轉向過程中,內外側輪的轉矩差為ΔTp:
(5)
輪式機器人內外側輪在轉向過程中所需的實際轉矩分別為:
Tin=Te-ΔTp
(6)
Tout=Te+ΔTp
(7)
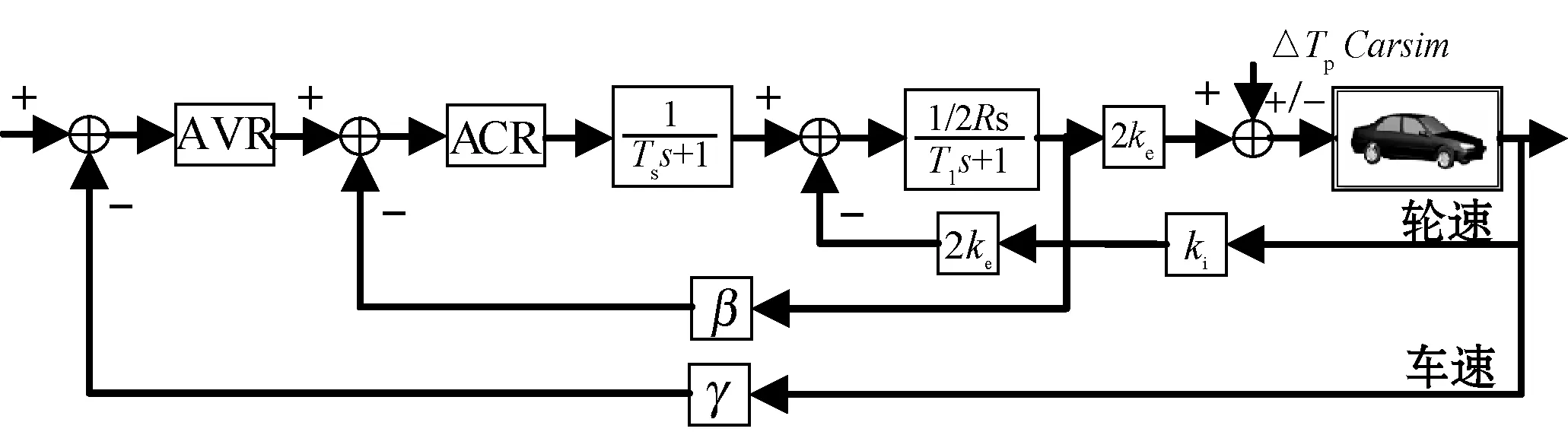
根據輪式機器人運動方式,利用MATLAB/Simulink與Carsim建立四輪差速運動模型,通過Simulink和Carsim的接口設置來完成輪式檢測機器人的驅動系統與整車模型之間的信號傳遞, 實現將電機轉矩直接加載到車輪上。每一個車輪由一個BLDCM進行控制。Carsim系統輸入輸出如表1所示。
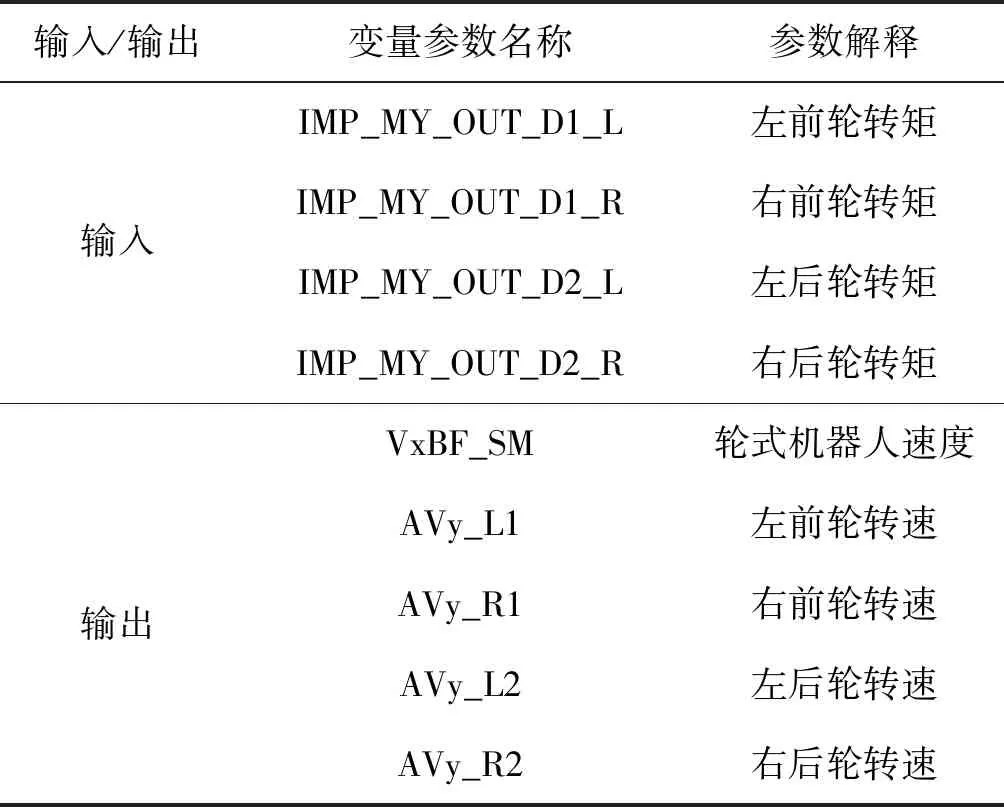
表1 Carsim系統輸入輸出
Simulink和Carsim控制結構如圖1所示。
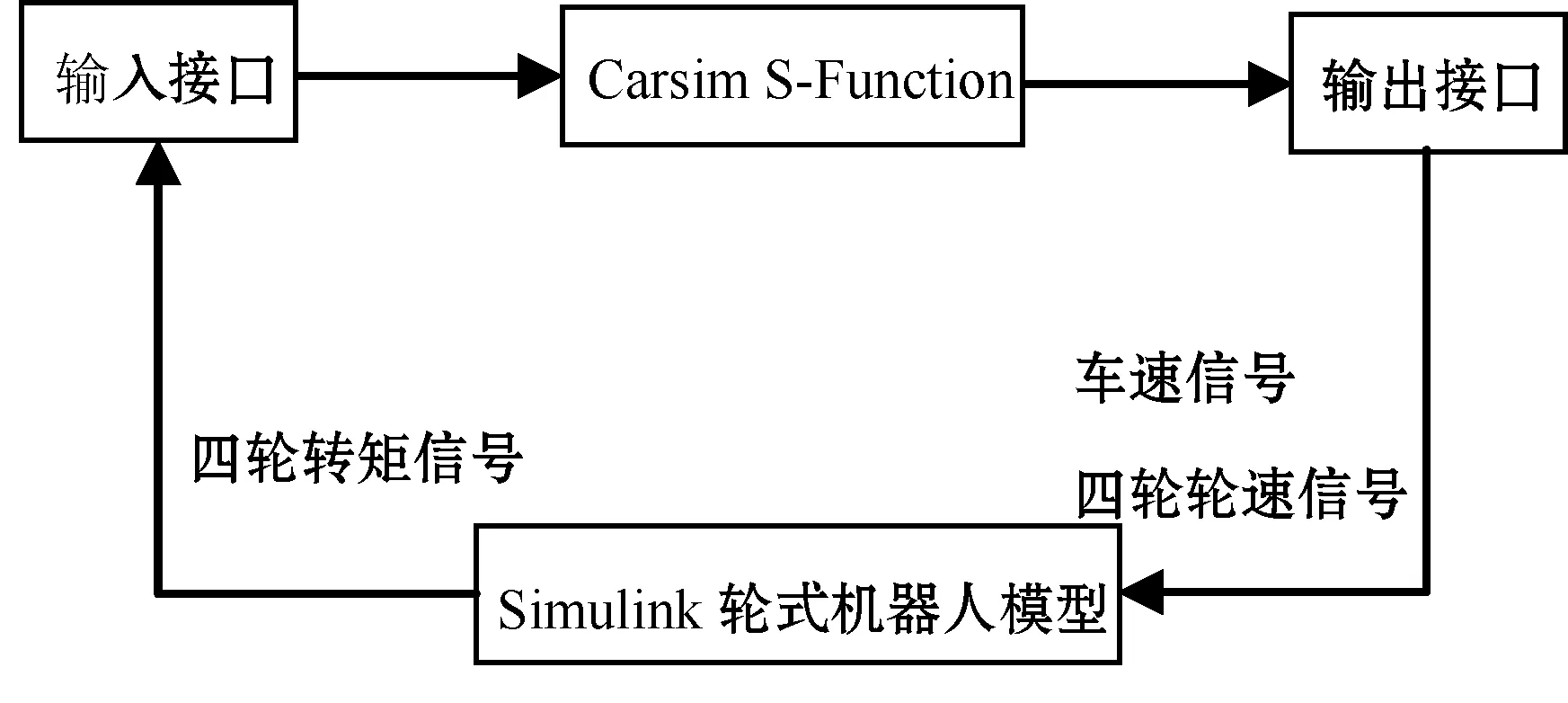
圖1 控制結構
2 輪式機器人調速系統設計
2.1 分數階滑模控制簡介
分數階滑模控制是由分數階算子與滑模控制結合而成的。一般將分數階微積分的基本操作算子定義為aDta,具體形式為:
(8)
式中:a為階次,Re(a)為其實部;α是操作算子的下限,t為上限;τ為積分的導數。
隨著對分數階的認知與分析,常用的為Grünwald-Letnikov(GL型)、Caputo(C型)和Riemann-Liouville(RL型)。
其中RL型分數階微積分定義為:
(9)
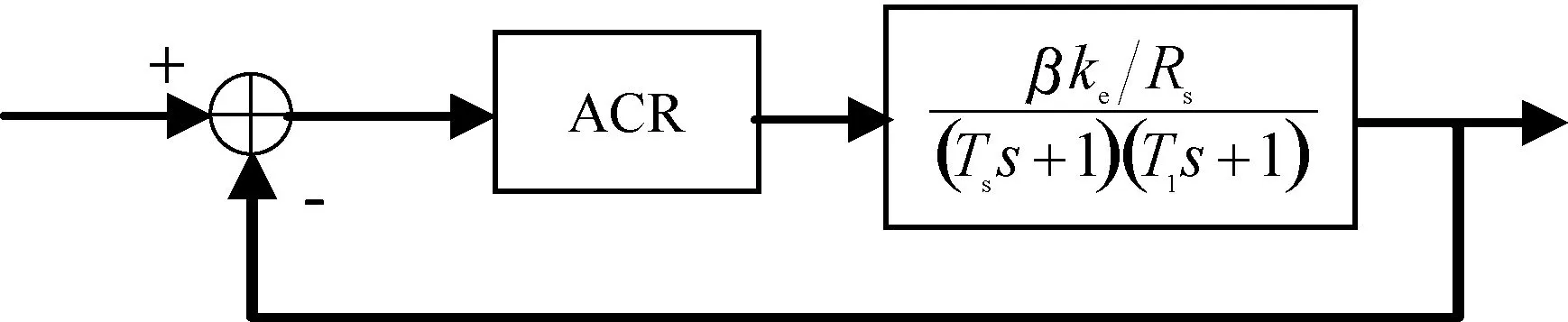
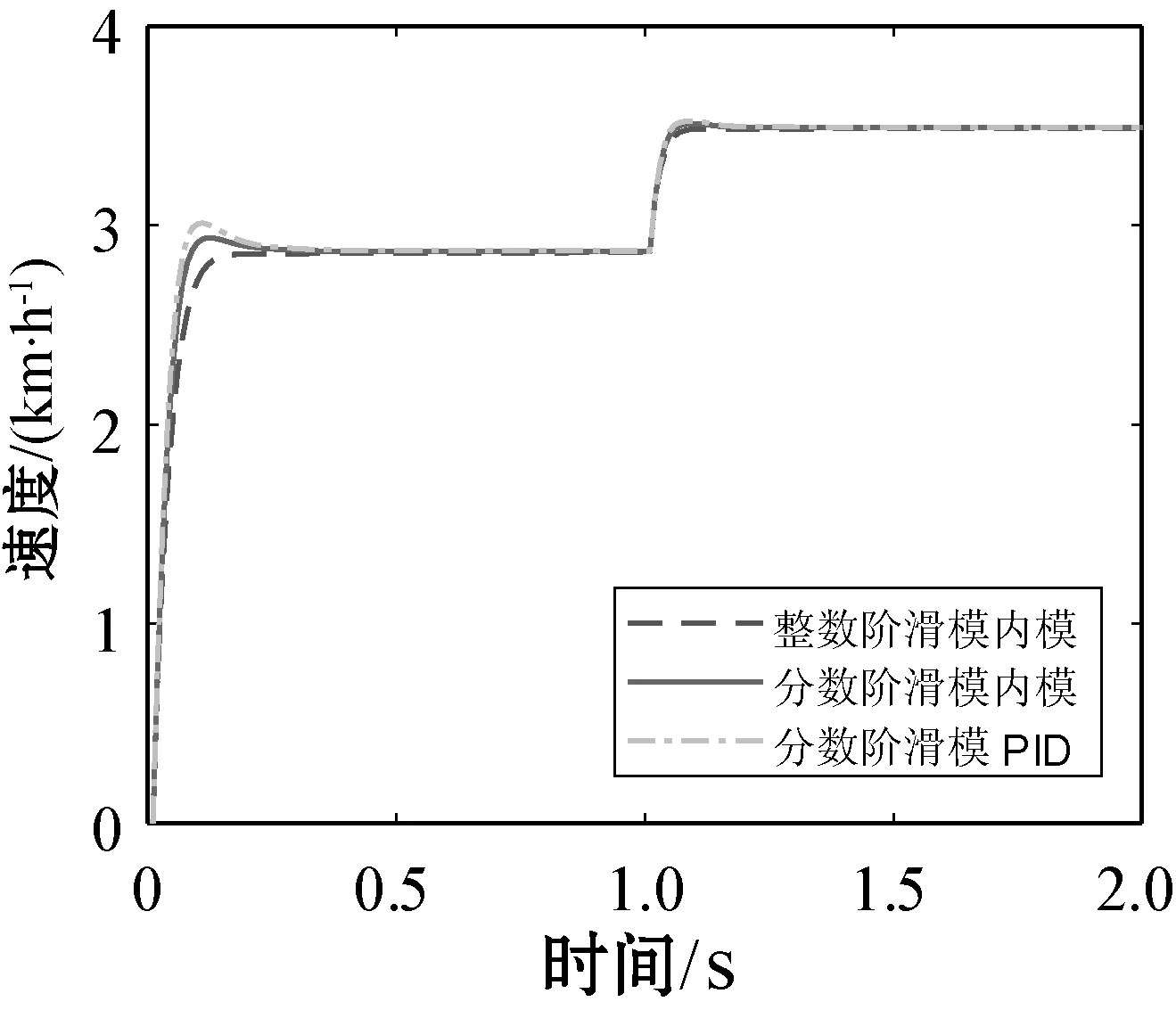
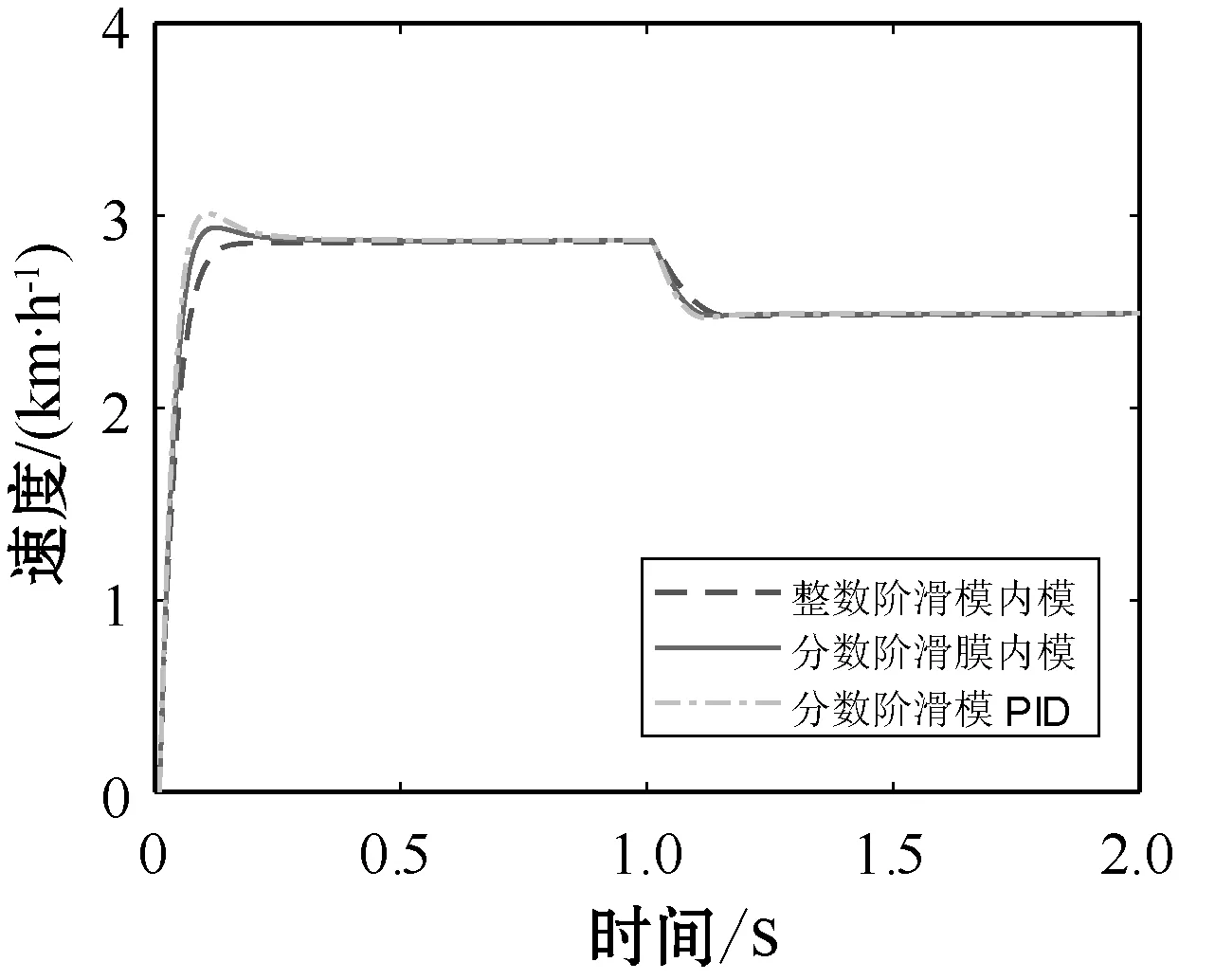
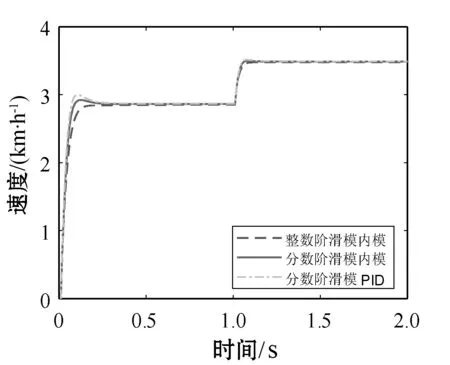
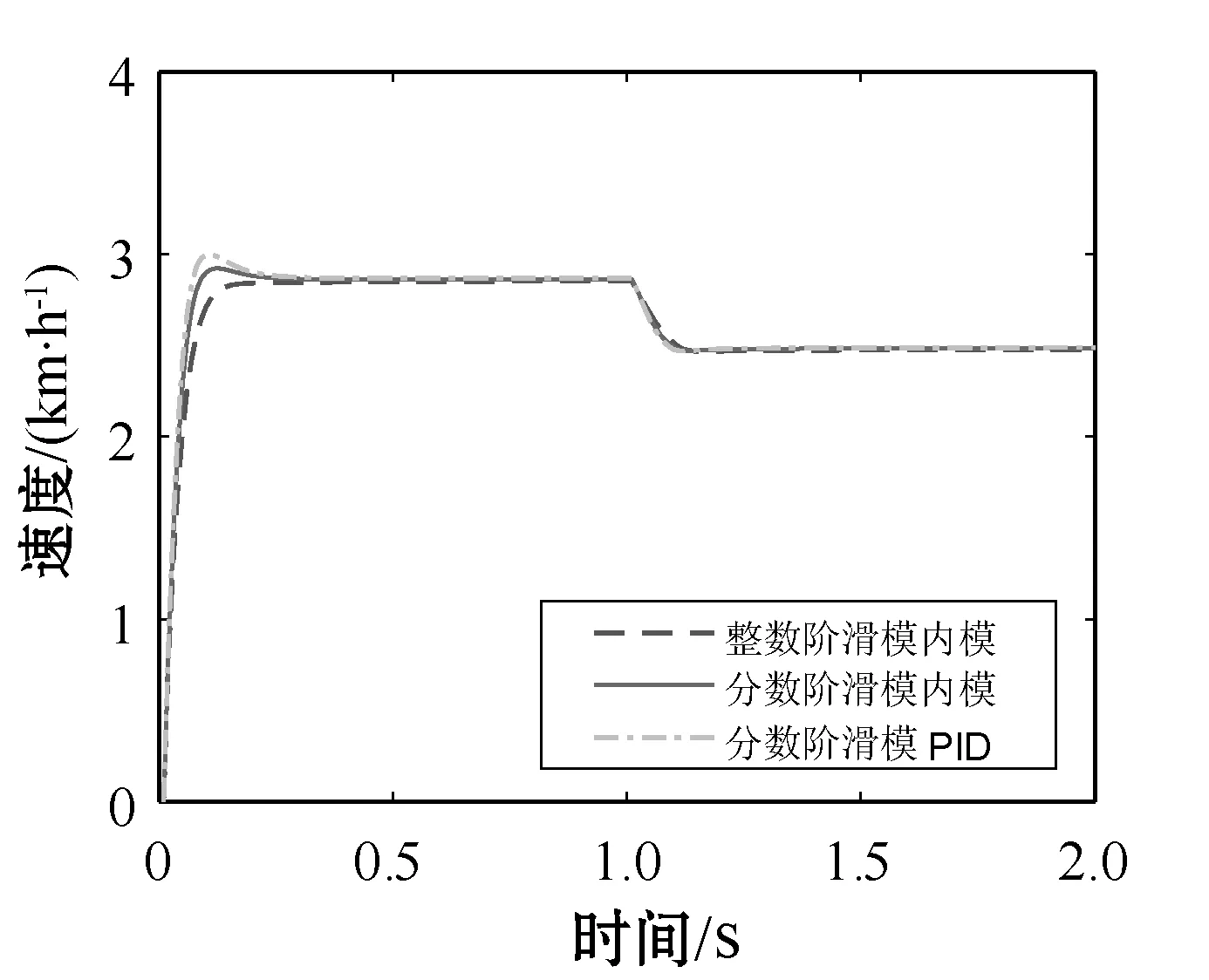
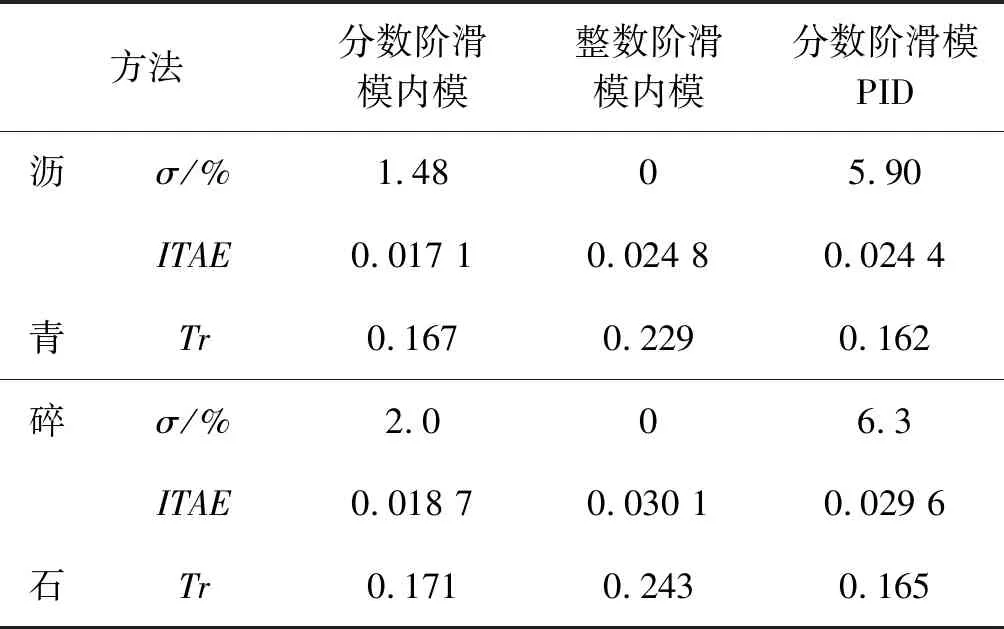
式中:m∈N;a滿足m-1 RL函數的分數階積分的Laplace變換為: L[αDt-af(t)]=s-aL[f(t)]=s-aF(s) (10) 利用BLDCM數學模型,忽略粘滯摩擦系數的影響,改進式(3)為: (11) 則BLDCM的狀態方程為: (12) 式中: (13) (14) 電流i為輸出,轉速偏差為輸入。 取分數階積分滑模面為: (15) 式中:c為滑模面增益,且c>0。指數趨近律為: (16) 式中:ε>0;k>0。 則分數階滑模控制的控制結果為: (17) 分數階滑模控制的結果,使得輸出的電流變為分數階積分,降低了電流環輸入的波動,提高了系統魯棒性。 采用李雅普諾夫穩定性來分析分數階滑模控制的有效性,設李雅普諾夫函數為: (18) 對其求導得: s×[-εsgn(s)-ks]= -εs·sgn(s)-ks2 (19) 加入干擾項后,有新的狀態方程: (20) 為了滿足李雅普諾夫函數,有: (21) 結合內模控制器原理可知,內模控制系統輸出為: (22) 式中:R(s)為系統輸入;Y(s)為系統輸出;CIMC(s)為內模控制器;G(s)為實際被控對象;GM(s)為被對象數學模型;D(s)為擾動。 根據BLDCM結構,電流環結構如圖2所示。 圖2 電流環結構 假定被控對象與模型匹配,則: (23) 根據內模控制器的設計原則,將模型GM(s)分解成: GM(s)=GM+(s)GM-(s) (24) 式中:GM-(s)具有最小相位特征,而GM+(s)則為模型非最小相位部分,包含時滯環節和右半平面零點。 為保證內模控制器的可實現性,提高系統的穩定性和魯棒性,引入低通濾波器f(s),將電流內環看成一階慣性系統,則電流內模控制器CIMC(s)為: (25) (26) 則電流環內模控制器傳遞函數為: (27) 存在λi使得: Y(s)=R(s) (28) 從式(27)與式(28)容易看出,電流環內模控制器只需調節一個參數λi,使得控制參數調節更加簡便,并且可以消除負載變化帶來的干擾D(s),從而提高系統的魯棒性。 為了驗證分數階滑模內模調速方法的優越性,利用MATLAB/Simulink與Carsim軟件進行仿真實驗,并與整數階滑模內模控制、分數階滑模PID控制進行對比分析。 以輪式機器人速度作為外環,根據實際速度與設定的速度偏差進行控制,使輪式機器人速度快速地跟隨給定速度變化,電流環作為內環,速度環的控制輸出作為電流控制的輸入,緊緊跟隨速度環的變化進行控制,最后結合Carsim反饋的輪式機器人輪速信息,完成整個系統的控制。速度環和電流環分別由控制器AVR和ACR控制,速度控制器AVR使用分數階滑模控制器;電流控制器ACR為內模控制器。輪式機器人調速系統(單個輪子)動態結構如圖3所示。 圖3 輪式機器人調速系統(單個輪子)結構 設定輪式機器人車長:820 mm;車寬:695 mm;車高:356 mm;車重:65 kg;車輪半徑:150 mm;輪距:602 mm;軸距:504 mm;電機額定功率5 kW;電阻(Rs):0.125 Ω;電感(T1):3.75 mH;反電動勢(ke):0.25 V·(r·min)-1;電流反饋系數(ki):36;PWM延遲系數(Ts):0.4。 在Carsim中,根據不同的地面滾動摩擦系數與滑動摩擦系數,選取瀝青與碎石兩種不同的路面擾動進行仿真實驗。設置啟動速度為2.88 km/h,突然加速實驗在1 s時速度由2.88 km/h變為3.50 km/h;突然減速實驗在1 s時速度由2.88 km/h變為2.50 km/h。 根據所建模型,首先在瀝青地面的情況下進行仿真實驗。瀝青地面突然加速過程如圖4所示。 圖4 瀝青地面突然加速過程 瀝青地面突然減速過程如圖5所示。 圖5 瀝青地面突然減速過程 根據參數設置對碎石路面進行仿真實驗,碎石地面突然加速過程如圖6所示。 圖6 碎石路面啟程突然加速過程 碎石地面突然減速過程如圖7所示。 圖7 碎石地面突然加速過程 由圖4-圖7可知,分數階滑模內模在輪式機器人速度變化過程中,速度快速跟隨到設定值且基本上無超調。為了進一步證明本文算法的有效性,選取超調量σ、上升時間Tr與時間乘絕對誤差積分準則ITAE進行評估,對圖4、圖6前1 s數據進行處理,數據處理結果如表2所示。 表2 數據處理結果 由表2數據分析可知,在不同的地面干擾情況下,分數階滑模內模控制較分數階滑模PID控制在保持快速性的同時降低了系統超調;分數階滑模內模控制速度響應優于整數階滑模內模控制,且在保持快速性的同時只存在少量的超調,證明控制系統具有良好的動態響應;從ITAE指標也可以看出,分數階滑模內模控制瞬態響應的振蕩性小。 綜上所述,分數階滑模內模速度控制器對于外部干擾具有較強的抗干擾能力、響應速度快、響應速度曲線波動小,能夠快速達到設定速度,并以設定速度平穩運行。 在不同路面的擾動下,為了提高輪式機器人的響應速度,降低外部擾動對調速系統的影響,改善系統抖振。本文在輪式機器人無刷直流電機調速系統的基礎上,結合分數階滑模控制與內模控制策略,提出一種調速控制新方法。通過搭建MATLAB/Simulink與Carsim聯合仿真平臺,與分數階滑模PID控制和整數階滑模內模控制進行對比實驗,實驗結果表明,分數階滑模內模控制器能有效降低速度響應時間,減少擾動對速度控制的影響,消除系統抖振,提高系統的魯棒性,可應用于以速度調控為主導的控制系統。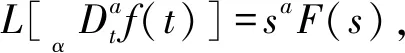
2.2 速度環分數階滑模控制
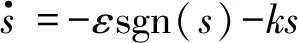
2.3 分數階滑模穩定性分析
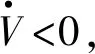
2.4 電流環內模控制
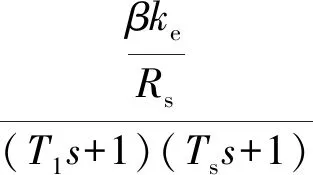
3 系統仿真與分析
3.1 仿真平臺
3.2 仿真效果分析
4 結 語

