探求附條件多元連續函數的極值點
揭 勛
(廣東文理職業學院,廣東 廉江 524400)
“多元連續函數的條件極值”是高等數學的教學重點和教學難點,該問題的解決在實際應用上具有重大意義.現行高職院校數學教材在介紹的拉格朗日乘數法時[1-2],僅通過建立拉格朗日函數,求出其駐點,認為其駐點就是附條件多元連續函數的可能極值點,而對于拉格朗日函數的建立理由、其駐點為何是可能極值點、如何判斷這些可能極值點是否為必然的極值點、除了這些駐點外是否還存在其他可能極值點(比如拉格朗日函數的不可微點)等問題,并沒有作系統性的介紹,這容易影響學生對該類問題的全面掌握.
本文在充分參考拉格朗日乘數法求多元連續函數條件極值[3-4]的基礎上,探索利用有效的方法,把所有可能的極值點探求出來,并從中判斷出必然的極值點,從而全面地解決附條件多元連續函數的極值求解問題.
1 探求附條件多元連續函數極值點的思路導入
設f(x1,x2,…,xn)是在所附條件為φk(x1,x2,…,xn)=0 (k=1,2,…,m;其中m 一般地,當n=2時,在空間直角坐標系下,二元連續函數u=f(x1,x2)在所附條件φ(x1,x2)=0下的圖像是某一連續的曲線;當n≥3時,在n+1維空間中,附條件n元連續函數u=f(x1,x2,…,xn)的圖像已經沒有直觀的幾何意義了,但根據多元函數的定義以及多元連續函數極值點的定義,對應于函數值的那一維度(或者坐標軸)向上翹突起來的點或者向下陷落的點,便分別是附條件多元連續函數的極大值點和極小值點. 附條件n元連續函數的極值點必是該附條件n元連續函數的駐點或者不可微點,附條件n元連續函數的駐點或者不可微點不一定是該附條件n元連續函數的極值點[5]. 利用前述n+1維向量空間中向量之間的關系,從幾何的角度入手,探求并得出拉格朗日乘數法中由拉格朗日函數的各個偏導數組成的方程組[7],從而求出附條件多元連續函數的其中一類可能極值點(駐點).這個方法比拉格朗日乘數法的證明過程較為形象易懂,教學上易為學生所理解. 利用n元連續函數f(x1,x2,…,xn)及φk(x1,x2,…,xn)的偏導數,可以求出n元連續函數u=f(x1,x2,…,xn)的不可微點中,滿足所附條件φk(x1,x2,…,xn)=0(k=1,2,…,m;其中m 求出附條件n元連續函數u=f(x1,x2,…,xn)的每個可能極值點后(包括駐點和尖點),再利用附條件n元連續函數極值點處的函數圖像特征,可以判斷每個可能極值點是極大值點還是極小值點,并求出每個極值,方法如下: 例1求二元函數z=f(x,,y)=6x2-xy+19y2在所附條件為φ(x,y)=x+y-56=0下的極值. 解先求該二元連續函數在所附條件為φ(x,y)=x+y-56=0下的駐點. 其中,兩個累次極限分別為: =|12x-y+λ| =|-x+38y+λ| 故,點(42,14)是該二元連續函數在所附條件下的一個駐點,也是一個可能極值點(注:這個駐點也可以采用拉格朗日乘數法求得,求出的結果是相同的). 下面分析(42,14)這個駐點是不是該二元連續函數在所附條件下的必然的極值點: 故,駐點(42,14)是該二元連續函數在所附條件下的一個極小值點,其極小值為13 720. 在點(0,0,…,0,9)處,由于 在高等數學微積分學知識板塊中,多元連續函數的極值問題與經濟應用、社會應用中的最優化策劃問題關聯密切[9],是實際應用最廣泛的課題之一.本文利用n維向量空間中,向量之間的相互關系,通過構建可能極值點處的相關數學模型,經過有效的分析論證,運用重極限和累次極限的計算等途徑,全面系統地探索附條件多元連續函數的全部可能極值點,并對求解出來的每個可能極值點是否必然的極值點,提出了行之有效的判斷方法,為全面解決附條件多元連續函數的極值問題提出一種可行的思路.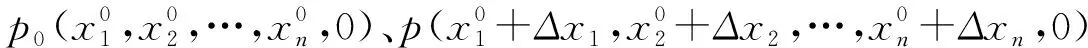
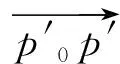
2 關于附條件多元連續函數的駐點
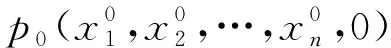
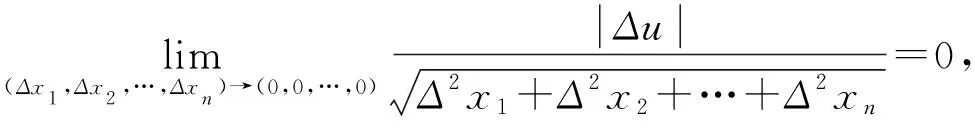

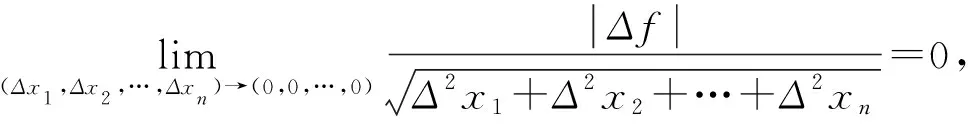
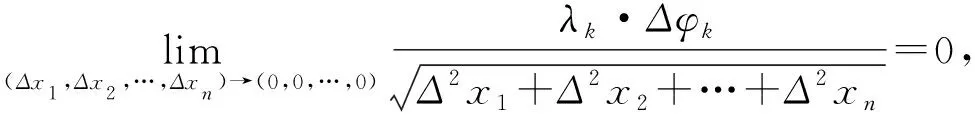
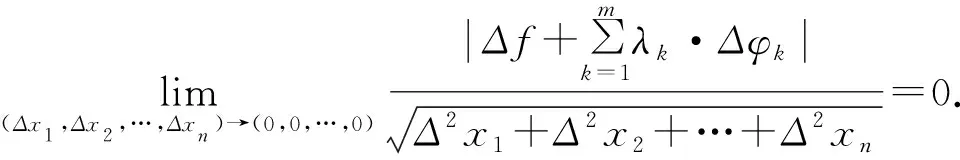
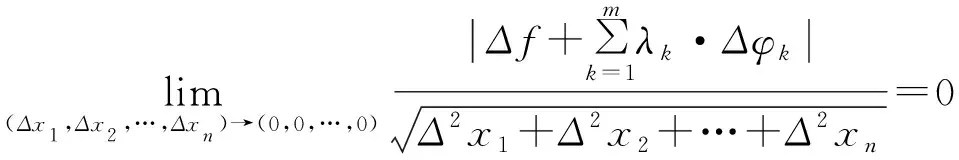
3 關于附條件多元連續函數的尖點
4 判斷附條件多元連續函數的駐點和尖點是否極值點
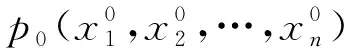
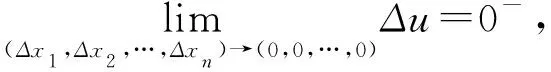
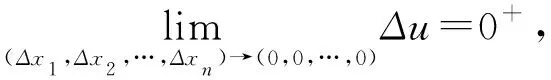
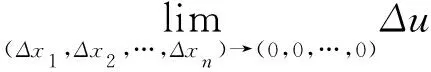
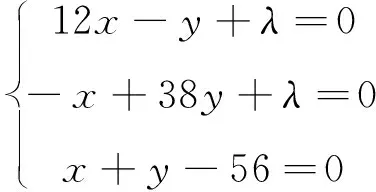
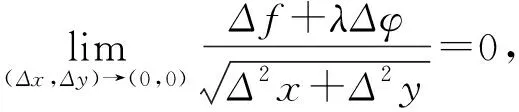
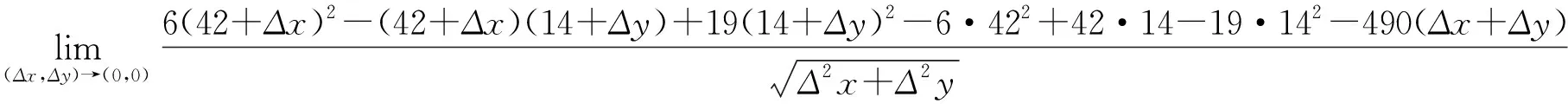
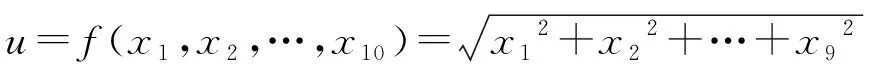
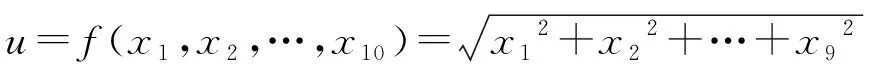
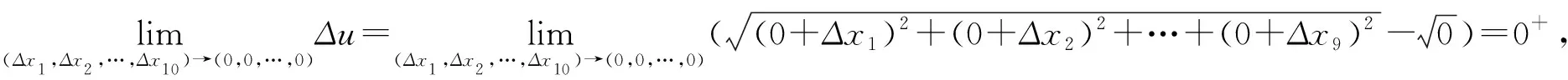
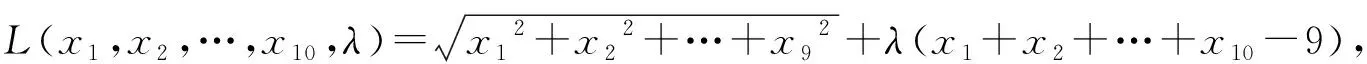
5 結語

