尺規作圖的教學價值新厘定及教學路徑新視角




摘 要 “尺規作圖”是新修訂的小學數學課程標準“圖形與幾何”領域中的新增內容,如何認識尺規作圖在教學中的重要地位及其教育價值,提升學生數學核心素養?須重新厘定尺規作圖的教學價值并以新的視角規劃教學路徑。首先明晰尺規作圖的教學價值:借尺規作圖鍛煉學生動手操作能力,借尺規作圖發展學生幾何直觀水平,借尺規作圖促進學生邏輯思維的形成,借尺規作圖積淀學生數學核心素養;其次從歷史視角、思維視角、發生學視角三個方面闡述“尺規作圖”的教學路徑。
關? 鍵? 詞 尺規作圖 幾何學科育人價值 培育數學核心素養
引用格式 芮金芳.尺規作圖的教學價值新厘定及教學路徑新視角[J].教學與管理,2022(08):51-54.
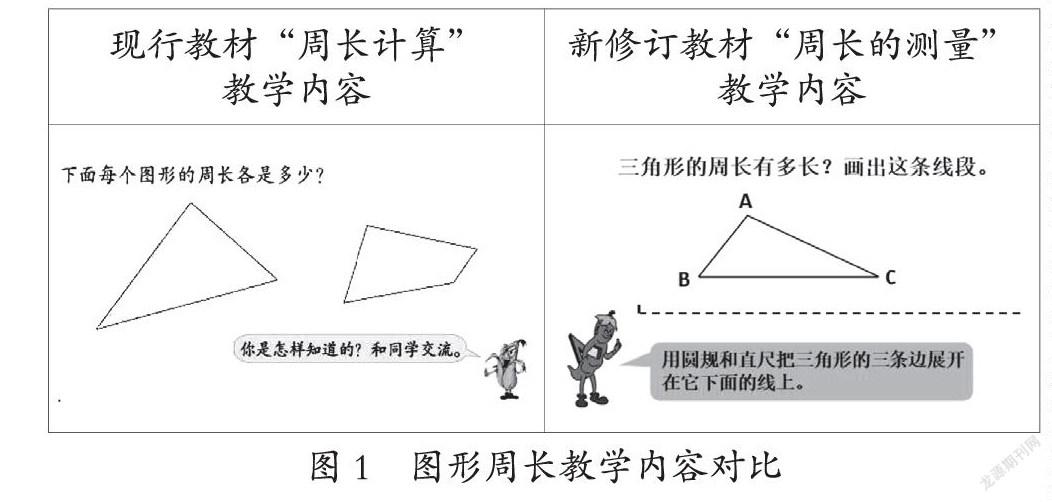
最近,筆者參加江蘇省小學數學教材培訓暨“測量”專題教學研討活動,觀摩兩位教師同課異構執教“周長的測量”一課,其中有一個環節引發筆者的思考。新教材在學生初步認識周長概念以后,要求他們用“尺規作圖”的方法得到圖形周長的測量結果。這與現行教材中的“周長計算”的目標要求、呈現方式明顯不同(如圖1)。
一、尺規作圖在課標修訂中的變化
關于“圖形與幾何”領域中的作圖,《義務教育數學課程標準(2011年版)》和新修訂課程標準分別提出了相應的內容要求[1](見表1)。
關于“圖形與幾何”領域的作圖,2011年版課程標準在小學階段只是要求掌握畫圖的技能和方法,而沒有尺規作圖的具體要求,從而使一線教師對此內容的教學無章可循。畫圖和作圖雖然只有一字之差,但要求卻不盡相同。新修訂課標提出“幾何更注重直觀,增加尺規作圖”。可見,小學階段特別是中、高年級明晰教學中對尺規作圖的要求,理解尺規作圖獨特的教學價值,對培養學生的空間觀念、幾何直觀、推理能力具有極其重要的作用。
二、尺規作圖教學價值新厘定
尺規作圖最早起源于古希臘的數學課題,是指用無刻度的直尺和圓規,在有限次數的前提下,解決不同的平面幾何作圖問題[2]。尺規作圖的問題是歐式平面幾何中的核心內容,借助作圖這一直觀手段,不僅可以豐富學生的幾何知識,而且對培育學生的空間觀念具有重要的價值。
1.借尺規作圖鍛煉學生動手操作能力
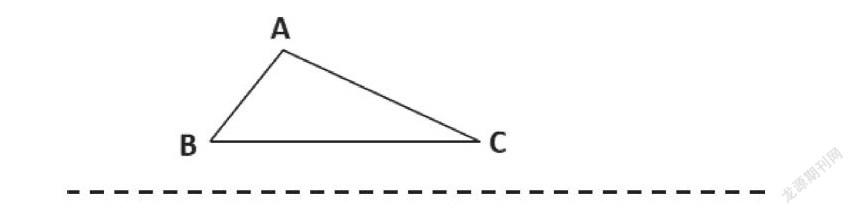
新修訂課標對“尺規作圖”的整體目標要求是增加動手操作環節,增強學生對數學的感覺。根據小學生的年齡和心理特點,好動是其天性,要發展他們的空間觀念,主要依靠用眼觀察和動手操作,而尺規作圖是學生在多種數學工具支持的場景下,開展動腦思考、動手做數學的挑戰性創造活動。在“周長的測量”一課中,學生初步感知圖形一周邊線的長就是它的周長這一概念后,出示任意一個三角形,布置動手操作任務。
提出問題:你準備怎樣測量三角形的周長?
作圖工具:圓規、直尺。
作圖要求:
(1)畫一畫:用圓規和直尺把三角形的三條邊展開在下面的線上。
(2)量一量:測量出三角形的周長,記錄下來。
(3)說一說:與同伴交流你是怎樣得到三角形周長的。
在核心問題的引領下,學生利用作圖工具——圓規和直尺動手操作,學生在動態的作圖轉化過程中深刻體會到:用圓規能準確刻畫出與三角形三邊相等的等長線段,圓規作出的線段AB、線段BC、線段CA′的長度與三角形三條邊對應等長,更深刻地感悟圖形周長含義的本質內涵——環繞有限面積的區域邊緣的長度積分。在這一手腦并用的做數學過程中豐富學生對“周長”概念的理解,使學生的認識逐漸從膚淺走向深刻、從單一走向豐滿、從粗略過渡到精準。
2.借尺規作圖發展學生幾何直觀水平
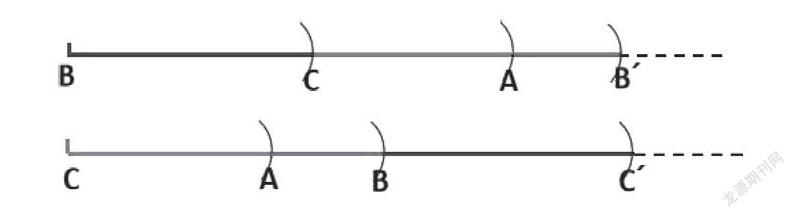
數學家阿蒂亞說過:在幾何中,視覺思維占主導地位。幾何直觀是一種特殊的形直觀,而尺規作圖在學生實際操作的過程中具有不可替代的直觀性。教師可以利用尺規作出的精準圖形,從形象、直觀的思維視角引導學生觀察、思考、分析,憑借簡潔、直觀的載體巧妙解決數學問題,促進學生思維由具體直觀逐步向更高級、更抽象的空間形式轉化,有助于學生直觀想象能力的培養,使其形成良好的思維品質。在“周長的測量”教學中,學生利用尺規作圖,將三角形周長轉化成線段AA′的長度后,利用直觀構圖引發思考“線段AA′為什么是三角形的周長?”“除了可以從點A展開三角形的三條邊,還可以怎樣展開?”
學生在作圖過程中,能直觀、具象地感受到線段AB、線段BC、線段CA′與線段AA′之間的關聯,即AB+BC+CA′=AA′,基于這一等量關系的確定,如果從點B、點C展開三角形的三條邊,同樣可以發現具有等量關系的式子,即BC+CA+AB′=BB′、CA+AB+BC′=CC′。在比較中學生發現雖然作圖時展開的位置、順序不一樣,但它們的總和始終是不變的確定量,這就進一步豐富了學生對周長概念內涵的深刻理解,周長等于圖形所有邊的和,與邊的前后順序無關。
同時,學生借助作圖中線段長度的直觀模型,可以簡明、清楚地表示測量圖形周長的兩種方法:既可以分段測量再求和,也可以展開后測量得到。在尺規作圖中具體、豐富的形使得問題的解決更容易,使抽象的關系與外在可感的圖式建立有力的聯結,成為進一步深入探索問題的工具,甚至能形成學生較強的直觀洞察力。
3.借尺規作圖促進學生邏輯思維的形成
尺規作圖不應簡單地界定為一種動手操作。尺規作圖前學生要先觀察、分析、思考、預測、判斷,再動手作圖。尺規作圖不僅要讓學生在作圖之后知曉為什么這樣作的道理,更要讓學生在作圖之前知道這樣操作的原因。小學階段的尺規作圖讓學生思維從操作實驗的具象直觀,逐步向推理論證的嚴謹抽象過渡。
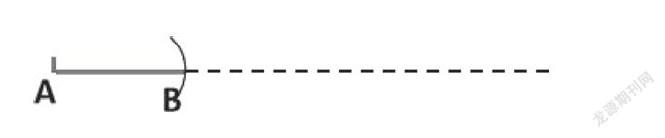
在“周長的測量”一課中,學生借尺規作圖將三角形中一條邊轉換成線段AB,引導學生根據線段AB的長度和位置,來推斷思考線段BC中點C的位置大概在什么地方?學生借助已有的作圖經驗,綜合多個信息執果索因,進行逆向思考,從而確定點C、點A′的位置。
此時教師依據作圖探究過程,讓學生圍繞兩個關鍵問題整體思考:你是怎樣想到要在這里作這個點的?為什么這樣作圖是正確的?讓學生不斷進行學習的自我監控,在回望作圖操作的過程中加深對周長含義,以及三條線段長度和與線段AA′之間等量關系的理解,同時為周長計算方法的呈現提供了“推理論證”的思維雛形。所以,理解尺規作圖的步驟,對培養學生嚴密的邏輯推理能力,深刻的探索性思維,乃至初中階段的嚴格證明都有積極的影響。
4.借尺規作圖積淀學生數學核心素養
學生每次作圖在紙面上留下的作圖痕跡與簡單推理,都是學生嘗試、分析、思考、論證的邏輯思維過程的具體體現。新修訂課標中引入尺規作圖不單單是要求學生會作圖,更是學生具身動手操作學習的直接體現,也間接蘊伏了學生邏輯推理能力、幾何證明能力的培養,使學生感受邏輯思維的基本形式。
在尺規作圖的細致操作和嚴謹證明中,學生還能深刻體會到尺規作圖的簡潔美、精確美、嚴謹美,這些都是數學獨有的文化魅力。通過這樣的學習既達成了數學教育的學科價值目標,更凸顯數學教育中獨特的育人價值追求,有助于學生數學學科核心素養的形成[3]。
三、尺規作圖教學路徑新視角
1.歷史視角:挖掘幾何知識的發生背景
尺規作圖是幾何作圖中最基本的形式之一,是培養小學生演繹推理數學思維的載體。在歐式幾何的代表作《幾何原本》中給出了許多數學家尺規作圖的方法。新修訂課標中提到的小學階段對尺規作圖的要求在這本著作中都能找到對應的思想原點和發生背景。所以,在整體梳理、追本溯源中能讓學生更清楚地知曉幾何知識發生、發展的歷史脈絡,感悟尺規作圖這種演繹推理的重要數學思想精髓,為學生當下的作圖學習提供依據和原理。表2是新修訂課標中的尺規作圖教學內容與《幾何原本》中相對應的出處及表述。
通過梳理尺規作圖教學內容,我們可以發現一些重要的幾何基本事實在小學數學教材中都有相關的孕伏滲透。所以,教學中教師要用高觀點視角整體把握“尺規作圖”內容,引領學生追溯知識發生的原點,在手腦參與的做數學中獲得豐富的數學作圖經驗和深刻的幾何事實感悟,這些積淀有助于學生空間觀念的提升。
2.思維視角:孕育數學理性的思維光芒
數學家克萊因說過:“數學是一種理性的精神,使人類的思維得以運用到最完善的程度。”小學階段的尺規作圖讓學生從直觀經驗過渡到操作實驗,再進一步發展提升到推理論證的邏輯思維層面,科學合理地讓學生經歷具象經驗到抽象思維的邏輯遞升過程,既有正向的合情推理思考,又有逆向的演繹推理思辨,真正在操作中進行思考和提升,助力學生數學核心素養的培養[4]。如在四年級認識三角形之后,安排了“三角形三邊關系”的探究學習。
【常規設計】
教師提供一組結構化的學具材料(如小棒或吸管等),引導學生任選其中的三根,動手圍成三角形。
提出問題:任選三根小棒,都能圍成一個三角形嗎?
實驗工具:四種長度不同的小棒、實驗記錄單。
實驗方法:圍一圍、比一比、算一算。
實驗要求:
(1)選一選:任選三根小棒,動手圍成一個三角形。
(2)比一比:哪些小棒能圍成三角形?哪些小棒不能圍成三角形?
(3)想一想:為什么有的小棒不能圍成三角形?而有的小棒能圍成三角形?
學生利用這樣的實驗素材操作時,常常會因為小棒本身的粗細問題或操作過程中的實驗誤差等因素,導致兩條短邊之和等于第三邊時,卻出現能圍成三角形的尷尬。
【尺規作圖新設計】
教師在學生已經知道“兩點之間線段最短”的基礎上,先讓學生猜想三角形中三邊存在怎樣的關系,再利用上述結論初步感知三邊關系;然后判定怎樣的三邊能圍成三角形,借助尺規作圖動手作出符合要求的三角形,在動手操作中讓學生發現并驗證猜想,從而發現規律存在的必要條件。
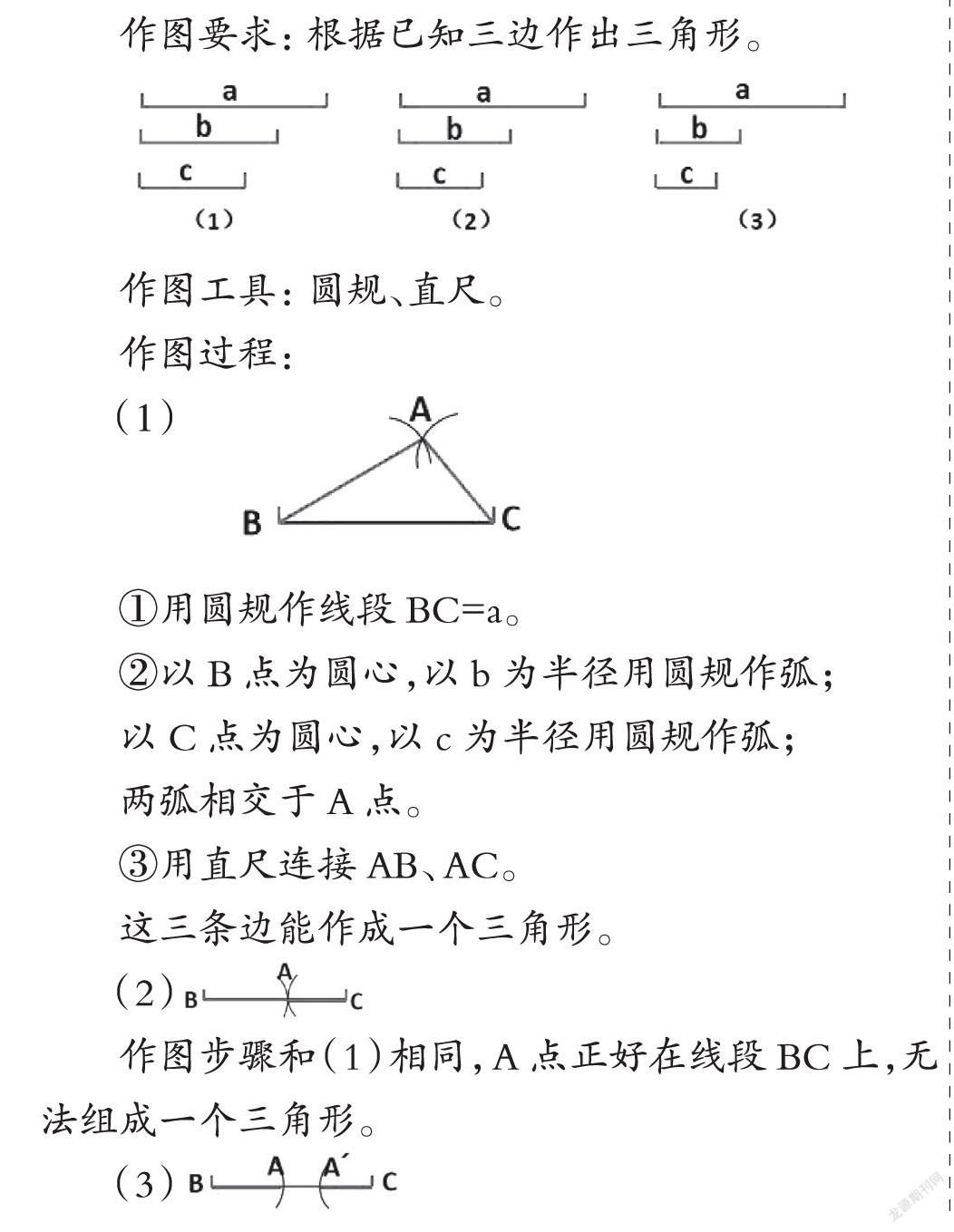
作圖要求:根據已知三邊作出三角形。
作圖工具:圓規、直尺。
作圖過程:
(1)
①用圓規作線段BC=a。
②以B點為圓心,以b為半徑用圓規作弧;
以C點為圓心,以c為半徑用圓規作弧;
兩弧相交于A點。
③用直尺連接AB、AC。
這三條邊能作成一個三角形。
(2)
作圖步驟和(1)相同,A點正好在線段BC上,無法組成一個三角形。
(3)
作圖步驟和(1)相同,A點和A′點沒有重合,無法組成一個三角形。
作圖思考:什么情況下三條邊一定能作出三角形?什么情況下不能作出三角形?
學生在這樣的尺規作圖中能精準發現,第(2)、第(3)種情況,即兩邊之和等于或小于第三邊時,無法作出三角形。在動手操作作圖中,不僅很好地驗證了開始的猜想,而且還避免了因實驗工具誤差所產生的干擾和不確定性。科學、精準、理性地提升學生的空間想象力和思維嚴謹性,用尺規作圖驗證了數學中三角形三邊關系的重要定理。
3.發生學視角:深化幾何學的育人價值
幾何學是研究形的科學,以人的視覺思維為主導,旨在培養人的觀察能力、空間想象能力和洞察力。尺規作圖是建立在幾何推理基礎上的一種作圖方法,學生在動手作圖過程中,除了從幾何知識的源頭了解其發生、發展過程,感受幾何學發展對人們日常生活、科技進步、社會發展帶來的巨大變化,更要從中感受到幾何作圖外在形式的結構美、邏輯推理的嚴謹美、精準表達的簡潔美、精確刻畫的細致美等,同時在廣泛的數學應用中感受它的應用價值,激發學生深入研究的興趣和動力。
綜上,教師應充分挖掘“圖形與幾何”中尺規作圖的教育價值,選取具有學科核心要素、本質特征、育人價值的素材作為課程資源,設計尺規作圖教學活動。在學習領悟幾何學本質內涵的同時,更好地感受人文精神、科學素養、道德品質等方面的熏陶,將學科育人的價值目標真正落實到教學中,促進學科知識向學科素養的生動轉化。
參考文獻
[1] 中華人民共和國教育部.義務教育數學課程標準(2011年版)[S].北京:北京師范大學出版社,2012,1.
[2] 曹培英.跨越斷層,走出誤區:小學數學課程新增內容及其教學的實踐研究(四)[J].小學數學教師,2020(10):4-13.
[3] 郭元祥.論學科育人的邏輯起點、內在條件與實踐訴求[J].教育研究,2020(04):4-15.
[4] 袁國超.基于核心素養的深度學習實現路徑[J].江蘇教育研究,2019(11):4-8.
[責任編輯:陳國慶]
3188501908281

