基于APOS理論的初中數(shù)學概念教學實踐初探

徐明敏

[摘 ?要] APOS理論是一種關于數(shù)學概念教學的建構主義理論. 通過對APOS理論的理解和研究，筆者基于APOS理論設計了一次“直線和圓的位置關系”的概念教學實踐，分析和探討了初中學生在APOS理論四個階段體現(xiàn)的對數(shù)學概念的理解情況，期待APOS理論在數(shù)學概念教學實踐中能有效地提升教學效率.

[關鍵詞] APOS理論;教學模式;數(shù)學概念;理解情況

前言

APOS理論是在20世紀80年代末至90年代初由美國數(shù)學家杜賓塞斯（Dubinsky）等人在數(shù)學教育研究實踐中發(fā)展起來的一種數(shù)學教學理論. APOS理論是一種關于數(shù)學概念教學的建構主義理論，該理論強調(diào)教學過程中應將數(shù)學概念與現(xiàn)實社會中的實例相結合，學生通過自身的經(jīng)驗，將兩者聯(lián)系起來，讓學生經(jīng)歷數(shù)學概念的形成過程. APOS理論將數(shù)學概念形成過程分為以下循序漸進的四個階段：操作或活動階段（Action）、過程階段（Process）、對象階段（Object）、模型階段（Schema）. 其中，“操作或活動階段”指學生通過一系列外顯的數(shù)學探究活動去獲得概念的內(nèi)隱本質(zhì)的過程;“過程階段”是“操作或活動階段”的內(nèi)化和提升，即學生通過對外顯的數(shù)學探究活動的進一步思考，抽象出概念的本質(zhì)特征，將新概念納入自己的認知結構;“對象階段”是給抽象出的概念的本質(zhì)特征賦予形式化的定義和符號，使其成為一個具體的對象;“模型階段”是學生知識積累的發(fā)揮階段，將新概念與其他概念建立聯(lián)系，形成知識的綜合模型，將這個模型納入自身的認知結構，與已有知識建立新的實質(zhì)性聯(lián)系. 在這四個階段完成過程中，學生的認知結構在不斷地進行調(diào)整，使自己不斷加深對數(shù)學概念的理解，學生的認知水平也會由此上升到更高層次.

通過對APOS理論的理解和研究，筆者基于APOS理論設計了一次“直線和圓的位置關系”的概念教學實踐，分析和探討了初中學生在APOS理論四個階段體現(xiàn)的對數(shù)學概念的理解情況，讓筆者深有感觸，由此以本文章展現(xiàn)出來，期望對初中數(shù)學教師設計概念教學模式有所幫助.

基于APOS理論的初中數(shù)學概

念教學模式的實踐過程

1. 操作或活動階段

“操作或活動階段”是學生通過一系列外顯的數(shù)學探究活動去獲得概念的內(nèi)隱本質(zhì)的過程，雖說“外顯的數(shù)學探究活動”是該階段學生獲得概念的內(nèi)隱本質(zhì)的關鍵所在，但是其中的“外顯”容易讓人誤會“探究活動”只是具體實體的動手表象活動，使得不少教師對課程使用的工具和時間的安排容易產(chǎn)生困惑和煩惱，這在一定程度上會讓教師本身對課程失去興趣和控制. 其實，“外顯的數(shù)學探究活動”還包括一些“抽象的經(jīng)驗或知識”對學習對象內(nèi)隱本質(zhì)的顯現(xiàn).

環(huán)節(jié)1 ?溫故知新.

回顧1：點和圓的位置關系有_____種. 如圖1所示，如果⊙O的半徑為r：①點P在圓_____，OP_____r;②點P在圓______，OP______r;③點P在圓______，OP______r.

回顧2：如圖2所示，已知AB=4 cm：①以A為圓心，5 cm為半徑畫圓，點B在圓_____;②以A為圓心，4 cm為半徑畫圓，點B在圓____;③以A為圓心，3 cm為半徑畫圓，點B在圓____.

設計說明 ?對“點和圓的位置關系”的溫故知新，是對上位概念的回味，由回味對知識進行遷移，點和圓的三種位置關系對后面類比教學“直線和圓的位置關系”埋下了伏筆. 在回顧1和回顧2中，讓學生明白除了用“形”之外，還可以用“數(shù)”來判斷位置關系，這不僅滲透了轉(zhuǎn)化與化歸思想，而且讓學生深刻體會了數(shù)形結合思想的應用.

2. 過程階段

“過程階段”是“操作或活動階段”的內(nèi)化和提升，在課程中讓學生明白僅以“形”來判斷位置關系是模糊的，應加以數(shù)量關系進行判斷更具嚴謹性和科學性，將這樣新的研究意識納入學生的認知系統(tǒng)中. 不僅如此，在過程中通過觀察、實驗、討論、合作等數(shù)學活動的開展，可使學生更加熟悉探究和創(chuàng)造，逐步了解探索、解決問題的一般方法——類比、轉(zhuǎn)化等.

環(huán)節(jié)2 ?類比、轉(zhuǎn)化.

探究1：如果把“點”換成“直線”，直線和圓的位置關系有哪些？你能夠借此在紙上畫出來嗎？（學生繪畫后可以利用動畫演示圖片）

探究2：你畫的圖有公共點嗎？有幾個？

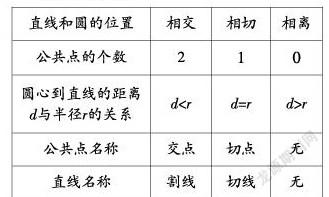
探究3：如果⊙O的半徑為r，圓心到直線的距離為d，類比兩者的大小：①直線和圓相交？圳d____r，直線與圓有____個公共點;②直線和圓相切？圳d____r，直線與圓有____個公共點;③直線和圓相離？圳d____r，直線與圓有____個公共點.

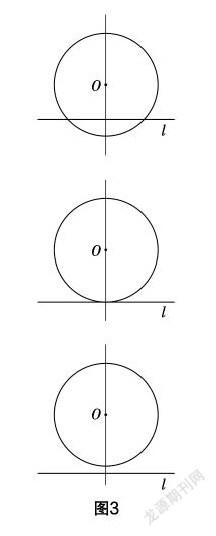
探究4：判斷下列直線和圓的位置關系（如圖3所示）.

設計說明 ?由于學生對“點和圓的位置關系”的理解和掌握，知識的正遷移可以讓學生以點在圓內(nèi)、圓上、圓外類比到直線和圓的三種位置關系——相交、相切、相離，并與相應的公共點的個數(shù)相接連;但是當直線和圓相交太近時，學生無法從“形”的角度對直線和圓相交的公共點的個數(shù)進行判斷（如圖3所示），讓學生開始明白除去用“形”之外，更加嚴謹和科學的是用“數(shù)”來判斷直線和圓的位置關系，這對后面用數(shù)量關系來判斷位置關系做下了鋪墊.

3. 對象階段

“對象階段”是給抽象出的概念的本質(zhì)特征賦予形式化的定義和符號，使其成為一個具體的對象. 在“直線和圓的位置關系”的教學中，“對象階段”主要進行的就是，學生在了解了直線和圓的三種位置關系的定義后，從數(shù)量關系的角度去研究直線和圓的三種位置關系. 在這個階段，學生會將動態(tài)的直線和圓的位置關系轉(zhuǎn)變成靜態(tài)的、整體的結構關系——圓的半徑r（或直徑）與圓心到直線的距離d的數(shù)量關系？圳直線和圓的公共點的個數(shù)？圳直線和圓的位置關系.

環(huán)節(jié)3 ?用數(shù)量關系判斷位置關系.

問題1：如果現(xiàn)在已知圖3中圓的直徑是15 mm，圓心到直線的距離分別是7.49 mm，7.50 mm，7.51 mm，那么圖3中直線和圓分別是什么位置關系？它們各有幾個公共點？

問題2：已知圓的半徑為4，設圓心到直線的距離為d，如果直線和圓相交，那么d的取值范圍是_______;如果直線和圓相切，那么d的取值范圍是________;如果直線和圓相離，那么d的取值范圍是______.

問題3：如圖4所示，點A是一個半徑為300 m的圓形森林公園的中心，在森林公園附近有B，C兩個村莊，現(xiàn)要在B，C兩村莊之間修一條長為1000 m的筆直公路將兩村連通.經(jīng)測量，得∠ABC=45°，∠ACB=30°，問：此公路是否會穿過該森林公園？請經(jīng)過計算說明.

設計說明 ?利用圓心和直線的數(shù)量關系（距離和半徑）來判斷直線和圓的位置關系，是學生學習直線和圓的位置關系的性質(zhì)與判定的階梯，加強了學生“數(shù)”“形”相互轉(zhuǎn)化的意識和應用，讓學生理解判斷直線和圓的位置關系為什么要轉(zhuǎn)化成圓心到直線的距離和圓的半徑的大小關系來實現(xiàn).

4. 模型階段

“模型階段”是學生知識積累的發(fā)揮階段，將新概念與其他概念建立聯(lián)系，形成知識的綜合模型. 可以說，模型階段是學生知識總結和拓展階段，通過持續(xù)聯(lián)系、加工和深化，會使學生對新學的數(shù)學概念的理解不斷加深，學生的思維和認知水平也會上升到更高水平和更高層次.

環(huán)節(jié)4 ?總結和拓展.

總結：使用數(shù)據(jù)來判斷直線和圓的三種位置關系：

拓展1：直線l與⊙O相切于點A，直徑AB與直線l有怎樣的位置關系？

拓展2：圓心到直線的距離如何計算？有哪些方法？

拓展3：直線和圓的公共點的個數(shù)與二次函數(shù)有什么聯(lián)系？

設計說明 ?通過填表的方式引導學生進行總結，回顧本節(jié)課所學的主要知識，幫助學生養(yǎng)成總結的好習慣;拓展的內(nèi)容比較適合學生課后自主探索，通過探索讓學生體會知識之間的聯(lián)系，更容易加深和完善學生對認知結構的建立，這對后期的學習打下了基礎.

思考

從APOS理論可以看出，數(shù)學概念教學模式的實踐是循序漸進的概念建構過程，在整個過程中，每個階段都缺一不可. 相應的教學活動在整個過程中或許有些不同，但每個階段都自有成立的關鍵之處. 在“操作或活動階段”，外顯的數(shù)學探究活動需是學生能夠親身感知、有興趣去思考的教學活動，在活動中能體驗出概念的內(nèi)隱本質(zhì)，這是活動設計的關鍵. 在“過程階段”，要讓學生從直觀轉(zhuǎn)化到抽象，再從抽象轉(zhuǎn)化到對象，這既是過程階段的教學步驟，也是教學指向. 在“對象階段”，是師生忙碌一陣后看到結果顯示的重要時間，無論結果是大或者小，是多或者少，對每位學生來說，都應該熟悉和體驗到自己的收獲. 在“模型階段”，知識的綜合模型并不是此段學習內(nèi)容的終點，它是某個層次和更高層次的樞紐，這樣的意識是師生都應該具有的.

APOS理論是一種教學理論，更加適合數(shù)學概念教學，期望有更多教師能夠了解它、研究它，得出更多的使用它的策略.

3644501908223