受損懸索對稱性破缺下非線性耦合振動研究1)

趙珧冰 鄭攀攀 陳林聰 康厚軍

* (華僑大學土木工程學院,福建廈門 361021)

? (福建省智慧基礎設施與監測重點實驗室,福建廈門 361021)

** (廣西大學工程力學研究中心,南寧 530004)

引言

普遍存在于自然界中的對稱性,不僅是現代物理學的一個核心概念,而且從分子結構到自然景觀,從藝術作品到建筑結構,甚至詩詞歌賦,對稱性也處處體現.振動理論具有統一、簡潔、整齊、對稱和奇異等5 大美學特征[1],當中蘊含的美,一方面具有客觀存在性,同時對其認識亦存在相對性.對稱讓一切均衡有序,結構固有的對稱性,不但可以大幅降低動力學建模和分析計算工作量,還可以帶來視覺上沖擊和美感.近年來隨著奇異性理論和分岔理論等不斷發展,對于結構遭遇對稱性破缺[2]或非齊次邊界條件等問題[3],一些奇異性現象逐漸被人們認識和理解.由此可見對稱性及其破缺是結構振動分析中不可忽視的關鍵因素.

以工程中常見的索結構為例[4],兩端水平自由懸掛的索具有明顯的結構對稱性.但是這種對稱性很容易被打破,比如:端點不在同一水平位置的斜拉索[5];包含非均勻分布的集中質量[6];存在非均勻損傷[7]等.因此一旦索結構遭遇到對稱性破缺,系統固有特性將或多或少發生改變,比如頻率[8-10].具體而言,水平懸索固有頻率隨著Irvine 參數[11]增大,會出現多個交點,該處固有頻率相等.對于斜拉索,由于對稱性破缺,頻率間交點消失,從而出現轉向點.此時隨著Irvine 參數不斷增大,兩固有頻率會不斷接近然后迅速分開[12].對于各類動力系統或結構,當其固有頻率相等或近似相等時,系統有可能會出現明顯的模態耦合共振[13-17],能量會在模態間發生傳遞,導致系統產生更為復雜的動力學現象.已有研究表明[18-19]:對于懸索/斜拉索,兩者會呈現出截然不同的模態耦合共振響應.由此可見,頻率交點/轉向點附近的動力學現象豐富且復雜,倘若進一步考慮系統對稱性破缺,其動力學特性將發生更多定性和定量的改變.

索是一類典型的易損構件[20-22],不對稱損傷是引發系統對稱性破缺的重要因素之一.對于受損拉索,Jiang 等[23]建立考慮鋼絲磨損和索內腐蝕分布的斜拉索的腐蝕疲勞模型,分析了不同環境條件中拉索的腐蝕疲勞.Bouaanani[24]采用有限差分法研究損傷位置和范圍對懸索模態靈敏度影響,研究不同損傷情況下懸索的力學特性.Lepidi[25]基于受損懸索力學模型,以面內頻率為損傷指標,識別懸索損傷.Sun 等[26]建立了腐蝕拉索靜力學模型和平面內自由振動的控制方程,分析表明隨著腐蝕時間增加,拉索張力、垂度和固有頻率將出現明顯變化.Xu 等[27]基于損傷拉索的微觀力學模型,提出了一種斷絲拉索靜、動力特性的分析方法,考慮不同物理參數,分析斷絲損傷對拉索靜動力特性影響.王立彬等[28]通過推導拉索損傷后的索力和線形公式來分析損傷拉索的等效彈性模量.蘭成明等[29]對已經服役18 年的拉索鋼絲開展研究,發現拉索腐蝕鋼絲的屈服強度和極限應變都有所降低,腐蝕鋼絲與未腐蝕鋼絲的彈性模量基本相同.Zhu 等[30]采用同倫分析法研究斜拉梁中拉索受損后,該系統的動力學行為.

上述研究主要關注拉索疲勞或腐蝕損傷的機理,或分析損傷后的頻率、振型和索力等.對于受損懸索,經典的對稱拋物線構形已無法準確刻畫對稱性破缺后的分段構形.因此如何采用分段函數擬合受損系統的懸鏈線構形?如何進一步從非線性動力學的角度去分析受損懸索的動力學行為?尤其是對稱性破缺導致頻率間交點變為轉向點后,受損系統多模態間的耦合共振響應特性又會發生哪些定量和定性的變化?這些問題值得進一步探索和研究.

本文基于受損懸索面內非線性動力學模型,采用分段樣條曲線描述損傷后的靜態構形,并利用多尺度法得到模態耦合共振的調諧方程.通過數值算例,探究受損懸索對稱性破缺下的耦合振動特性.

1 數學模型

假定懸索由均勻、連續的彈性材料構成,且只考慮索橫截面上均勻分布的拉應力和拉應變,忽略剪切、抗彎和扭轉剛度.損傷懸索無應力狀態下的構形如圖1 左圖所示,采用弧坐標s 貫穿懸索全長,EA 表示軸向剛度,EAd(s)表示受損后殘余軸向剛度.假設銹蝕部分的殘余截面面積相等,損傷區域為[a1,a2],不對稱分布.L0為無應力狀態下索長,L 表示水平跨度,bd表示受損懸索的垂度.無損和受損的懸索的靜態、動態構形如圖1 右圖所示,u(x,t) 和v(x,t)分別表示軸向和豎向的位移分量.

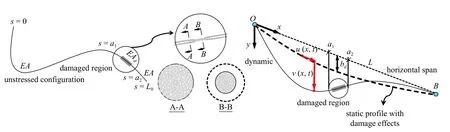
圖1 受損懸索構形及特性Fig.1 Configurations and characteristics of the damaged suspended cable

引入以下3 個無量綱參數分別描述懸索損傷的程度、范圍和位置[7]

損傷程度在整個索長上變化用分段函數表示

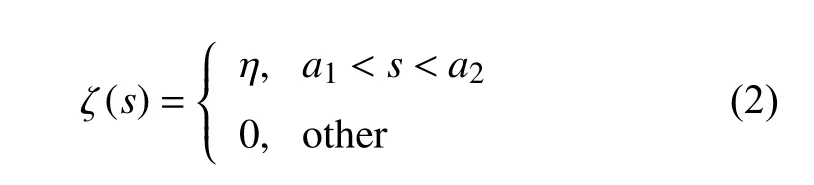
損傷會導致懸索形成新的靜力構形,引起張力減小,垂度增大.因此本文引入懸索水平張力折減系數χ2和垂度增大系數 κ2[7]:Hd=χ2H,bd=κ2b.式中Hd(H)分別表示受損(無損)懸索的初始水平張力,通過求解其靜力學平衡方程得到.

損傷會改變水平懸索的靜態構形,倘若損傷呈現出明顯不對稱性,此時拋物線就無法準確描述受損后的靜態構形,因此需要采用分段樣條曲線來擬合[7].節點之間每段曲線都由一個多項式函數yj(x)映射.比如對于一段受損懸索的線形,可以采用三段拋物線近似表示:未損段y1(x) (0＜x＜a1),受損段y2(x)(a1＜x＜a2),未損段y3(x) (a2＜x＜L),此時節點處需滿足連續性條件

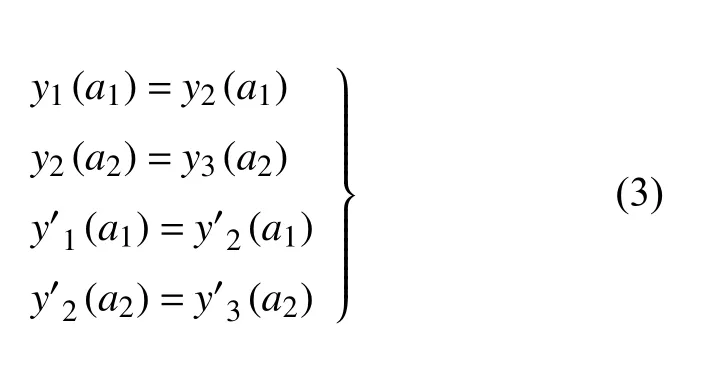
利用哈密頓變分原理,可得懸索面內非線性運動微分方程

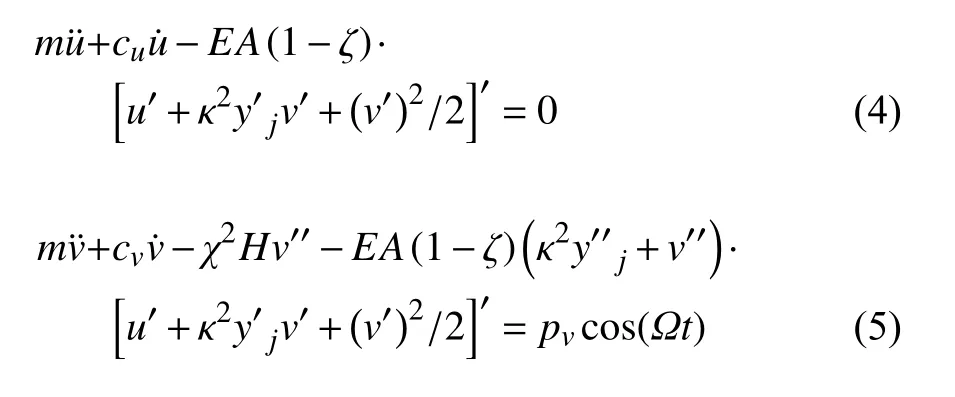
式中,點表示對t 求導,撇表示對x 求導,m 和cv,cu分別為單位長度質量和阻尼系數,pv和Ω 為外激勵幅值和頻率.

系統的邊界條件和連續條件表示為

因此受損懸索面內運動方程可以簡化為

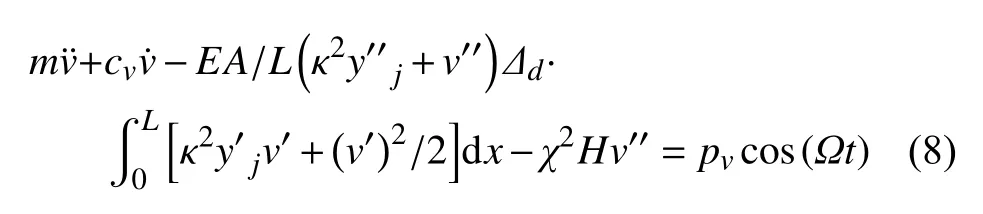
引入以下無量綱參數

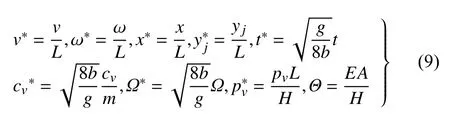
可得無量綱化后的運動方程

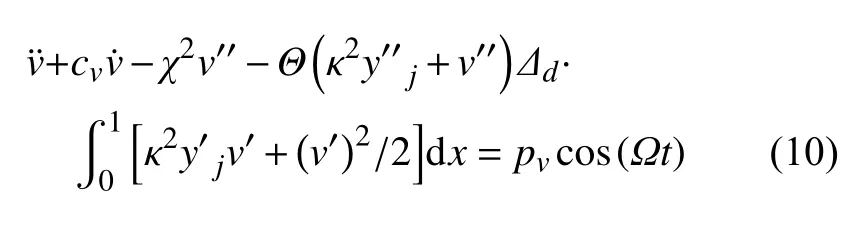
采用分離變量法:v(x,t)=eiωtφ(x),忽略非線性項、阻尼項和激勵項等,通過線性化處理,可得

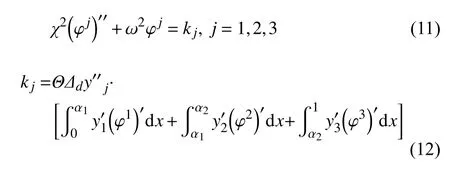
式中α1=a1/L,α2=a2/L.可知特征函數的分段解為

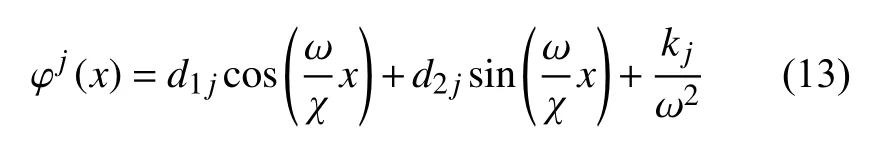
模態函數的邊界條件和連續性如下

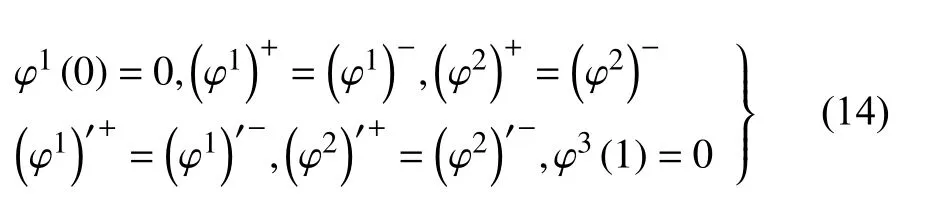
將式(13)代入式(12),并將邊界條件代入式(13),可得由未知系數d1j,d2j和特征頻率ω 組成的7 × 7系數矩陣.

利用Galerkin 法對式(10)進行離散

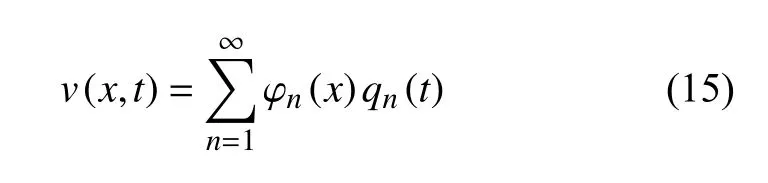
其中 φn(x) 表示模態函數,qn(t) 為坐標函數.

將式(15)代入式(10),兩邊同時乘以 φn(x) 后從0 到L 積分,可得離散的無窮維方程

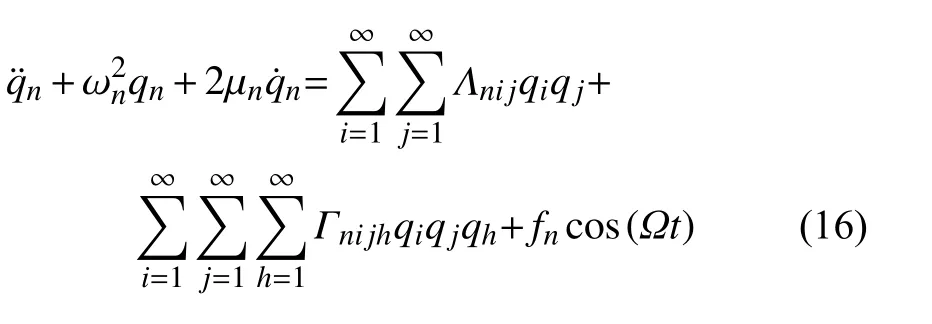
其中各項系數表達式如附錄A 所示.

2 攝動分析

首先將二階微分方程(16)改寫為

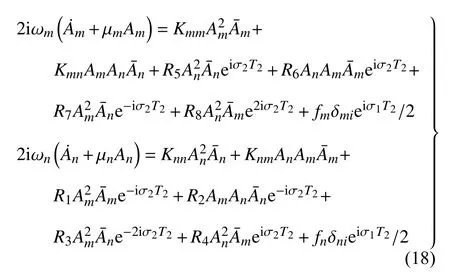
其中非線性系數Kij見附錄B,2K1=R2=2R4=2R5,2K2=R6=2R1=2R7,K3=R3=R8.將Aj表示為直角坐標形式:Aj=代入式(18)可得

3 數值算例與分析

3.1 靜態構形、頻率及模態

懸索物理參數為:L=200.0 m,A=7.069 × 10-2m2,E=200 GPa 以及ρ=7800.0 kg/m3.無量綱化后的阻尼系數分別為:μm=0.005,μn=0.006.不對稱的損傷參數為:損傷程度η=0.4、損傷范圍δ=0.3、損傷位置α=0.7.對于無損系統,其構形可以采用拋物線描述y(x)=(-4x2+4x)f.一旦遭遇非對稱損傷,此時對稱性破缺,需要采用樣條曲線擬合受損懸索的懸鏈線構形.經擬合,可以得到以下分段函數

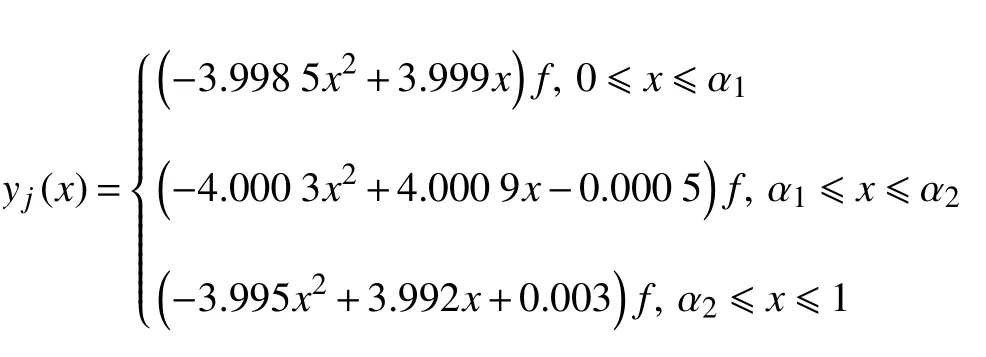
對比上述兩組方程,由于非對稱損傷導致懸索構形函數發生改變,用分段樣條曲線表示的線形將不再具有對稱性.因此本文將重點分析和討論對稱性破缺的動力系統,其線性和非線性振動特性.

首先,圖2 給出了無損和受損懸索前六階模態頻率ω/π 和Irvine 參數λ2的關系曲線.如圖2(a)所示,對于無損結構,其模態頻率分為正對稱和反對稱兩類,且隨著Irvine 參數的不斷增大,系統頻率之間存在多個交點.觀察圖2(b)可知:懸索發生不對稱損傷后,系統模態頻率之間交點將消失,其頻率軌跡會相互接近,然后迅速分開,形成頻率轉向點.此時各階頻率ω 包含在7 × 7 的系數矩陣中,如附錄C所示.

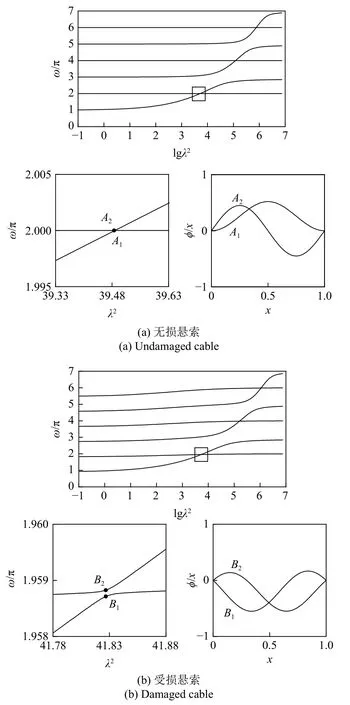
圖2 懸索模態頻率和Irvine 參數關系曲線及其模態振型Fig.2 Relationship curves between Irvine parameter and mode frequencies and shapes

值得一提的是,此時由于模態振型不再嚴格區分正、反對稱形式,因此轉向點附近模態振型失去了對稱性.針對《公路橋梁抗風設計規范》(JTG/T 3360-01-2018)中對于斜拉索頻率面內頻率計算,如果嚴格從力學概念而言,斜拉索和受損的水平懸索,由于系統存在對稱性破缺,其頻率和模態不宜再分為正、反對稱兩類形式.

3.2 激勵響應幅值曲線/幅頻響應曲線

表1 給出了無損和受損懸索的參數以及非線性相互作用系數.當系統的兩個模態頻率接近時,在外激勵作用下,能量將在不同模態間傳遞,導致系統發生1:1 內共振.由表1 數據可知:由于無損懸索具有對稱性,假設高階為正對稱模態,低階為反對稱模態,可得非線性相互作用系數K1=K2=0.而損傷懸索由于其模態振型對稱性破缺,此時K1≠0 和K2≠0.表1中部分參數正負號也出現了截然相反的情況,由此可見對稱性破缺后,隨著非線性相互作用系數的改變,系統非線性耦合動力學行為也發生變化.此外損傷后懸索的頻率呈現出明顯下降的趨勢,這一特點與溫度效應有所區別.

表1 無損和受損懸索的參數與非線性相互作用系數Table 1 Parameters and nonlinear interaction coefficients of undamaged and damaged suspended cables

對于激勵直接作用于高階(Ω≈ω2),圖3 給出了無損和受損懸索的激勵響應幅值曲線.其中實線為穩定解,虛線為不穩定解,SN 和HB 分別表示鞍節點分岔和霍普夫分岔.如圖3(a)所示,對于無損懸索,穩態解可以明顯分為兩類:單模態解和雙模態解(內共振).對于前者(a1=0),隨著外激勵幅值f2不斷增加,直接激勵響應幅值a2不斷增大.選取合適的初始條件,可以得到第二類內共振解.此時由于內共振而激發的低階模態響應幅值a1明顯要大于a2.且隨著f2不斷減小,a1和a2逐漸降低,直到SN1,系統發生跳躍現象,此處a2迅速增大,a1則直接變成0,系統再次出現單模態解.

圖3(b)給出了受損系統的激勵響應幅值曲線.此時系統不存在明顯的單模態解,隨著f2的增大,a2會不斷增加,直到0.000 8 附近,出現第一個鞍結點分岔SN1,發生跳躍現象.同時,a1也不斷增大,直到SN1.倘若f2進一步增加,此時a2不會一直增加,而會出現一段飽和現象直至第二個霍普夫分岔HB2,能量將不斷通過內共振的形式傳遞到低階模態,導致a1不斷增大.倘若f2從大不斷減小直到0,對于穩定解而言,a2由于飽和現象,會基本保持不變,a1則不斷減小,直到第3 個鞍結點分岔SN3,幅值發生明顯的跳躍現象,迅速下降.此外選擇合適的初始條件,可以得到鞍結點分岔SN2與霍普夫分岔HB1之間小范圍的穩定解.

如圖3 所示,對比無損和受損懸索的鞍結點分岔,懸索受損后,分岔數量增加到3 個,由此導致跳躍現象增多,系統響應幅值突然增大或減小變得更加頻繁,影響懸索的疲勞性質.進而有可能導致懸索損傷程度、范圍和位置的進一步擴展和增加,嚴重影響索結構安全.因此在索結構的施工、運營與維護階段,需要及時識別索的損傷,并及時采取相應措施進行處理,避免由于出現局部損傷后不斷加劇,最終導致整體結構安全受影響.

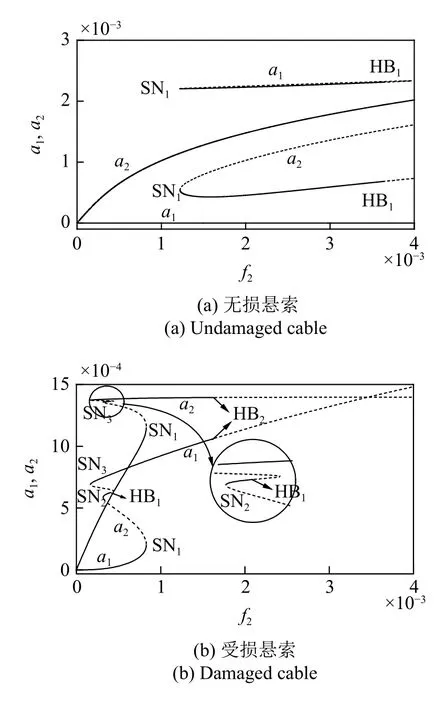
圖3 激勵響應幅值曲線 (f1=0,σ1=0.05 和σ2=0.2)Fig.3 Excitation response amplitude curves when f1=0,σ1=0.05 and σ2=0.2

選取外激勵幅值f2=0.002 以及內調諧參數σ2=0.2,圖4 描述了當外激勵直接作用于高階模態(Ω ≈ ω2)時,無損和受損懸索的幅頻響應曲線.其中實線和虛線分別為穩定和不穩定解,PF 為叉形分岔.

對于無損系統,如圖4(a)所示,與激勵響應幅值曲線類似,系統會呈現出明顯的單模態解和內共振解.此時可以觀察到兩個叉形分岔PF1和PF2.選擇一定的初始條件,系統會展現出明顯的耦合共振.當外調諧參數σ1的不斷增加時,a1和a2均會不斷減小,直到第一個霍普夫分岔HB1.此后系統出現不穩定解.倘若σ1繼續增加,系統會出現第二個霍普夫分岔HB2,此時系統重新出現穩定解.如果σ1仍然繼續增加,a1會呈現增大的趨勢,而a2基本不變.

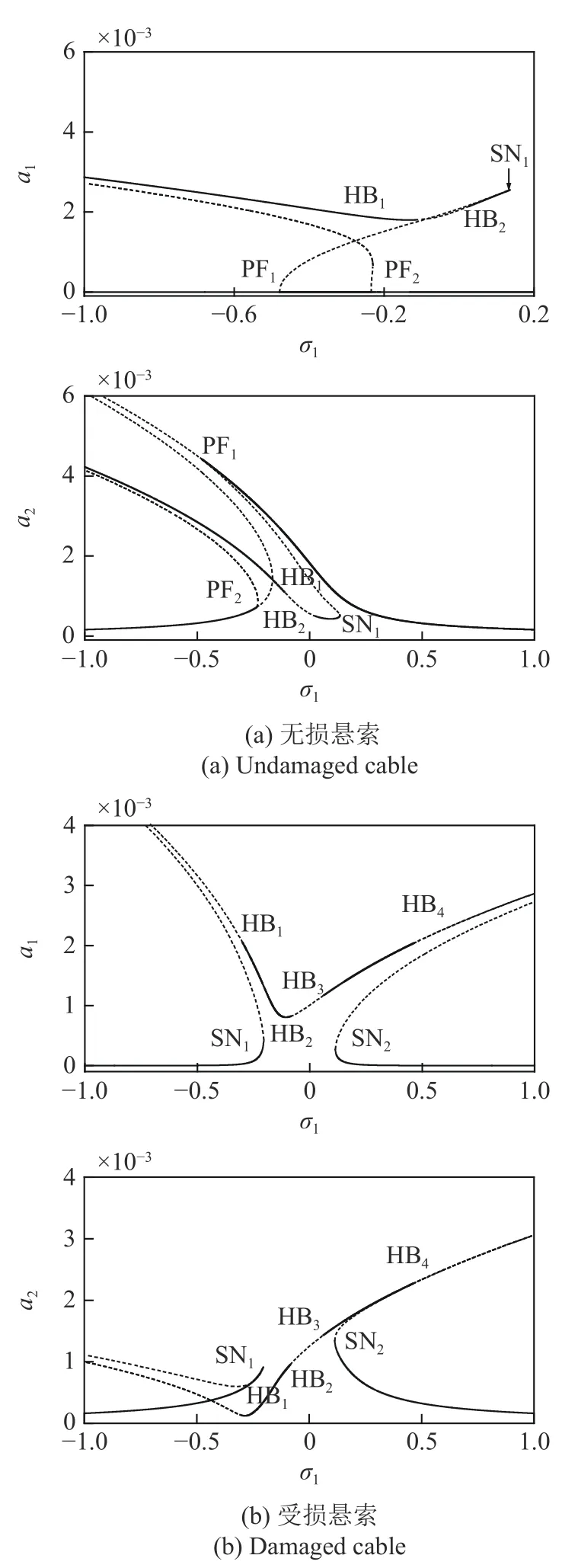
圖4 幅頻響應曲線 (f1=0,f2=0.002 和σ2=0.2)Fig.4 Frequency-response curves when f1=0,f2=0.002 and σ2=0.2

對于受損系統,其共振響應特性發生了顯著改變,如圖4(b)所示.隨著外調諧參數σ1從-1.0 開始不斷增大,對于穩定解,雖然內共振響應幅值a1雖小,但是其并不是恒等于零,且幅頻響應曲線中并沒有叉形分岔PF,而出現鞍結點分岔SN1,此處系統發生跳躍現象.對于系統的大幅振動,一開始為不穩定解,隨著調諧參數σ1不斷增大,直到第一個霍普夫分岔HB1,此時系統開始出現穩定解.之后隨著σ1繼續增大,與無損系統類似,系統會經歷兩個霍普夫分岔HB2和HB3,內共振響應幅值a1呈現出先減小后增大的趨勢.倘若σ1繼續增加,系統又將恢復穩定解,直到第4 個霍普夫分岔HB4.對比圖4(a)可知:無損系統此時會出現鞍結點分岔SN1,導致系統出現跳躍現象.由此可見,受損傷影響,在交點和轉向點附近,系統模態間的耦合振動特性存在明顯的定性和定量的區別.

3.3 分岔和混沌

圖3 和圖4 中,無論是無損還是受損懸索,都存在霍普夫分岔.由于系統的非線性動力學行為在霍普夫分岔附近會發生明顯的改變,因此分別采用打靶法和Floquet 理論求解霍普夫分岔點附近的動態解并判斷其穩定性.圖5 給出了受損系統在兩個霍普夫分岔HB2和HB3間的動態解,其中實心圓是穩定的,空心圓是不穩定的.顯然HB3是一個超臨界霍普夫分岔,HB1點首先出現穩定的周期解分支,隨著調諧參數σ1的減少,系統會出現倍周期分岔PD1,表明系統存在通往混沌的路徑.

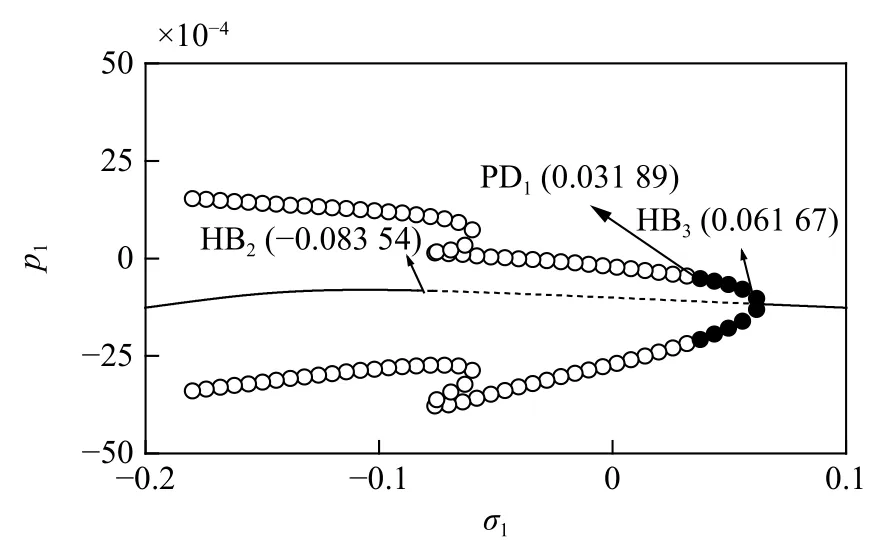
圖5 受損懸索霍普夫分岔點附近的動態解 (f1=0,f2=0.002 和σ2=0.2)Fig.5 Damaged suspended cable’s dynamic solutions around two Hopf bifurcations when f1=0,f2=0.002 and σ2=0.2

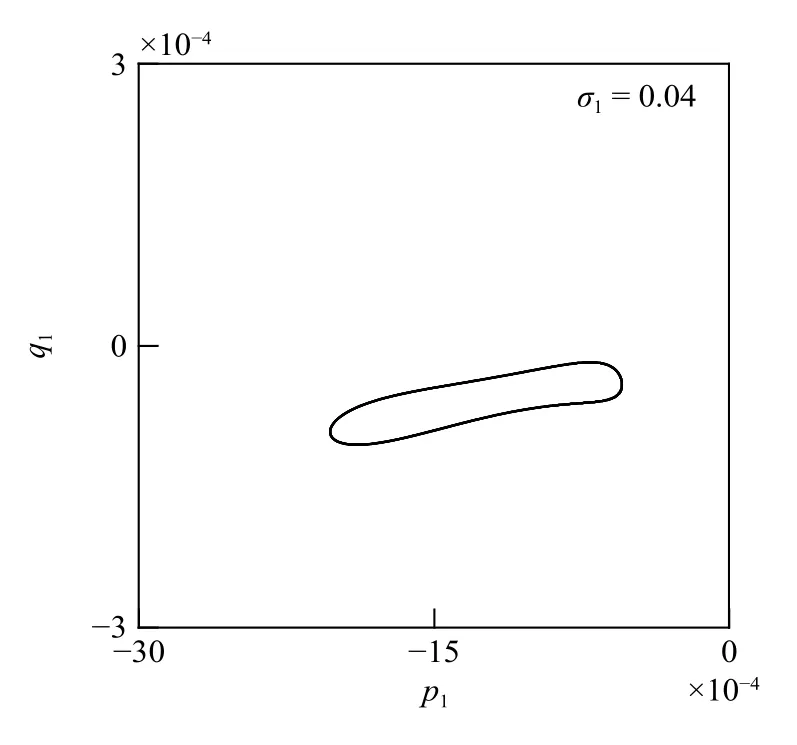
在PD1附近,外調諧參數σ1從0.04 不斷減小,依次選定為0.04→0.03→0.028→0.027 78→0.027 72,圖6 給出了系統在對應調諧參數變化時的相位圖.如圖所示,隨著調諧參數不斷增加,該動力系統會經歷周期1→2→4→8→···→混沌解.為了驗證系統出現的混沌運動,圖7 給出了系統的時程曲線、相位圖、頻率譜以及龐加萊截面,并計算出系統的最大李雅普諾夫指數.由時程曲線可以看出系統的波形呈現出明顯的隨機性,此時的龐加萊截面具有分形的特點,隨機性強.經計算可得其最大李雅普諾夫指數為0.003 57,據此可以判定為混沌吸引子.

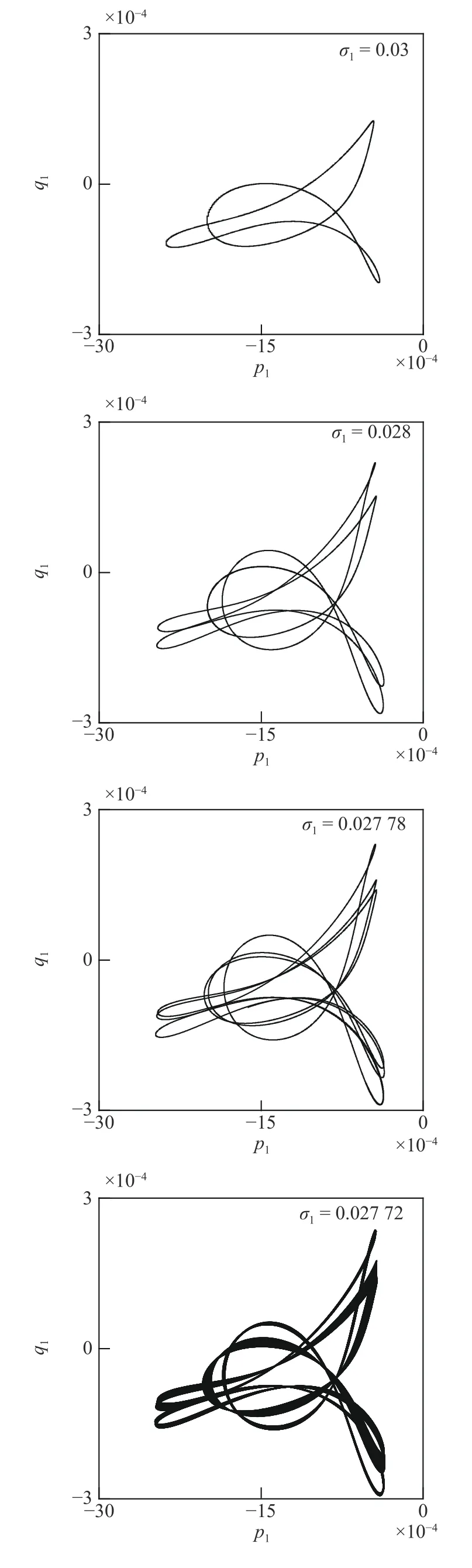
圖6 PD1 附近的相位圖:從周期解到混沌 (1→2→4→8→···→混沌)Fig.6 Phase portraits diagrams around PD1:from periodic motions to chaotic motions (1→2→4→8→···→chaos)

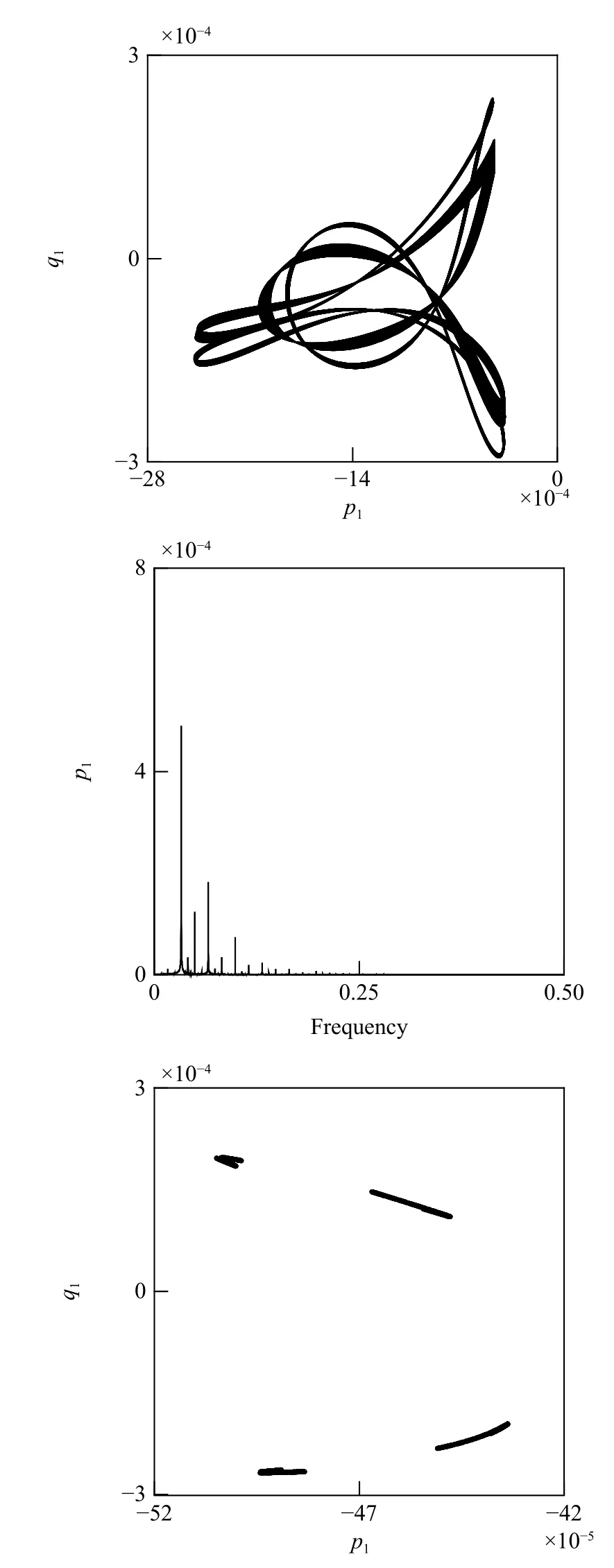
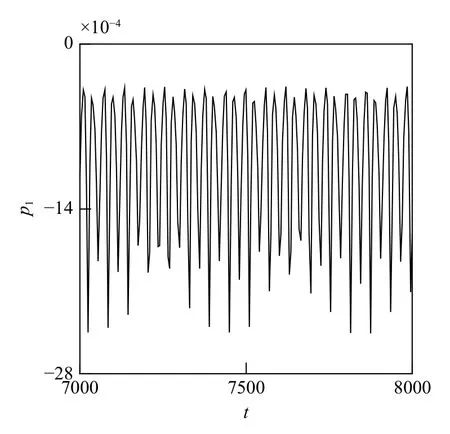
圖7 時程曲線、相位圖、頻譜以及龐加萊截面(f1=0,f2=0.002,σ1=0.027 72,σ2=0.2)Fig.7 Time history curves,phase portraits,frequency spectrums and Poincare sections when f1=0,f2=0.002,σ1=0.027 72,σ2=0.2

4 結論

水平懸索遭遇不對稱損傷后,其固有對稱性被打破,如果仍采用一段拋物線來描述受損后的線形,會出現細微差異.因此需采用樣條曲線擬合受損懸索的靜態構形,利用分段函數表示;由于損傷導致對稱性破缺,水平懸索固有頻率之間的交點變為轉向點,受損前正、反對稱模態也變為受損后的非對稱模態;失去對稱性后,受損系統非線性相互作用系數亦會產生明顯改變,導致其內共振響應產生顯著改變;當激勵直接作用在高階模態時,無損系統呈現出明顯的單模態解和多模態解(即內共振),但受損系統并沒有呈現出明顯的單模態解;損傷會導致系統的鞍結點分岔數量增加,導致系統可能發生的跳躍現象增多,引發響應幅值發生突變,影響索結構的疲勞性能;受損系統的分岔和混沌特性會發生明顯的改變,將通過倍周期分岔產生混沌運動.

附錄A

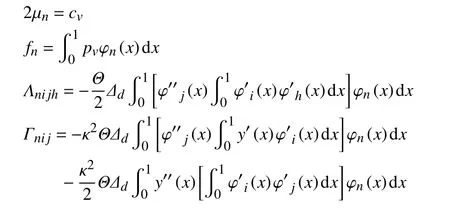
附錄B

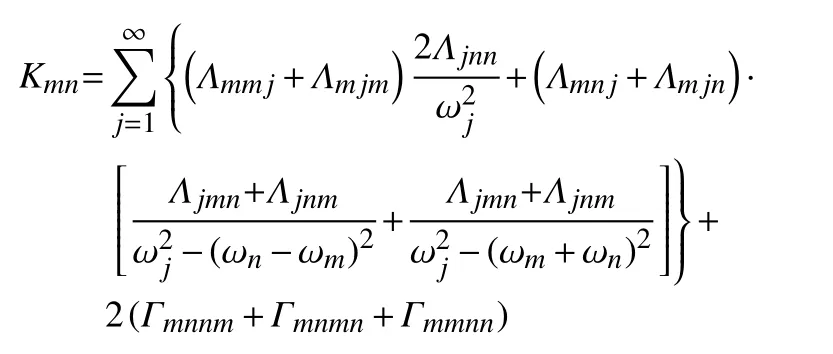
附錄C

7 × 7 系數矩陣中每個元素Aij分別表示為