初值約束與兩點邊值約束軌道動力學方程的快速數值計算方法1)

張 哲 代洪華 馮浩陽 汪雪川 岳曉奎

(西北工業大學航天學院,西安 710072)

(航天飛行動力學技術國家級重點實驗室,西安 710072)

引言

軌道快速計算是航天工程領域的基礎問題,廣泛存在于地球繞行軌道設計及深空探測等各種航天工程任務中,具有重要意義.軌道動力學問題在形式上一般描述為常微分方程初值問題或邊值問題,其中最具代表性的有軌道遞推問題[1-2]、攝動Lambert問題[3-4]和三體模型下的轉移軌道設計問題[5-6].軌道問題在早期一般通過微積分進行解析求解,牛頓與伯努利計算了萬有引力作用下的二體軌道解析解[7],歐拉與拉格朗日求出了限制性三體問題的5 個拉格朗日點[8].但當考慮更為一般的三體系統以至N 體系統時,解析求解將不再適用[9].龐加萊發展了漸進法并將其用于求解限制性三體問題,但由于三體問題具有混沌效應,其長期軌道仍然難以通過漸進法精確預測.此外,早期對軌道動力學問題的求解都是基于理想的均勻圓球或橢球模型,而在實際航天任務中則需要考慮地球非球形等擾動項,這些干擾力使得航天器軌道難以求得精確解析解.由于存在上述困難,在實際工程任務中,航天器軌道均采用數值方法進行求解.

軌道動力學問題最為經典的數值解法是有限差分類方法,其中代表性的包括Euler 法、Runge-Kutta法等[10].此類算法將待求解問題劃分為多個差分節點,逐點計算問題近似解.由于物理含義直觀且遞推方程較為簡單,有限差分法受到了廣泛關注,并在仿真軟件與科學計算函數中得到大量應用[11-12].然而,有限差分法的計算精度嚴重依賴于小步長,方法性能受到限制,在諸如航天器追逃博弈以及失效航天器快速在軌維修等任務中,將難以滿足任務實時性以及長期解算過程高效高精度的要求[13-14].

為克服有限差分法的原理性缺陷,學者們發展了一系列能實現大步長計算的迭代算法[15-21].1963年Clenshaw 與Norton[15]首次將Chebyshev 多項式與Picard 迭代法相結合,用于求解常微分方程的半解析解,該算法能夠避免有限差分法逐步計算的缺點,但其系數計算方案較為復雜,且僅適用于求解一維方程.其后,日本Fukushima[16]對Chebyshev 多項式與Picard 迭代法的結合方式予以改進,簡化了系數計算方案,并將求解對象拓展到高維常微分方程,但在這一改進方案中待解函數及其導數被分別估計,未能有效利用Chebyshev 多項式性質,引入的待定系數較多,計算量較大.此后,美國德州農工大學Bai[17]提出修正Chebyshev-Picard 迭代法(modified Chebyshev-Picard iteration method,MCPI),并將其用于求解軌道動力學問題,該算法利用Chebyshev多項式性質減少了待定系數,但由于在迭代公式推導中利用了反演公式,得到的迭代公式較為復雜,降低了算法效率.為進一步提高MCPI 算法計算效率,Woollands 等[18]對該算法進行改進,將導函數估計值與真實值之差作為迭代修正項,提高了算法收斂階,但引入了雅可比矩陣,增加了算法計算量.Wang 等[19]將變分迭代法與時域配點法相結合,提出了局部變分迭代法(local variational iteration method,LVIM),該算法將計算殘差用于誤差修正,結合時域配點法簡化了迭代公式推導過程,得到的計算公式較為簡潔,在軌道計算問題中收斂速度較快,但該算法由于對廣義拉格朗日乘子進行Taylor展開,同樣引入了雅可比矩陣,在求解復雜高維問題時產生的計算量過大.2020 年,Wang 等[20]將牛頓法與Picard 迭代法相結合,提出了多步Newton-Picard法(multistep Newton-Picard method,MNP),該算法將導數方程在待定函數真解處進行Taylor 展開,并依據展開式建立了一系列衍生算法,但Taylor 展開引入的偏微分算子使得算法迭代公式較為復雜,且算法收斂階較低.馮浩陽等[21]將局部變分迭代法、擬線性化法及疊加法相結合,提出了能用于求解邊值問題的擬線性化-局部變分迭代法,拓展了局部變分迭代法的適用范圍,但仍未能解決算法需要反復計算雅可比矩陣的弊端.

本文將誤差反饋機制與Picard 迭代法相結合,提出一種新的反饋迭代算法,避免對原函數進行泰勒展開,消除迭代公式中的雅可比矩陣,以保證計算效率;利用配點法與Chebyshev 多項式性質,將迭代公式推導中涉及的復雜符號運算轉化為線性代數運算,簡化推導過程,降低迭代公式的復雜度;結合擬線性化法與疊加法,拓展算法適用范圍,使之能夠求解兩點邊值問題;將變參數計算方案引入局部配點反饋迭代法,使算法能夠在運行過程中自適應選擇計算參數,進一步提高算法計算效率與計算精度,從而為在軌航天器的長期軌道快速預測提供一種高性能數值計算方法.

1 局部配點反饋迭代法

1.1 修正Chebyshev-Picard 迭代法

修正Chebyshev-Picard 迭代法是用于迭代求解常微分方程初值問題的數值算法[17],該算法求解常微分方程的具體過程簡述如下.

對于具有如下形式的一階常微分方程

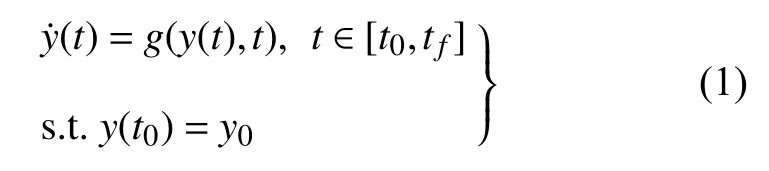
假設未知函數及其導數可以用正交多項式的線性組合來近似,即

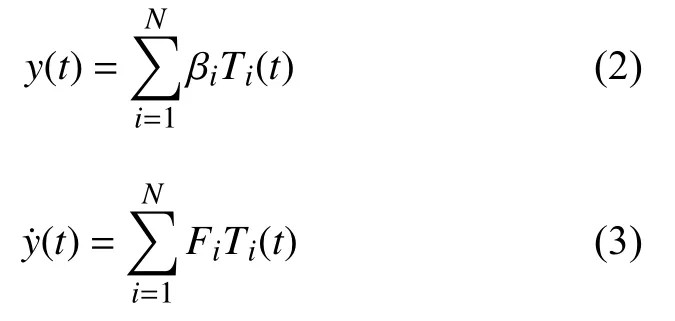
式中,Ti(t)為一組正交多項式組的第i 項,βi及Fi為Ti(t)的系數.

Picard 迭代法計算公式為

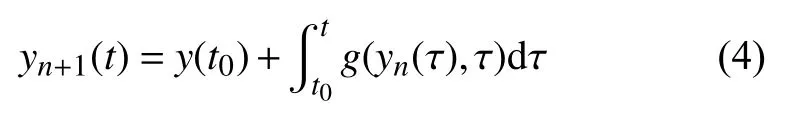
將式(2)與式(3)代入式(4),并令式(4)兩邊正交多項式對應項系數在一系列給定時刻相等,進一步整理可得未知函數y(t)的迭代計算公式為

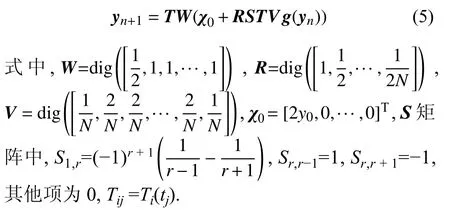
1.2 局部配點反饋迭代法

在式(4)中,迭代公式通過對導數向量積分得到函數值,利用新的函數值更新導數向量并再次進行積分迭代,直到達到目標精度.本節將誤差反饋機制引入迭代過程,結合時域配點法與局部離散化思想,建立一種新的局部配點反饋迭代法.

Picard 迭代公式(4)與下式等價

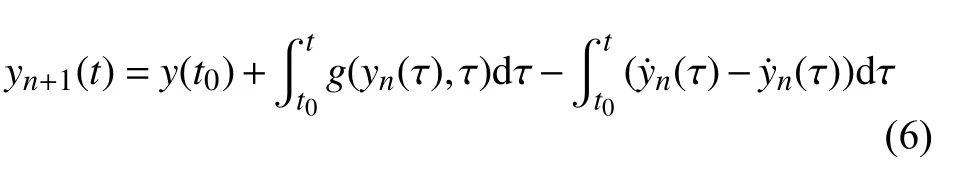
對式(6)進行整理,以導數估計值 y˙n(t) 與利用狀態估計值計算得到的導數值 g(yn(t),t) 之差作為修正項,將式(6)改寫為如下迭代公式

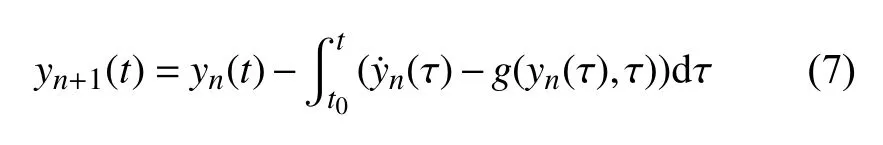
稱式(7)對應的迭代方案為反饋迭代法.

對于[t0,tf]范圍內的任意時刻tm,可以使用下式將其轉化到區間[-1,1]范圍內

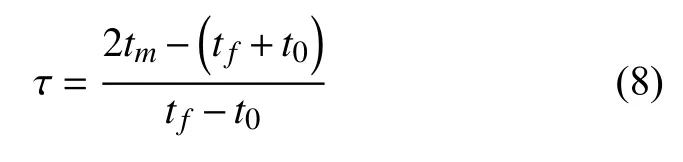
通過式(8) 將求解區間進行轉化后,使用Chebyshev 正交多項式的線性組合作為未知函數y(t)的估計解,即近似認為

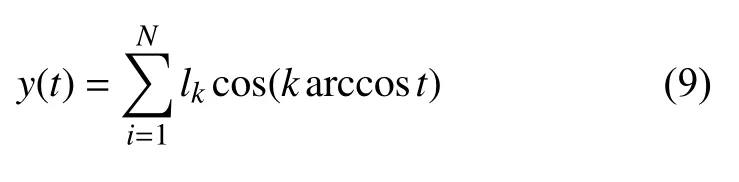
式中,cos(karccost) 為第k 項Chebyshev 多項式在t 時刻的值,lk為第k 項Chebyshev 多項式的系數.

為求解式(9)中N 個未知多項式的系數lk(k=1,2,···,N),對式(9)采用時域配點法[22],即令正交多項式線性組合所構成的函數估計解在N 個給定時刻t1,t2,···,tN與函數真值相等,從而構造由N 個線性方程構成的線性代數方程組

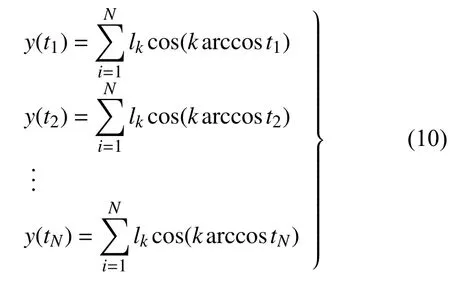
將式(10)記為如下矩陣形式

式中,y 為N 個時刻 t1,t2,···,tN對應的函數真值構成的真值向量,C 為Chebyshev 多項式矩陣,其中第i 行j 列元素Cij=cos(jarccosti),L 為系數向量L=[l1,l2,···,lN]T.

在給定時刻,未知函數的真值與Chebyshev 多項式矩陣C 可以預先求得,因此可以利用下式求解系數向量L

將式(12)得到的系數向量代入式(11),再將式(11)代入式(7),得到配點反饋迭代法的迭代公式

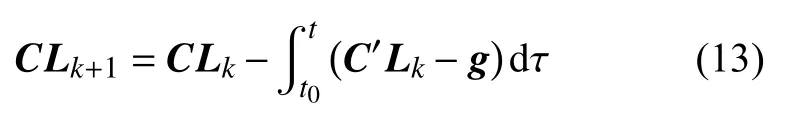
由于Chebyshev 多項式形式已知,對其進行微積分運算可得

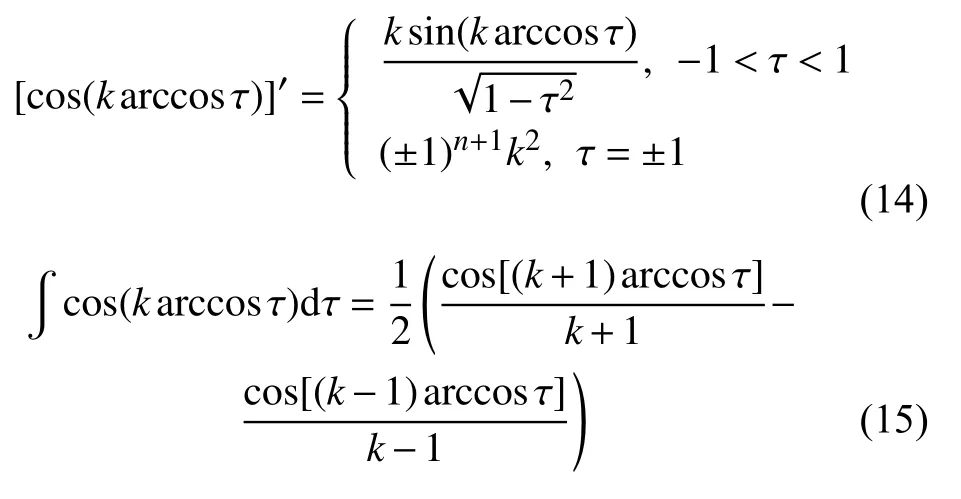
由式(14)及式(15)可以得到Chebyshev 多項式矩陣的微分形式及積分形式.據此可將式(5)推導中涉及的符號運算全部轉化為代數運算,最終得到配點反饋迭代法的迭代計算式

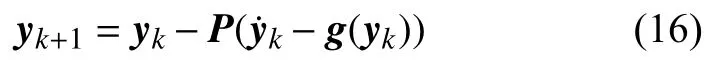
式中,P為積分形式的Chebyshev 多項式矩陣,計算公式為P=

在計算過程中對式(16)反復迭代,直至計算結果精度達到目標要求.此時,得到的系數向量L 中每一項即為使用式(9)作為未知函數估計解時,滿足精度要求的Chebyshev 多項式對應項系數.

Cuthrell 和Biegler[23-24]的相關研究結果指出,將整個函數待解區域作為配點區間,直接得到全局估計解的方法僅適用于求解光滑問題,而對于非光滑或難以直接全局近似估計的問題,應當對全局區域進行離散,并在離散后得到的每個較小子區間內使用正交多項式進行分段估計.考慮到將區間離散化后在每個較小子區間內對未知函數進行估計能夠取得更好的估計效果,在應用配點反饋迭代法時,首先將整個待解區間離散化為多個子區間,從第一個子區間開始對未知函數進行迭代計算,之后將第一個子區間終點函數值作為下一子區間初值,再次使用配點反饋迭代法估計該區間內的未知函數數值解,重復上述過程,直至求得未知函數在全部待解區間內的數值解.這一結合局部離散思想的配點反饋迭代法稱為局部配點反饋迭代法(local collocation feedback iteration method,LCFI),算法計算過程示意圖見圖1.

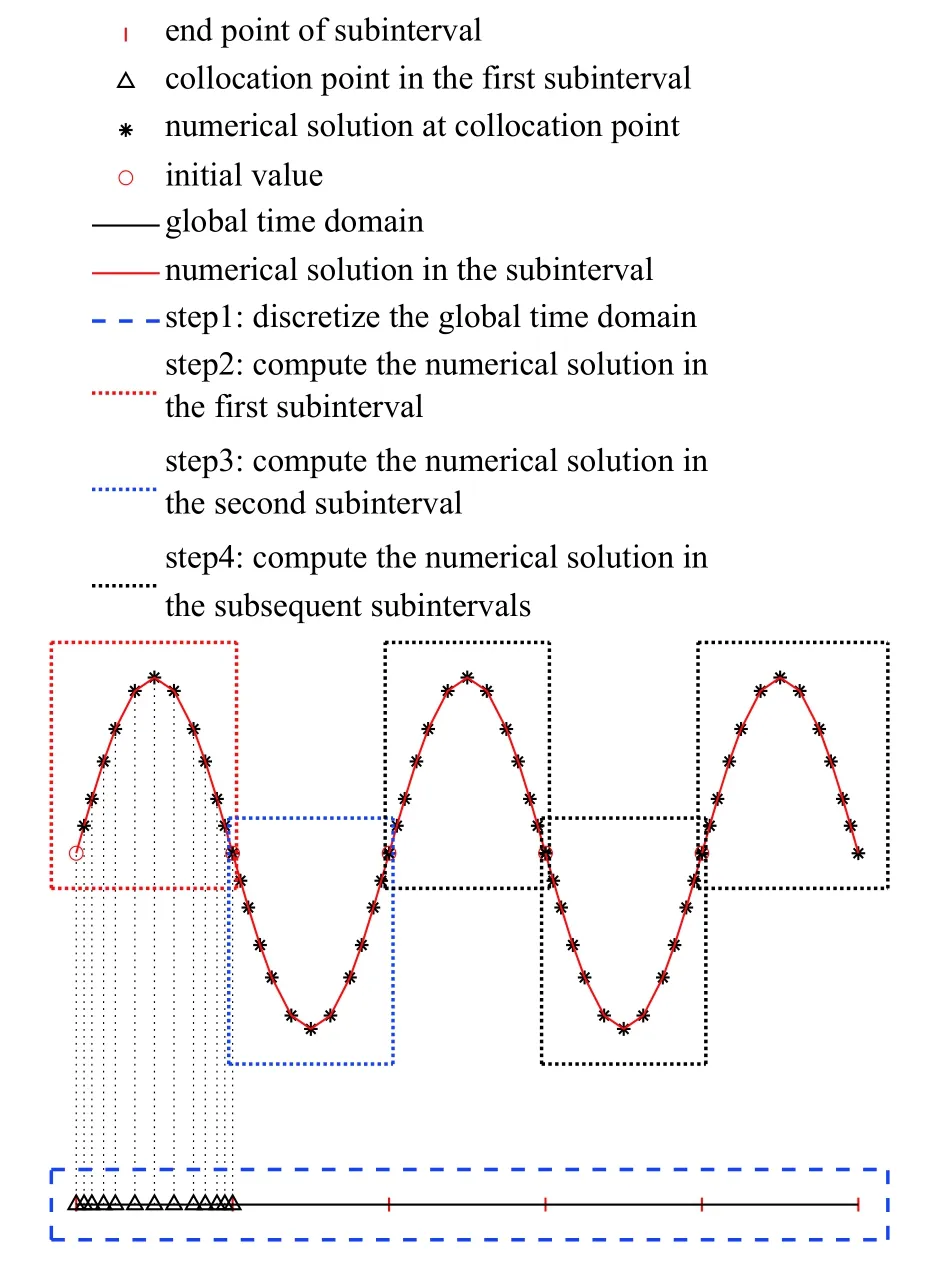
圖1 局部配點反饋迭代法示意圖Fig.1 Illustration of LCFI

本節提出的局部配點反饋迭代法與Picard 迭代法在數學上雖然等價,但式(7)通過結合誤差反饋,將導數殘差作為修正項引入迭代公式,實際計算效率具有明顯優勢.此外,在Bai[17]提出的修正Chebyshev-Picard 迭代算法中,由于其利用多項式正交性計算系數,推導過程十分繁瑣,且迭代公式較為復雜,增加了編程工作量,降低了算法的計算效率.本文通過結合配點法,直接計算正交多項式系數向量,在實際計算中效率更高.汪雪川[25]通過相關數值實驗證明了局部變分迭代法的計算效率高于修正Chebyshev-Picard 迭代算法,在本文下一節的數值仿真中可以看到,本文提出的局部配點反饋迭代法計算效率遠高于局部變分迭代算法.上述事實證明相比于修正Chebyshev-Picard 迭代算法及變分迭代法,本文算法在計算效率上具有顯著的優越性.同時,通過比較本文算法迭代公式與文獻[25]中局部變分迭代算法迭代公式不難發現,本文算法消除了雅可比矩陣,這一特點使得算法能夠更容易的被應用于求解復雜高維問題.

2 擬線性化-局部配點反饋迭代法

局部配點反饋迭代法能夠計算常微分方程初值問題,但不能直接求解Lambert 問題等邊值問題,本節介紹一種將擬線性化法及疊加法與局部配點反饋迭代法相結合的方案,使算法能夠處理兩點邊值約束下的軌道計算問題.

2.1 擬線性化法

擬線性化法是一種將非線性微分方程近似線性化的數學方法[21].

對具有如下形式的二階非線性微分方程邊值問題

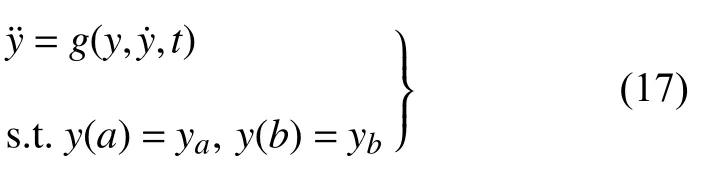
式(17)可以改寫為

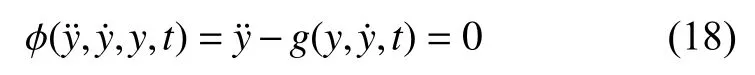
令y0為未知函數y 的初始估計解,yn和yn+1分別表示第n 次和第n+1 次迭代結果,將第n+1 次迭代結果在處展開,略去二階及以上偏導數,可以得到將非線性二階微分方程(17)擬線性化后的迭代計算公式

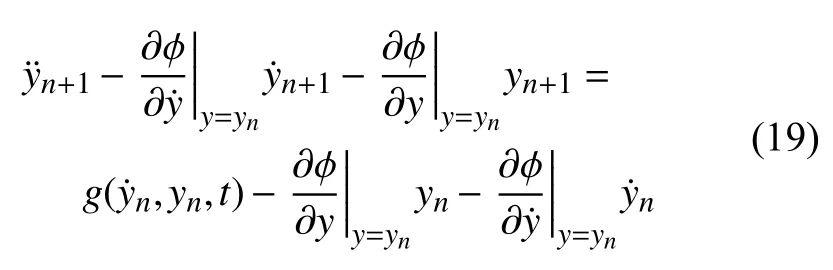
式(19)對應的邊界條件為 yn+1(a)=ya,yn+1(b)=yb.

利用式(19)迭代求解未知函數y,求解過程中,對于第n 次迭代得到的yn,在代入式(19)進行第n+1次迭代時,若將yn視為已知量,則式(19)可視為僅關于yn+1的二階微分方程,求解該方程即可得到yn+1.重復上述迭代過程,當yn+1=yn時,迭代結束,此時yn+1即為微分方程(17)的解.

2.2 疊加法

疊加法能夠將微分方程邊值問題轉化為初值問題[26].對于如下形式的微分方程邊值問題

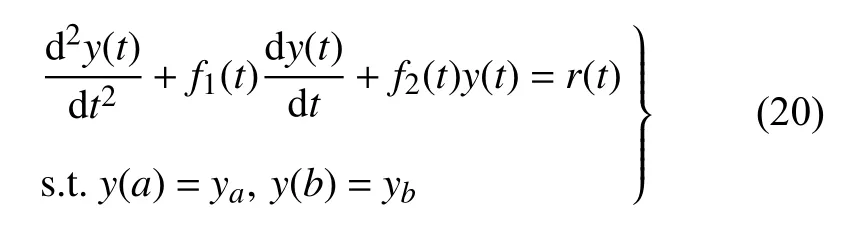
假設解的形式為

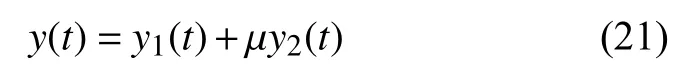
將式(21)代入式(20),可將邊值問題(20)轉化為求解使如下兩個二階常微分方程成立的未知函數y1與y2

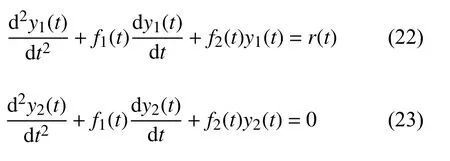
滿足邊界條件的y1與y2可由如下兩組微分方程初值問題分別求得

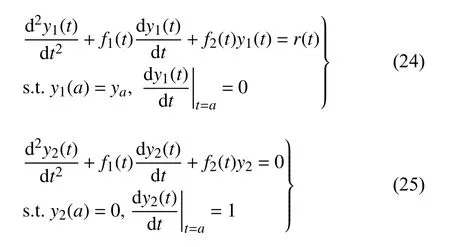
滿足邊界條件的μ 由下式計算得到

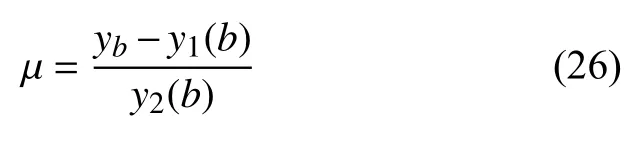
在計算時,首先求解式(24)和式(25)兩個微分方程初值問題得到y1(t)與y2(t),之后將b 點的兩個函數值y1(b)與y2(b)代入式(26)計算μ,最后,將μ及y1(x)與y2(x)代入式(21),得到未知函數y(x)的解.

對于Lambert 問題等兩點邊值條件約束下的軌道動力學問題,首先利用擬線性化法將其轉化為二階線性微分方程邊值問題,再利用疊加法將二階線性微分方程邊值問題轉化為一組初值問題,使用局部配點反饋迭代法對初值問題分別求解,再依據式(21)即可得到兩點邊值問題的解.

3 數值仿真結果

3.1 軌道遞推

軌道遞推問題的動力學方程為

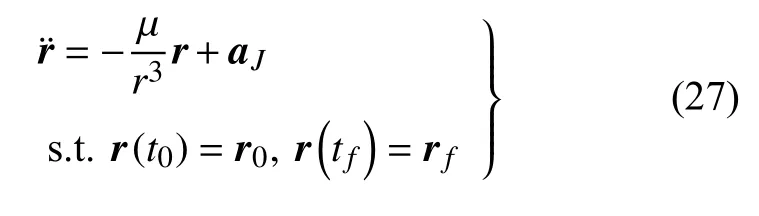
式中,r=[x,y,z]T,表示航天器的位置矢量,μ=3 986 004.418 × 108m3/s2,表示地球引力常數,r=‖r‖,表示地心與航天器質心間的距離,t0為軌道遞推初始時刻.aJ為攝動項,本算例中考慮J2項攝動.

軌道遞推為初值問題,在給定初值條件的情況下,可以使用局部配點反饋迭代法直接求解.本文通過連續100 次仿真實驗比較算法性能.為了與同類方法的計算性能進行對比,本算例使用文獻[21]中軌道遞推問題初始位置,相關計算參數見表1,100 次仿真平均單次計算時間比較結果見表2.

表1 遞推軌道計算參數Table 1 Calculation parameters of LCFI in orbit propagation

表2 軌道遞推計算效率對比Table 2 Comparation of efficiency on orbit propagation

由表2 可見,在相同配點條件及計算精度下,針對軌道遞推問題,局部配點反饋迭代算法(LCFI)的計算速度為局部變分迭代法(LVIM)的1.5 倍以上(1.78 倍),在相同精度要求下,LCFI 算法的計算效率更高.進一步的仿真結果表明,當配點個數上升到32 個時,在表1 計算精度條件下,LCFI 算法計算步長可以達到12 000 s,而基于有限差分原理的ode113 算法與ode45 算法計算步長均小于1200 s(最大步長分別為889.9 s 與1 147.3 s),本文算法在上述問題中能將計算步長提高到有限差分類算法的10 倍以上.

LCFI 與LVIM 計算結果及誤差見圖2～ 圖4,對于7 日內的軌道遞推結果,兩種算法所得目標軌道最大絕對誤差小于0.4 m,最大相對誤差小于4.9 ×10-8,這樣的計算精度在工程實際中是可以接受的.同時,從圖3 絕對誤差變化曲線與圖4 相對誤差變化曲線可以看出,算法在迭代過程中能夠對誤差進行周期性自動修正,從而降低誤差發散速度.

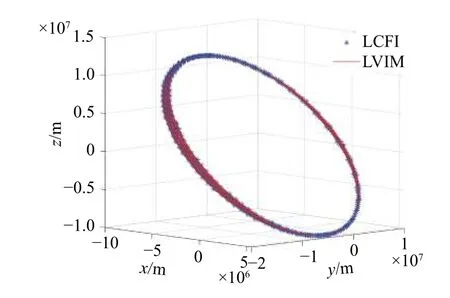
圖2 LCFI 與LVIM 所得遞推軌道對比Fig.2 Comparison between orbits propagated via LCFI and LVIM

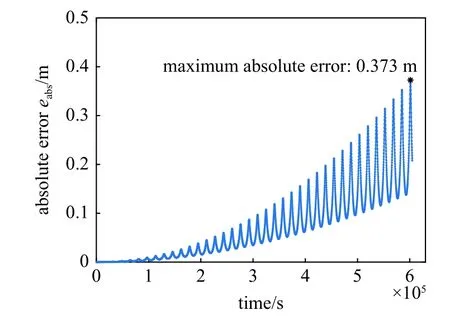
圖3 LCFI 與LVIM 所得遞推軌道絕對誤差Fig.3 Absolute error of the orbits propagated via LCFI and LVIM

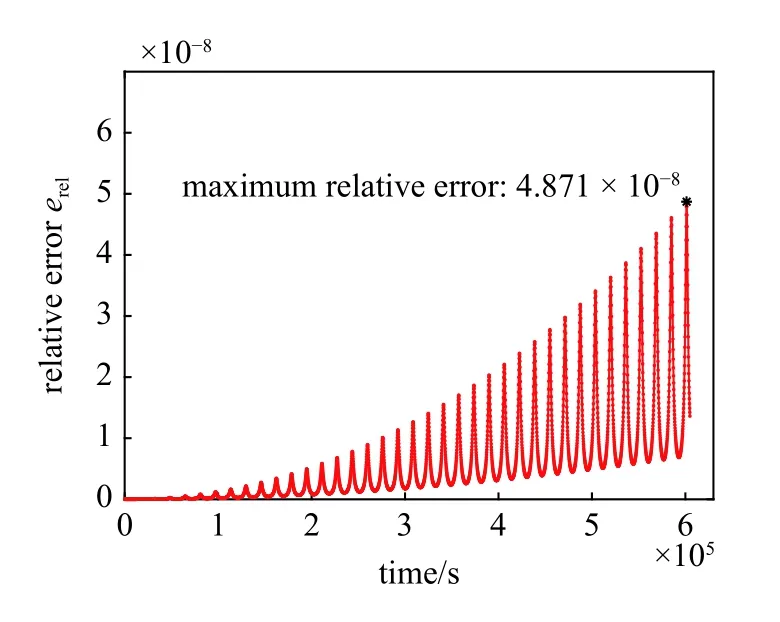
圖4 LCFI 與LVIM 所得遞推軌道相對誤差Fig.4 Relative error of the orbits propagated via LCFI and LVIM

3.2 攝動Lambert 軌道

Lambert 軌道轉移問題是經典的軌道力學問題,也是航天器軌道動力學快速計算方法研究中常用的求解對象[21,25].本節對攝動Lambert 轉移軌道及轉移初速度進行求解,并與擬線性化-局部變分迭代算法求解結果及計算效率進行對比,驗證LCFI 算法的精確性及快速性.

攝動Lambert 問題的動力學方程與式(27)所示二體軌道動力學系統的遞推問題相同,將式(27)右側記為g(r),擬線性化處理后的Lambert 問題動力學方程及其邊界條件表達式為

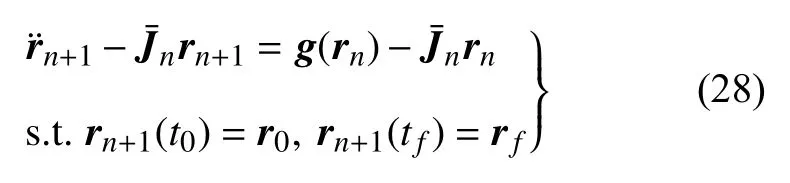
依據疊加法,將 rn+1寫為如下形式

其中 r1與 r2利用如下兩個微分方程初值問題求得

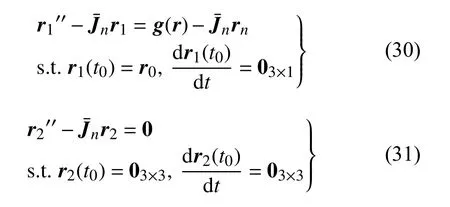
式(29)中μ 由下式求得

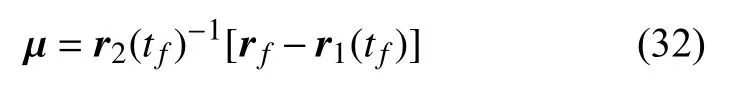
為與同類方法的計算性能進行對比,本算例同樣使用文獻[21]中Lambert 轉移問題對應的始末位置條件,坐標系采用地球固連坐標系,經過連續100 次仿真,單次平均用時見表3,初始條件及相關計算參數見表4,計算所得軌道結果及不同算法所得軌道計算誤差見圖5～ 圖7.

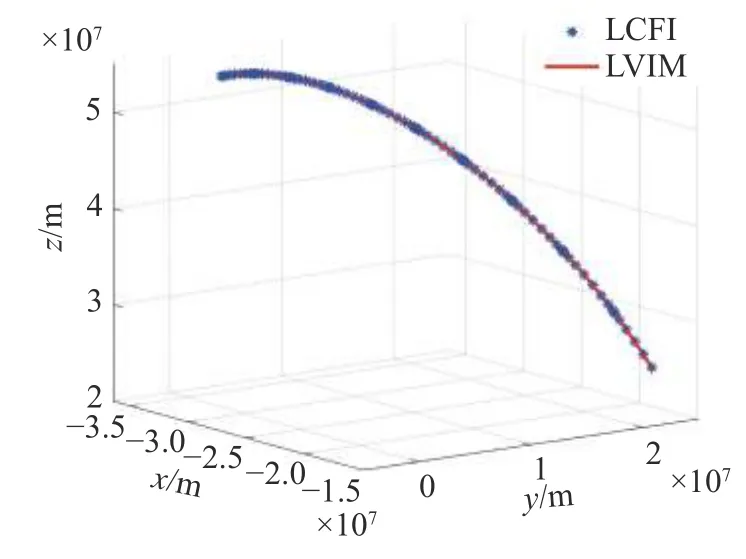
圖5 LCFI 與LVIM 所得Lambert 轉移軌道結果對比Fig.5 Comparison between Lambert orbits obtained via LCFI and LVIM

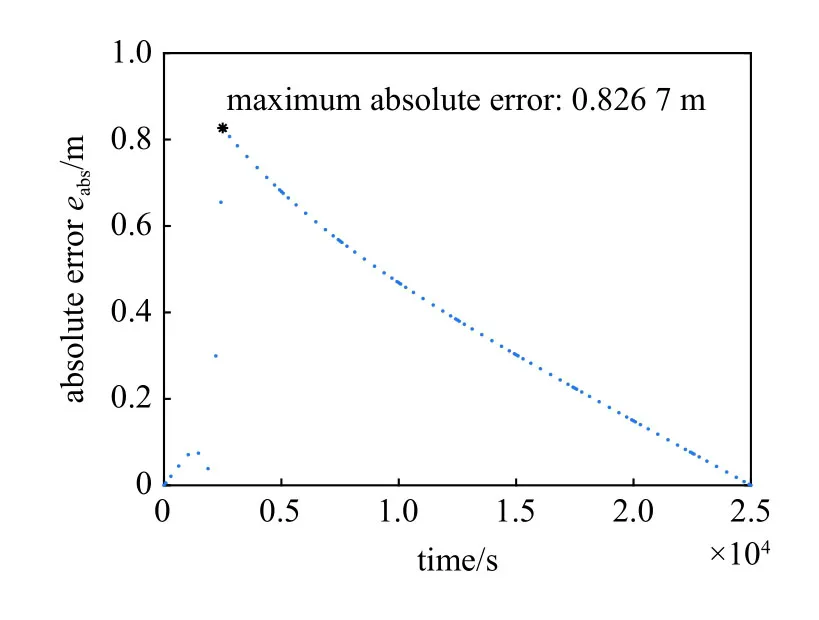
圖6 LCFI 與LVIM 所得Lambert 轉移軌道絕對誤差Fig.6 Absolute error of Lambert orbits obtained via LCFI and LVIM

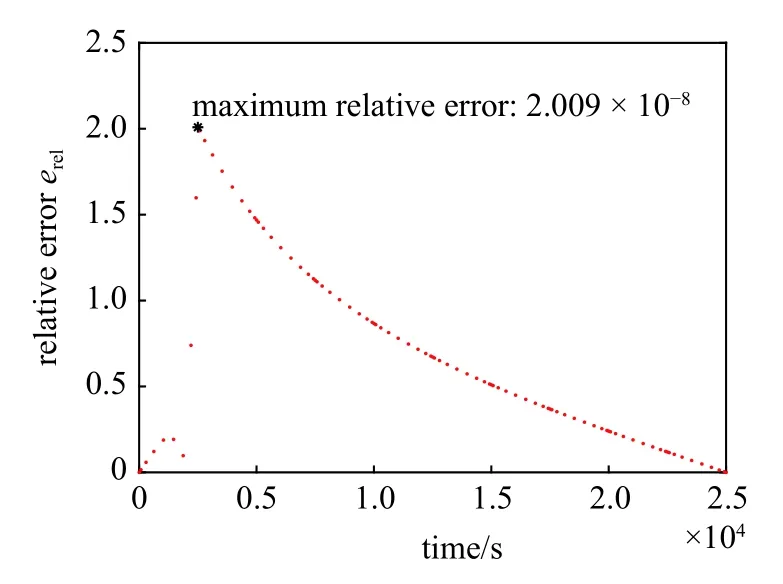
圖7 LCFI 與LVIM 所得Lambert 轉移軌道相對誤差Fig.7 Relative error of Lambert orbits obtained via LCFI and LVIM

表3 攝動Lambert 問題計算效率對比Table 3 Comparation of efficiency on Lambert problem

表4 攝動Lambert 轉移軌道計算參數Table 4 Calculation parameters of LCFI in perturbed Lambert problem

表3 表明,在相同計算參數及計算精度條件下,針對攝動Lambert 軌道轉移問題,局部配點反饋迭代法(LCFI)計算速度為文獻[21]中擬線性化-局部變分迭代算法(QL-LVIM) 的2 倍以上(2.68 倍).

在計算結果精度方面,LCFI 算法計算得到的軌道轉移初速度為[-1 687.309 900 000,-0.024 275 234,2 922.608 000 000] m/s,LVIM 算法計算得到的軌道轉移初速度為[-1 687.309 900 000,-0.024 305 875,2 922.607 900 000] m/s,兩種算法求得的轉移初速度絕對誤差二范數小于1.05 × 10-4m/s,相對誤差二范數小于3.10 × 10-8,速度計算誤差遠小于實際測量與控制精度,這樣的計算誤差在實際應用中是可以忽略的.在計算誤差變化趨勢方面,由圖6 及圖7 可見,針對本算例中的攝動Lambert 軌道,兩種算法對位置計算結果的最大絕對誤差不超過0.83 m,最大相對誤差不超過2.1×10-8,且整個計算過程中誤差經過初期增長后受到抑制,在后續計算過程中呈下降趨勢.

3.3 圓型限制性三體模型約束下轉移軌道

當兩個主要天體圍繞其系統質心做圓周運動,同時存在一個質量可忽略的第三天體在兩個主要天體運動的公共平面內運動,這樣的問題就構成了平面圓形限制性三體問題[27].月球探測航天器在地-月轉移過程中,運動范圍始終位于地球影響球內,而地-月系本身圍繞系統質心旋轉,因此在初步設計地-月間循環軌道時,可以將航天器的運動簡化為地-月-航天器圓形限制性三體問題模型(circular restricted three body problem,CR3BP),該模型也是描述星際探測航天器軌道轉移問題的經典非線性模型[28-33],本節通過解算該模型驗證LCFI 算法的有效性.

對于地球、月球、航天器構成的三體系統,令地-月系質心為坐標系原點,x 軸正方向由地球質心指向月球質心,地-月系軌道平面為(x,y)平面,z 軸與地月系統軌道面垂直,建立空間右手直角坐標系.設地球質量為m1,月球質量為m2,地球到坐標系原點距離為l1,月球到坐標系原點距離為l2,將地月間距離及地月系質量均無量綱化為1,即令月球的無量綱質量為μm,地球的無量綱質量為1-μm,地球到原點的距離為μ,月球到原點的距離為1-μ,航天器的無量綱形式運動方程為[33]

式(33)表征的圓形限制性三體問題動力學模型中,在其L1,L2以及L3拉格朗日點附近存在對應于系統某一周期解的Halo 軌道.由于Halo 軌道附近存在著類似管道的不變流形,航天器在流向Halo 軌道的穩定流形中運動時幾乎不需要消耗能量,能夠顯著節約燃料[34],因此Halo 軌道及其不變流形常常被用于設計低成本登月軌道[9,35-38].

在由近地軌道或繞月軌道向不變流形轉移的過程中,需要對航天器運動狀態進行多次調整,這一過程中的轉移軌道需要精確計算[21].本節算例通過計算探月航天器從185 km 高度地球停泊軌道向流向L1點的穩定流形機動時的轉移軌道,驗證算法在圓形限制性三體問題動力學模型中軌道計算的的高效性.為了與同類方法的計算性能進行對比,本算例使用文獻[21]中該算例計算參數,具體計算參數見表5,其中轉移時間以地月系統運動周期作為系統的無量綱時間2π,相關轉移時間的計算以此為基準,連續100 次計算時間比較結果見表6.計算所得軌道結果及不同算法所得軌道計算誤差見圖8～ 圖10.

表5 圓型限制性三體模型約束下轉移軌道計算參數Table 5 Calculation parameters of LCFI in transfer orbit calculation problem with the constraint of circular restricted three-body model

表6 圓形限制性三體模型約束下轉移軌道計算效率對比Table 6 Comparation of efficiency on transfer orbit calculation problem with the constraint of three-body model

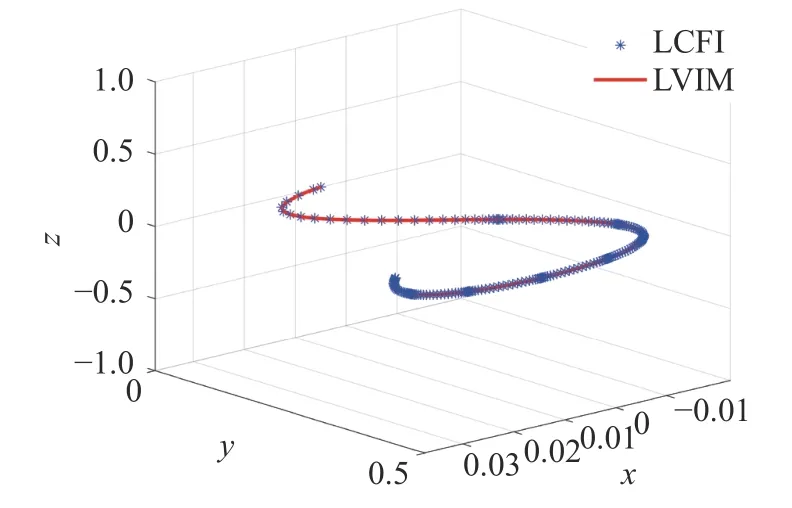
圖8 LCFI 與LVIM 軌道計算結果對比Fig.8 Comparison between orbits obtained via LCFI and LVIM

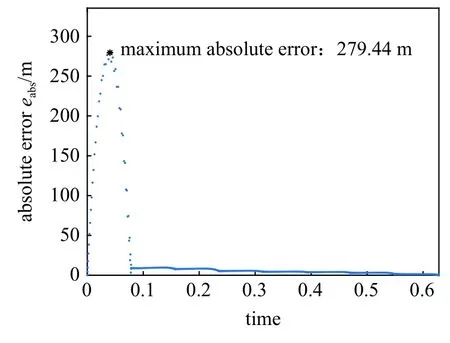
圖9 LCFI 與LVIM 對平面圓形限制性三體模型約束下轉移軌道計算絕對誤差Fig.9 Absolute error of transfer orbits under the constraint of circular restricted three body model obtained via LCFI and LVIM

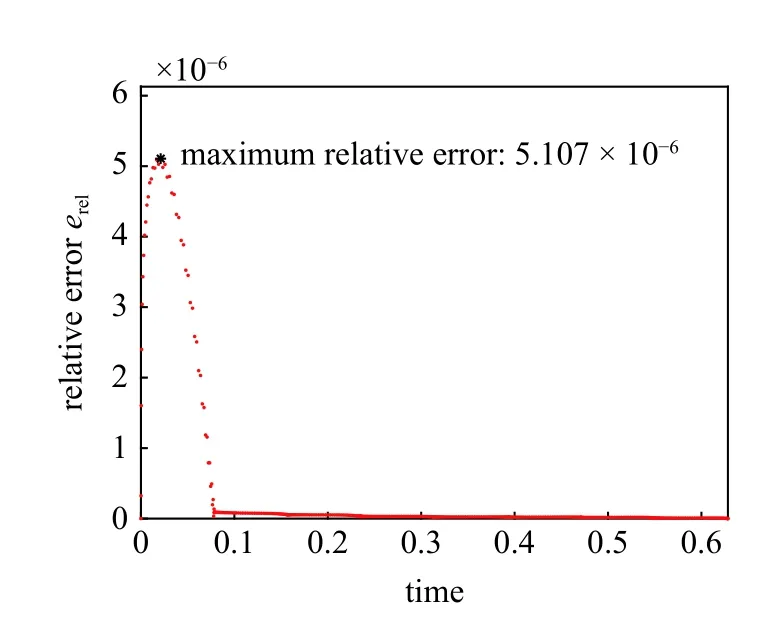
圖10 LCFI 與LVIM 對平面圓形限制性三體模型約束下轉移軌道計算相對誤差Fig.10 Relative error of transfer orbits under the constraint of circular restricted three body model obtained via LCFI and LVIM

由表6 可見,在相同計算參數條件下,針對平面圓形限制性三體模型約束下的軌道轉移問題,LCFI 的計算速度為LVIM 的6 倍以上(6.92 倍),即在相同精度要求下,LCFI 算法的計算效率更高.從圖9 及圖10 誤差變化趨勢來看,誤差在計算初期增長后迅速受到抑制,最大絕對誤差小于279.5 m,最大相對誤差小于5.2 × 10-6.

4 變參數計算方案及仿真實例

本文提出的局部配點反饋迭代法相比于傳統數值積分方法具有大步長計算特性,為發揮算法大步長收斂優勢,在滿足工程計算精度要求的基礎上盡可能減少計算量,本文借鑒ph 網格細化法(ph mesh refinement method)[39-40]計算思想及針對該方法的相關改進策略,將變參數計算方案引入本文算法,從而使得局部配點反饋迭代法能夠自適應選擇具有更高計算效率的參數組合.

4.1 變參數計算方案

參數變化算法流程圖見圖11,具體的自適應參數調節過程分為兩部分.

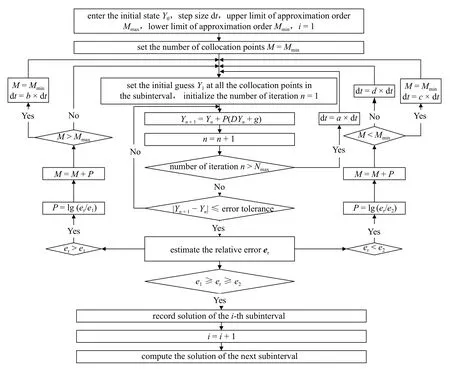
圖11 變參數局部變分迭代算法流程圖Fig.11 Flow chart of adaptive local collocation feedback iteration method

(1)在一個子區間內,迭代計算精度大于迭代終止誤差限,但迭代次數超過預定的迭代計算終止次數Nmax時,將當前區間的計算步長減小為原來的a 倍(a＜1),并對當前計算區間內各配點時刻對應的函數值重新進行計算.

(2)在一個子區間內,迭代計算精度達到迭代終止誤差限,且迭代次數小于預設定的迭代計算終止次數Nmax時,首先對子區間內M 個節點狀態進行插值,利用插值函數計算子區間配置M+1 個節點時各節點狀態估計值.其次對子區間內M 個節點的導數估計結果進行插值,并利用插值函數計算子區間配置M+1 個節點時各節點的導數估計值,對導數估計值積分后得到子區間內M+1 個節點函數狀態估計值.根據相關研究結果,兩次估計結果差的模值與當前對M 個節點的估計結果的誤差基本相等[39],因此可以使用該方法對當前計算結果的誤差進行估計,上述相對誤差計算過程的具體計算公式如下

當計算結果的相對誤差向量er中值最大的元素高于規定的誤差上限e1時,此時計算結果誤差過大,需要增加計算精度以滿足計算精度要求.當計算結果的相對誤差向量er中最大元素低于規定的誤差下限e2時,需要適當降低計算精度以提高計算速度.依據ph 網格細化法,需用節點個數計算公式為

式中,er＞e1時P=lg(er/e1),er＜e2時P=lg(er/e2),M2為計算所得的需用節點個數,M1為當前的節點個數.

當計算結果的相對誤差er大于規定的誤差上限e1且需用節點個數大于節點數上限Mmax時,令當前計算區間的步長降為當前步長的b 倍(b＜1),節點數等于最小節點個數,并重新計算當前區間內各個節點函數值.當計算結果的相對誤差er大于規定的誤差上限e1且需用節點個數小于節點數下限Mmax時,令節點數等于需用節點個數,并重新計算當前區間結果.當計算結果的相對誤差er低于規定的誤差下限e2且需用節點個數小于節點數下限Mmin時,令當前計算區間的步長增加到當前步長的c 倍(c＞1),節點數等于最小節點個數,并重新計算當前區間結果.當計算結果的相對誤差er低于規定的誤差下限e2且需用節點個數大于節點數下限Mmin時,令節點數等于需用節點個數,并令當前計算區間的步長增加到當前步長的d 倍(d＞1),重新計算當前區間結果.當計算結果的相對誤差er高于規定的誤差下限e2且低于規定的誤差上限e1時,保留當前區間計算結果與計算參數設置情況,并進行下一區間的計算.

4.2 仿真實例

近年來,微小衛星在航天工程領域受到了廣泛關注.缺乏推進系統的微小衛星在軌運行狀況發射前需要依賴軌道動力學模型經過數值計算得到.目前,微小衛星大多運行于近地軌道,在該軌道上航天器受到的最主要干擾力為地球非球形攝動,其大小比其他攝動力高出3 個量級以上[41],本文基于40 階EGM2008 球諧重力場模型,在相同初始計算參數及迭代計算精度下,計算兩組不同初始條件下衛星軌道經過12 960 400 s (15 天)后的目標位置.初始計算參數見表7 及表8,變參數LCFI 相關計算參數見表9,計算用時見表10,不同算法計算結果見圖12 及圖13,計算過程中參數變化情況見圖14～ 圖17.

表7 圓軌道遞推初始計算參數Table 7 Calculation parameters of orbit propagation

表8 橢圓軌道遞推初始計算參數Table 8 Calculation parameters of orbit propagation

表9 變參數LCFI 遞推軌道計算參數Table 9 Calculation parameters of adaptive LCFI in orbit propagation

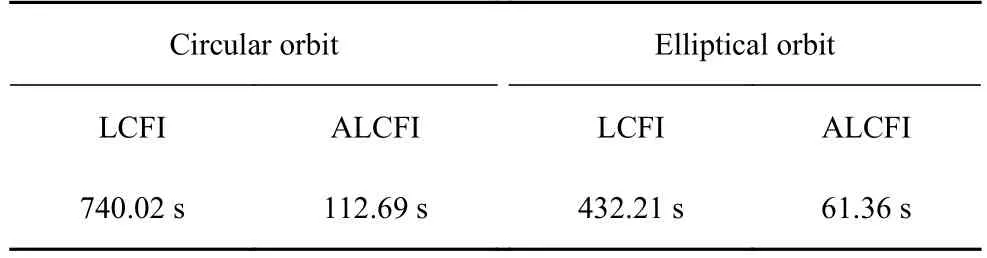
表10 不同算法計算時間Table 10 Time cost of different numerical method

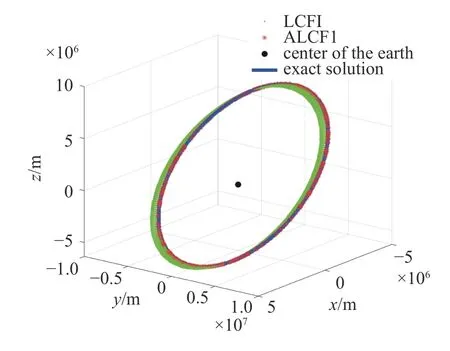
圖12 變參數LCFI 及定參數LCFI 圓軌道遞推計算結果Fig.12 Circular orbit obtained via Adaptive LCFI and LCFI

圖13 變參數LCFI 及定參數LCFI 橢圓軌道遞推計算結果Fig.13 Elliptical orbit obtained via adaptive LCFI and LCFI

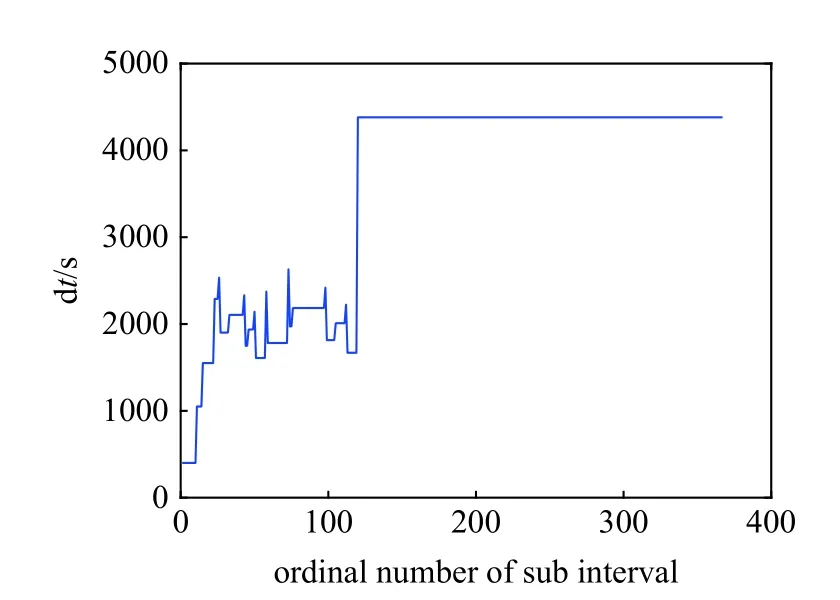
圖14 變參數LCFI 圓軌道遞推計算步長變化Fig.14 Step size of ALCFI in the propagation of a circular orbit

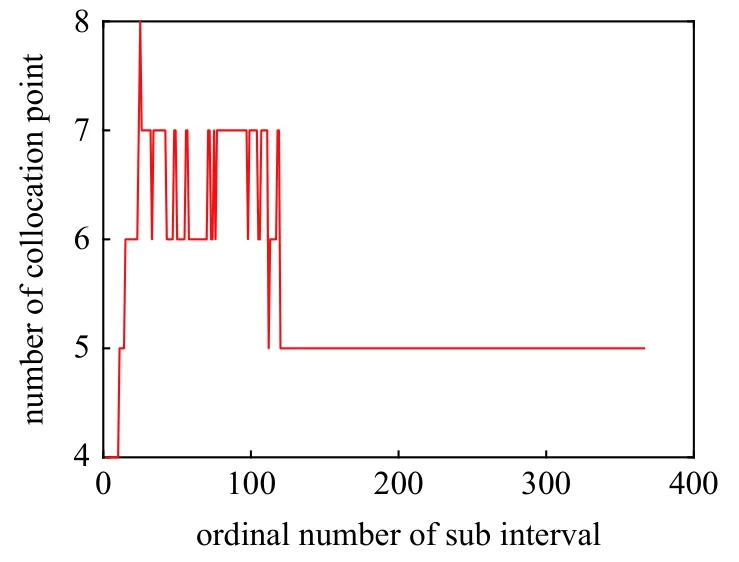
圖15 變參數LCFI 圓軌道遞推計算配點數變化Fig.15 Variation of the collocation point number in the propagation of a circular orbit

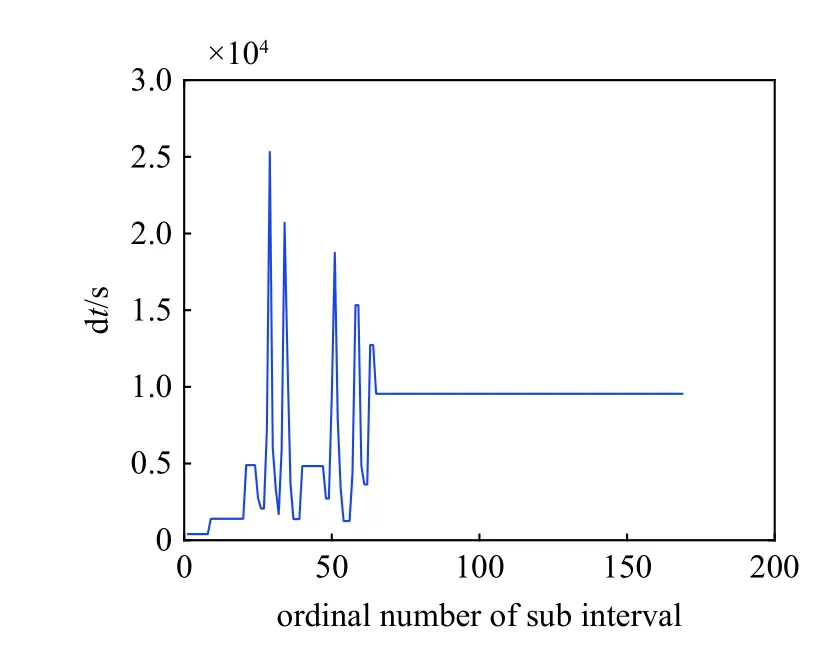
圖16 橢圓軌道遞推計算步長變化Fig.16 Step size of ALCFI in the propagation of an elliptical orbit

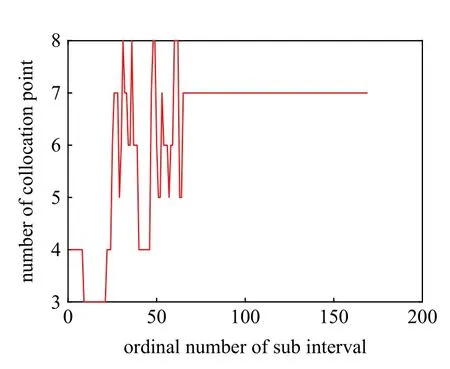
圖17 橢圓軌道遞推計算配點數變化Fig.17 Variation of the collocation point number in the propagation of an elliptical orbit

根據圖14～圖17 可見,針對考慮40 階EGM2008地球球諧重力場模型的軌道遞推問題,在相同初始計算參數及迭代計算精度條件下,變參數LCFI 算法能夠自適應選擇更優的計算步長及基函數階次,從而降低計算量.

根據表10 可見,變參數LCFI 計算速度是定參數LCFI 的6 倍以上(6.57 倍與7.04 倍),定參數LCFI 由于初始計算參數設置的合理性不足,限制了算法自身大步長高速計算特性的發揮,該問題通過本節變參數計算方案得到了有效解決.

從圖12 及圖13 可以看出,由于變參數計算方案中引入了誤差評估機制,在航天器高精度軌道預測問題中,相同迭代計算精度下,變參數局部配點反饋迭代法的(ALCFI)計算結果基本落在精確參考軌道附近,而采用定參數局部配點反饋迭代法的(LCFI)的軌道計算結果則產生了更大程度的偏離(圖12 及圖15 中精確參考軌道均使用Matlab 軟件中ode45 程序計算得到,ode45 設置精確參考軌道計算相對誤差2.3 × 10-14,絕對誤差1 × 10-14m),表明變參數計算方案引入的誤差評估與調節機制能夠進一步提高局部配點反饋迭代法計算結果精度.

5 結論

針對在軌航天器軌道動力學系統快速解算需求,本文基于積分補償迭代思想,提出了一種適用于軌道動力學快速計算的高性能數值積分方法,有效克服了傳統數值差分類方法的缺陷.主要工作與結論總結如下.

(1) 結合Picard 迭代法、誤差反饋思想和時域配點法,提出了一種能夠高效求解微分方程初值問題的局部配點反饋迭代法.

(2) 將局部配點反饋迭代法和擬線性化法及疊加法相結合,求解了軌道轉移兩點邊值問題.

(3) 通過解算遞推軌道、攝動Lambert 軌道轉移問題以及圓型限制性三體模型約束下的轉移軌道問題驗證了本文算法的有效性.計算結果顯示在相同迭代精度及計算參數設置條件下,本文算法在上述軌道問題中計算效率比局部變分迭代算法提高50%以上.

(4) 將變參數計算方案引入局部配點反饋迭代法,使算法能夠自適應調節計算參數.相關計算結果表明,本文引入的變參數計算方案能夠在保證計算精度條件下發揮算法大步長快速收斂優勢,并進一步提高算法計算精度.

局部配點反饋迭代法對軌道動力學初值問題及兩點邊值問題的計算效率相較于現有方法具有明顯優勢,在計算能力較弱的星載計算機中[42],該優勢對計算時間的節約程度將更為顯著,這對執行失效衛星抓捕等空間快速機動任務具有重要意義.在后續工作中,將探究局部配點反饋迭代法的并行算法設計等改進方案,以進一步提高算法性能.