基于特定有限交互規則的無人機集群協同控制

朱柏濤，鄧亦敏，段海濱

(北京航空航天大學自動化科學與電氣工程學院，北京 100083)

0 引言

近年來，無人機在電力巡檢、應急救災、城市規劃、數字城市等方面均有廣泛的應用。隨著無人機應用逐漸深入，無人機技術也得到了飛速地發展[1-2]。由于單架無人機常具有航時短、處理復雜任務差等特點，多無人機在復雜任務完成中具有更加優秀的性能[3-4]，因此無人機集群也是一項熱點研究[5-6]，對其的研究具有重要意義。

無人機集群的協同控制主要包括集中式、分布式兩種[7],集中式控制需要集群中存在長機或中心控制節點，若其失效則會造成集群整體癱瘓。分布式控制可以避免此問題，不存在中心控制節點。分布式控制中每個個體常常需要通過對于周圍個體的感知來最終決定自身行為，因此基本不存在一個個體失效造成集群整體癱瘓的問題。常見的集群分布式框架包括經典的Vicsek模型[8]和Couzin三區域模型[9]。在此基礎上，研究者設計了多種機制并應用于集群系統的分布式系統控制中[10-12]。文中在現有模型基礎上，去除Couzin模型中的吸引區，通過設計合理的速度以及位置協調力，即交互機制，實現整個集群的協調運動；同時，根據不同任務階段，對速度協調力進行具體設計，以實現不同任務階段的特定需求。

經典的Vicsek和Couzin模型在可交互對象選擇上，認定間距小于某設定距離的個體間即可存在交互。此方法對于集群系統的通信能力要求較高，不易于實際驗證，因此考慮有限交互下的集群協同控制十分重要。為此，研究者仿照自然界中大規模鳥群的飛行現象，設計了基于拓撲度量的鄰居選擇方式[13-14]和基于Delaunay三角剖分的鄰居選擇機制[15]。前者規定一個個體僅能與其周圍最近的特定數量的個體進行交互，其在后續研究中被認為不符合實際情況；而后者基于個體視覺的考慮，采用Delaunay三角剖分來選取其一周的鄰居，而忽視較遠端的鄰居，需要注意的是其建立往往需要全局信息，與分布式控制的要求相違背。因此，文中提出了一種基于有限視場限制下隨機視線遮擋關系的鄰居選擇機制，即有效交互方式，在限制通信的情況下，盡可能多的保證可交互對象的多樣性。

分別考慮集群初始混亂情況下的安全性和集群運動中的協同性，將集群飛行任務分為初始階段和集群運動階段。在所設計的有限交互和交互機制作用下，初始混亂階段無人機集群能快速實現位置無人機間安全距離的保持，在集群運動階段能實現對隨機領導者的緊密跟隨。

1 問題描述

1.1 場景描述

假設一組初始狀態下位置關系混亂(存在位置較近，具有碰撞風險)的無人機，現期望所有無人機集群在初始階段首先通過局部交互實現個體間位置上的安全性，然后隨機地向集群中引入少數領導者，集群進入運動階段，其余無人機在有限交互的情況下實現對于領導者的跟隨，最終實現整個無人機群體整體的協同運動控制。圖1為任務場景執行流程。

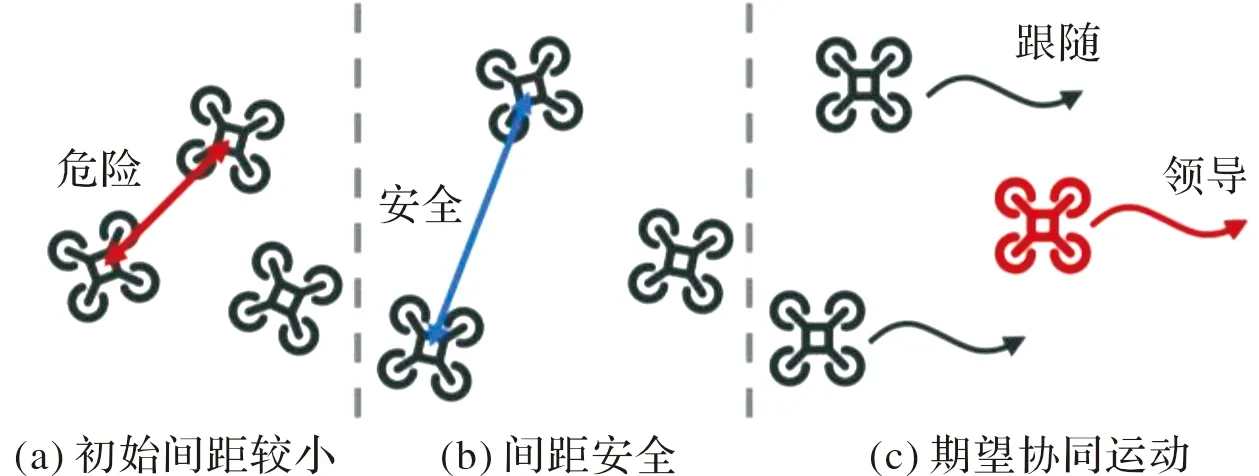
圖1 任務場景執行流程

1.2 對象描述

假設由n個四旋翼無人機組成的集群系統，可在三維無障礙空間中飛行，每架無人機具有良好的位置、速度控制能力，可實現空中的懸停。其中每架無人機的運動模型可表示為雙積分模型[16]：

(1)

式中：i∈[1,n]；pi,vi分別為無人機i的位置及速度向量；ui為無人機i的加速度控制輸入，該控制量來自個體與其鄰居的交互，具體可表示為：

(2)

式中：Ni表示無人機i的可交互鄰居集合；fji表示無人機i與無人機j之間的作用力。

進一步考慮無人機飛行性能限制，給出無人機速度及加速度限制：

(3)

同時，為了實現集群運動的協同控制，假設無人機能感知其可交互對象的位置以及速度信息并進行通信。

2 有限交互機制設計

有限交互機制的設計包括有限交互方式的設計和交互機制的設計。有限交互方式設計是指無人機如何在局部范圍內確定可交互對象，即鄰居選擇；交互機制設計是指在確定可交互鄰居后，根據鄰居信息進行自身期望狀態的決策。現就以上兩個方面分別進行闡述。

2.1 有限交互方式設計

有效交互方式設計等同于可交互鄰居選擇方式設計，參考典型鳥群行為[17-18]設計了一種基于有限視場限制下隨機視線遮擋關系的鄰居選擇機制。為仿照生物視覺特性設計了有限視場(visual field，VF)限制，此方式可有效減少可交互對象的數目。同時，為避免視線方向單一造成的鄰居情況恒定，最終導致集群運動發散的情況，采用了隨機視線機制，即無人機視線方向與機頭朝向之間夾角大小隨機。此方法可以有效提高鄰居的多樣性，降低了鄰居恒定的可能性。

可交互鄰居選擇機制如圖2所示，圖中灰色個體明顯處于中心個體的視覺感知區外，則其不為中心個體鄰居。而藍色及橘色個體雖均處于中心無人機的視覺感知范圍內，但考慮視線遮擋關系，橘色個體與中心個體間的視線交互被其間的藍色個體遮擋，因此橘色個體也不為中心個體的鄰居。同時，中心個體視線(line of sight，LoS)與其速度(機頭朝向)間的夾角大小隨機。

圖2所設計的鄰居選擇機制可描述為：

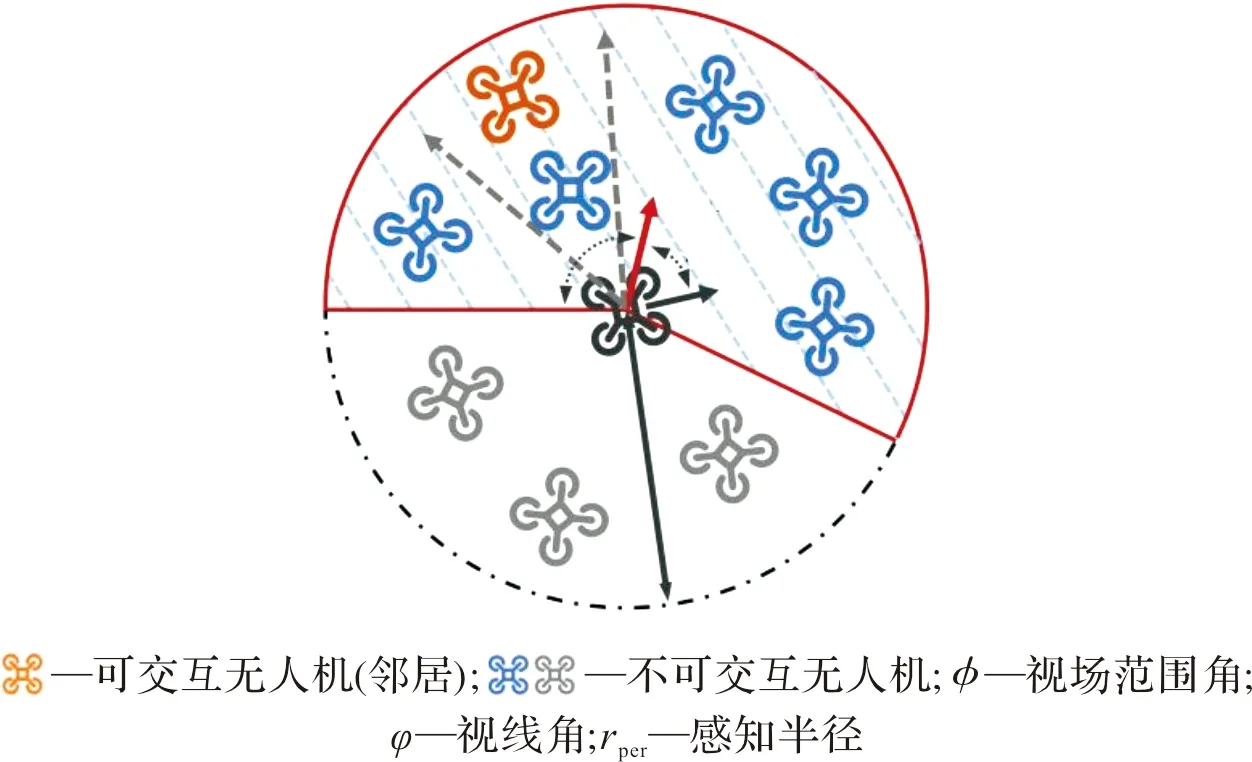
圖2 可交互鄰居選擇機制

φi～U(-ALoS,max,ALoS,max)

(4)

Ni={j|Vi(φi)∩Ωj≠?|}

(5)

式中：φi為無人機i的視線角；U(·)表示均勻分布的概率密度函數；ALoS,max表示視線角最大范圍；Vi(φi)為無人機i在視線角限制下的視場區域；Ωj表示無人機j的空間區域，此區域由無人機個體體積決定，可利用無人機空間半徑rUAV表示。

2.2 交互機制設計

在確定了可交互鄰居后，中心無人機需根據其鄰居的相關信息(如位置、速度)，進行自身期望狀態的生成。根據任務場景描述，無人機集群首先需要保證飛行過程中的安全性，此安全性主要由近距距離表征，即無人機間距在飛行過程需保證在最短距離之外，實現集群的位置協同。同時，為實現集群整體的協同運動，需要為無人機速度協同保留足夠的空間，即保證無人機在充分的時間、空間內能夠完成群體協同運動的目的。綜上分析，將傳統交互機制中排斥區、對齊區、吸引區的三區域模型改為僅有排斥區與對齊區，此方法首先在近距距離保證了無人機個體間的位置安全性；其次由于取消了吸引區，使得對齊區的空間增大，更有助于集群的速度協同。

飛行安全是需要解決的重要問題，為此設計排斥力(即位置協同力)如式(6)。考慮到距離越近碰撞風險越大，因此當機間間距越近時其排斥力越大。

(6)

式中：fp,ji為無人機j對無人機i的位置協同力；rij=pj-pi；rrep表示排斥區半徑；Krep為斥力系數。

對于速度協同量的設計需要考慮任務階段，由于在初始情況下無人機位置分布較為混亂、個體間距較小，此階段需主要解決個體間距問題。對于速度的協同需配合位置協同進行，當中心個體與鄰居間距合理，中心個體做減速處理以保證當前的安全距離。具體設計如下：

fv,i=-Kv,inivi
s.t.si=Initial,i∈[1,N]

(7)

式中：fv,i為無人機i速度協同力；rper為無人機感知半徑；si表示無人機i當前任務階段；Initial表示無人機處于初始階段；Kv,ini為初始階段速度協同系數。

經過一段時間調整后，無人機個體間距進入合理區間，集群便進入協同運動階段。為此需指定集群中少數無人機作為領導者，享有目標軌跡信息；而其他無人機作為跟隨者，通過對其鄰居狀態的感知，最終實現對于領導者的跟隨。

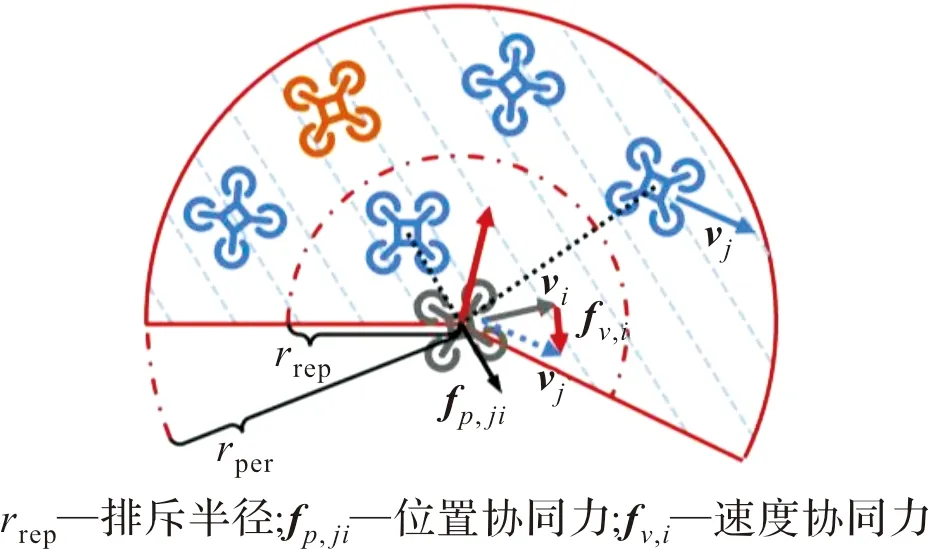
圖3 無人機集群協同運動階段交互機制

需要說明的是除被委派為領導者的無人機外，其余無人機對于領導者并不知情，即僅能通過對于周圍無人機的感知進行期望狀態指令的計算；而領導者則僅根據期望軌跡進行運動，不再考慮位置以及速度協同。在此假設下速度協同力設計如式(8)，類似的運動階段速度協同力的設計同樣要考慮距離影響因素，由于取消了吸引區，因此在對齊區遠端需保證速度協同力較大以防止群體發散，并且在位置協同力的作用下，大部分鄰居處于對齊區內，因此還需要考慮中心個體與鄰居速度大小偏差的權重因素，即優先考慮速度大下偏差較大的鄰居個體。

(8)

式中：fv,ji為無人機j對無人機i的位置協同力；Kv,move為運動階段速度協同系數。

3 仿真驗證

基于以上有限交互機制的設計，現對其有效性進行仿真驗證。假設無人機集群數量n=100，初始情況下,無人機靜止并隨機分布于以原點為中心，體積為20 m×20 m×20 m的立方體中。仿真總長tall=60 s，迭代步長Δt=0.02 s。

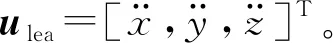
(9)

(10)

式中：T為完成一次期望8字軌跡的周期，具體仿真參數如表1所示。

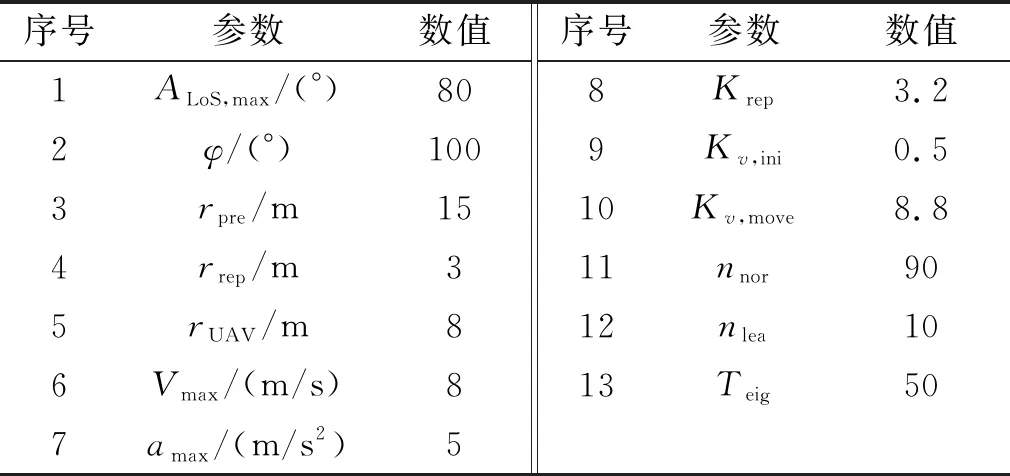
表1 仿真主要參數列表

利用所設計的有限交互規則對無人機集群的運動進行仿真驗證，具體結果如圖4所示。

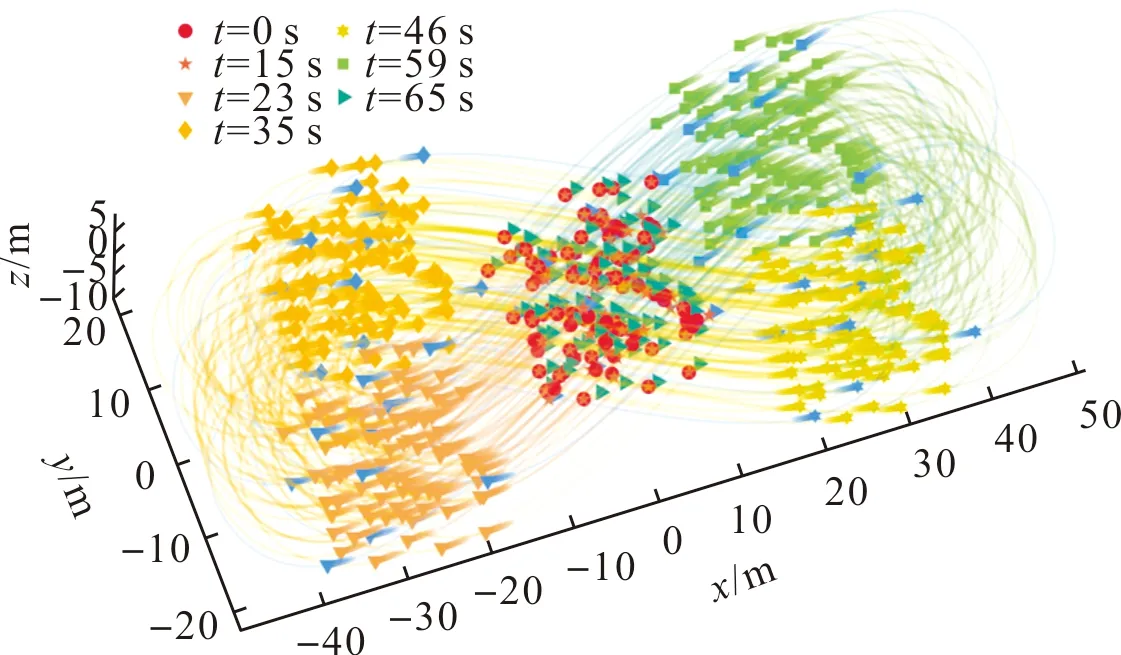
圖4 無人機集群運動軌跡

圖4為仿真全過程無人機集群的運動軌跡。通過全局視圖可以很直觀地說明：集群整體能夠在少數領導者(nnor∶nlea=9∶1；領導者為途中淡藍色個體)引導下完成對于期望軌跡的跟隨。在軌跡中的拐點位置，集群能夠較好地協同轉彎，不會產生拐彎處個體脫群現象，說明所設計的運動速度協同力很好地起到速度協同的作用。對于初始情況下位置安全性的獲取從圖中也可以看出，一些無人機存在一定位移以獲取位置安全性。同時，當無人機間距得到滿足時，初始速度協同力也能夠很好地起到減速作用以保持此刻的安全狀態。

圖5表示無人機集群在飛行過程中個體間最短距離的變化情況。首先，在初始階段由于位置的隨機初始化，存在個體間間距明顯小于安全距離的情況(此安全距離表示無人機空間半徑，即rUAV=2 m)。在所設計的位置協同力(即排斥力)的作用下，短時間內即可實現無人機間距的安全化；其次，在無人機協同運動時，由于領導者并不考慮其他個體的狀態，因此會造成一定的間距縮短。20～40 s時段，個體間距存在明顯縮短，但在位置協同力的作用下，個體間距保持在合理且安全的范圍內，證明所設計的位置協同力有效。

圖5 無人機集群飛行過程中個體最短間距變化

圖6表示集群運動過程中全部個體的速度變化情況。初始情況下，無人機個體在初始速度協同力的作用下，在滿足安全性后減速并懸停；在開始協同運動后，由于領導者自身運動狀態變化完全來自于期望軌跡參數，而普通個體速度變化則來自對其鄰居的感知，因此信息傳遞的延遲作用造成了普通個體相較領導者速度變化存在一定的滯后，但此滯后并不影響集群整體的協同運動效果，因此所設計的速度協同力有效。

為定量分析集群協同運動效果，對領導者與普通個體的速度進行平均化差異處理，即考慮協同運動過程中兩類無人機平均速度的差異，具體如式(11)～式(12)所示：

(11)

(12)

圖7表示集群運動過程中平均速度大小及方向的偏差變化情況。結合圖6分析，15～20 s期間運動起步，由于普通個體的滯后性，速度大小偏差會先逐步增大，然后在速度協同力的作用下逐漸減小，直至20 s左右開始進入第一個轉彎，由于信息傳遞的滯后性，速度大小偏差會先增大，經協同力作用減小，同理可以分析后續現象。對于平均速度方向偏差，初始時偏差較大，隨著速度協同力的作用基本可以維持偏差在較小范圍內波動，證明所設計的速度協調力在方向上的控制作用比較明顯且更為有效。

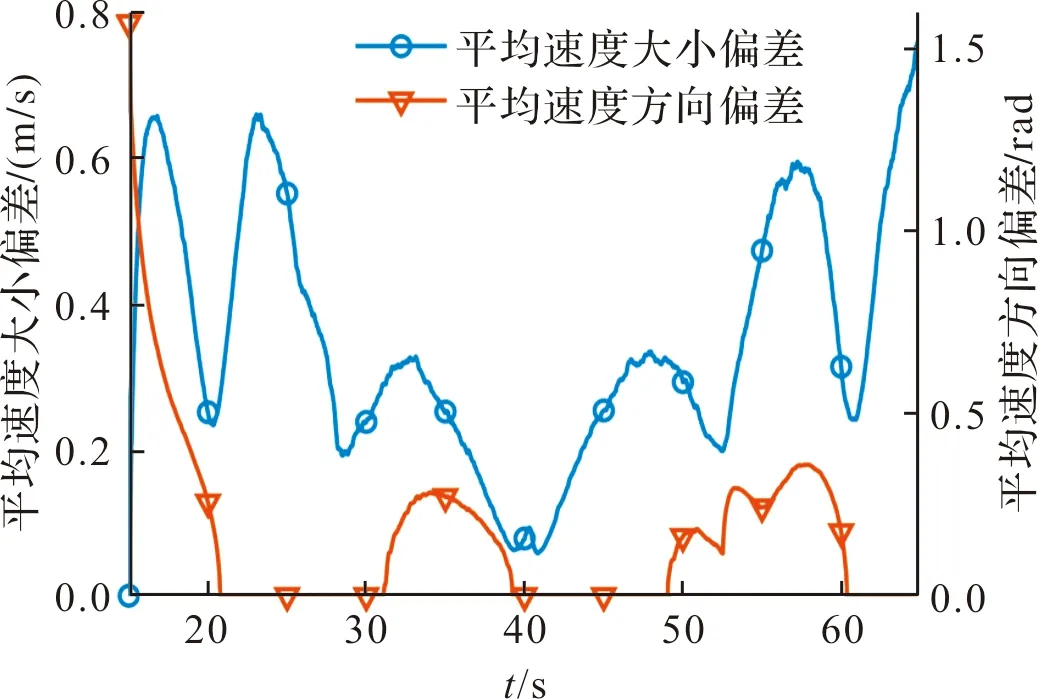
圖7 無人機集群協同運動性能評估

4 結論

提出了一種應用于無人機集群控制的有限交互規則，分別設計了有效交互和交互機制，并通過仿真分析驗證了在該規則下無人機集群能夠實現沿指定軌跡的協同運動，且在過程中保證了個體間的安全性。為工程化應用，針對集群規模、領導者比例等應用中可變因素，對方法有效性的具體影響，將是后續研究中的重點。