不同設計參數對矮塔斜拉橋受力及變形的影響研究

作者簡介：

陳金梅（1983—），工程師，主要從事建設管理工作。

摘要：文章以某雙塔混凝土矮塔斜拉橋為研究對象，通過運用Midas Civil有限元軟件建立實橋數值模型，對不同主梁剛度比、邊中跨比、無索區長度情形下斜拉橋的主梁受力及變形影響規律進行研究。結果表明：（1）隨著主梁剛度比的增大，矮塔斜拉橋主梁中跨、邊跨的最大撓度均逐漸減小，而主梁中跨、邊跨的最大彎矩逐漸增大，但主梁邊跨彎矩增幅不明顯;（2）矮塔斜拉橋主梁邊跨的最大撓度、最大彎矩均隨著邊中跨比的增大逐漸增大，而中跨的最大撓度、最大彎矩則隨之逐漸減小，且中跨的最大彎矩減幅緩慢;（3）隨著邊跨無索區長度的增大，矮塔斜拉橋邊、中跨最大撓度和最大彎矩均逐漸增大，但邊跨彎矩增長幅度不明顯。

關鍵詞：矮塔斜拉橋;主梁剛度比、邊中跨比、無索區長度;變形;受力

中國分類號：U448.27A361323

0 引言

由于矮塔斜拉橋具有跨距靈活、外形美觀、施工簡捷、經濟合理等優點，故在我國橋梁工程建設中得到廣泛的應用[1]。據調查統計，現有部分矮塔斜拉橋因早期設計考慮不足，使得橋梁產生了變形、受力不均等病害，而如何有效保證矮塔斜拉橋的安全穩定，成為現階段橋梁設計工作者需要重點考慮的課題[2-4]。

近年來，國內外學者在斜拉橋設計問題方面進行了大量的研究，如鮑英基等[5]對PC斜拉橋運營階段主梁的應力和位移進行敏感性分析，得出主梁應力和位移隨各參數的變化規律，為該橋梁運營養護管理提供借鑒和參考;牛偉迪[6]以神農湖大橋為研究對象，闡述了獨塔斜拉橋的總體設計思路，分別對主橋整體與索塔錨固系統展開了靜力分析，認為該橋的索塔錨固系統設計合理且整體結構滿足規范要求;衛康華等[7]通過計算比較各設計參數在成橋狀態時對主梁線形、應力、成橋索力和主塔偏位的影響，發現主梁容重、拉索初張力、季節溫差和索梁溫差為主要設計參數，而混凝土彈模、日照溫差和索塔兩側溫差對成橋狀態的影響較小，為次要參數;李德旭等[8]采用有限元分析方法，設計了4種主塔橫梁設置方案，從斜拉索受力、主梁變形及應力、主塔變形及應力方面進行定性分析，發現混凝土無背索斜拉橋主塔上橫梁的設計十分必要。考慮到有關矮塔斜拉橋設計參數的影響研究較為欠缺，筆者以某矮塔斜拉橋為研究背景，通過借助Midas Civil有限元軟件，分別對不同設計參數情形下的矮塔斜拉橋受力及變形規律進行了系統研究，以期為同類矮塔斜拉橋工程的設計工作提供參考與借鑒。

1 項目概況

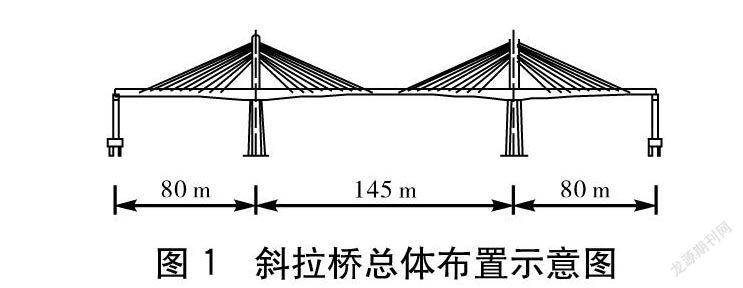
某雙塔混凝土矮塔斜拉橋跨徑為（80+145+80） m，橋寬為25.25 m，其中包括行車道寬為2×11.25 m，防撞護欄寬為2×0.5 m，中央隔離帶寬為2 m。橋梁車道采用雙向六車道設計，設計速度標準為80 km/h，設計荷載為公路-Ⅰ級。該斜拉橋上部結構采用單箱三室斜腹板變截面箱梁，其頂板、底板分別寬為12 m和6.8 m，支點處與跨中處梁高分別為5.8 m、2.8 m，在斜拉索張拉范圍處的箱梁內每隔6 m設有一厚度為0.4 m的橫隔板。該斜拉橋的主梁、塔間采用塔梁固結體系形式，主塔采用截面尺寸為5 m×2.4 m的矩形斷面，橋面以上塔高為24 m。主塔上17對斜拉索呈單索面扇形對稱布置，其梁與塔上間距分別為7 m、1 m，邊中跨無索區的長度分別為18 m、21 m。斜拉橋的整體布置情況如圖1所示。

2 有限元模型的建立

通過借助Midas Civil有限元軟件建立該矮塔斜拉橋的三維數值模型。模型中矮塔斜拉橋的梁、墩及主塔都采用梁單元進行模擬，而斜拉索則采用桁架單元進行模擬。實橋模型共劃分為240個單元、286個節點。斜拉橋實體模型如圖2所示。

有限元計算過程中斜拉索的初始張拉力取值為5 600 kN，而彈性模量則根據鋼絞線的實際彈性模量進行取值，考慮到防腐材料重量對斜拉索的影響，模型中斜拉索的容重按增加10%取值。模型中梁墩節點間剛接，梁塔節點間固結。計算荷載考慮恒載、溫載、掛籃與濕重荷載、活載及混凝土的收縮徐變等。鋼絞線與預應力鋼筋參數取值如表1所示。

3 結果與分析

矮塔斜拉橋的主要設計參數包括主梁剛度比、邊中跨比、邊跨無索區長度等，本文將上述參數作為控制變量，探討不同設計參數對矮塔斜拉橋受力及變形的影響規律。

3.1 主梁剛度比

通過建立主梁剛度比分別為0.2、0.6、1.0、1.4及1.8的矮塔斜拉橋模型，針對不同主梁剛度比的主梁邊、中跨撓度及彎矩進行計算，得到最大撓度及彎矩變化曲線如圖3所示。

根據圖3（a）可知，隨著矮塔斜拉橋主梁剛度比的增大，主梁邊、中跨的最大撓度均呈不斷減小的趨勢變化，說明主梁剛度比對矮塔斜拉橋變形的影響顯著。當主梁剛度比由0.2增至1.8時，主梁邊跨最大撓度由158 mm減小至56 mm，減幅達64.5%，而主梁中跨最大撓度由232 mm減小至85 mm，減幅達63.3%，說明增大主梁剛度比可以大幅度降低矮塔斜拉橋主梁邊、中跨變形量。由圖3（b）可知，隨著矮塔斜拉橋主梁剛度比的增大，主梁邊、中跨的最大彎矩均呈不斷增大趨勢變化，說明主梁剛度比對矮塔斜拉橋受力存在影響。當主梁剛度比由0.2增至1.8時，主梁邊跨最大彎矩由33 308 kN·m增至39 528 kN·m，增幅為18.7%，而主梁中跨最大彎矩由46 552 kN·m增至101 183 kN·m，增幅達117.3%，說明增大主梁剛度比會大幅度增加矮塔斜拉橋主梁中跨受力，不利于結構安全性。

3.2 邊中跨比

為研究邊中跨比對矮塔斜拉橋受力及變形的影響，選取邊中跨比分別為0.52、0.54、0.56、0.58及0.6，針對不同邊中跨比的斜拉橋有限元模型進行受力及變形分析，得到最大撓度與彎矩計算結果如圖4所示。

由圖4（a）可知，矮塔斜拉橋主梁邊跨的最大撓度隨著邊中跨比的增大呈逐漸增大變化趨勢，而中跨的最大撓度則隨之呈減小變化，表明矮塔斜拉橋的結構變形受邊中跨比的影響較大。在邊中跨比為0.52時，主梁邊跨的最大撓度為82 mm，當邊中跨比增至0.6時，邊跨最大撓度達118 mm，增幅為43.9%;在邊中跨比為0.52時，主梁中跨的最大撓度為125 mm，當邊中跨比增至0.6時，中跨最大撓度減至106 mm，減幅為15.2%，說明邊中跨比的增大在一定程度可以減小主梁中跨變形，但同時也導致邊跨的變形大幅增加。根據圖4（b）可知，斜拉橋主梁邊跨的最大彎矩隨著邊中跨比的增大呈逐漸增大的變化趨勢，而中跨的最大彎矩則隨之呈緩慢減小變化，表明邊中跨比在一定程度上對斜拉橋的結構受力存在影響。在邊中跨比為0.52時，主梁邊跨的最大彎矩為16 850 kN·m，當邊中跨比增至0.6時，邊跨最大彎矩達108 887 kN·m，增幅為546%;在邊中跨比為0.52時，主梁中跨的最大彎矩為87 528 kN·m，當邊中跨比增至0.6時，中跨最大彎矩減至83 999 kN·m，減幅僅為4%，說明邊中跨比的增大會導致斜拉橋的主梁邊跨受力增加，不利于橋梁結構安全。

3.3 邊跨無索區長度

通過建立無索區長度分別為18 m、24 m、30 m、36 m及42 m的矮塔斜拉橋有限元模型，針對不同無索區長度的橋梁邊、中跨撓度及彎矩進行計算，得到最大撓度及彎矩變化曲線如圖5所示。

根據圖5（a）可知，矮塔斜拉橋邊、中跨最大撓度均隨著邊跨無索區長度的增大而不斷增大，說明邊跨無索區長度對矮塔斜拉橋變形的影響較大。當無索區長度由18 m增至42 m時，主梁邊跨最大撓度由82 mm增至405 mm，增幅為394%，而中跨最大撓度由118 mm增至457 mm，增幅為287%，說明增大無索區長度會大幅度提升主梁邊、中跨的變形量。由圖5（b）可知，隨著矮塔斜拉橋邊跨無索區長度的增大，主梁邊、中跨最大彎矩均呈不斷增大趨勢變化，說明無索區長度對矮塔斜拉橋受力存在影響。當無索區長度由18 m增至42 m時，主梁邊跨最大彎矩由38 412 kN·m增至42 278 kN·m，增幅為10.1%，而主梁中跨最大彎矩由86 568 kN·m增至104 257 kN·m，增幅為20.4%，說明增大邊跨無索區長度會在一定程度上增大矮塔斜拉橋整體結構受力。

4 結語

本文以某矮塔斜拉橋為研究背景，分別研究了不同主梁剛度比、邊中跨比、無索區長度對主梁受力及變形的影響規律，得到以下結論：

（1）隨著主梁剛度比的增大，矮塔斜拉橋主梁中跨、邊跨的最大撓度均逐漸減小，而主梁中跨、邊跨的最大彎矩逐漸增大，且主梁邊跨彎矩增幅較小。

（2）矮塔斜拉橋主梁邊跨的最大撓度隨著邊中跨比的增大逐漸增大，而中跨的最大撓度則逐漸減小;斜拉橋主梁邊跨的最大彎矩隨著邊中跨比的增大逐漸增大，而中跨的最大彎矩則隨之緩慢減小。

（3）隨著邊跨無索區長度的增大，矮塔斜拉橋邊、中跨最大撓度均逐漸增大;隨著邊跨無索區長度的增大，斜拉橋主梁邊、中跨最大彎矩均呈不斷增大變化，但邊跨彎矩增長幅度較小。

參考文獻：

[1]申 磊，胡 鋒，崔文濤.某大跨徑雙塔單索面矮塔斜拉橋動載試驗研究[J].公路，2021，66（2）：124-128.

[2]楊德厚，鄧同生，李順波.矮塔斜拉橋塔梁同步施工階段塔梁墩固結部位局部應力分析[J].交通科技，2021（2）：28-33.

[3]曹發源.矮塔斜拉橋塔跨比的優化研究[J].北方交通，2020（4）：34-37.

[4]李紅豫，李 恒，吳 悅，等.基于BIM的東洲湘江大橋參數化設計應用研究[J].公路，2020，65（11）：173-178.

[5]鮑英基，蔣斌松，李文斌.PC矮塔斜拉橋運營階段參數敏感性分析[J].公路，2020，65（8）：216-222.

[6]牛偉迪.異型鋼結構單塔寬幅箱梁斜拉橋設計分析[J].中國市政工程，2021（2）：22-25，123.

[7]衛康華，羅 浩，楊孟剛.塔墩梁固結的三塔四跨矮塔斜拉橋成橋狀態力學參數研究[J].鐵道科學與工程學報，2017，14（5）：988-996.

[8]李德旭，喬文靖，彭晶蓉.斜拉橋主塔橫梁設計參數對結構靜力性能的影響[J].中國公路，2020（3）：100-101.

3783501908275