基于神經網絡反演溫度場的燃機余熱鍋爐汽包有限元分析

張毅樂 傅洪軍 王 瑾 俞洪鋒 葉篤毅

（1.浙江大學化工機械研究所；2.溫州燃機發電有限公司）

在發電設備中，汽包作為循環鍋爐的重要承壓部件，是工質加熱、蒸發和過熱3個過程的連接樞紐［1］。汽包在啟停和變負荷運行時，由于內部工質溫度變化，在汽包筒體與各連接管接頭處往往會引入較大的溫度梯度，因此汽包結構的溫度場與熱應力分析已成為鍋爐汽包安全性評價的重要內容之一。

目前，工程中對汽包溫度場的計算主要采用直接解法［2～5］與反推解法［6～10］。其中，直接解法是利用邊界條件對導熱微分方程直接求解。 例如，王麗媛使用工質溫度作為汽包內壁壁溫進行了汽包的溫度場分析［2］；李勇等采用第三類邊界條件分析了某汽包的溫度場［3，4］；賈鴻祥和林友新的研究發現，汽包內壁直接采用工質溫度作為邊界條件會引入較大誤差［5］。然而，直接解法通常要求對汽包進行開孔布置內壁溫度測點，這不僅會增加成本，也會引入安全隱患［11］。 反推解法則是利用汽包外壁測點對汽包溫度場進行反推計算。 例如，Taler J等利用空間行進法反演了汽包溫度場［6～8］；史良宵使用正反問題耦合解法重構了鍋爐的溫度場［9］；Wang X等利用自適應卡爾曼濾波對汽包溫度進行了在線監控［10］。 但現有的反推解法數學模型較為復雜， 需要較多的外壁溫度測點，在工程中也難以實現。

近年來，隨著計算機技術的發展，智能優化算法（如BP神經網絡）已被越來越多地應用于導熱反問題的求解中［12～15］，主要涉及凝固界面換熱系數的研究［13］與機床換熱系數反演［15］，但對于鍋爐汽包換熱系數反演的研究卻鮮有報道。 在此，筆者以某電廠9E燃機聯合循環機組余熱鍋爐汽包為對象， 利用BP神經網絡結合實測溫度數據，開展汽包內壁換熱系數的反演求解，并結合有限元法研究熱態啟動下余熱鍋爐汽包的瞬態溫度場和應力場，為后續余熱鍋爐汽包安全性評價提供理論分析基礎。

1 余熱鍋爐汽包簡介

余熱鍋爐汽包結構如圖1所示， 汽包材料選用15NiCuMoNb5， 筒體內徑2 420 mm， 厚度40 mm。 筒體上連接2個蒸汽入口管（?355.6 mm×15.9 mm）、2 個蒸汽出口管（?355.6 mm ×15.9 mm）、1個下降管（?457.4 mm×19.05 mm）和1個給水管（?219.1 mm×12.7 mm），接管管座材料選用15NiCuMoNb5，接管材料選用SA106B。

圖1 余熱鍋爐汽包結構示意圖

表1列出了不同溫度下汽包相關材料的主要物理與力學性能［16］。

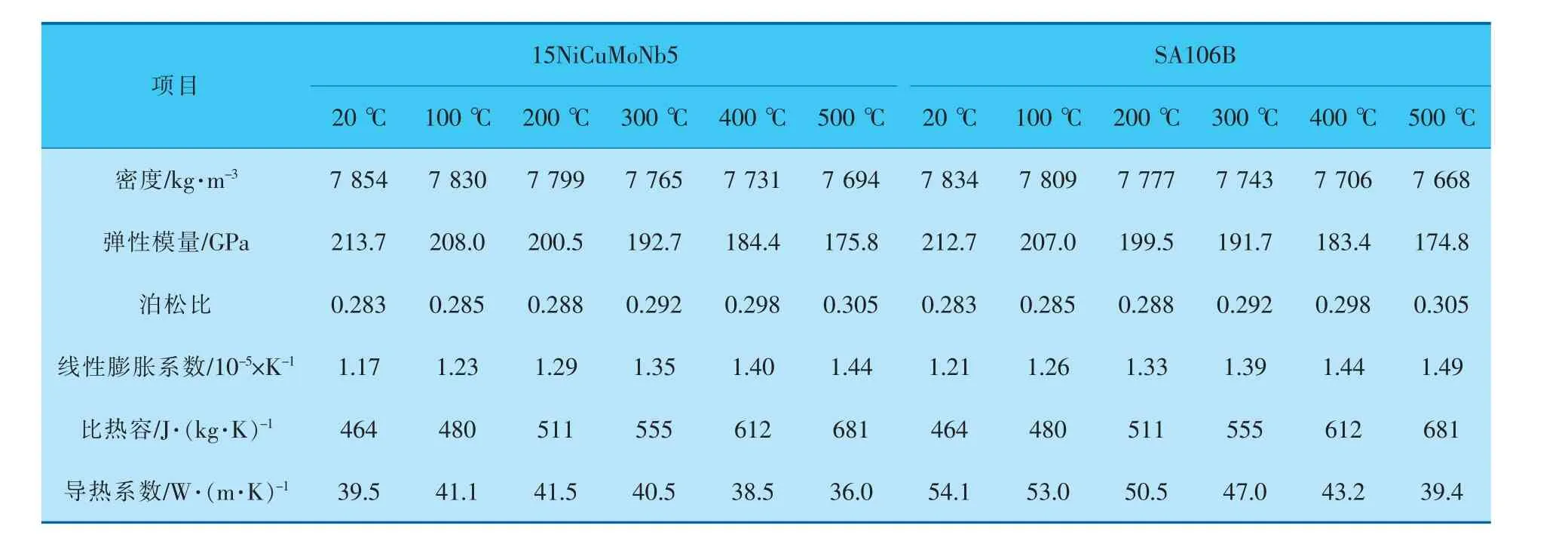
表1 不同溫度下汽包相關材料的主要物理與力學性能

圖2是余熱鍋爐熱啟動過程中汽包內部水溫、壓力和水位監控值隨時間的變化歷程。

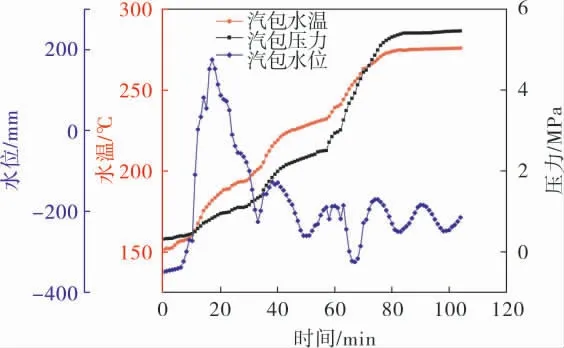
圖2 余熱鍋爐熱啟動過程中汽包主要熱力參數隨時間的變化歷程

2 基于人工神經網絡的汽包內壁換熱系數反演方法

對于實際服役的鍋爐汽包，由于受形狀、材料性能及內部工質等多種因素的影響， 外壁測點溫度T=［T上壁測點，T下壁測點］與內壁對流換熱系數h=［h水側，h汽側］之間是一個復雜的非線性函數，采用常規數學方法很難建立兩者之間的確定性關系。采用人工神經網絡， 通過不斷學習調整輸入層與隱藏層和隱藏層與輸出層單元間聯系的權值，可以構建兩者間的映射， 從而達到利用外壁測點溫度反推求解內壁換熱系數的目的。圖3給出了汽包外壁上/下壁測點溫度T=［T0，T1］ 與內壁對流換熱系數h=［h0，h1］之間的單隱藏層BP神經網絡結構，圖中W=［W00，…，W0m，W10，…，W1m］為輸入層與隱藏層之間的權值向量；f0， …，fm為m個隱藏層神經元；W′=［W′00，…，W′0m，W′10，…，W′1m］為隱藏層與輸出層之間的權值向量。 基于上述BP神經網絡反推算汽包內壁換熱系數可按以下3個步驟進行：

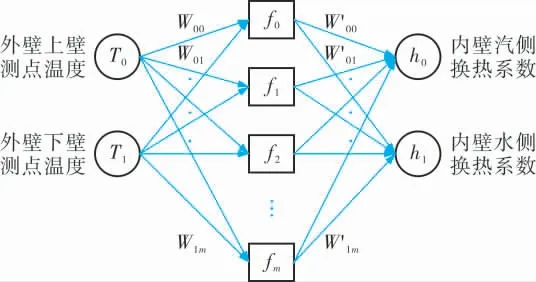
圖3 汽包外壁上/下壁測點溫度與內壁對流換熱系數之間的單隱藏層BP神經網絡結構

a. 網絡訓練。由于啟動過程汽包內壁換熱系數隨時間變化， 根據Beck J V提出的連續指定函數法［17］，將啟動過程換熱系數按同一個時間間隔分成多個瞬時值，利用神經網絡反求每個時間間隔內的換熱系數。 將多組內壁換熱系數與對應的外壁測點溫度模擬值組成訓練樣本，并對網絡進行訓練。 訓練樣本由500組內壁汽水側換熱系數與對應的外壁上/下壁溫度模擬值構成，按7∶2∶1的比例劃分訓練集、測試集與驗證集。 換熱系數范圍為50～5 000 W/（m2·℃）。

b. 換熱系數預測。將啟動過程中外壁測點溫度記錄值作為輸入值， 利用步驟a中訓練合格的神經網絡對汽包實際內壁汽水側換熱系數進行預測。

c. 結果驗證。 將步驟b中神經網絡預測出的內壁換熱系數進一步結合三維有限元模型進行計算，得到外壁溫度測點處模擬值，并與實測值進行比較。 如果溫度模擬值精度未達到要求，則重復步驟a、b。

圖4為采用神經網絡結合熱啟動過程汽包外壁測點溫度反演得到的汽包內壁換熱系數時間變化歷程。 由圖4可以看出：隨著啟動過程的進行，由于汽包中蒸汽壓力升高，產汽量增加，汽側換熱系數顯著增大； 由于汽水之間熱交換導致下部水溫不斷升高，體積不斷膨脹，水側換熱系數也有一定程度的增加；在啟動末期，由于汽包內部換熱趨于穩定，汽側和水側換熱系數均有所減小。

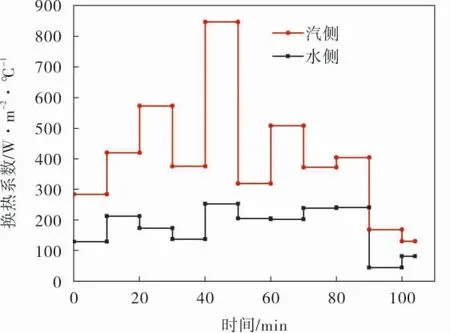
圖4 神經網絡結合熱啟動過程汽包外壁測點溫度反演得到的汽包內壁換熱系數時間變化歷程

3 余熱鍋爐汽包有限元分析

3.1 汽包有限元模型

在余熱鍋爐汽包有限元建模時，主要考慮蒸汽入口管、蒸汽出口管、下降管及給水管等主要部件的影響。 對上述接管進行“截斷”時，主要考慮接管吊架約束，并使接管“截斷”長度大于相應的邊緣應力衰減長度［18］。 本次余熱鍋爐汽包的出口管（入口管）、給水管與下降管截斷位置為圖1a中的A-A、B-B和C-C。 有限元網格熱分析時選擇Solid90單元，結構分析時選擇Solid186單元。 為了提高有限元分析精度，沿汽包壁厚劃分5層，筒體和接管網格采用掃掠和六面體網格相結合的劃分方式，在結構不連續處進行網格加密。 汽包的有限元模型（圖5）包括353 568個單元和1 452 924個節點。

圖5 汽包有限元模型

由于汽包外壁覆蓋有較厚的保溫層，其溫度邊界可視為絕熱處理。 汽包內壁采用第三類邊界條件，以水位作為分界線將汽包分為上半部分汽側與下半部分水側。 汽包內壁汽側與水側換熱系數采用圖4所示的基于神經網絡反演得到的結果。

汽包有限元分析時的載荷主要包括溫度載荷、蒸汽壓力、汽包自重和支吊架、下降管支座、鞍座墊板、底板的位移約束。 各接管截斷口施加等效拉力模擬截斷前管系的軸向拉力，計算式如下［19］：

式中 di、do——接管的內、外直徑，m；

Pc——截斷截面上均勻分布的拉應力，Pa；

pi——汽包的內壓，Pa。

3.2 有限元分析結果

3.2.1 汽包瞬態溫度場

圖6為熱態啟動過程某一時刻汽包筒體和各接管部位的瞬態溫度場。 從圖6a可見，汽包壁在啟動過程中存在徑向溫度梯度和周向溫度梯度，其中水位線處發生較大溫度變化（圖中箭頭所指處）。 汽包最大溫度主要出現在汽側內壁，水側外壁溫度相對較低。 這是由于啟動過程中汽包汽側內壁換熱系數較水側大，傳熱更快。 接管管座處由于厚度較厚，相應的徑向溫度梯度較大（圖6b～e）。

圖6 熱態啟動過程某一時刻汽包筒體和各接管部位的瞬態溫度場

將啟動過程部分時刻汽包溫度測點處的模擬值與實測值進行比較，結果列于表2。 由表2可知， 上壁溫度模擬值與實測值的相對誤差在0.781%以內，下壁溫度模擬值與實測值的相對誤差在1.108%以內。 由此表明：應用神經網絡反演內壁換熱系數能夠反演汽包的瞬態溫度場。

表2 啟動過程部分時刻汽包上、下壁溫度模擬值與實測值及其相對誤差

3.2.2 汽包瞬態應力場

將上述汽包溫度場作為載荷條件輸入，模擬汽包啟動過程的瞬態應力場。 圖7是啟動過程78.7 min時汽包的應力分布以及各接管的局部應力場， 圖7b～e中A點是相應接管的最大等效應力部位。 由圖7可知，在汽包接管與筒體連接肩部的內拐點處（A點）應力較大，即該處存在應力集中現象。

圖8a給出了各接管危險點（A點）的等效應力隨汽包啟動過程的變化特征。 由圖8a可看出，在汽包啟動過程中， 各接管危險點等效應力均呈單調遞增的現象，并在啟動結束時（約104 min）達到最大值。 其中，蒸汽出口管與蒸汽入口管最大等效應力基本一致， 均明顯大于下降管與給水管的最大等效應力。進一步計算A點處徑向應力、周向應力、軸向應力與筒體周向薄膜應力的比值（JB 4732—1995 中稱該比值為應力指數［20］，表示該位置在僅受內壓下的應力集中程度）。 圖8b給出了各接管A點處應力指數隨啟動過程的變化特征。 從圖8b中可以看出，余熱鍋爐汽包各接管A點處的應力集中主要來自周向應力的貢獻，對于下降管和給水管，由于內伸形式A點還存在較大的徑向應力。周向與徑向應力指數在啟動初期（50 min之前）變化較大，在啟動后期逐漸趨于平緩。 這是由于汽包啟動初期蒸汽壓力較小，熱應力是導致應力集中的主要因素，而在啟動后期， 主要是蒸汽壓力引起的應力集中。

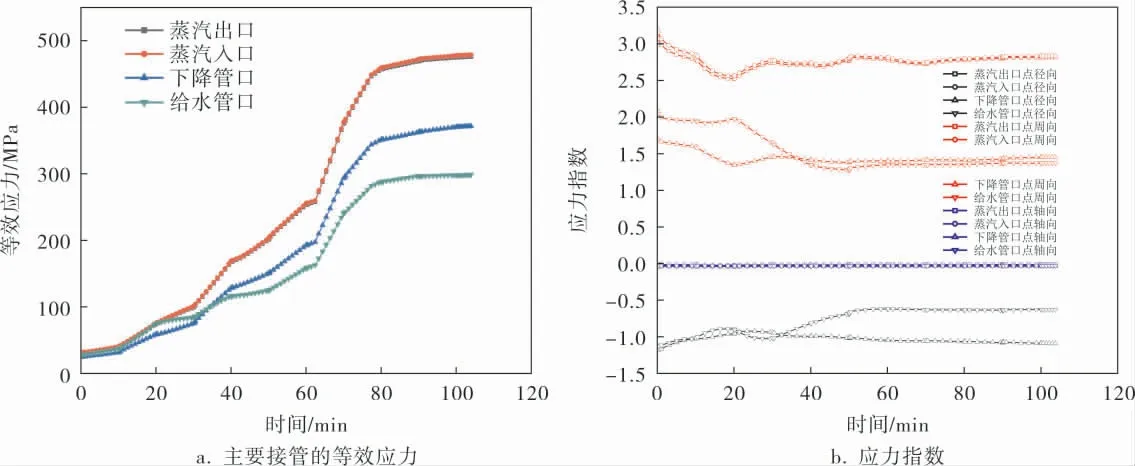
圖8 啟動過程汽包主要接管危險點等效應力與應力指數變化特征

4 結論

4.1 提出了一種基于人工神經網絡結合汽包外壁實測溫度反演汽包內壁瞬態換熱系數的方法。

4.2 應用有限元法， 結合汽包內壁換熱系數，模擬獲得了某燃機余熱鍋爐汽包筒體與主要接管處的瞬態溫度場，并通過汽包外壁溫度的模擬值與實測值進行比較得出兩者一致性較好。

4.3 分析余熱鍋爐汽包瞬態應力場，獲得各接管危險點處等效應力隨汽包啟動過程的變化特征。結果表明：汽包蒸汽出口管與蒸汽入口管最大等效應力基本一致，均大于下降管與給水管的最大等效應力；熱應力在啟動初期對總應力分布影響較大。

【致謝】本工作得到了浙江省能源集團有限公司科技項目（ZNKJ-2020-061）的支持。