雙切向環流憋壓式氣體分布器流動特性的數值模擬

余 帥 厲彥忠 劉景武 洪 坤 張建松

（1.西安交通大學能源與動力工程學院；2.浙江智海化工設備工程有限公司）

隨著大孔隙率、低壓降、新型高效填料的開發和大直徑、淺床層、低液氣比填料塔的發展，特別是對于高真空精餾過程，填料塔內氣流的初始分布、壓降等因素對填料塔的分離效率有著重大影響［1～3］，許多研究學者對精餾塔內不同類型氣體分布器的流動規律進行較為全面的研究。 杜明通過搭建試驗臺對精餾塔內雙列葉片式氣體分布器進行研究［4］；唐建峰等通過搭建試驗臺對FLNG填料塔內雙切向環流式氣體分布器進行研究［5～7］；金紅杰等通過數值模擬方法對精餾塔內環流式氣體分布器進行研究和優化［8～10］。 雖然目前研究得到氣體分布器模型的性能有所提升，但結構復雜， 在實際加工和生產應用中存在一定的難度，同時針對不同空分規模下氣體分布器的選型未形成相應的設計公式和規范，因此對設計和選型的指導極其有限。 在此，筆者通過數值模擬方法研究雙切向環流憋壓式氣體分布器的流動特性，并擬合得到適用于不同空分規模的氣體分布器尺寸參數及其與性能之間的函數影響關系，希望為氣體分布器的設計和選型提供一定的理論指導。

1 數值模擬方法

1.1 物理模型

以實際生產中應用的直徑4 000 mm的精餾塔用氣體分布器為模型，其主要結構參數如下：

分布器高度h 1 400 mm

塔徑D 4 000 mm

分布器內筒直徑d 3 080 mm

上塔壁高度h1600 mm

下塔壁高度h2800 mm

開孔尺寸（寬度K×高度L） 88 mm×500 mm

開孔數量 12

開孔位置分布角度 α=24°，β=60°

分流板高度h31 000 mm

分流板開口角度θ 120°

送風管直徑d11 000 mm

氣體分布器物理模型如圖1所示。

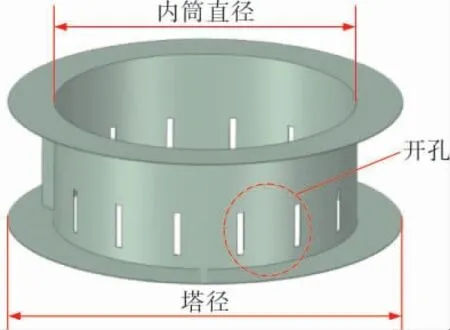
圖1 氣體分布器物理模型

1.2 數學模型

以氣體分布器內流場分布狀況為研究對象,該流場內流體行為為復雜的兩相三維湍流流動。鑒于實際情況的限制對模型作如下簡化：

a. 流體物性為實際運行時精餾塔下塔狀態對應的空氣物性參數；

b. 流體假定為單相流；

c. 模擬實際運行時精餾塔下塔的狀態，溫度取101 K，壓力取0.52 MPa，穩定流動，不可壓縮定常流動。

實際操作條件下，氣體在分布器內的流動是復雜的三維湍流流動。 因其在整個過程中的壓力變化不大， 因此把它當作不可壓縮氣體來處理。模擬中，流體流動情況近似為穩態流動。 整個過程可以用雷諾平均方程、湍動能和湍動耗散率輸運方程來描述。 進料口區域流體流型為充分發展的湍流。

連續性方程：

其中，常數C1=1.9，ε的有效普朗特數σε=1.2，ν為流體運動粘度。

1.3 邊界條件及其他設置

入口邊界條件：采用速度入口，結合工廠運行數據，設定氣體溫度為101 K，壓力為0.52 MPa，入口處中心速度4.99 m/s， 入口密度取該狀態下實際的氣體密度20.24 kg/m3，粘度7.4 μPa·s。

出口邊界條件：采用壓力出口條件，相對壓力設為0，操作壓力設為0.52 MPa。

壁面條件采用標準壁面函數進行計算。

計算采用FLUENT基于壓力的求解器， 湍流模型為Realizable k-ε模型，動量方程、湍動能和湍動耗散率方程采用一階迎風格式進行離散，對流項采用二階迎風格式［11］。 其中，各項收斂殘差均設為1×10-6。

1.4 氣體分布器性能評價指標

不均勻度和壓降是氣體分布器性能重要的設計和評價指標。

不均勻度λ的計算式為：

式中 pin——氣體入口截面壓力，Pa；

pout——氣體出口截面壓力，Pa。

1.5 模型驗證

在模型的劃分過程中采用了對稱面， 即對物理模型的半邊進行了網格劃分， 可有效減少計算量。 進行網格無關性驗證， 對壓降進行監控， 當壓降隨著網格數量的增加基本維持不變（不超過1%）時確定網格數量（圖2），網格數選擇750 000。

圖2 網格無關性驗證

為驗證所建模型的準確性， 建立文獻［5，6］中試驗裝置所用的氣體分布器物理模型，利用該物理模型進行數值模擬計算。 以不同入口速度下氣體分布器的壓降和出口截面上的不均勻度為考察對象，由表1和圖3可知：在出口截面上，氣體分布器不均勻度的模擬值與文獻試驗值之間平均絕對偏差為8.96%；在不同入口速度下，氣體分布器壓降的模擬值與文獻試驗值的變化趨勢相同，平均絕對偏差為14.40%。 綜上所述，可以認為筆者建立的數學模型能夠較好地預測氣體分布器不均勻度和壓降的變化趨勢。

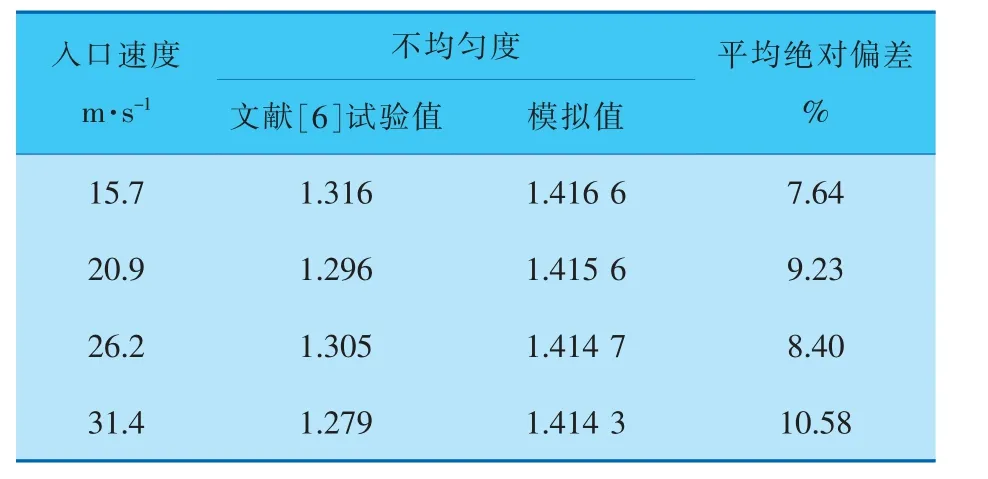
表1 不同入口速度下的不均勻度對比

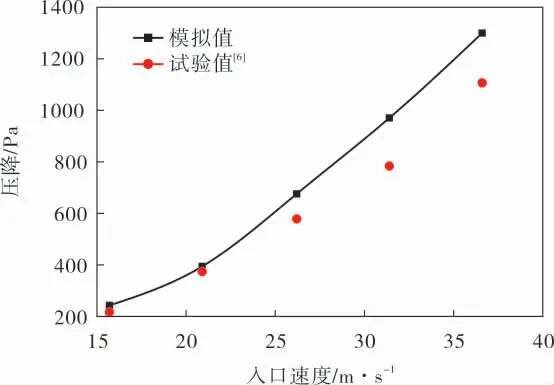
圖3 不同入口速度下的壓降對比

2 結果分析

2.1 流場分布特征

氣體分布器內氣體流動跡線及分布器出口軸向速度分布如圖4所示。 由圖4可以看出，氣體由入口進入氣體分布器環形通道，環流沿著環形通道向入口對側運動的過程中，經氣體分布器內筒壁上的導流孔噴射出去，從不同孔中噴射出的流體在遠離入口側匯合，匯合過程中大部分氣體向上運動，直至出口，另一部分氣體向氣體分布器底部流動，到達側壁后轉而向上流動至出口。

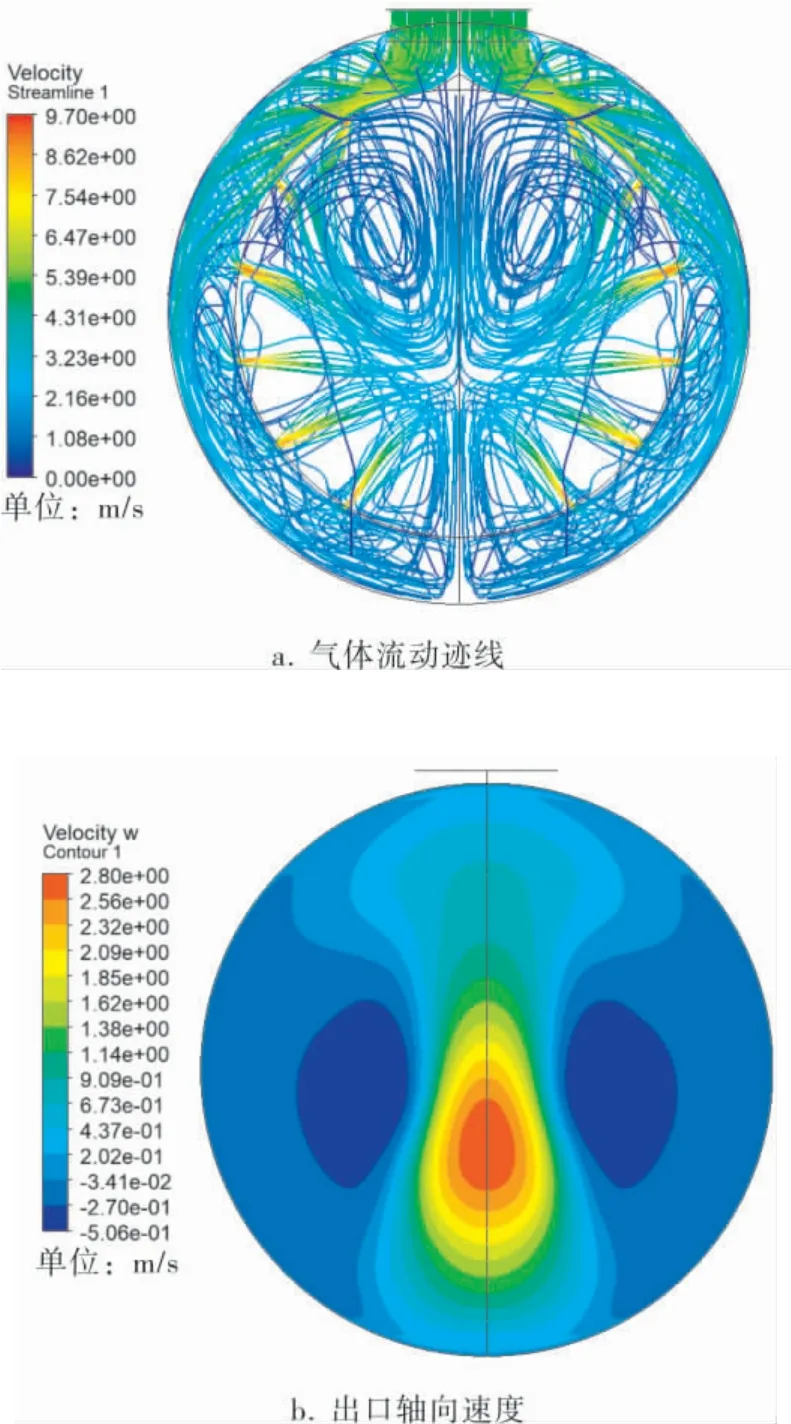
圖4 氣體分布器內氣體流動跡線及分布器出口軸向速度分布云圖

2.2 單參數影響規律

在保證氣體分布器上塔壁高度h1、 下塔壁高度h2、開孔數量、開孔位置分布角度α和β、分流板高度h3、分流板開口角度θ及送風管直徑d1等不變的基礎上，通過控制變量法分別計算得到氣體分布器高度h、開孔對比率?、徑比φ及塔徑D等對分布器性能的影響規律。

氣體分布器高度對其性能的影響規律如圖5所示。 由圖5可以看出：隨著氣體分布器高度的增加，壓降呈先減小后增大的趨勢，存在一個最佳高度使得壓降最小；不均勻度呈先增大后減小的趨勢，存在一個高度值使得不均勻度最大。

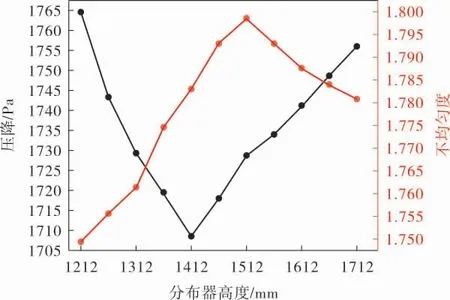
圖5 氣體分布器高度對其性能的影響規律

在研究氣體分布器性能隨開孔大小變化規律時，通過改變開孔寬度K來控制開口大小，但為了方便比較不同塔徑和分布器內筒直徑的情況，再定義一個結構參數——開孔對比率?， 其計算式為：

?=100%時為基本模型對應的尺寸。

在徑比φ=0.77的情況下， 不同塔徑氣體分布器性能隨開孔對比率的變化規律如圖6所示。 由圖6可以看出：隨著開孔對比率的增大，氣體分布器不均勻度大致呈線性減小的趨勢；壓降隨著開孔對比率的增大而減小， 且減小速度逐漸放緩；在徑比和塔徑相同的情況下， 開孔對比率從60%增至100%的過程中壓降減小幅度遠大于開孔對比率從100%增至200%的過程， 且二者之間近似呈非線性的二次函數規律變化。

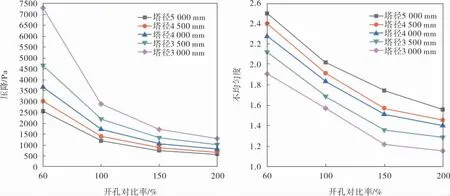
圖6 不同塔徑氣體分布器性能隨開孔對比率的變化規律

在研究氣體分布器性能隨氣體分布器內筒直徑變化規律時，為了方便比較不同塔徑和分布器內筒直徑的情況，定義一個結構參數——徑比φ，其計算式為：

φ=0.77時為基本模型對應的尺寸。

在?=100%的情況下， 不同塔徑氣體分布器性能隨徑比的變化規律如圖7所示。 由圖7可以看出：隨著徑比的增大，氣體分布器不均勻度大致呈線性減小的趨勢， 且開孔對比率較小 （60%～100%）時，其減小速度較緩慢；隨著徑比的增加，氣體分布器壓降有所減小， 且降低速度逐漸變緩。

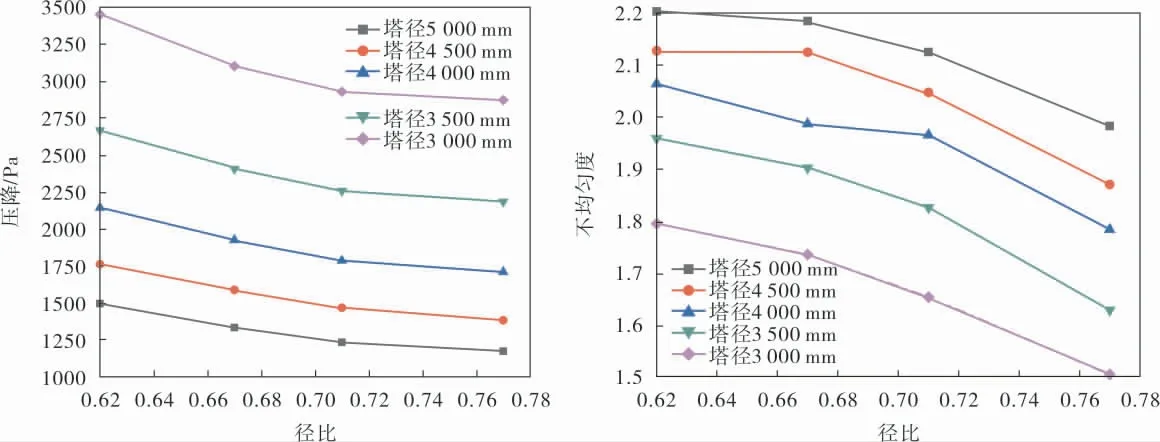
圖7 不同塔徑氣體分布器性能隨徑比的變化規律

保持開孔對比率不變，不同徑比氣體分布器性能隨塔徑的變化規律如圖8所示。 由圖8可以看出，隨著塔徑的增大，氣體分布器不均勻度大致呈線性增加的趨勢，壓降逐漸減小，近似呈非線性的二次函數規律變化，塔徑變化對氣體分布器壓降的影響大于對不均勻度的影響。

圖8 不同徑比氣體分布器性能隨塔徑的變化規律

由上述分析結果可知， 改變空分規模時，精餾塔塔徑、氣體分布器內筒直徑和開孔對比率這3個結構參數對氣體分布器性能起到決定性作用。

2.3 關聯式擬合

目前，在實際生產過程中，根據空分規模的不同，采用的精餾塔塔徑有所差異，氣體分布器規格也隨之變化。 筆者基于上述數值模擬結果，參考文獻［12］中的方法，采用CCD實驗點設計和響應面技術， 利用Design Expert軟件擬合得到氣體分布器壓降、不均勻度與主要結構參數的關聯式。 筆者選擇X1、X2、X3作為相應的變量，則有：

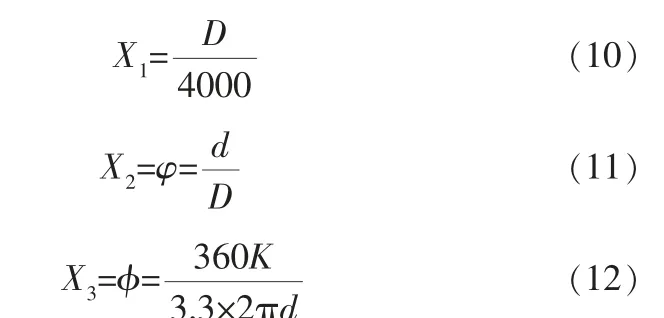
式（10）中的4 000表示基本模型的塔徑。對生成的響應面上得到的數據點進行氣體分布器性能關聯式擬合，可以得到：

不均勻度的擬合關聯式的擬合優度R2=0.988， 壓降的擬合關聯式的擬合優度R2=0.992。通過氣體分布器不均勻度和Eu的模擬計算值與擬合關聯式預測值的比較發現 （圖9），偏差都在±15%以內；不均勻度預測關聯式的最大偏差為7.48%；Eu預測關聯式的最大偏差為13.41%，表明筆者擬合得到的關聯式預測性能良好。

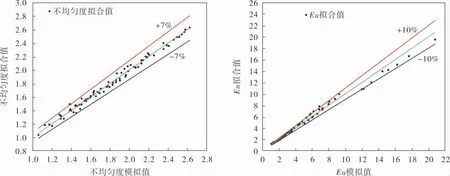
圖9 分布器性能擬合關聯式誤差

3 結論

3.1 采用CFD方法對雙切向環流憋壓式氣體分布器內氣體的流動進行了模擬計算，得到了分布器主要結構參數對分布器性能的影響規律，并擬合得到了分布器性能的擬合關聯式。

3.2 根據單參數影響計算，氣體分布器不均勻度與塔徑呈正相關，與分布器內筒直徑和開孔對比率呈負相關，隨著分布器高度的變化存在一個最大值；氣體分布器壓降與塔徑、分布器內筒直徑和開孔對比率呈負相關，隨著分布器高度的變化存在一個最小值。

3.3 通過Design Expert軟件利用響應面法得到了分布器的性能指標擬合關聯式，擬合得到的不均勻度和壓降預測關聯式的擬合優度分別為0.988和0.992， 擬合關聯式在結構參數變化范圍內是可靠的，能夠為不同空分規模用精餾塔氣體分布器的設計和選型提供參考。

【致謝】感謝盈德氣體集團有限公司及浙江智海化工設備工程有限公司在本文完成過程中提供的幫助與支持。