容器設計固化接管許用載荷計算方法研究

孫 浩

（中國原子能科學研究院）

容器和管道系統設計在核工程、化工及石油等領域應用廣泛，其中接管載荷常被確定用于解耦容器與管道系統設計。 容器設計需要考慮接管載荷對容器的影響，然而，在管道設計完成之前，最終的接管載荷是未知的。 工程實際應用中，則需要在完成容器和管道的設計前，約定一個合理的接管載荷限值，困難就在于很難針對每個特定容器接管制定一套最佳的接管載荷值。 若約定的接管載荷過低，管道設計可能會變得困難，設計成本過高；若約定的接管載荷過高，則設計容器接管處時需要采取不同程度的補強，而這將增加不必要的成本。

黃慶等針對核安全一級容器，給出核容器接管許用載荷的計算方法［1］；Mershon J L等于1984年在WRC 297公報上發表了在外載荷作用下圓柱殼接管局部應力計算［2］，該方法在很大程度上幫助設計人員解決了圓柱殼與接管連接結構中局部應力計算的問題［3，4］。 薛明德等采用修正的Morly方程，得到了適用于特定條件下的薄殼理論解［5］。 在全國鍋爐壓力容器標準化技術委員會和清華大學的支持下，根據清華大學工程力學系薛明德等歷經二十余年的科研成果，于2013年發布了指導性技術文件CSCBPV-TD001—2013 《內壓與支管外載作用下圓柱殼開孔應力分析方法》，對具有徑向平齊支管（接管）的圓柱殼（主殼，圓筒）開孔區，給出了內壓與支管外載荷作用下的應力分析工程計算方法［6］；徐君臣以在內壓與外載荷作用下的圓柱殼上一大開孔接管為例，采用有限元技術將計算結果與薄殼理論解進行了對比，為外載荷作用下接管應力分析提供一定參考依據［7］。

在工程設計中，容器的設計優先級一般要高于相連管道的設計優先級，故一般容器設計固化的時間要早于容器相連的管道系統。 管道系統易受土建施工、 設備采購及管道安裝施工等影響，常出現管道安裝完成前的現場澄清或設計變更，若最終的實際接管載荷超出設計階段約定的接管載荷，則需要容器設計者進行復核，但容器復核迭代用時長、人力成本高，故筆者針對設計固化的容器，尋求一種保守、高效的簡化計算方法，以完成對容器接管載荷的復核工作。

1 容器接管許用載荷簡化計算方法

1.1 容器設計固化

已設計固化的容器力學分析設計輸入包括容器設計圖紙、容器的技術規格書、材料性能參數、容器接管載荷、容器在各工況下的載荷數據（壓力、 溫度等） 及容器所在廠房的地震反應譜等；按照嚴格質量控制流程完成的正式出版的力學分析報告和完整的力學計算模型。

1.2 選取容器危險面

力學分析人員需要熟練地掌握力學分析方法和規范評價方法，并要對容器的結構設計有深入的認識。 根據已固化的容器成品設計文件和力學模型，即可選取由于接管載荷數值變化后可能引起的危險面，危險面的選取將直接影響最終的接管許用載荷，此類危險截面常出現在接管局部區、多個接管載荷共同影響區、支撐件及焊縫處等。

1.3 輸出各載荷下的應力結果建立數據庫

在已固化的容器力學模型上，根據容器評定規范的要求，輸出每個載荷（包括壓力、接管載荷及地震載荷等）作用下，每個危險截面的應力分析結果，并組建成載荷應力結果數據庫。 其中接管載荷的應力結果需要輸出容器上每個接管在局部坐標系上單位載荷的計算結果。

1.4 建立簡化計算表格

根據容器評定規范的要求，調用已建立好的數據庫，實現載荷間應力計算結果的自動組合疊加，此處的疊加方式采用線性疊加，并根據評定規范添加評定限值，通過計算應力值與評定限值的大小關系，可反向換算容器接管的許用接管載荷。 每個管口的接管載荷有3個力和3個力矩，由于在計算時采用的是線性疊加，6個載荷之間的比例關系默認固定不變，即反算的許用接管載荷也將與輸入載荷的比例關系一致。 當容器有多個接管時，多個接管的接管載荷彼此之間會產生影響，且對支撐件、焊縫等均可能產生影響，故換算得到的容器許用接管載荷為包括容器上所有管口的一組接管許用載荷。

2 算例分析

2.1 容器設計固化力學模型

容器為儲氣罐，設計時采用ASME［8］設計規范，核安全等級3級，設計溫度100 ℃，設計壓力1.5 MPa，無抗震要求，容器上所有焊縫均為全焊透焊縫。 容器設計參數如圖1a所示。 使用的有限元分析軟件為ANSYS，采用SOLID 186（高階3D20節點實體單元）單元建模［9，10］，單元數量181 902，節點數量804 503，有限元模型如圖1b所示。

圖1 儲罐有限元模型

2.2 危險截面選取

由于篇幅所限， 結合容器實際計算結果，選取5個危險截面， 每個危險截面按照A、B、C、D、E命名。 路徑劃分的數量與危險截面上實際模型的節點數量有關，在危險截面上將壁厚方向所有的節點路徑無遺漏地全部建立評定，此方法將人為的路徑選取評定工作簡化為機械式的命令流操作，在保證計算結果無遺漏的前提下，既能準確得到各應力分量的數值，又極大地提升了工作效率。 該算例在網格劃分時有所設置，每個危險截面上內壁與外壁剛好有160對節點， 故每個危險截面可以劃分160條路徑。A、B危險截面的路徑位置在1號接管處， 如圖2a所示；C、D危險截面路徑位置在2號接管處， 如圖2b所示；E危險截面路徑位置在支撐件根部，如圖2c所示。

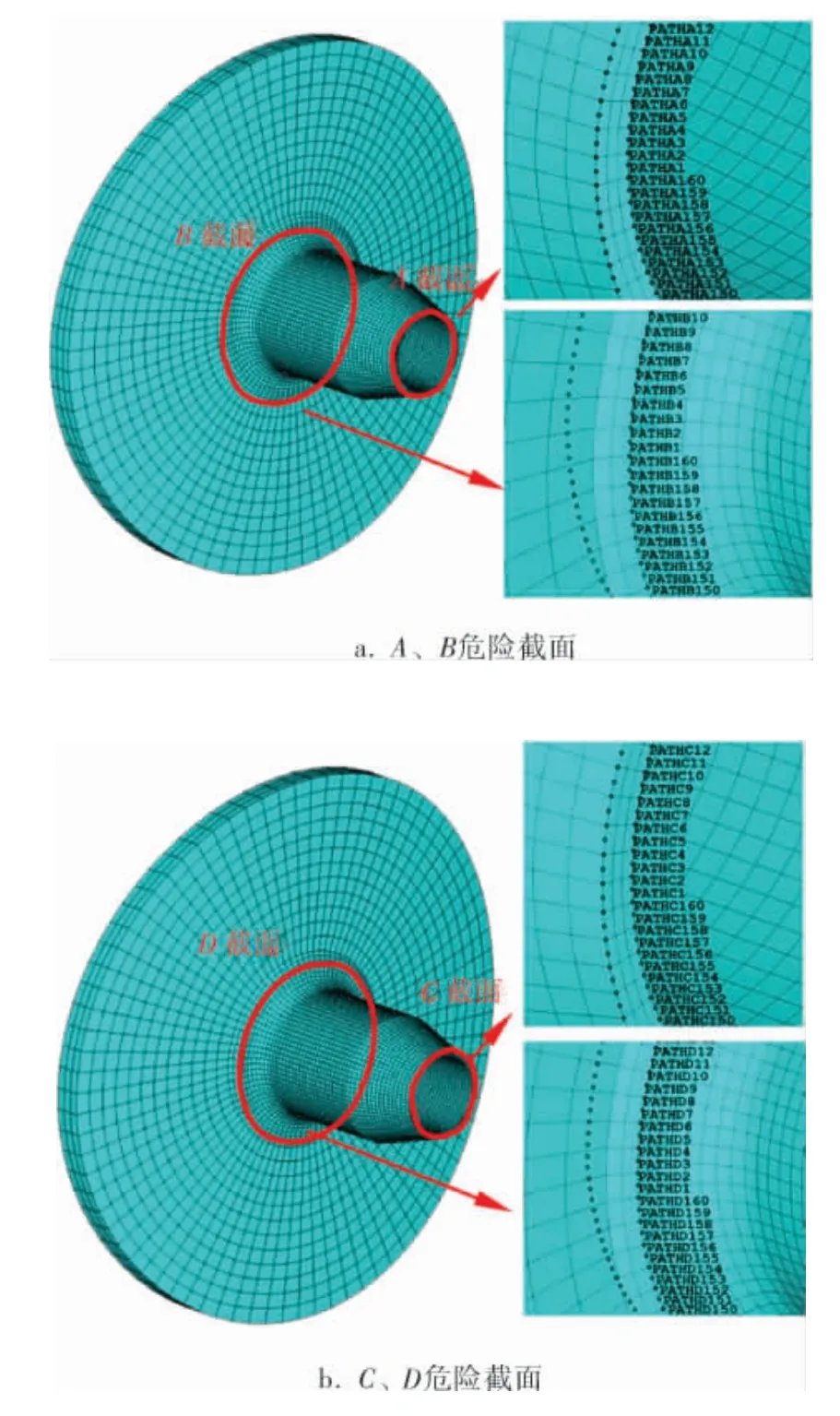
圖2 不同危險截面路徑示意圖

2.3 建立數據庫

2.3.1 接管載荷應力結果數據

在兩個容器接管處分別施加3個方向的單位力和3個方向的單位力矩，本算例中的單位力取1 kN，單位力矩取1 kN·m。 其中x方向沿著容器接管向外，z方向沿著容器管口豎直向上，y方向由右手螺旋定則確定。 Fx1、Fy1、Fz1、Mx1、My1、Mz1為施加在1號接管上的3個方向上的力和力矩；Fx2、Fy2、Fz2、Mx2、My2、Mz2為施加在2號接管上的3個方向上的力和力矩。 輸出每個載荷、每個危險截面上和每條路徑的計算結果［11］。 兩接管結構參數一致，故C、D截面的應力結果與A、B截面的應力結果具有一致性，由于篇幅所限，僅列出有代表性的A、B、E3個截面所有路徑下的應力結果。 由于采用ASME規范的第Ⅲ卷，ND篇和NF篇評定， 故輸出應力結果為最大主應力和最小主應力絕對值的最大值；1號接管上的接管載荷， 在2號接管的局部區產生的應力較小， 均小于0.01 MPa。 反之亦然，說明此容器兩個接管的載荷對彼此的局部區相互影響較小，故其結果不在圖中展示，應力結果如圖3～5所示。

對比分析圖3、4可知，在接管局部區的A、B截面上，單位力和單位力矩產生的應力結果具有一定的對稱性，這與結構的對稱性保持一致；單位力矩載荷產生的應力值要比單位力載荷產生的應力值大，即接管載荷的力矩對應力計算結果的影響較大。

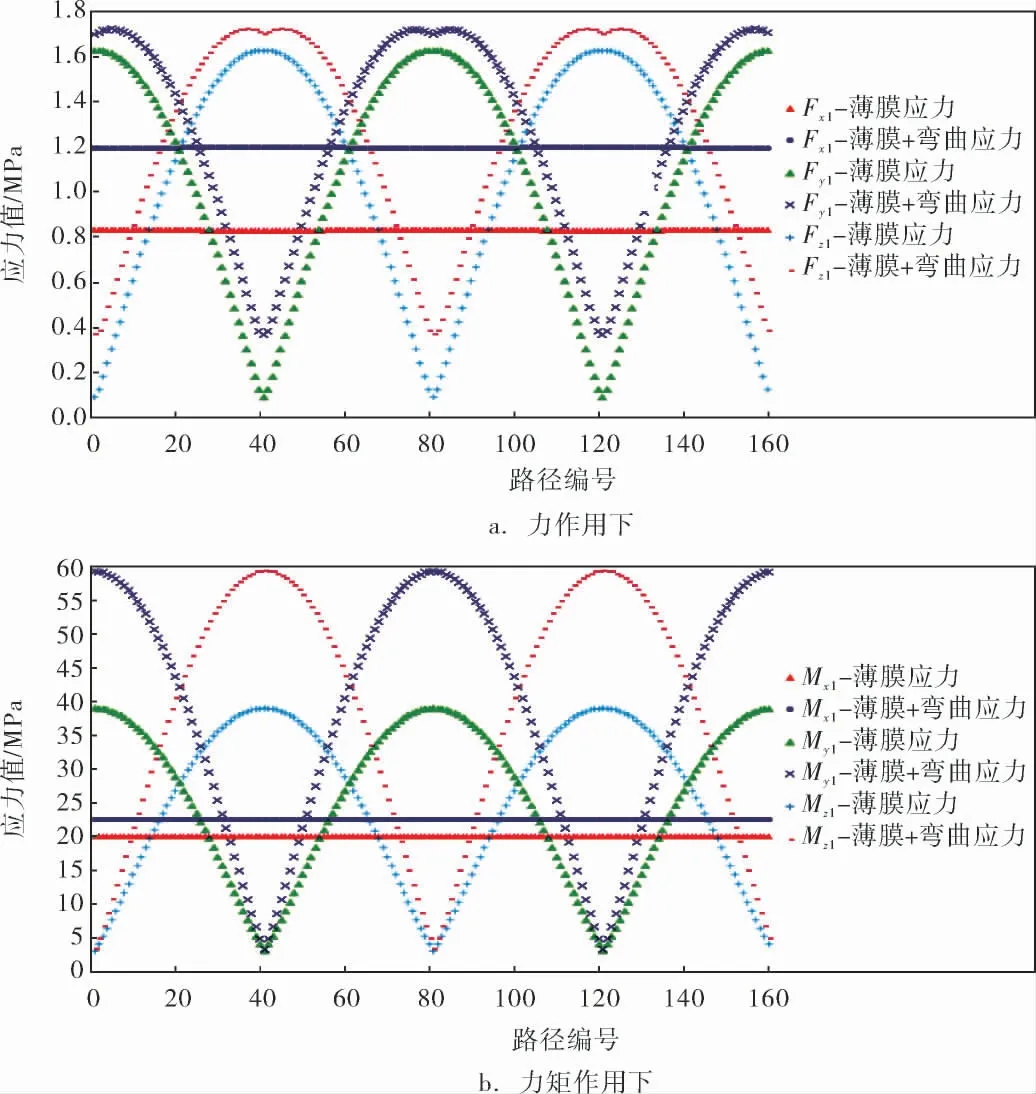
圖3 接管載荷作用下A截面路徑應力結果

圖4 接管載荷作用下B截面路徑應力結果

對比分析圖5可知， 在接管局部區的E截面上，單位力和單位力矩產生的應力結果具有一定的對稱性，這與結構的對稱性保持一致；由于接管的具體位置對單位力產生的應力值有影響，接管力和接管位置共同影響支撐件的評定結果，故容器支撐件的應力水平也將制約容器的許用接管載荷。

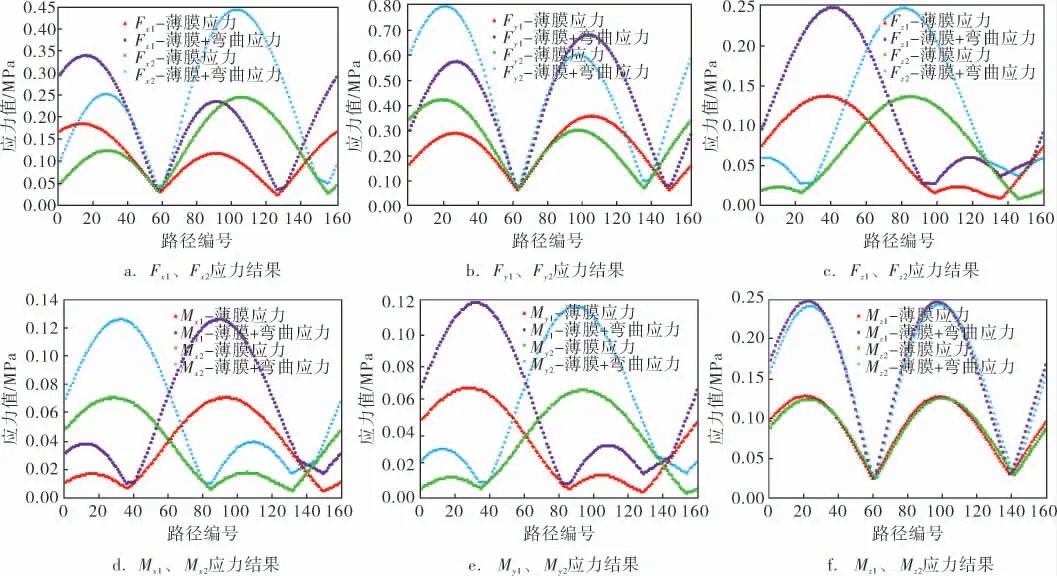
圖5 接管載荷作用下E截面路徑應力結果

2.3.2 壓力載荷應力結果數據

在容器內壁施加單位壓力，本算例中單位壓力取1 MPa。 輸出單位壓力載荷，在每個危險界面上每條路徑的計算結果。 由于篇幅所限，僅列出有代表性的A、B、E危險截面上所有路徑的應力結果，此應力結果為最大主應力和最小主應力絕對值的最大值，如圖6所示。

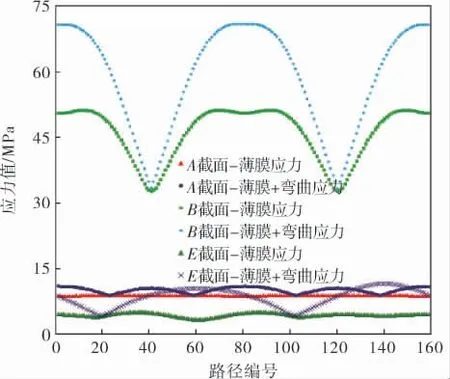
圖6 壓力載荷在A、B、E截面路徑應力結果

分析圖6可知， 在接管局部區的A、B、E截面上，單位力和單位力矩產生的應力結果具有一定的對稱性，這與結構的對稱性保持一致；壓力在B截面上產生的應力較大， 故壓力項在B截面上對最終的應力評價結果影響較大。

2.4 建立簡化計算表格

根據1.4節的方法創建簡化計算表，其中應力限值按照選取規范的要求制定， 本算例選用ASME規范［8］，表1根據規范要求列出承壓件和支撐件在設計和A級使用限制的應力限制； 焊縫為全焊透焊縫，其強度與母材相同，此算例無需特殊評定。 計算表需要實現快速調用數據庫中的應力結果，高效完成接管載荷校核，并可以根據計算結果和應力限值換算每個容器接管的最大接管載荷，綜合考慮接管局部、承壓結構區域、支撐件及焊縫處等的計算結果［12，13］，最終輸出該容器在指定載荷比例下的一組接管許用載荷。

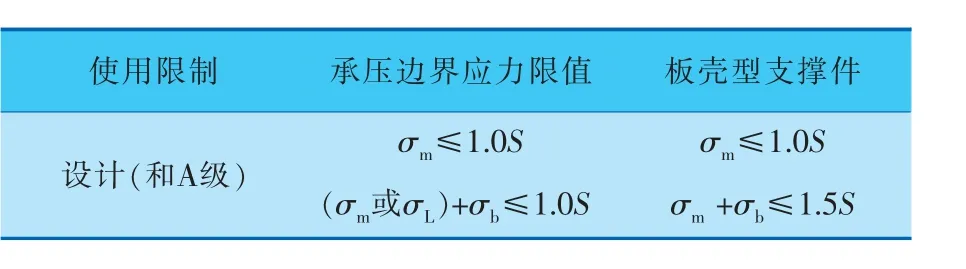
表1 設計和使用載荷應力限制

3 簡化計算方法保守性論證

建立簡化計算表后，可以快速計算指定載荷比例下的一組容器的接管載荷，為了論證簡化計算方法的保守性，采用上節所列算例，內壓載荷定為1.5 MPa， 假定接管載荷的3個力大小相同，3個力矩大小相同， 并假定力矩與力的比值為k，k取0.3～3.0，步長取0.3，列出每個k值下采用簡化計算方法得到的接管許用載荷，由于本算例中兩個接管局部區設計參數一致，且接管載荷對容器支撐件、焊縫處影響較小，在載荷間比例關系相同的情況下，兩個接管許用載荷相同，如圖7所示。

圖7 接管許用載荷圖

根據不同k值下的接管許用載荷，針對3類危險截面A、B、E， 將簡化計算方法的結果和有限元方法的結果進行對比，結果如圖8所示。

圖8 各截面應力結果對比圖

結合10組接管許用載荷計算結果，在相同模型、相同載荷的作用下，簡化計算方法得到的應力比均大于有限元方法計算得到的應力比。 通過與有限元方法結果數據對比，簡化計算方法得到的結果，A截面平均安全余量為23.89%，B截面平均安全余量為6.97%，E 截面平均安全余量為8.26%。 產生安全余量的原因是簡化計算方法采用應力結果當量疊加，使得最終的計算結果不可避免地存在一定的保守性，最終反向換算的容器接管載荷值，也具有一定的保守性；其中A截面安全余量較大，其原因是在接管的局部區存在結構的局部補強，路徑的選取位置為局部區，計算的應力結果存在二次應力的影響。 有限元詳細計算方法采用應力場矢量疊加，相對更精確。

由上述結論可知，計算結果與理論分析具有一致性，簡化計算方法具有一定的保守性。

4 結束語

筆者通過選取容器危險截面，建立應力結果數據庫，創建簡化計算表，得到一種針對已設計固化容器接管許用載荷的計算方法。 該方法可根據實際接管載荷的比例關系和容器內壓載荷大小，高效快速地計算容器許用接管載荷，為解決工程中該類問題提供借鑒。 結合有限元計算方法，通過算例對比分析，論證了該方法的保守性。