基于應力-時間雙閾值條件的巖石黏彈塑性蠕變模型
崔阿能,胡 斌,2,崔 凱,劉 楊,李 京
(1. 武漢科技大學 資源與環境工程學院,湖北 武漢 430081;2. 冶金礦產資源高效利用與造塊湖北省重點實驗室,湖北 武漢 430081)
0 引言
巖體工程的長期穩定性受巖石蠕變特性影響[1-2],常因在外荷載長期作用下導致巖石失穩,引發工程事故,然而巖體工程失穩破壞必然經歷加速蠕變階段[3-4],經典的流變模型只能描述巖石的穩態蠕變[5],建立能夠描述巖石蠕變過程中非線性特征的蠕變模型是研究的熱點和難點。目前,國內外的學者們對于巖石的非線性流變本構模型已取得了一些研究成果。
自1869年麥克斯韋提出材料是黏彈性的,便開啟了流變學的研究。1939年Griggs[6]首次對灰巖、頁巖和砂巖等巖石進行了蠕變試驗研究,指出當應力水平為破壞荷載的12.5%~80%時,巖石具有明顯的流變特性。在國內,陳宗基、孫鈞等學者首先開始對巖體流變學進行系統性的研究。徐衛亞等[7]建立了能充分反映巖石加速流變非線性特性的河海模型。蔣樹等[8]將非線性流變模型進行二次開發應用,實現了邊坡漸進性失穩破壞的數值模擬研究。劉文博等[9]結合最小耗能原理提出了一種考慮巖石損傷的蠕變模型。曹平等[10]在研究節理巖體蠕變曲線時,引入了一種應變觸發元件描述加速蠕變破壞階段的非線性特征。徐平等[11]采用柔性板法進行了巖體蠕變試驗研究,得到了相應的蠕變模型及模型參數,為工程設計提供了參考依據。韓陽等[12]基于損傷力學理論對Burgers模型進行了改進,改進后的模型能很好地描述加速蠕變階段的非線性特征。
HU Bo等[13]進行了硬巖蠕變試驗,研究了硬巖蠕變三階段的變形隨時間的變化關系,提出了一種含分數階導數阻尼器的非線性黏彈塑性模型。Ningyu Zhao等[14]利用TFD-2000巖石三軸流變試驗系統進行蠕變試驗,研究了不同應力水平條件下的巖體的時變變形規律。Marco Emanuele Discenza等[15]通過巖體蠕變試驗研究了巖體的黏塑性,表明巖體的黏性是隨加載應力和時間變化的,提出了等效黏度的概念。
針對經驗蠕變模型物理意義不甚明確,以及一些流變模型過于復雜,僅適用于某一類巖石的不足,本研究將從巖石蠕變試驗中黏滯系數隨不同應力水平和不同蠕變階段變化的角度,建立包含應力、時間以及加速蠕變啟動條件的黏性元件,結合經典蠕變模型,得到一種新的蠕變模型,包含應力閾值和時間閾值雙門檻條件,能準確表征蠕變曲線在衰減蠕變階段和加速蠕變階段非線性特征,適用性廣,模型參數易求解。
1 建立非線性黏彈塑性流變模型
1.1 巖石蠕變試驗應變-時間曲線分析
如圖1所示,完整的巖石流變曲線包含瞬時彈性變形、衰減蠕變、等速蠕變及加速蠕變4個階段,是彈性、黏性、塑性、黏彈性和黏塑性等多種變形共存的一個復雜過程。
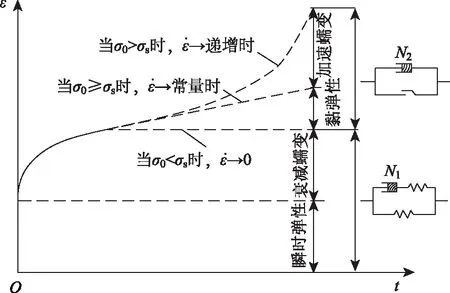
圖1 巖石蠕變試驗應變-時間曲線Fig.1 Strain time curves obtained by rock creep test
在低應力狀態下,巖樣在加載的瞬間產生瞬時彈性應變,隨后蠕變速率衰減較快,并進入穩態蠕變階段,可以用經典的流變模型飽依丁-湯姆遜體描述,但由于該模型由線性元件組合而成,對于衰減蠕變階段的非線性特征擬合度精度不高,需進一步改進。
在高應力水平作用下,巖石發生穩定蠕變后可能會發生非穩定蠕變變形。目前,主要采用應力閾值(長期強度)開關作為加速流變特征的觸發途徑。然而,通過對不同巖性的巖石在不同應力水平下的蠕變曲線進行分析,當加載應力接近或者大于長期強度時,巖石發生黏塑性破壞類型不同,從穩定蠕變階段進入非穩定蠕變階段的起始時間及持續時間不同,相應的應變-時間曲線在加速蠕變啟動時刻表現為偏塑性突變型和偏黏塑性圓滑型,理論上當蠕變速率不為0時巖樣最終會進入加速蠕變階段發生黏塑性破壞,只是流變歷時不同而己,因此以某個應力閾值作為加速蠕變啟動條件難以準確描述進入加速階段的時間和持續時間。
1.2 模型建立
1.2.1 初始瞬時彈性變形和衰減蠕變階段
孫鈞等[16]通過對大量的巖石流變試驗曲線進行分析,得到在低應力水平下,巖石發生初始瞬時彈性變形后進入減速蠕變階段,黏性系數隨著加載應力的增大而減小,隨著時間的增加而增加,此階段的黏性系數符合關于應力和時間的復合冪函數關系,建立新的黏性元件N1,滿足如下關系式:
(1)
式中,σv,tv為標準參考應力和參考時間,取值為1;n為與應力水平相關的流變指數。
將N1替換飽依丁-湯姆遜體中的牛頓黏壺,則有:
(2)
對于胡克體:
(3)
改進后的飽依丁-湯姆遜體本構方程為:
(4)
在恒定應力σ0作用下,解上述微分方程,得到改進后的飽依丁-湯姆遜體蠕變方程:
(5)
當t=0時,黏性體相當于剛性體,并未產生瞬時應變:
(6)
將式(6)代入式(5)得:
(7)
1.2.2 等速蠕變及加速蠕變階段
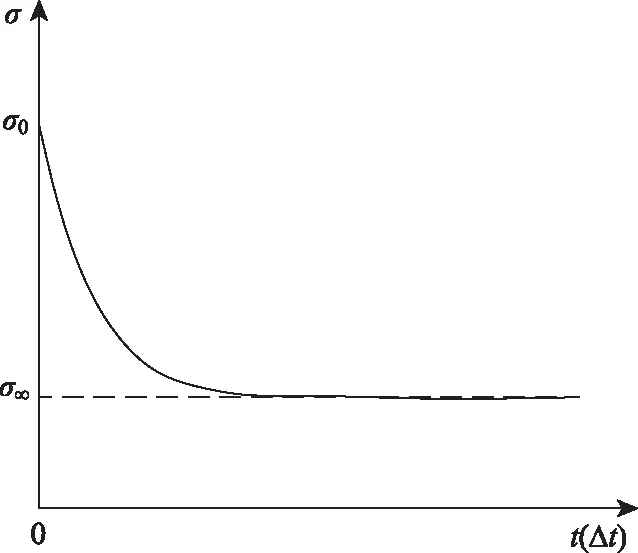
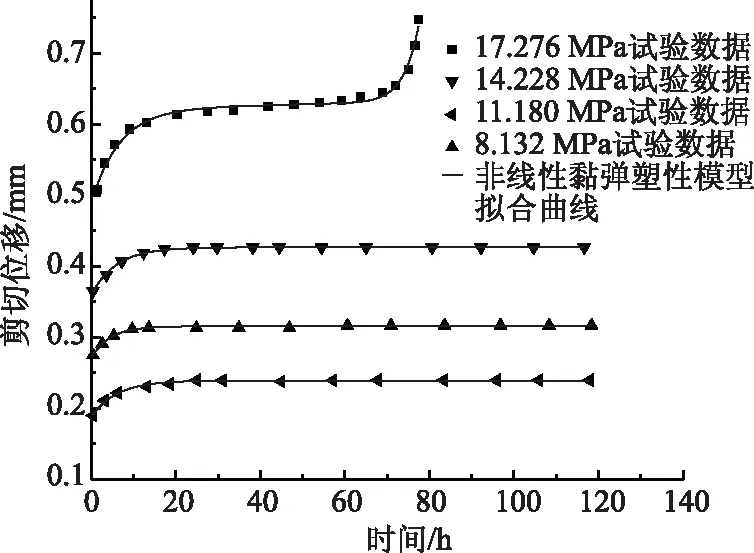
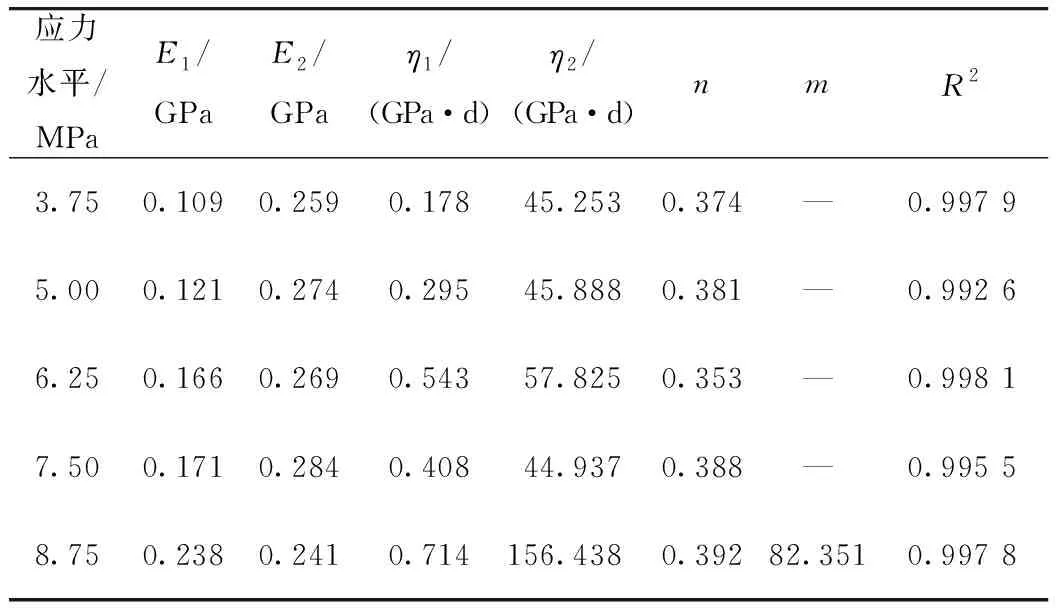
當σ0≥σs時,不同巖性的巖石在不同應力水平條件下進入加速蠕變階段的時間不同,但只要時間足夠長,終將進入加速蠕變階段,此階段的黏性系數隨著應力和時間的增加而減小[16],符合關于應力和時間的復合指數函數關系。同時引入加速蠕變時間閾值開關t*,當t (8) 式中,m為與巖石巖性相關的材料參數。將N2與塑性元件并聯組成新的非線性黏塑性元件,其本構方程為: (9) 當σ0≥σs時,解上述微分方程,得改進后的非線性黏塑性元件蠕變方程為: (10) 1.2.3 一維非線性黏彈塑性流變模型 如圖2所示,首先建立非線性部分的微分方程,然后通過積分得出該部分的蠕變方程,再通過疊加法得到新的非線性黏彈塑性流變模型的蠕變方程[17]。 圖2 一維非線性黏彈塑性蠕變模型Fig.2 One-dimensional nonlinear viscoelastoplastic creep model 一維蠕變方程為: (11) 定性分析非線性黏彈塑性流變模型的穩定性,令: (12) 式(5)簡化為: (13) 對式(14)求解關于時間變量的一階導數和二階導數,得: (14) (15) 由于A,B,C均大于0,則式(14)恒大于0,式(15)恒小于0,即式(5)為隨時間遞增的凸函數,可以描述衰減蠕變階段變形值遞增、蠕變速率遞減的特征。 同理對式(10)關于時間的一階導數和二階導數進行分析,得:當t 如圖3、圖4所示,模型參數n主要影響衰減蠕變階段的蠕變速率,取值范圍為0 圖3 低應力水平下的巖石蠕變曲線Fig.3 Creep curves of rock at low stress level 圖4 高應力水平下的巖石蠕變曲線Fig.4 Creep curves of rock at high stress level (1)E1,E2,η1,n的確定 當t=0時,對于初始瞬時彈性變形值和減速蠕變階段: (16) 當t→∞時: (17) 聯立式(16)、式(17),得到E1,E2,再通過衰減蠕變階段的試驗值時即可求得n,η1。 (2)η2的確定 當σ0≥σs且t (18) 結合牛頓黏性體的蠕變方程得: (19) 當σ0≥σs且t≥t*時,根據上述方法,采用分段擬合的形式,確定E1,E2,n,η1,η2,然后代入式(11),根據加速蠕變階段試驗值即可求得模型參數m。 上述模型參數均可在Origin軟件中通過建立自定義函數,采用最小二乘法,根據試驗得到的x組(ti,εi)試驗值,進行非線性擬合確定。 不同巖性的巖石具有不同的蠕變特性,例如軟巖在應力水平接近長期強度值時,以幾乎恒定的蠕變速率產生蠕變變形,而硬巖在穩態蠕變階段應變基本不發生變化。為準確描述巖石蠕變破壞的非線性特征,確定加速蠕變階段的起始時間尤為重要,且加速蠕變啟動時間的選擇會影響到各流變力學參數的計算結果。 (1)根據蠕變速率突變點確定 當應力水平大于加速蠕變應力閾值時,巖石由穩態蠕變階段進入加速蠕變階段,加速蠕變啟動時間可以根據蠕變速率-時間曲線的突變點直接確定。例如文獻[18]中巖石在8.78 MPa應力水平作用下,第15 h時,蠕變速率突然增大到1.68×10-3/h,且呈加速持續增長的趨勢。因此,判定在該級應力水平作用下加速蠕變啟動時間t*=15 h。 (2)巖石蠕變破壞時間與應力水平的關系 一些學者[16,19]在研究巖石長期強度值時,通過對一定數量的巖石蠕變試驗結果進行研究,發現快剪、快壓試驗得到的瞬時強度值最高,破壞荷載隨流變時間(t)及加速流變歷時(Δt)的增加呈減小的趨勢,符合指數函數關系,如圖5所示: (20) (21) 圖5 破壞荷載與蠕變歷時的關系Fig.5 Relationship between failure load and creep duration 聯立式(20)、式(21)得加速蠕變破壞的起始時間為: (22) 式(22)為巖石發生蠕變破壞的時間與應力水平的一般關系式,根據巖石蠕變試驗擬合得到參數α,β值,通過式(24)可以推算出不同應力水平下巖石蠕變破壞的起始時間及流變歷時,對于巖體工程穩定性預警、預測研究意義重大。 實際巖體工程中巖石處于三向應力狀態,對于三維應力狀態下的彈性體,材料內部任一點的應力張量σij可以分為球應力張量σm和偏應力張量Sij;應變張量εij分為球應變張量εm和偏應變張量eij,由: 根據教學大綱,選用人衛出版社《影像診斷學》第4版骨肌肉系統章節中的骨折、骨關節感染(化膿性骨髓炎、化膿性關節炎、骨關節結核)、骨腫瘤、骨腫瘤樣病變和代謝性骨病四個章節作為教學內容,各組進行12學時的翻轉課堂教學。兩組教學大綱、教材、教學進度以及課時數均相同,且由同一位教師授課。 (23) 可得: σij=Sij+δijσm, (24) 式中δij為克羅內克函數: (25) 同理得到: εij=eij+δijεm。 (26) 對于常規三軸壓縮蠕變試驗: (27) 結合式(24)、(27)得: (28) 對于三維應力狀態下的胡克體: (29) 式中,K為體積模量;G為剪切模量。結合一維蠕變方程,根據文獻[20]采用類比法,得到彈性體三維蠕變方程: (30) 黏性體的三維蠕變方程為: (31) (1)當σ0<σs時: (32) (2)當σ0≥σs且t (33) (3)當σ0≥σs且t≥t*時: (34) (35) 式中F0為屈服函數初始值,一般取1[21]。 由于Mohr-Coulomb屈服準則不能考慮中間主應力對巖石屈服的影響,Von-Mises屈服準則忽視了球應力對巖石蠕變特性的影響,筆者采用 Drucker-Prager屈服準則,其表達式為: (36) 式中,J2為應力偏量第二不變量: (37) 筆者采用文獻[18]及文獻[22]中流變試驗數據對上述建立的非線性黏彈塑性蠕變模型的適用性及正確性進行驗證。 文獻[18]為現場大尺寸壓縮流變試驗,試樣為節理裂隙較為發育的微風化砂巖,試樣尺寸為730 mm×730 mm×780 mm,采用逐級加載方式。根據試驗結果,在應力水平為8.78 MPa時,取t*=15 h,σ∞=7.50 MPa。 文獻[22]為室內小尺寸剪切流變試驗,試樣為塊狀構造斑狀結構的灰白色花崗巖圓柱體,尺寸為50 mm×100 mm,采用逐級加載方式。根據試驗結果,在應力水平為17.27 MPa時,t*=70 h,σ∞=15.57 MPa。 結果如圖6、圖7、表1、表2所示,擬合效果很好,在最高級應力水平作用下,文獻[18]和文獻[22]的蠕變曲線擬合度分別達到了0.997 8和0.978 4,這說明基于巖石蠕變試驗中黏性系數在不同應力水平和不同蠕變階段中的變化規律建立的巖石非線性黏彈塑性蠕變模型,能反映巖石蠕變全過程曲線特征,解決了傳統流變模型在衰減蠕變階段擬合精度不高、無法描述加速蠕變階段非線性特征及適用性不高的缺陷,且流變破壞物理意義明確。 圖6 軟弱巖體現場試驗:不同應力水平下的蠕變曲線Fig.6 Field test of soft rock mass: creep curves at different stress levels 圖7 飽水花崗巖室內試驗:不同應力水平下的蠕變曲線Fig.7 Laboratory test of saturated granite: creep curves at different stress levels 表1 軟弱巖體現場壓縮蠕變試驗模型擬合參數值Tab.1 Fitting parameters of in-situ compression creep test model of soft rock mass 表2 飽水花崗巖室內剪切蠕變試驗模型擬合參數值Tab.2 Fitting parameters of indoor shear creep test model of saturated granite (1)基于巖石蠕變試驗中黏性系數在不同應力水平和不同蠕變階段中的變化規律建立了參數求解簡單、流變破壞物理意義明確的五元件非線性黏彈塑性蠕變模型。 (2)通過模型穩定性和參數敏感性分析,并結合現場大尺寸軟巖壓縮流變試驗和室內小尺寸飽水花崗巖剪切流變試驗,從理論和試驗兩方面驗證了所建模型的正確性與適用性。 (3)當應力水平接近或者大于巖體的長期強度時,巖石并不會立即進入加速蠕變階段發生黏塑性破壞,采用應力閾值和時間閾值雙開關能精確刻畫巖石加速蠕變階段的非線性特征,對于巖體工程中因巖石流變特性失穩預測方面的研究具有重大意義。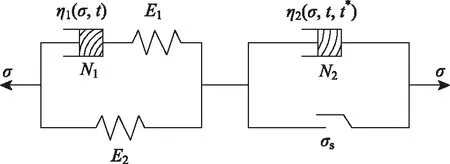
2 理論驗證
2.1 非線性黏彈塑性流變模型的穩定性分析
2.2 模型參數的敏感性分析
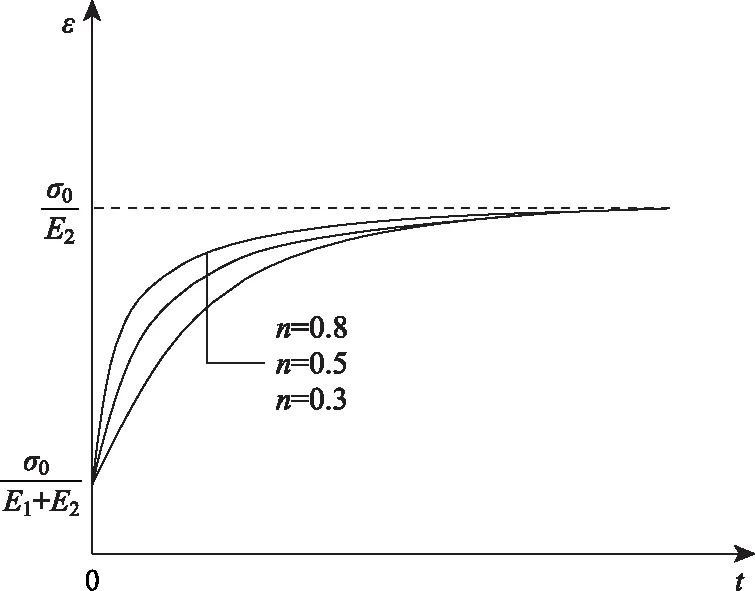
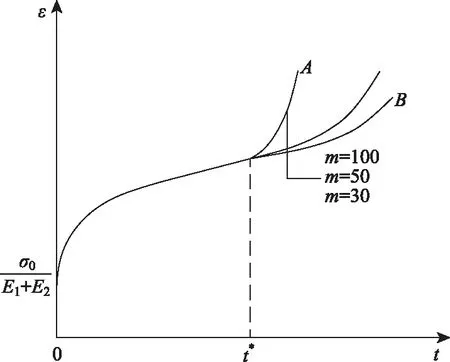
3 模型參數辨識
4 加速蠕變啟動條件
5 三維蠕變方程
6 試驗驗證


7 結論

