基于熱聲解耦方法的燃燒不穩定性預測

高宇鵬，李俊杰 ，劉巍，李敬軒

1.北京動力機械研究所，北京 100074 2.北京航空航天大學 宇航學院，北京 100191

0 引 言

燃燒不穩定現象廣泛存在于火箭發動機、航空發動機以及大型空氣加熱器等裝置中，會使燃燒器內產生不可控的巨大壓力脈動，造成發動機回火、熄火，燃燒器壁面過熱，導致發動機壽命縮短甚至損毀等一系列問題。20世紀60年代，在對F-1火箭發動機初始方案的44次試車中，超過半數的試車都發生了燃燒不穩定現象；其振幅甚至達到了燃燒室平均壓力的100%。因此，為盡可能減少不穩定燃燒帶來的巨大危害，通常采用實驗和數值仿真等方法對燃燒不穩定性機理進行研究。

王迪等對單噴嘴模型發動機進行了實驗研究，測量了不同燃燒室和噴嘴縮進長度對燃燒穩定性的影響，結果發現增加縮進長度會對縱向高頻燃燒不穩定性產生阻尼作用，燃燒室長度對縱向高頻燃燒不穩定性的影響比縮進長度更為明顯。Richecoeur等對液氧/氣態甲烷多噴嘴模型燃燒室進行了試驗研究，結果發現橫向壓力震蕩與燃燒和火焰之間存在強烈的耦合作用，可增大火焰膨脹率以及火焰向壁面的傳熱率。Bibik等拍攝了燃燒室內部氣流的旋轉過程，發現氣流旋轉方向與中心噴嘴旋轉相同，認為中心噴嘴是激發切向不穩定的重要因素。Méry等實驗研究了液氧/甲烷燃燒室在存在擾動的條件下，聲學擾動與火焰之間的相互作用。結果表明：在中等擾動條件下，液體射流存在橫向周期性振蕩；大幅度擾動時，火焰隨聲學擾動而周期性振蕩。Sliphorst等通過實驗研究發現，燃燒不穩定激勵主要來自于火焰與聲學振蕩的耦合作用。

Urbano等通過大渦模擬（Large Eddy Simulation, LES）對功率為80 MW的全尺寸燃燒器進行仿真，結果發現一階切向和一階縱向不穩定對燃燒室的不穩定性起重要作用，并且與混合燃料的噴注過程強烈耦合。Shimizu等等對液體火箭發動機（Liquid Rocket Engine, LRE）進行了切向數值仿真，認為平均流動分布控制一階切向不穩定的發生。Staffelbach等對自激振蕩的環形燃燒室進行了大渦模擬，成功捕捉了燃燒室自激振蕩頻率，發現其特征是由兩種不同振幅的旋轉模式疊加而成。王方、張志浩和夏朝陽等均采用LES對發動機內燃燒不穩定性進行詳細的研究。Li等對ORACLESL長火焰燃燒室進行了預測。采用大渦模擬獲得系統的火焰傳遞函數，并將此傳遞函數帶入到Li和Morgans等開發的燃燒不穩定預測和模擬程序—OSCILOS中，最終得到了精準的熱–聲振蕩頻率和幅值的預測值。

綜上所述，前人已通過實驗和數值的方法對熱聲耦合不穩定燃燒進行了研究，但是大尺寸燃燒器燃燒不穩定性的預測一直存在計算量太大的問題。本文將通過熱–聲解耦的方法，對某型空氣加熱器燃燒不穩定性進行預測，為加熱器熱試提供技術支撐。

1 燃燒-聲學解耦方法

本文基于Li等的方法，將燃燒對擾動的響應計算與聲學計算解耦，即分別計算火焰對聲學擾動的響應（通常表征為火焰傳遞函數）和聲學系統在熱源擾動下的響應。因此，對于燃燒的數值模擬只需考慮燃燒室內的火焰對來流擾動的響應，不需要考慮包括集氣環和噴管在內的整個發動機系統，顯著降低了計算量，提高了計算速度。

1.1 噴管聲學邊界條件計算

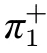
在聲學邊界條件計算中，除了噴管外，都可處理為壅塞或聲學閉口。由于噴管復雜的頻率特性，需要考慮其聲學邊界條件隨頻率的變化，通常表征為傳遞函數的形式。一般拉瓦爾噴管的聲學系統可以表示成如圖1所示模型。當噴管上游來流的物性參數發生擾動時，下游氣流會產生壓力與速度的振蕩，產

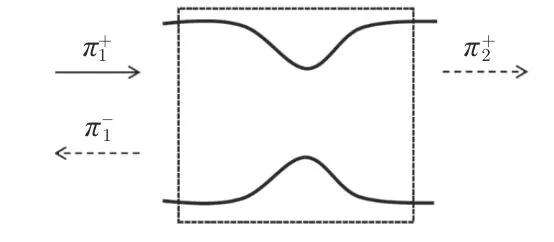
圖1 噴管的聲學模型Fig.1 The acoustic model of nozzle

對于亞聲速流噴管（圖1），將向下游傳播的聲波施加在入口處，向上游傳播的聲波施加在出口處。假設噴管中的氣體是理想氣體，建立一維線性化歐拉方程如下：

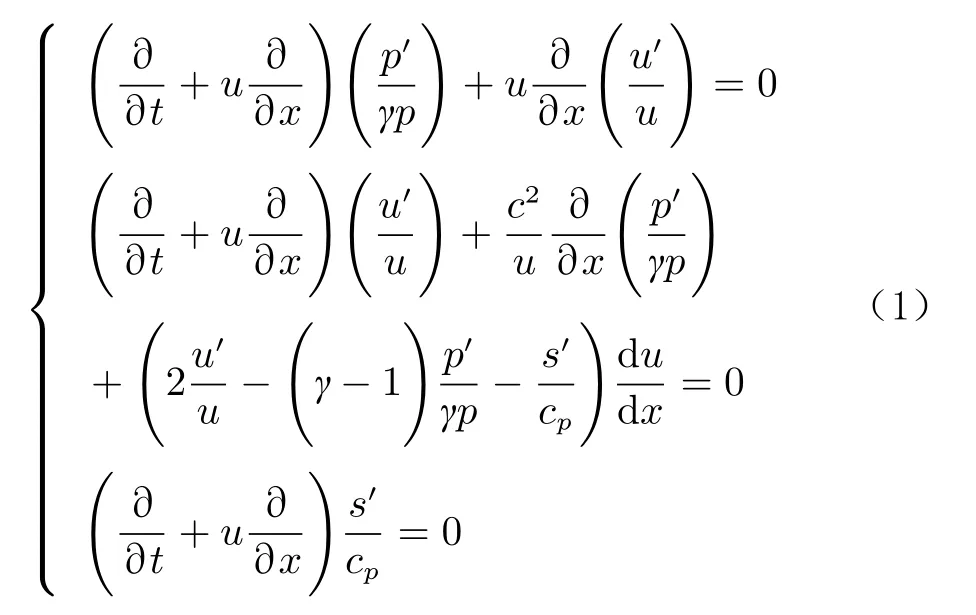
式中，u為氣體速度，p為氣體壓力，為比熱比，s為氣體熵，為 氣體定壓比熱容，為當地聲速，上標“”為擾動量。

將上述控制方程進行無量綱化處理，當馬赫數不為1時，進行傅里葉變換可以得到：

式中，=/L，為 噴管長度，x為距噴管入口的軸向距離；矩陣是由不變量構成的矢量。矩陣和的形式分別如下：

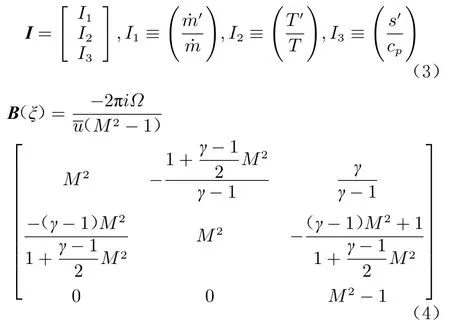
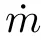
利用Magnus展開法可以求得式（2）的解，并求得最終的聲學反射系數。

1.2 數值計算方法

1.2.1 燃燒室三維建模

加熱器整體模型如圖2所示，包含噴注面板、燃燒室、噴管等部件。其中，噴注面板上包含48個燃料噴嘴和36個冷卻空氣噴嘴。燃燒室直徑為350 mm，長度為800 mm。在對比了考慮和不考慮集氣環的燃燒室聲學特性后，發現集氣環對燃燒室不穩定模態的穩定性影響基本可以忽略。且由于各種連接件的壅塞特性，因此，在燃燒不穩定性計算中忽略了集氣環這一部件。同時，由于噴注面板上噴嘴分布的高度對稱性，將采用1/6模型進行計算，如圖3、4所示。

圖2 加熱器各部件示意圖Fig.2 Schematic diagram of the heater components

圖3 燃燒室模型示意圖Fig.3 Schematic diagram of combustion chamber model

為確保火焰相關參數計算準確，對噴注面板下游200 mm范圍內的網格進行加密，其各向尺寸小于1 mm。經驗證計算，在網格量達到265萬時，滿足網格無關性要求；瞬態計算時間步長為10s時，滿足時間無關性要求，此時全局最大Courant數小于5。

1.2.2 模型選擇和參數設置

由于燃燒室內總溫為1 743 K，總壓達8.2 MPa，當預混燃料采用乙醇/液氧時，二者均處于超臨界態。超臨界流體流出噴嘴后，其氣液界面較為模糊，密度為液態的1/3，而黏度只有液態的1/12～1/4，因此其流動行為更偏向于氣體。在數值仿真中，燃料按連續相進行處理。

圖4 燃燒室網格劃分示意圖Fig.4 Divided mesh of combustion chamber model

采用ANSYS Fluent對燃燒室內的燃燒過程進行數值仿真，其中內部湍流流動采用Realizable模型求解；燃燒采用Eddy-Disspation模型求解。該燃燒模型假定燃燒速率遠大于燃料混合速率，即燃料一經混合便完全燃燒，忽略復雜的化學反應速率，采用乙醇一步總包反應機理：

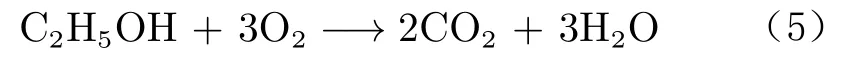
為確保在高溫高壓的燃燒室環境下，燃料物性參數（特別是對當地聲速影響極大的密度）數值準確，采用Peng-Robinson狀態方程計算。燃料入口參數如表1所示，各噴嘴入口邊界條件采用質量流量入口，燃燒室出口邊界條件則采用壓力出口。

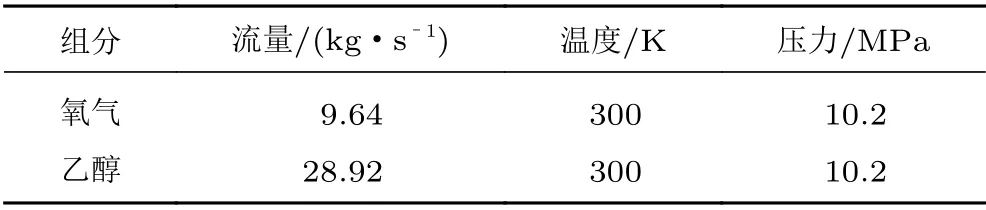
表1 預混燃料入口工況Table 1 The working conditions of premixed fuel at the inlet

得到燃燒室穩態場后，在燃料入口處施加不同頻率、振幅的正弦擾動（式（6）），即可獲得各噴嘴的熱釋放率隨時間的變化關系，進而得到各噴嘴的火焰傳遞函數：

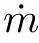
1.2.3 火焰傳遞函數的定義

通過對每個噴嘴出口的火焰熱釋放率進行處理，提取激振頻率上的擾動幅值和相位，并帶入火焰傳遞函數的定義式（式（7）），即可得到各火焰在不同頻率和不同擾動幅值下的火焰傳遞函數。

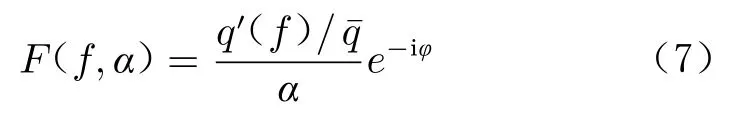
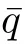
1.3 聲學模型

1.3.1 聲學模擬模型

對整個燃燒室建立Helmholtz方程并耦合火焰傳遞函數，采用噴管聲學邊界條件，即可求得整個系統的聲學模態。

對于一個有熱源的區域，流體的密度隨壓力和 熵的變化而變化，即：

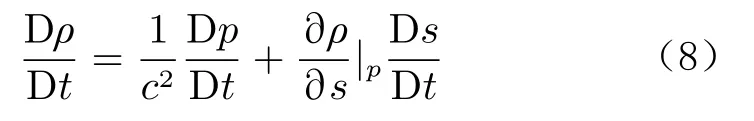
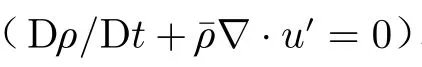
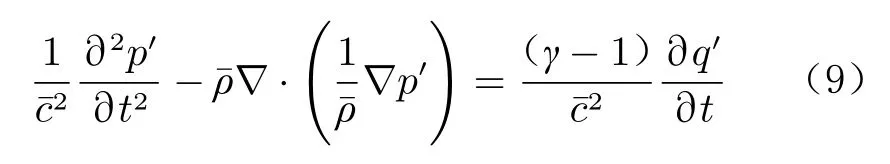
結合火焰傳遞函數的定義式（7），最終可推導得到單極域源的表達式為：

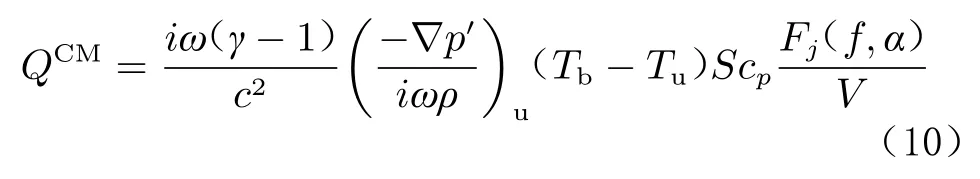
式中，下標b和u分別代表已燃氣體和未燃氣體，S為噴嘴截面積，V為熱源體積。

1.3.2 聲學邊界阻抗模型

在實際工況中，聲波在出口處存在一定的反射，即為聲阻抗R。如圖5所示，設入射波強度為A，反射波強度為A。

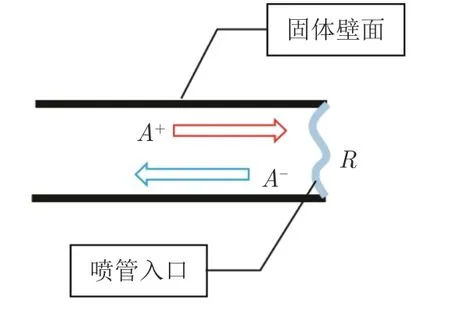
圖5 聲波反射與聲學邊界阻抗示意圖Fig.5 Schematic diagram of sound reflection and acoustic boundary impedance

當集氣環與噴注器和燃燒室解耦后，噴注器進口可認為是壓力節點，空氣燃料混合噴嘴入口可看作是硬聲場邊界，空氣噴嘴入口為軟聲場邊界。燃燒室出口與噴管相連，其聲學邊界條件采用1.1小節中推導得到的聲學反射系數模型。

聲阻抗定義為：

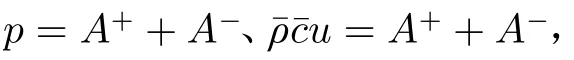
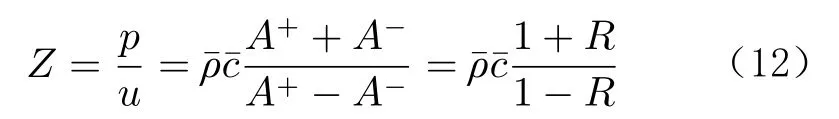
2 燃燒室不穩定模態估計

由于空氣加熱器燃燒室的噴嘴面積總和與燃燒室橫截面積之比遠遠小于1，且噴嘴內與燃燒室的溫度相差較大（約1 500 K），因此噴嘴前的聲學系統可與燃燒室內的聲學系統解耦。燃燒室出口為一壅塞的噴管，燃燒室內的聲學系統也可以與噴管下游的聲學系統解耦，故只需計算燃燒室內的聲學模態。在粗估燃燒室聲學模態的頻率時，燃燒室進口可認為是聲學閉口條件，出口由于噴管前馬赫數小于0.1,也可近似認為是聲學閉口。

燃燒室的各個聲學模態的頻率f可以根據經典公式進行粗估：

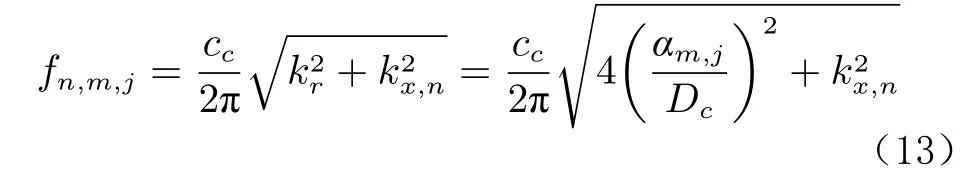
式中，、、1、、、、和分別為縱向模態數、切向模態數、徑向模態數、燃燒室聲速、徑向波數、縱向波數、垂直于縱向方向的波數和燃燒室的直徑。為 貝塞爾函數 dJ(k)/d=0的根，可通過查表2得到。

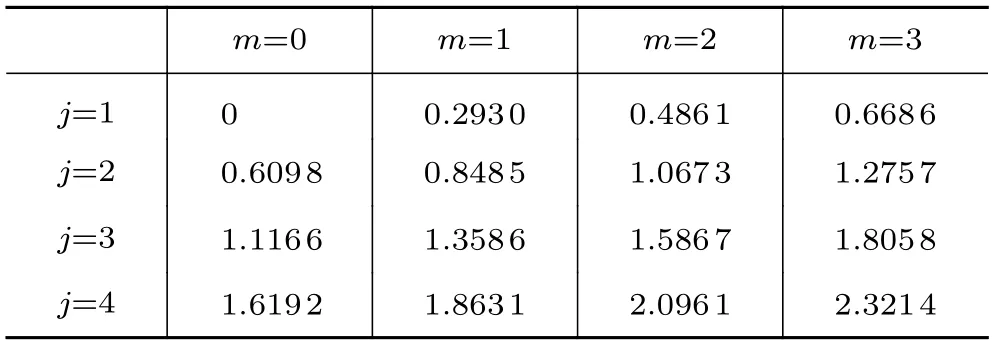
表2 不同模態下 k m,j 的值Table 2 The value of k m,j in different modes

結合加熱器燃燒室結構參數以及燃燒室內部聲速（約為837 m/s），可以粗估燃燒室的各聲學不穩定模態頻率，如表3所示。

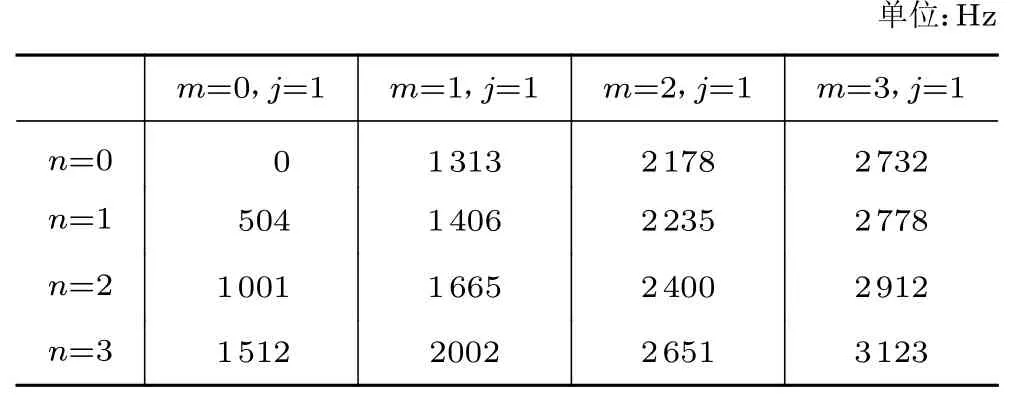
表3 燃燒室各不穩定模態頻率估計值Table 3 Estimated frequency of each unstable mode of the combustion chamber

考慮到實際加熱器燃燒室最易出現（n=1，m=1）的不穩定模態，因此最可能出現的不穩定頻率應為（n=1，m=1，j=1）模態的頻率1 406 Hz。這一粗估頻率將作為后續計算的初始參考值。

3 結果與討論

3.1 聲學反射系數計算結果

對1.1小節所得的數學方法進行求解，可得0～3 000 Hz頻率范圍內噴管聲學反射系數的幅頻、相頻特性（圖6藍色圈）。對計算結果進行五階多項式擬合，可求得噴管聲學反射系數的近似解析表達式，其頻響特性曲線如圖6中紅色實線所示。此結果可作為燃燒室聲學計算的出口邊界條件，用于計算燃燒室的各聲學模態。

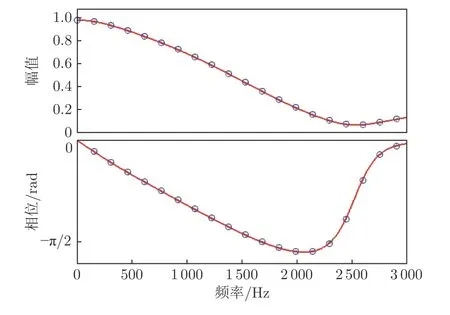
圖6 聲學反射系數的幅頻、相頻特性曲線Fig.6 Amplitude frequency and phase frequency characteristic curve of acoustic reflection coefficient

3.2 燃燒室內數值計算結果

3.2.1 溫度場分析

由于粗估燃燒室最不穩定頻率為1 406 Hz，因此取擾動頻率f =1 400 Hz、擾動振幅=04的工況進行分析。圖7為t=0.021 161 s時刻，燃燒室距噴注面板50、100、200、400 mm處截面的總溫云圖。

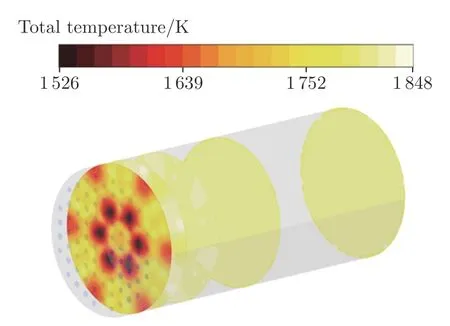
圖7 不同截面處的總溫云圖Fig.7 Total temperature contour map at different cross-sections

從圖7中可以看到，燃料噴嘴出口近場截面的溫度分布并不均勻，中心噴嘴受周圍冷卻氣流的影響更為明顯，存在明顯的低溫環（圖7中黑色區域）；隨著軸向距離的增加，冷熱空氣逐步混合，在距噴注面板約400 mm處幾乎混合均勻，燃燒室內部溫度分布趨于穩定。

3.2.2 熱釋放率分析

圖8是t=0.021 161 s、f=1 400 Hz、3種不同擾動振幅下，燃燒室中心面上的火焰熱釋放率鋒面與流線圖。其中，熱釋放率鋒面可近似認為是火焰鋒面。在施加擾動后，燃燒室的中心與邊緣靠近壁面處會分別產生兩個較為強烈的渦旋。處于中心位置的渦旋對火焰鋒面的拉伸作用明顯。在擾動振幅相對較小時，渦旋強度較低（流線相對稀疏平整），火焰鋒面平整，形狀較為舒展；隨擾動振幅增加，中心渦旋強度增加（流線更為緊湊卷曲），對火焰鋒面的影響愈發明顯，火焰產生明顯褶皺，且長度變短。邊緣渦旋對于流量脈動幅值的響應并不是很明顯。在高頻擾動下，中心渦旋造成的速度擾動直接對火焰產生擾動，造成火焰面周期性卷曲和拉伸，從而產生火焰傳播速度擾動，引起火焰熱釋放率的波動。

本文分別檢測了每一個噴嘴的熱釋放率隨時間的變化，以圖8中標注的噴嘴為例，特別對受到冷空氣擠壓的火焰進行討論。圖9（a）、（b）分別為該噴嘴在擾動振幅=04、不同擾動頻率f下和擾動頻率f1 400 Hz、不同振幅下，火焰熱釋放率隨時間變化的曲線。

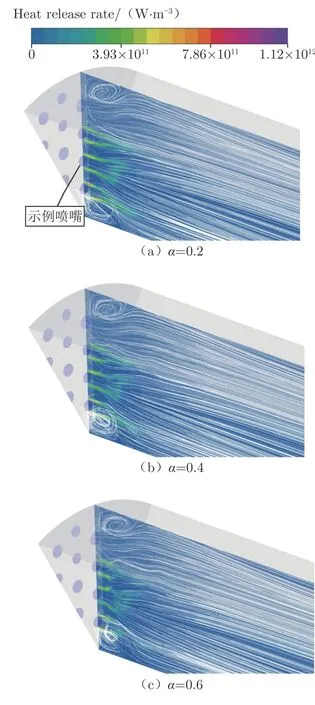
圖8 不同振幅下的燃燒室內熱釋放率云圖及流線圖Fig.8 Contour of heat release rate and streamline inside the combustion chamber under different amplitudes

從圖9（a）可以看到，當振幅相同時，該噴嘴出口火焰熱釋放率對頻率的響應不同—不同擾動頻率對應不同的熱釋放率脈動幅值。理論上，當對入口流量給定相同的擾動振幅時，擾動頻率越高，熱釋放脈動幅值應更低。但對于該噴嘴，在擾動頻率f=1 400 Hz時，其幅值相對f=1 250 Hz并未出現明顯的下降，即燃燒室內部的不穩定頻率可能出現在f=1 400 Hz附近，這一結果也證明了第2節的粗估結果是可靠的。

從圖9（b）可以看到，當擾動頻率f=1 400 Hz時，該噴嘴出口火焰對于不同振幅的響應同樣存在差異。隨擾動振幅的增加，熱釋放脈動幅值增加；但熱釋放率脈動幅值并不隨流量擾動幅值的增加而持續增加。當=06 時，熱釋放脈動幅值與=04 時并無明顯差異，這也說明了該噴嘴出口火焰對于大流量脈動的響應并不敏感。

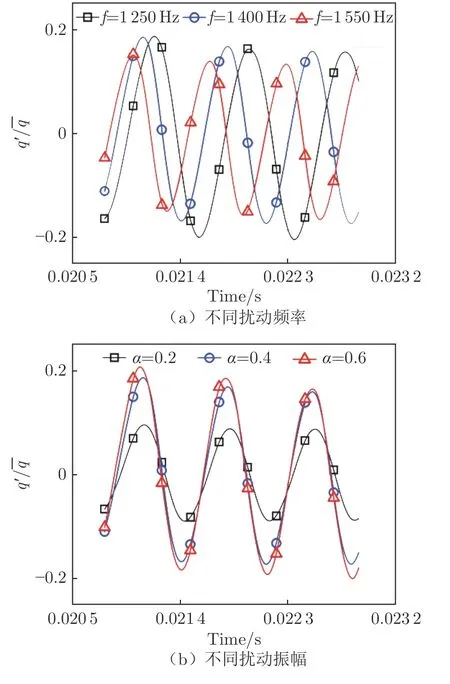
圖9 火焰熱釋放率隨時間變化曲線Fig.9 Dimensionless flame heat release rate vs.time curve

3.3 燃燒室內聲學模態預測結果

圖10為示例噴嘴（圖8）對應的火焰傳遞函數幅值和相位圖。從圖中可以看到，在任意擾動頻率和擾動振幅下，該噴嘴的火焰傳遞函數幅值均小于1，即火焰熱釋放率相對于入口流量擾動的響應呈抑制作用。并且隨著擾動流量的增加，傳遞函數幅值在各頻率下均有明顯的下降趨勢。

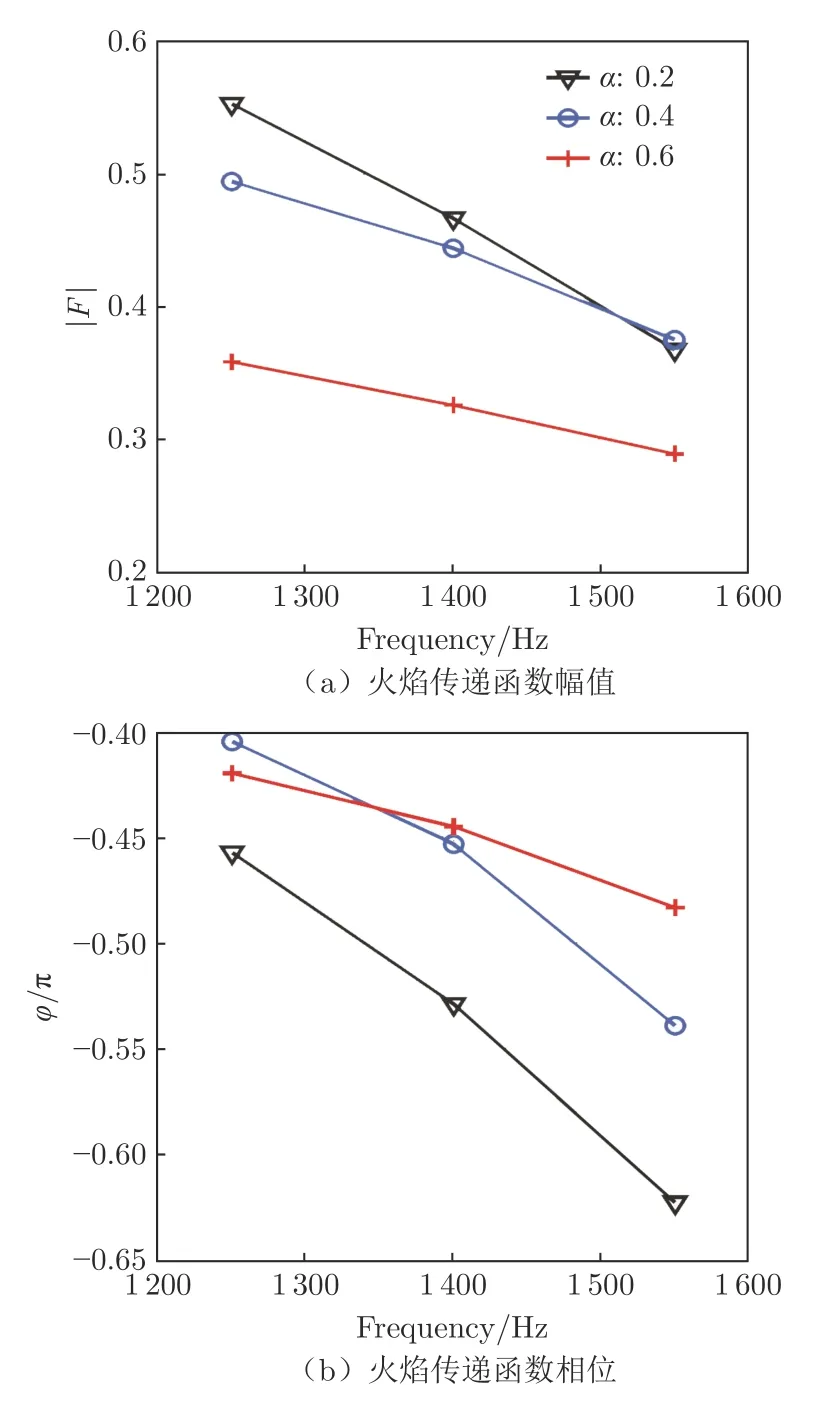
圖10 火焰傳遞函數的幅值和相位Fig.10 The amplitude and phase of the flame transfer function

將各噴嘴的火焰傳遞函數結果代入1.3小節的聲學模型中，即可對存在流量擾動的燃燒室的穩定性進行預測，預測結果如圖11所示。該圖為燃燒室無量綱（n=1，m=1，j=1）模態的壓力分布。壓力分布模式主要存在2種，分布在沿燃燒室直徑方向上互相垂直。經1.3小節中的模型計算，當擾動振幅分別為 02、04、06時，（n=1，m=1，j=1）模態的特征值分別為1 389.9+5.975 i、1 389.9+6.060 3 i和1 389.9+6.142 4 i。該特征值為復數，其實部為模態頻率，虛部為增長率。當虛部大于0時，代表燃燒室在該聲學模態上是穩定的；當虛部小于0時，代表燃燒室在該聲學模態上是不穩定的。

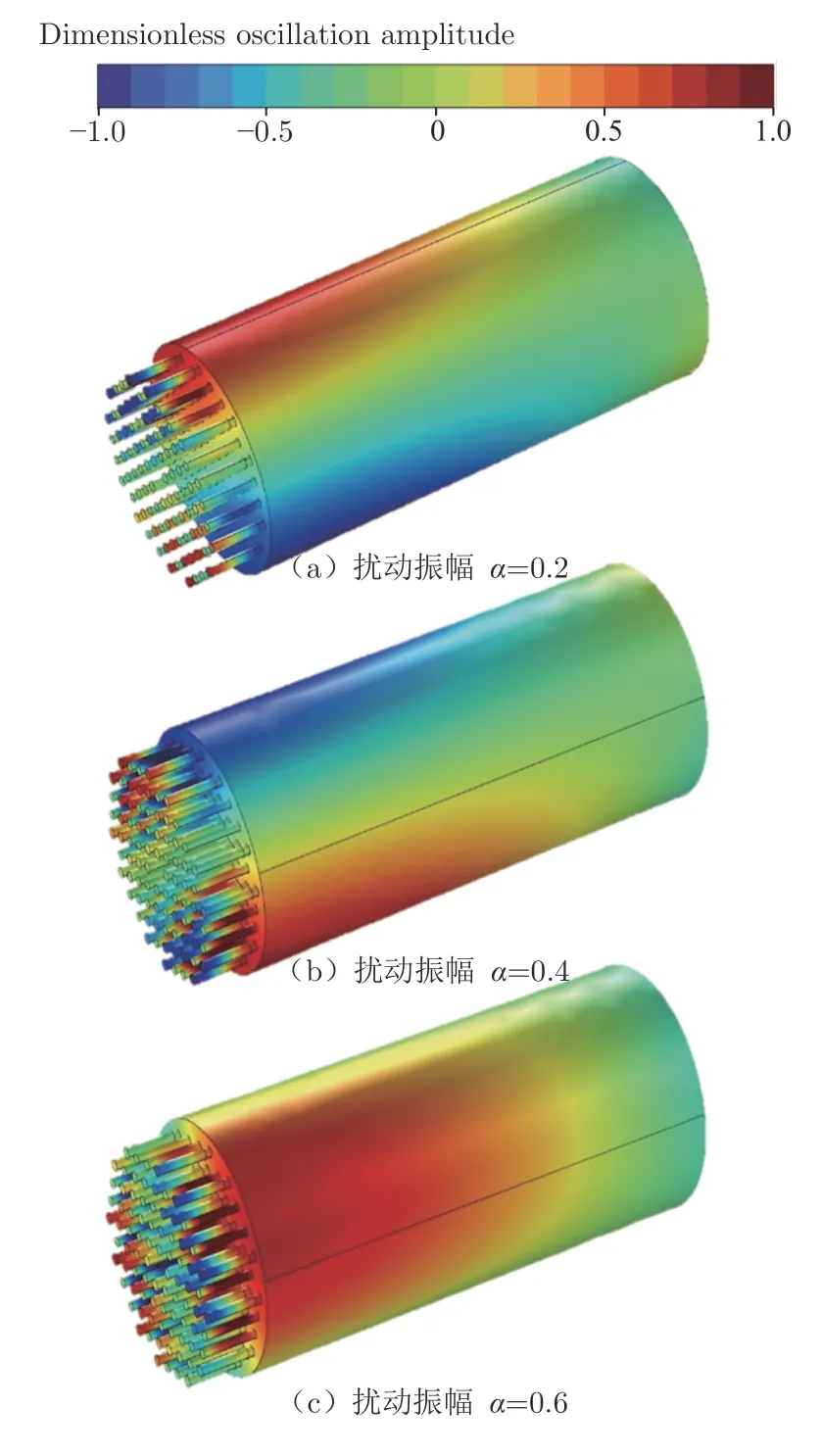
圖11 不同擾動振幅下，燃燒室最不穩定模態的總聲壓場Fig.11 The total sound pressure field of the most unstable mode in the combustion chamber

結果表明，在不同擾動幅值下，燃燒室的（n=1，m=1，j=1）模態均穩定。這與該型加熱器的試驗結果一致。該型加熱器在后期試驗中并未出現燃燒不穩定現象。另一型加熱器（燃燒室直徑為460 mm，長度為800 mm）在試驗過程中出現燃燒不穩定現象，振蕩頻率為1 100 Hz。基于第2節中的方法對該燃燒室的不穩定模態進行預測，得到振蕩頻率為1 135 Hz，與試驗測量頻率符合很好，進一步驗證了本文方法良好的預測能力。

4 結 論

1）采用Magnus展開法獲得了噴管的聲學邊界條件。通過五階多項式擬合獲得了噴管聲反射系數的近似解析表達式。

2）采用ANSYS Fluent對全尺寸燃燒器進行了非穩態數值仿真，得到了燃燒室內部存在擾動時的物理場信息，發現位于噴注面板中心處的噴嘴受到周圍冷卻空氣的影響較大。提取了每一個噴嘴的熱釋放率信息，獲得了噴嘴熱釋放率脈動與速度擾動之間的火焰傳遞函數。

3）將所得聲學邊界條件與火焰傳遞函數代入燃燒室聲學模型中，成功預測該燃燒室最易發生不穩定燃燒的頻率為1 389.9 Hz，且不同擾動振幅下，燃燒室的（n=1，m=1，j=1）模態均穩定，不會發生不穩定燃燒現象，與試驗結果一致。