基于調制函數的振動力學模型全參數估計
陳宇寧, 吳建民, 田 楊
(1.上海工程技術大學 機械與汽車工程學院, 上海 201620;2.沈陽理工大學 機械工程學院, 遼寧 沈陽 110159)
應用力學模型進行系統的力學特性分析,是揭示系統振動規律從而進行結構設計與改進的重要方法,而獲得精準的動力學模型參數是建模過程的關鍵技術。為此,學者們針對動力學模型參數估計進行了相關研究。孔令毅等[1]應用增廣最小二乘法完成了動力學模型參數的無偏估計。王茜等[2]聯合全相位FFT和最小二乘法建立了電機葉片的振動參數估計模型。吳超等[3]搭建了電磁軸承-柔性轉子系統實驗平臺,并基于模態實現了動力學模型的參數辨識。高軒等[4]采用分步辨識法建立系統力學蠶食辨識模型。魏青軒等[5]將離散頻譜校正和最小二乘聯立,推導了以加速度信息為輸入的系統參數辨識模型。李新廣等[6]結合了Fourier級數方法和最小二乘法辨識出非線性動力學模型中的剛度與阻尼。商興蓮等[7]利用多體系統傳遞矩陣法識別出機床動力學參數值。
上述方法通過實驗或理論方法進行了動力學參數的估計,然而上述方法沒有實現剛度、阻尼和力的全參數估計,課題組基于調制函數法提出了一種具有通用性的動力學參數辨識方法,通過該方法可實現動力學全參數的估計。
1 動力學模型參數估計
振動分析過程經典力學將系統視為如圖1所示的力學模型。
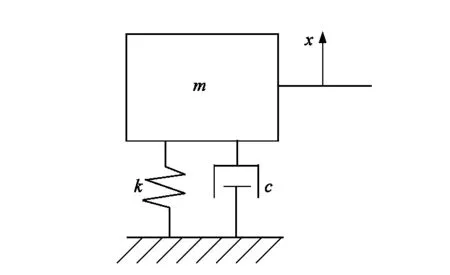
圖1 動力學系統模型Figure 1 Dynamic system model
上述動力學模型可描述為[8-10]:
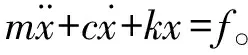
(1)
式中:m為質量,c為阻尼,k為剛度系數,f為作用力。
由于加速度傳感器便于布置,且其為相對式儀器,基于加速度信息估計動力學模型參數,則有:
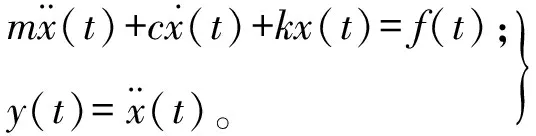
(2)
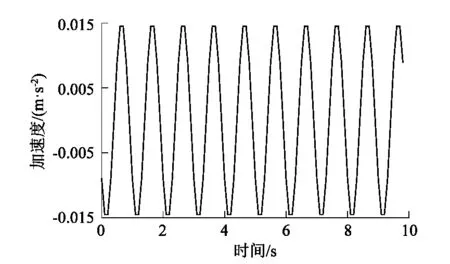
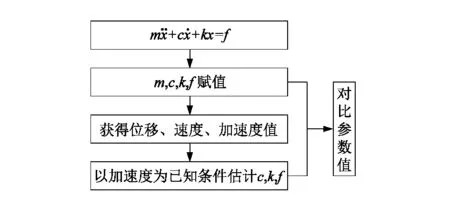
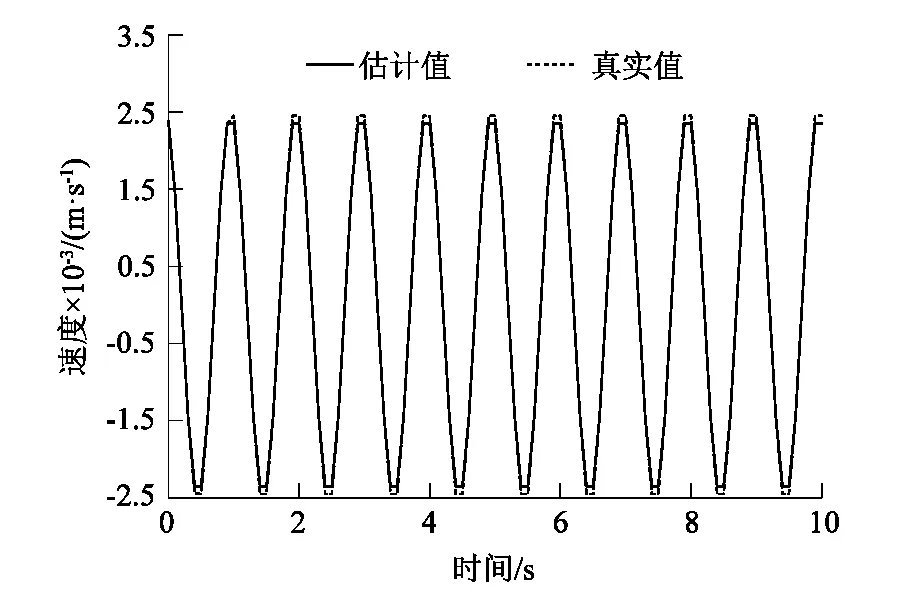
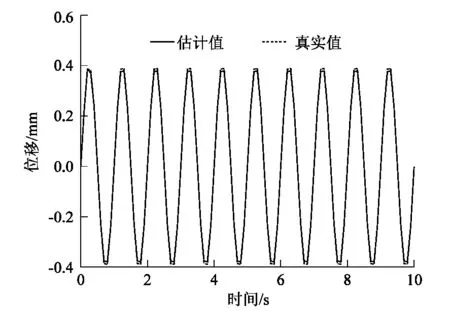
設T (P1)∶g∈Cl([t-T,t]); 式中:t為時間,T為任意小于時間t的常量。 (3) 式中:τ為在定義域內的參數,pj為冪函數,ρj為對應階次的常數。 然后將模型近似如下: (4) (5) 在式(5)中使用分部積分可得到: (6) (7) 根據調制函數gi的性質,其未知邊界值可以被消除,因此,對于i=1,…,N,可以得到: (8) 其中: Aλ=b。 (9) 式中b為常向量。λ=(c,k)T,A∈RN×2和b∈RN如下: 式中i=1,…,N。 式(9)可以用最小二乘法求解,得: λ=(ATA)-1ATb。 (10) 為了估計參數力f,課題組考慮雅克比正交基,定義在[0,1]上的雅克比正交多項式如下: (11) 式中μ,κ∈[-1,+∞]。 令函數f和g是屬于C([0,1])的函數,然后是標量積〈·,·〉μ,κ函數的定義如下: (12) 式中ωμ,κ(τ)=(1-τ)μτκ是相關的權重函數,因此可以獲得: (13) 如果f∈C([t-T,t]),其可以用下面的雅克比正交級數來表示: (14) 為了驗證上述模型的準確性,課題組應用MATLAB編制了式(1)動力學方程的計算程序,通過代入已知作用力,已知動力學模型參數剛度k、阻尼c和作用力參數f,計算出在此作用力f下的位移、速度和加速度: f=F0sinωt。 (15) 式中F0為常力。 系統動力學模型中部分參數如表1所示。 表1 力學模型參數Table 1 Mechanical model parameters 通過計算可獲得模型的位移、速度和加速度信息,而課題組提出的估計模型是以加速度信息作為輸入的,因為在布置傳感器的過程中,加速度傳感器更容易完成裝配,計算出的加速度信息如圖2所示。 圖2 加速度真實值Figure 2 True value of acceleration 在已知加速度的前提下,將模型真實參數剛度k、阻尼c和作用力參數f作為未知參數,應用式(2)~(13)估計得到剛度k、阻尼c和作用力參數f,再將估計值與真實值進行對比,從而驗證參數辨識模型的正確性,具體驗證過程如圖3所示。 圖3 估計方法驗證流程Figure 3 Estimation method validation process 按照圖3的流程通過仿真估計出參數:k=3.85×107N·m-1;c=4.59×104N·s·m-1;f=14 750 sinωt。仿真估算得到k,c,f,與表1中的真實值對比,誤差分別是1.3%,2.0%和1.7%。 為了進一步直觀地對比課題組提出估計模型的準確性,課題組將估計出的參數代入式(1)中重新計算出系統速度和位移的估計值,圖4所示為速度的真實值與估計值對比結果。 圖4 速度的真實值與估計值對比Figure 4 Comparison of real and estimated speed 圖5所示為位移的真實值與估計值對比結果。 圖5 位移的真實值與估計值對比Figure 5 Comparison of real and estimated displacement 通過對比可知:在應用估計出的參數進行動力分析的估計值與真實值重合度較高,其趨勢重疊且振動幅值誤差較低,因此證明課題組提出估計模型具有較高的精度。 課題組以便于獲得的加速度信息為輸入數據,基于傳統動力學模型通過調制函數法建立了振動力學系統的全參數的估計模型,所提出的方法將微分問題轉換為積分問題,大大降低了求解的誤差,通過估計值和真實值得對比,其綜合平均誤差為1.67%,通過課題組提出的估計模型,可實現振動力學參數無法測量前提下的系統建模,從而開展相關的力學狀態分析。
(P2)∶g(k)(t-T)=0;
(P3)∶g(k)(t)=0。1.1 剛度和阻尼參數估計
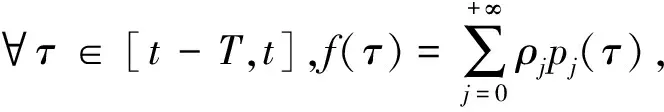
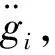
1.2 參數力f的估計
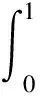
2 模型驗證

4 結論

