基于2UU-UPU并聯機構的4足機器人設計

賈云博， 許 勇， 杜靜恩， 施浩然， 賴磊捷， 徐 蕊

(上海工程技術大學 機械與汽車工程學院， 上海 201620)

隨著科學技術的發展，一些危險環境下的工作和人類無法完成的任務都可以由機器人來替代。足式機器人是模仿動物的運動模式來進行設計的，足尖可以在工作空間內選擇合適的支撐點，在多種地形有著良好的通過性，在復雜地形中能以合適的步態穩定行走。而多足機器人中，4足機器人由于其穩定性好，負載能力強，適應性良好，成為發展前景非常廣闊的特種機器人之一，廣泛應用于搶險救災、軍事偵查、地質探測和智能服務等領域[1-2]。因此近年來很多學者和研究機構針對4足機器人進行了深入的研究。

美國波士頓動力公司研制的Big Dog 4腿機器人[3-4]，可以承載重物，且具有較快的移動速度和較強的平衡能力，最初設計目的是用于軍事方面。日本東京工業大學 Ota研發了一種輕量化的并聯移動機器人 Para-walker[5]，采用串并混聯機構使其具有更大的工作空間和更穩定地移動。北京理工大學王軍政等研發的哪吒4足機器人[6]，采用了6-SPS并聯機構設計腿部結構，并將動平臺作為移動機器人的足端。由于6-SPS并聯機構具有6個自由度，因此哪吒機器人具有很高的自由度與靈活性，但是由于每條腿都有6個自由度，所以至少需要6個驅動來實現運動，控制難度較高。

目前，4足機器人的研究向高負載、高靈活性和高智能化發展。已有的大多數4足機器人采用串聯腿的設計結構，優點是靈活性好，缺點是負載方面存在不足。課題組提出一種將并聯機構2UU-UPU作為腿部基本構型的4腿機器人，使其具有負載大、環境適應性強的特點。以此為研究目標，首先對單條腿中的并聯機構進行自由度分析，建立坐標系以及求該機構的逆解表達式；進而求得該機構的工作空間，驗證該機構作為腿部運動構件的可行性；最后進行4足機器人的步態規劃和仿真分析。因此，該課題的研究具有重要價值和工程實際意義。

1 4足機器人新型并聯腿機構構型

課題組提出的4足機器人新型并聯腿機構如圖1所示。它包括大腿和小腿2部分：大腿部分由2UU-UPU并聯機構組成，包括1個與機器人身體相連的上平臺，1個與小腿固接的下平臺，上下平臺為2個全等的等邊三角形，上下面之間有3條支鏈，包含1個UPU支鏈和2個UU支鏈；小腿與下平臺的夾角為45°。采用至少3個電機對該腿部結構進行驅動：其中1個位于驅動UPU支鏈的P副沿著桿長方向移動；另外2個設置在2個UU支鏈靠近上平臺的U副上，2個電機的驅動方向是垂直的。

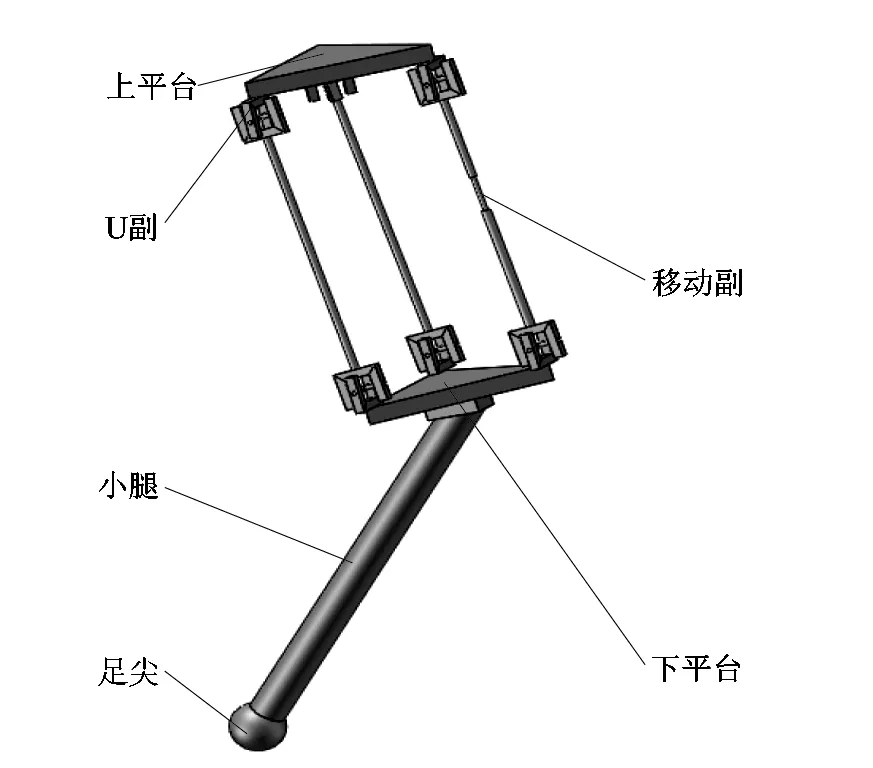
圖1 新型并聯腿機構三維構型Figure 1 3D configuration of new parallel leg mechanism

4足機器人的關節配置對于整個機器人的性能起至關重要的作用，合理的關節配置可以讓4足機器人的穩定性更好，靈活性更高，復雜地形適應能力也會更強。目前有如下4種關節配置方式：①前后膝式；②前膝后肘式；③前后肘式；④前肘后膝式。如圖2所示。4種結構各有利弊，可根據不同的需求選用不同的結構。根據前人的研究[7-8]，前肘后膝式結構緊湊，足底與地面的滑動較小，靈活性較高，適合大負載結構，因此選擇前肘后膝式。

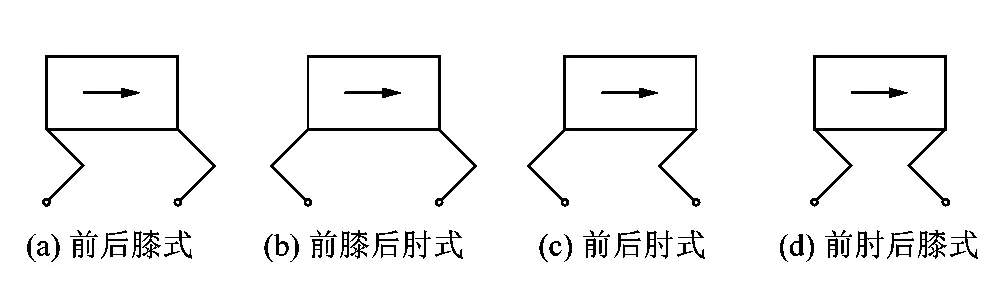
圖2 4足機器人腿部關節配置Figure 2 Joint configurations of quadruped robot legs

2 并聯腿機構自由度計算

據Grubler-Kutzbach準則[9]，自由度求解公式為：

(1)

式中：d為階數，取值5；n為構件數，取值6；g為運動副數，取值7；fi為第i個運動副的自由度數，ν為冗余自由度，取值0；ζ為局部自由度，取值0。

對于2UU-UPU機構，虎克副的自由度為2，移動副的自由度為1，將以上的數據代入式(1)中可以得出F=3。即2UU-UPU機構的自由度為3，該2UU-UPU并聯機構的自由度始終為2個轉動加1個移動。

3 位置逆解求解

圖3為并聯腿的幾何模型。在A1點處建立空間直角坐標系O-XYZ，X軸與A1A2平行，上平臺在O-XY面內，Z軸與O-XY面垂直；移動坐標系o-xyz位于足尖的中心，其中x軸與B1B2平行，z軸沿co方向。co與平面B1B2B3的夾角α為45°，并且在點c處與B3D相交，點D是B1B2的中點。2-UU-UPU并聯腿的逆運動學是通過已知足尖的坐標o=(x0，y0，z0)的情況下求輸入參數，即U副在2個互相垂直方向上的轉動角度和移動副P的移動距離。

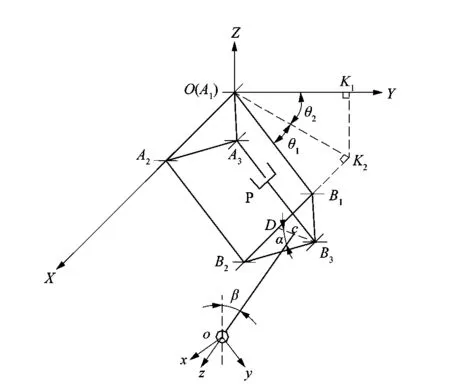
圖3 并聯腿機構的運動學模型Figure 3 Kinematic model of parallel leg mechanism

A3在空間直角坐標系O-XYZ中坐標可表示為

(2)

式中：l1為上下平臺2個全等等邊三角形的邊長，A3為上平臺與移動副相接的U副中心點。

U副在2個互相垂直方向上的轉動角度為θ1和π/2-θ2，因此可求得B1點的坐標：

B1=(l2·sinθ1,l2·cosθ1·cosθ2,l2·cosθ1·sinθ2)。

(3)

式中：l2為A1B1和A2B2的長度，θ1為A1B1到面O-ZY的夾角，θ2為A1B1到面O-XY的夾角。

由B1知D點的坐標為

D=(l2sinθ1+l1/2,l2cosθ1cosθ2,l2cosθ1sinθ2)。

(4)

足尖o和D在X軸上的坐標相同，根據xB1+lB1D=x0可得

(5)

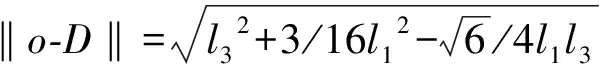
(6)

其中：

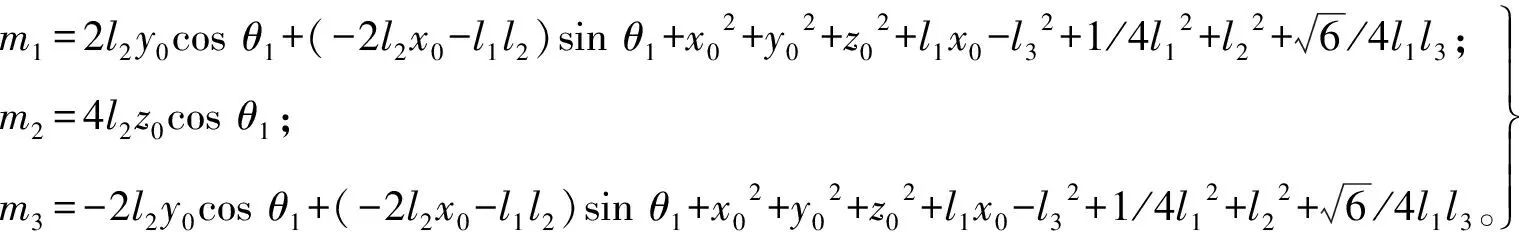
(7)

B3和D在基坐標系中的坐標可表示為：

(8)

(9)

式(4)和式(9)是D點坐標在不同坐標系中的表示方法，因此可求得β。可由‖B3-A3‖=d1求得

(10)

由式(5)、(6)和(10)可知，在足尖運動軌跡給定的情況下可求得驅動函數。

4 并聯腿機構足端工作空間求解

機器人的工作空間是指機器人末端執行器上的參考點(即圖3中o點)所能達到的空間點的集合。對于足式機器人來說，求解工作空間是一項十分重要的指標，直接影響到機器人的運動性能，根據得到的工作空間的形狀來判斷腿部構型是否達到機器人的運動要求。機器人的工作空間有3種類型：可達工作空間、靈巧工作空間和全工作空間[10]。后續的研究需要考慮到足尖所能達到的最大運動范圍，因此課題組選用可達工作空間；基于求得的運動學逆解，在MATLAB中利用坐標搜索法求解并聯腿的工作空間。

4.1 工作空間求解步驟及參數設定

在求解該并聯機構的工作空間前，首先要確定其結構約束條件和設定必要的結構參數，在約束條件的范圍內進行搜索。

1) 參考4足動物的關節比例，將腿部的2個關節設計為等長結構，根據設計目標可得腿部結構參數：l1=5 cm，l2=l3=40 cm。

2) 由結構參數和運動學逆解，并經調試后確定X、Y和Z軸搜范圍為：-40 cm≤X≤50 cm，-60 cm≤Y≤40 cm，-90 cm≤Z≤0 cm，搜索步長為1 cm。

3) 由于腿部機構的結構較為緊湊，為避免運動過程中發生干涉，限定θ1的活動范圍為-9π/20≤θ1≤9π/20，θ2的活動范圍為19π/20≤θ2≤π/20。

4) 為保證腿部與身體垂直的方向上有較大的運動范圍，A3B3上移動副d1的搜索范圍為35 cm≤d1≤45 cm。

5) 另外足尖的高度不應高于B2點的高度， 因此z≤l2·cosθ1·sinθ2。

4.2 足端工作空間求解結果

結合運動學逆解式(5)，(6)和(10)，使用邊界搜索算法，并輸入參數和約束條件，在MATLAB中進行編程可以得到圖4所示的4足機器人單足工作空間及其在3個坐標平面上的投影。

圖4(a)為4足機器人單足工作空間；圖4(b)為工作空間在XOY面上的投影；圖4(c)為工作空間在ZOY面上的投影；圖4(d)為工作空間在ZOX面上的投影。從圖中可以看出，腿部工作空間形狀飽滿，在XYZ軸上的工作長度較大，適合于并聯機械腿實現多種形式的步態，在行走時可以實現較高的抬腿高度和較大的步長。

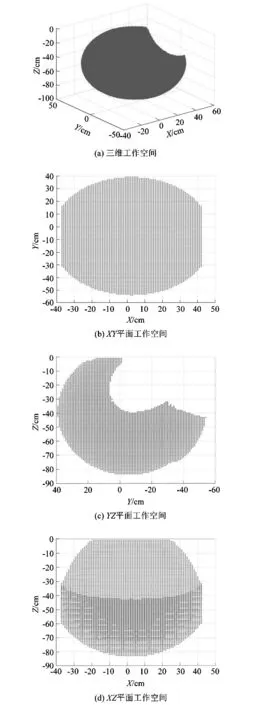
圖4 并聯腿機構足端工作空間Figure 4 Foot workspace of parallel leg mechanism

5 步態規劃與仿真

5.1 4足機器人建模

在SolidWorks三維建模軟件中建立4足機器人的模型，為了使仿真更方便，求解速度更快，因此要對4足機器人的結構模型進行簡化。圖5所示為能滿足腿部并聯機構運動特征的4足機器人模型，由身體部分、左前腿、左后腿、右前腿和右后腿組成。對模型進行材料設定，并將模型以x_t格式進行保存，為下一步在ADAMS軟件中進行虛擬樣機仿真做準備。

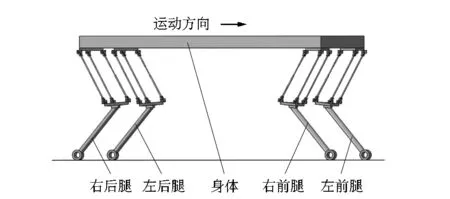
圖5 4足機器人模型Figure 5 Quadruped robot model

5.2 4足機器人步態規劃

為了滿足4足機器人在不同環境下能穩定移動，需要采用不同的步態。常用的步態有三角步態、對角步態、溜蹄步態和跑跳步態等[11]。在較為平坦的路面上行走時，對角步態較為常用，可以提高機器人的行進速度，并且具有良好的穩定性。在對角步態中，機器人的邁腿順序為：右前腿和左后腿同時邁出1步，落地之后，左前腿和右后腿再同時邁出，同樣的邁腿方式循環下去，就構成了對角步態。

4足機器人對角步態示意圖如圖6所示，箭頭所指為機器人運動方向，L1，L2，R1和R2分別為左前腿、左后腿、右前腿和右后腿，虛線為前一步的動作，從圖6(a)到圖6(b)為L2和R1向前運動，L1和R2此時為支撐腿；從圖6(b)到圖6(c)為L1和R2向前運動，L2和R1此時又為支撐腿。在對角步態中，由于運動時誤差的出現，以及環境的影響，整個機器人的質心無法始終處于機身的對角線上[12]，需要仿真分析來驗證其穩定性。

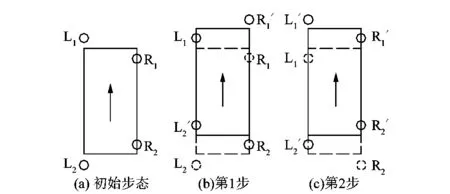
圖6 4足機器人對角步態示意圖Figure 6 Diagonal gait of quadruped robot

為了使足端在與地面接觸時不產生滑動，以及具有較小的反作用力，抬腿和落地時的速度應為0，因此在Y軸方向(即機器人運動方向)上采用復合擺線進行足尖步態規劃[13]，4足機器人擺動腿的足端軌跡為：

x(t)=S(t/T-1/(2π)*sin (2πt/T))-20；

(11)

z(t)=H(1/2-1/2*cos (2πt/T))-70。

(12)

式中：S為4足機器人的步長，H為抬腿高度，t為采樣時間，T為步態周期。

根據求得的機器人單足工作空間，設S=35 cm，H=20 cm，T=0.4，在MATLAB中畫出擺動腿的軌跡，如圖7所示。支撐腿與地面無滑動的前提下，推動機器人身體向前移動，此時支撐腿足端軌跡反向水平后移，因此其在Z軸方向上的位移始終為0，可利用機器人逆運動學獲得各驅動的驅動函數。

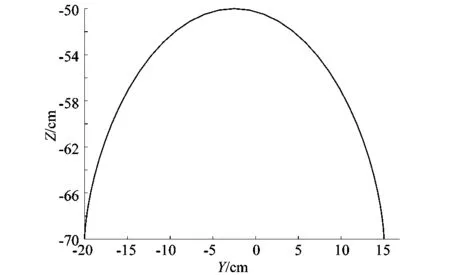
圖7 并聯腿機構足端軌跡規劃Figure 7 Foot trajectory planning of parallel leg mechanism

5.3 虛擬樣機仿真與分析

將5.1節所述的4足機器人模型導入ADAMS，建立虛擬樣機模型，如圖8所示。根據機構的運動關系，添加53個運動副和約束，以及12個驅動，4足機器人在環境中受到重力和與地面的相互作用力，因此設置每1 kg物體重力大小為9.8 N,方向沿Z軸正方向，在足端和地面之間建立接觸力，接觸力參數設置如圖9所示。

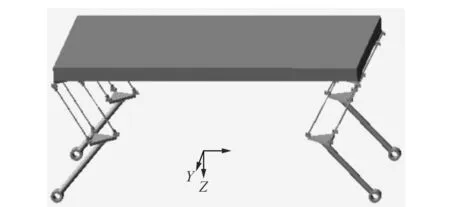
圖8 4足機器人虛擬樣機模型Figure 8 ADAMS model of quadruped robot

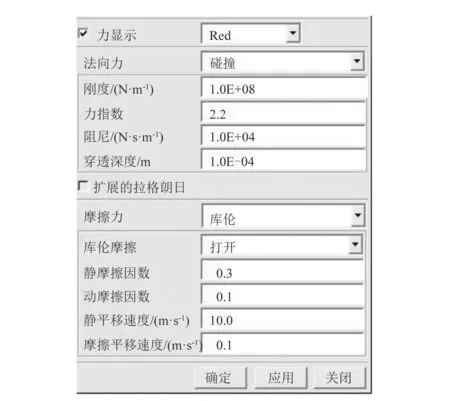
圖9 接觸力參數設置Figure 9 Contact force parameter setting

在每條腿動平臺上的U副以及移動副上添加驅動以及驅動函數，開始進行仿真。仿真結束后，在后處理模塊中可以獲得仿真結果并輸出仿真曲線。4足機器人的質心在X軸、Y軸和Z軸3個方向的位移曲線分別如圖10所示。X軸方向為機器人的前進方向，可以看出前進位移軌跡增長比較平穩，質心在Y軸和Z軸方向有一定的波動，波動幅度較小，說明整個運動過程機器人可以穩定行走。

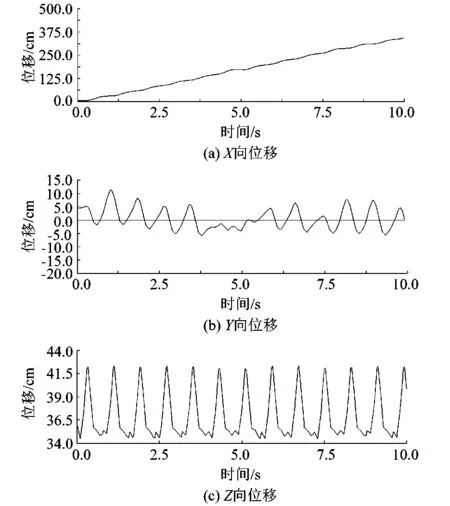
圖10 機器人整體質心位移仿真曲線Figure 10 Displacement simulation of global centroid of quadruped robot

6 結論

課題組設計了一種基于2UU-UPU并聯腿結構的新型4足機器人，通過對2轉動1移動自由度的驅動，使腿部具有較高的靈活度，控制也較為方便。通過運動學逆解，以及單腿結構工作空間的分析，證明了該機構作為4足機器人腿部結構具有理想的工作空間，為進一步進行步態設計及優化奠定了基礎。利用ADAMS對所設計的新型4足機器人進行動力學仿真，結果表明驅動函數以及步態規劃合理，可以達到穩定行走的目的。

后續可針對多模式步態以及控制函數的優化進行研究，以應用于資源探測、危險環境采樣等多種環境工作。因此利用2UU-UPU結構作為腿部的4足機器人具有進一步研究的價值。