基于IFWA-PNN 的變壓器故障診斷研究

張邵杰，朱 武

（上海電力大學電子與信息工程學院，上海 201306）

變壓器是電力系統中的關鍵設備[1]。變壓器一旦發生故障會嚴重威脅電力系統的正常運轉，造成重大經濟損失，因此準確快速地預測變壓器故障對維護電網安全和保障人民財產安全具有重要意義。隨著技術的發展，電網的規模及復雜度不斷擴大，傳統故障診斷方法在診斷準確度和診斷速度上的缺點越發明顯。眾多學者開始將傳統算法與神經網絡結合進行故障診斷。文獻[2]、[3]利用算法與BP 神經網絡相結合，證明了神經網絡在變壓器故障診斷中是可行的，但BP 神經網絡本身收斂效果不佳。文獻[4]利用了PNN 網絡結構完成了變壓器故障診斷，提升了準確率，相比BP、RBF 網絡，PNN 訓練速度快，結構簡單，容錯性好且更加適合故障分類[5]。

為了更快地獲取PNN 網絡的平滑因子，眾多的智能算法用于優化PNN 網絡。有學者提出的煙花算法，相比粒子群算法收斂速度快，更適合全局搜索。文獻[6]針對爆炸幅度進行改進，提出動態爆炸半徑算法，使算法搜索性改善，但煙花交互能力沒有變化[7]。文獻[8]進一步平衡了局部搜索和全局搜索。本文結合改進算法的優點，主要采用改變變異算子的方式改進煙花算法，進而優化PNN 網絡。

1 煙花算法及改進

根據煙花爆炸現象，有學者于2010 年提出煙花算法[9]（fireworks algorithm，FWA），其基本思路是通過煙花爆炸產生的火花，實現鄰域搜索最優解。煙花算法的魯棒性較強，全局優化性能好，易于實現，收斂速度快，具有爆發性和隨機性等顯著特點[10]。煙花算法主要包括4 部分，分別是爆炸算子、變異算子、映射規則和選擇策略，其中爆炸算子包括爆炸強度、爆炸幅度和位移操作。煙花在每次爆炸時都生成相應火花，適應度好的煙花，爆炸強度大，生成火花數量多；適應度不好的煙花，爆炸強度小，生成火花數量少。為使算法盡可能探索搜尋整個可行解的空間，爆炸生成的火花數目和爆炸半徑計算方式分別如公式（1）和公式（2）所示：

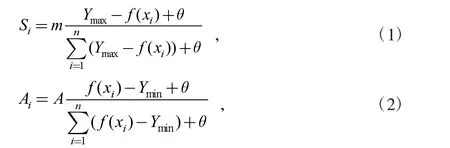
其中：Si為第i 個煙花爆炸火花的數量，m 為控制煙花產生火花總數的參數，Ymax=max（f（xi））（i=1，2...n）是n 個煙花目標函數的最大值，Ymin是n 個煙花目標函數的最小值。A 是常數，θ 為常數，避免分母為0 錯誤。

在FWA 算法中，采用高斯變異對煙花選取若干維度進行操作，這樣不利于確保火花的多樣性。EFWA 提出在當前解與當前種群種最好的個體進行變異，使得一個煙花不僅可以在附近搜索，還可以在較遠處搜索。參考差分進化算法中的變異算子，本文使用差分向量作為變異操作，如公式（3）所示：

其中：xi為當前代最優個體，xj、xk為隨機選擇的兩個解，p和q 為常數，本文中p=0.5，q=0.05。

煙花算法的選擇策略是基于距離的，隨著迭代次數的增加，所有煙花都逐漸靠近最優個體，降低了煙花的多樣性，導致算法收斂效果不理想。本文采用隨機選擇的方式保證算法的種群多樣性。

為驗證改進算法的性能，采用Rastrigin 測試函數（全局最小值為0，表達式如公式（4）所示）分別對煙花算法和改進煙花算法做性能測試，如圖1 所示，證明改進煙花算法能更快收斂且準確度高。

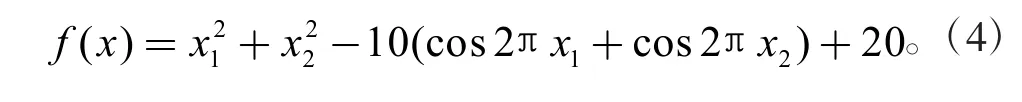
圖1 改進煙花算法與標準煙花算法收斂曲線對比測試

2 PNN 神經網絡

概率神經網絡（PNN）是一種典型的前饋神經網絡，是由貝葉斯分類規則發展而來的一種網絡結構。自PNN神經網絡提出以來，由于其結構簡單，訓練簡潔，在實際應用中，尤其是在分類問題上得到了廣泛應用。PNN 網絡能有效地處理非線性數據，能夠將故障樣本空間和故障模式空間建立聯系，有效處理非線性數據。PNN 神經網絡由輸入層、模式層、求和層和輸出層4 層構成，其結構如圖2 所示。

圖2 PNN 結構模型

輸入層神經元個數為特征向量個數，該層計算輸入向量與樣本向量間的距離。模式層的作用是將類似樣本集中到一起，激活函數通常采用高斯函數，該層依據公式（4）計算故障特征向量與訓練集中故障類型匹配關系。求和層相當于一個加法器，將模式層輸出相似度相加，得到故障類型概率密度函數式。輸出層相當于比較器，按最大概率輸出結果。

其中：X 為特征向量，Wi為輸入層與模式層的連接權值，σ 為平滑因子。診斷過程中平滑因子是極其關鍵的參數，需要不斷嘗試確定一個最優值。

PNN 網絡具有很好的兼容性，輸入層神經元個數對應特征向量個數，求和層神經元個數對應故障類型個數。相比BP 神經網絡，PNN 更適合解決分類問題，具有較強的抗干擾性，數據樣本容量對系統的影響很小。此外，PNN 分類性能受樣本相似度的影響，樣本相似度分析通常采用歐氏距離、余弦距離和馬氏距離等。其中，歐氏距離側重空間距離，余弦距離側重角度距離。

PNN 更適合解決分類問題，具有較強的抗干擾性，數據樣本容量對系統的影響很小。PNN 故障診斷性能對平滑因子σ 依賴嚴重，如何確定參數取值是提高其性能的關鍵。本文采用改進的FWA 優化PNN 的平滑因子，以提高PNN 故障模式識別精度。IFWA-PNN 算法步驟如下：

（1）導入訓練樣本，初始化煙花位置和參數。

（2）計算適應度，尋找當前最優位置，生成下一代火花位置和數目。

（3）更新煙花位置，評價適應度。

（4）判斷是否滿足尋優條件，若滿足，輸出最佳平滑因子，若不滿足，重復（2）、（3）和（4）步驟。

（5）將最佳平滑因子導入PNN 模型，形成改進FWAPNN 診斷模型。

（6）導入測試樣本，判斷模型故障診斷準確率。

3 變壓器故障診斷實驗

3.1 數據處理及樣本選擇

影響變壓器故障的油中溶解氣體有很多種，其中影響較大的有氫氣（H2）、甲烷（CH4）、乙炔（C2H2）、乙烯（C2H4）和乙烷（C2H6）5 種，這5 種氣體貢獻了絕大部分故障信息[11]，根據三比值法，采用C2H2/C2H4，CH4/H2和C2H4/C2H6作為特征輸入量，為了避免數據大小不一，影響概率神經網絡的故障判決，利用公式（5）對數據進行歸一化處理，得到歸一化數據。

其中：xi為原始數據，xmin、xmax分別是對應數據最小值和最大值。

故障類型分為5 種，包括正常、中低溫過熱、高溫過熱、高能放電和低能放電，因此網絡輸入層神經元個數為3，輸出層神經元個數為5。為了方便統計，對各故障類型進行編號（見表1）。本文共采集200 組變壓器故障數據，其中140 組用作訓練，60 組用于測試。各故障類型樣本和測試數目見表1。

表1 各故障類型編號和樣本數目

3.2 模型實驗

在MATLAB 實驗平臺下，將故障樣本數據導入改進FWA-PNN 診斷模型中進行正確率測試。結果如圖3 所示，共有5 組數據判斷錯誤，其中中低溫過熱和低能放電2 種故障判斷準確率為100%，正常情況有1 組判斷錯誤，高能放電和高溫過熱各有2 組數據判斷錯誤，綜合準確率為91.7%。

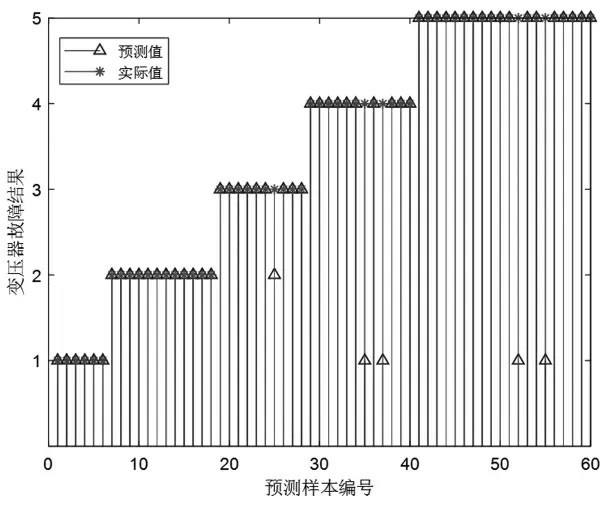
圖3 IFWA-PNN 診斷模型預測結果

為了更好地說明該機算法的優越性，并將同樣條件下的樣本分別導入FWA 優化PNN 模型[12-13]，PNN 模型及SVM 分類模型中做正確率預測并將4 種方式正確率作對比[14-15]。表2 給出了各診斷模式下測試樣本準確率。

結合表2 的實驗數據，可以看出改進FWA-PNN 診斷模型明顯提高了故障診斷準確率。傳統的SVM 診斷模型準確率只有73.3%，PNN 分類診斷準確率有83.3%，FWA 優化的PNN 診斷模型準確率有86.7%，而經過改進FWA 優化的PNN 故障診斷模型準確率達91.7%。對比傳統的SVM 診斷模型，改進FWA 算法對變壓器故障診斷有明顯效果，尤其是對正常狀態、高溫過熱狀態2 種故障提升效果明顯。結果表明，改進FWA 算法能優化概率神經網絡的平滑因子，提升網絡的故障分類性能，進一步證明了算法的優越性。

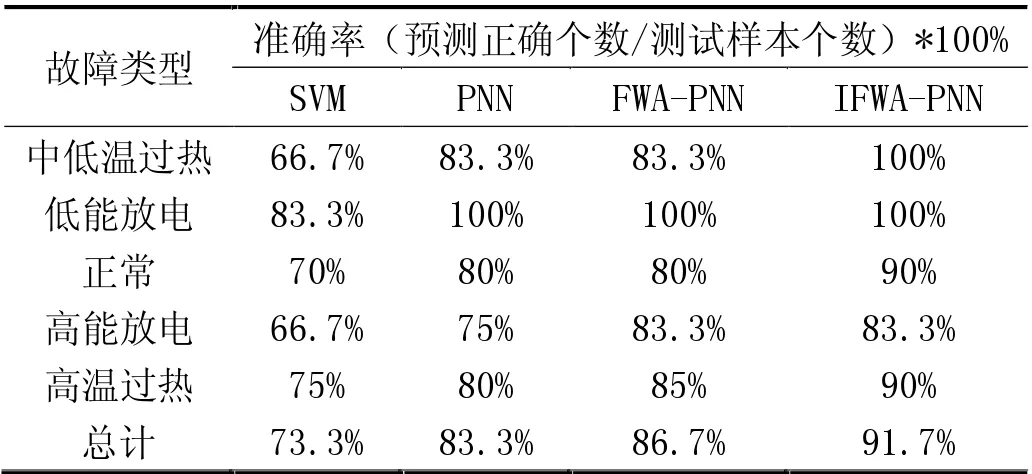
表2 各種診斷模式下測試樣本準確率

4 結束語

由于PNN 網絡故障分類時平滑因子難以確定，且標準煙花算法存在一定缺陷，筆者采用改進的煙花算法優化PNN 網絡的平滑因子，并用于變壓器故障診斷中。經驗證，改進的煙花算法優化PNN 網絡相比實現了變壓器故障分類，相比SVM，PNN 診斷模式更是顯著提升了準確率，表明該診斷模型的有效性和實用性。