基于MATLAB 的軌道車輛幾何曲線通過計算

麻岳敏，聶 敏，武學良，朱凱博

（中車大同電力機車有限公司 技術中心，山西大同037038）

我國1/3 的鐵路線是曲線，因此，機車在設計過程中必須進行幾何曲線通過計算，以保證機車順利通過小半徑曲線和滿足限界要求。確定機車所能通過曲線的最小半徑和為此目的所需的輪對橫動量，給出機車轉向架通過曲線時的轉心位置，確定在曲線上機車轉向架對于車體的偏轉角，以及車體與建筑限界的關系等［1］是重中之重。為了提高行車質量，許多學者和工程人員對這些問題進行了深入的研究。

目前工程設計人員主要采用幾何作圖法、幾何公式計算法和參數化計算法來求解幾何曲線通過。劉冰等［2］對這幾種設計方法的優缺點進行了對比分析。羅仁等［3］結合繪圖法得到車輛通過不同曲線時的姿態，分析了車輛連掛狀態通過圓曲線S 形曲線等工況下車鉤轉角。李強等［4］給出了車體和轉向架相對轉動角度和車鉤轉角的幾何公式，但在有含直線的S形曲線上沒有給出解析解。聶敏等［5］運用解析幾何的基本理論，推導出有軌電車通過平面曲線、豎曲線時鉸接裝置轉角及車鉤夾角的計算方法。王璐科［6］引入“等效曲線半徑”概念，簡化了原本復雜的考慮轉向架偏移的機車車輛曲線通過計算。王文濤等［7］使用AutoLISP 和DCL 語言編制出機車幾何曲線通過計算程序實現了自動計算及參數化繪圖。丁長權等［8］介紹了基于VB 的車輛幾何曲線通過參數化計算方法，求出了轉向架與車體最大的相對轉角。商躍進［9］利用在SolidWorks 平臺下的尺寸驅動特性和方程式功能建立了B0-B0軸式軌道車輛幾何曲線通過計算模板，求出了給定參數下的車體與轉向架最大夾角。文獻［7-9］利用參數化計算方法計算了車體和轉向架的轉角，但沒有給出車鉤轉角的算法，也沒有計算可通過的最小曲線半徑。

針對上述問題，文中利用MATLAB 強大的功能，提出一種基于MATLAB 的軌道車輛幾何曲線通過計算方法，實現求解車鉤轉角和最小曲線半徑的簡便化和可視化。

1 計算原理

1.1 幾何曲線通過

1.1.1 車鉤轉角的計算[5]

機車通過曲線時，相鄰兩車輛的中心線將會出現相對轉動，車鉤中心線相對車體也會出現相對轉動，產生的相對運動會影響車輛運行平穩性和安全性。因此，在新車型設計時，需要計算連掛車輛通過曲線時的車鉤轉角和對應的輪對橫動量，避免產生干涉以確保列車能夠安全通過曲線。利用“等效曲線半徑”來求解車鉤轉角，如圖1 所示，在該計算中假設相鄰接車鉤不能相對轉動，始終在一直線上，且相鄰兩車鉤旋轉中心距離不變。

圖1 機車過曲線示意圖

根據幾何關系求解車鉤轉角為式（1）、式（2）：

式中：γ1和γ2是車鉤轉角，∠PBO、∠OBC、∠OCQ、∠OCB是和兩節車體輪對總橫動量有關的參數。

PA、PA′、QD、QD′表示車體中心到轉向架中心之距；AB、A′B′、CD、C′D′ 表示轉向架中心到車鉤旋轉中心之距；BC表示兩車鉤旋轉中心之距；OP、OQ表示曲線中心到車體中心之距；AA′和DD′表示車體總橫動量。

通過這2 個方程可以在車體輪對橫動量已知的情況下，求出車鉤轉角；也可以已知一個車鉤允許的最大轉角，求出另一個車鉤轉角和車體輪對橫動量（默認2 節車的輪對總橫動量相同）。

1.1.2 機車能通過的最小曲線半徑[1]

轉向架式機車能夠通過的最小曲線半徑，受限于轉向架在構造上允許的最大轉角。當機車通過曲線時，轉向架相對于車體產生的轉角，曲線半徑越小，轉角越大。當兩轉向架各自的端軸用盡了橫動量之后，各轉向架以外端軸貼靠外軌，內端軸貼靠內軌，此時為機車通過最小曲線半徑Rmin時的情況。為了簡便且考慮安全裕量，假定各軸均無橫動量，根據幾何關系，可求出可通過的最小曲線半徑為式（3），如圖2 所示。

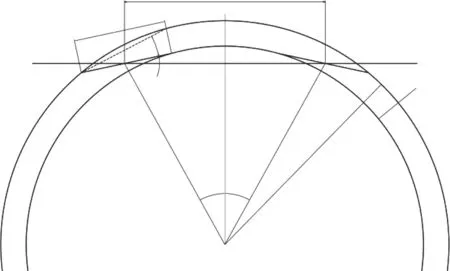
圖2 機車通過最小曲線半徑的示意圖

式中：a為轉向架中心距；θ′為轉向架構造上允許的最大轉角；θ表示轉向架輪對分別靠內外軌產生的角度，為式（4）：

式中：p為轉向架軸距；σ+Δ 為輪緣與鋼軌的總間隙。

1.2 MATLAB 參數化

MATLAB 是功能全面、操作直觀和簡潔的數據計算和處理的計算軟件，其數學計算方面功能相當強大，實現及驗證算法非常便利，同時具有非常強的編程和結果的可視化功能。文中利用MATLAB 自身的函數來求解幾何曲線通過，利用GUI 來可視化。每一個GUI 界面對應著一個M 文件，根據數學模型，編輯相應的M 文件，在GUI 界面輸入初始條件，點擊運行，得到結果。通過GUI，用戶就可以不需要輸入任何的腳本或命令，不需要了解任務的內部運行方式，只要用鼠標點擊系統窗口中的按鍵，就可能輕松得到想要的結果。

幾何曲線通過計算界面分為3 個模塊，可分別去計算求解，它們之間互不干涉，每1 個模塊都可單獨生成研究報告，如圖3 所示。模式1 是已知輪對總橫動量求車鉤轉角，模式2 是已知最大一車鉤轉角求另一個轉角和輪對總橫動量，模式3 是求可通過最小曲線半徑。可視化界面還設置了工具欄，放一些常用的工具以方便操作者使用。

圖3 幾何曲線通過GUI 界面

MATLAB 提供了一系列的畫圖函數，用戶不需要過多的考慮畫圖的細節，僅僅給出一些基本參數就能得到所需圖形。繪制幾何曲線求車鉤轉角圖原理：以O點為坐標原點（0，0）。根據給定的參數，來確定點P、B、C、Q的坐標，然后將其各點依次連接，再根據向量內積和向量長度計算出車鉤轉角。最后通過輸出函數將結果顯示在圖上。繪制求最小半徑圖原理：根據數學公式，輸入運行參數，得到最小半徑值。將各點的坐標值通過畫圖函數連接起來，最后通過輸出函數將結果顯示在圖上。

MATLAB 可以將編制好的獨立可執行程序發布為后綴.exe 的應用程序，此程序可脫離MATLAB 環境獨立運行。為了便于本程序的傳播和交流，最后將本程序發布為后綴.exe 的應用程序。

2 應用實例

選取某B0-B0軸式機車車輛幾何曲線通過計算主要技術參數，見表1。利用MATLAB 求解車鉤轉角和最小曲線半徑。

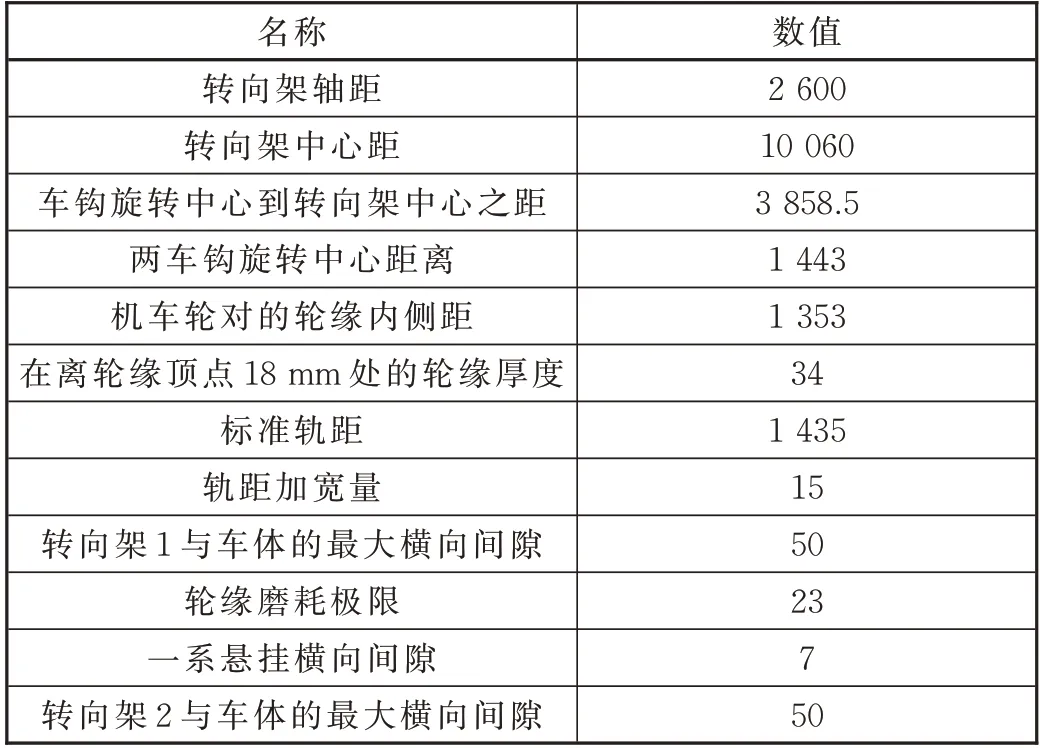
表1 機車幾何曲線通過主要技術參數 單位：mm

2.1 計算工況

工況1：曲線半徑為200 m。

工況2：曲線半徑為250 m。

工況3：曲線半徑為200 m，最大允許車鉤轉角γ1max=6°。

工況4：曲線半徑為250 m，最大允許車鉤轉角γ1max=6°。

2.2 計算結果

將表1 技術參數輸入到GUI 界面上模式1 和模式2，計算各工況下的車鉤轉角以及求已知最大的一車鉤轉角情況下的輪對橫動量和另一車鉤轉角。B0-B0軸式機車幾何曲線通過計算結果見表2，并生成圖4、圖5。

表2 計算結果

機車車輛通過曲線半徑200、250 m 時得到的車鉤轉角示意圖，如圖4、圖5 所示。為了驗證用MATLAB 編程來計算車鉤轉角的可靠性，利用CAD 繪圖軟件通過幾何繪圖法分別繪制出了過曲線半徑200、250 m 時的車鉤轉角并進行測量，如圖6、圖7 所示。當橫動量為82.5 mm，機車通過幾何曲線半徑為200、250 m 時，車鉤轉角分別為13°和10°，14°和9°。通過2 種方法的計算結果對比發現，曲線半徑為200 m 時，誤差相對較大，曲線半徑為250 m 時，計算結果基本一致。因為CAD 繪圖時，將車體長度、轉向架長度和車鉤長度的橫向投影距離默認為實際長度距離，存在著誤差，造成曲線半徑越小，誤差越大。而軟件程序計算依據公式法完成，公式在前期假設了一些理想條件，也會對程序計算結果造成一定誤差。無論是繪圖法的誤差或者程序化的誤差，都在允許的范圍內，不影響機車車輛設計分析需要。

圖4 過曲線半徑200 m 時的車鉤轉角

圖5 過曲線半徑250 m 時的車鉤轉角

圖6 過曲線半徑200 m 時的車鉤轉角（CAD 作圖）

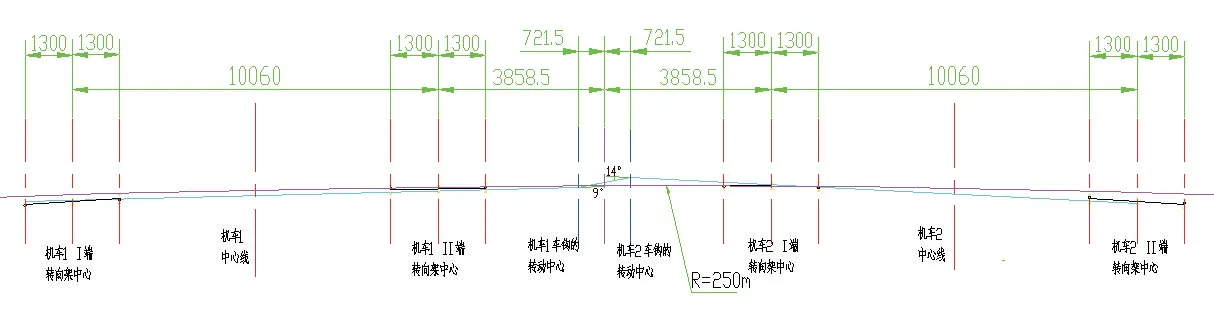
圖7 過曲線半徑250 m 時的車鉤轉角（CAD 作圖）

當假設轉向架構造上允許的最大轉角為θ′=2°，在GUI 界面輸入運行參數求得該車型通過的最小半徑為109.242 4 m，示意圖結果如圖8 所示。為了更直觀的了解它們的關系，通過MATLAB 畫出轉向架構造上允許的最大轉角和最小曲線圓半徑的關系圖，如圖9 所示。從圖9 中可以看出，最小曲線圓半徑受轉向架構造上允許的最大轉角影響很大。因此，合理確定轉向架構造上允許的最大轉角是確定最小曲線圓半徑的關鍵。

圖8 機車通過最小半徑示意圖

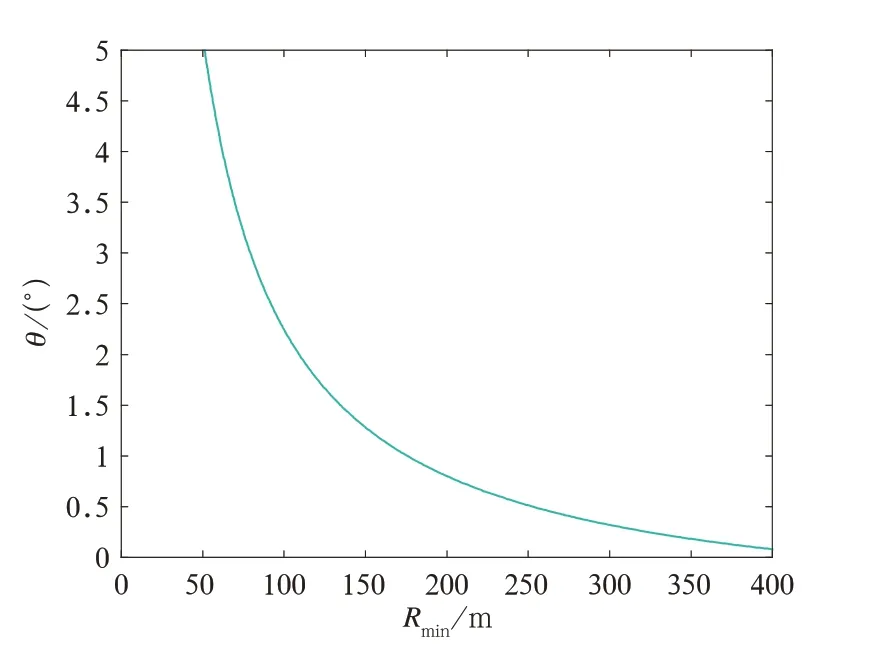
圖9 轉向架構造上允許的最大轉角和最小曲線半徑關系

3 結 論

文中利用MATLAB 設計出一種非常簡明、直觀的操作方式來解決目前計算幾何曲線通過存在問題，采取計算機結合編程來處理數據，將現有的幾何曲線通過計算程序化，盡可能地挖掘出數據所包的各種有用信息。

運用GUI 圖形界面，降低團隊其他成員對計算機語言的要求，進而提高了工作效率。通過程序畫出的示意圖，能直白地表達出所求參數。計算程序化的開發對企業的設計能力和影響力的提升有重要意義。

生成獨立的可執行的.exe 程序文件，可以在未安裝MATLAB 程序的電腦直接執行，使其使用范圍更廣，實用性更強。

本研究主要針對計算車鉤轉角和最小曲線半徑，而幾何曲線通過要解決的問題遠不止這些，因此下一步還需要不斷地完善和改進，并不斷擴充其功能。