爬壁機(jī)器人系統(tǒng)的廣義Lagrange方程

陸曉丹，張港

（1.浙江理工大學(xué)理學(xué)院，杭州 310018；2.浙江同濟(jì)科技職業(yè)學(xué)院，杭州 311231）

0 引言

爬壁機(jī)器人可以協(xié)助人們?cè)趶?fù)雜危險(xiǎn)的環(huán)境中進(jìn)行工作，應(yīng)用領(lǐng)域十分廣泛，因此在材料學(xué)、力學(xué)、物理學(xué)、數(shù)學(xué)、生物學(xué)、現(xiàn)代科學(xué)和工程技術(shù)領(lǐng)域等受到廣泛關(guān)注。研制爬壁機(jī)器人有兩個(gè)最需要考慮的因素：一個(gè)是爬壁機(jī)器人的移動(dòng)方式；另一個(gè)是爬壁機(jī)器人的吸附方式[1]。從爬壁機(jī)器人的吸附方式上來(lái)說(shuō)，主要可以分為真空吸附、磁吸附、仿生吸附、背推式吸附[2-5]。本文主要從運(yùn)動(dòng)機(jī)能上研究爬壁機(jī)器人。根據(jù)移動(dòng)方式的不同，爬壁機(jī)器人主要分為輪式、履帶式和足式[6]。各種移動(dòng)方式的對(duì)比如表1所示。

表1 不同移動(dòng)方式對(duì)比

未來(lái)爬壁機(jī)器人的研制將朝著靈活性高、體型小、操作智能化等方向發(fā)展。目前，輪式和履帶式爬壁機(jī)器人已經(jīng)得到廣泛應(yīng)用，而四足式仿壁虎型爬壁機(jī)器人具有得天獨(dú)厚的優(yōu)勢(shì)，從而在實(shí)際的應(yīng)用中能得到更為廣闊的發(fā)展[7]，因此本文以美國(guó)斯坦福大學(xué)研制的四足式仿壁虎型StickyBot III爬壁機(jī)器人[8]（如圖1）為研究對(duì)象。

圖1 StickyBotIII爬壁機(jī)器人

爬壁機(jī)器人系統(tǒng)動(dòng)力學(xué)模型的建立，有助于分析爬壁機(jī)器人的性能，設(shè)計(jì)控制算法及評(píng)估機(jī)器人移動(dòng)位置所需要的關(guān)節(jié)力矩等，可以為未來(lái)爬壁機(jī)器人的動(dòng)態(tài)優(yōu)化、控制算法、智能化和路徑規(guī)劃等提供強(qiáng)有力的理論支撐[9]。建立動(dòng)力學(xué)方程的方法有很多種，許多國(guó)內(nèi)外學(xué)者對(duì)不同類(lèi)型的爬壁機(jī)器人采用多樣的方法進(jìn)行動(dòng)力學(xué)分析并得到相應(yīng)的動(dòng)力學(xué)方程，在此做一些簡(jiǎn)單介紹。Xu等[10]利用牛頓力學(xué)的方法建立了輪式爬壁機(jī)器人系統(tǒng)的動(dòng)力學(xué)方程，分別對(duì)系統(tǒng)處于光滑面和越障兩種不同狀態(tài)進(jìn)行受力分析，建立了越障過(guò)程中系統(tǒng)的車(chē)輪和機(jī)身動(dòng)力學(xué)方程；岳榮剛等[11]以City-Climber履帶式爬壁機(jī)器人為原型，利用牛頓力學(xué)的方法，建立了該機(jī)器人在地面、垂直墻壁和天花板不同環(huán)境下的動(dòng)力學(xué)方程，該方程的建立為City-Climber機(jī)器人的路徑規(guī)劃和避障問(wèn)題提供了良好的解決方案，但上述兩個(gè)建模過(guò)程都較為復(fù)雜。徐亞茹等[12-13]利用U-K方程建立了輪式爬壁機(jī)器人的解析動(dòng)力學(xué)方程。事實(shí)上，利用U-K方程進(jìn)行建模需先利用Lagrange力學(xué)法建立系統(tǒng)在未受約束情況下的動(dòng)力學(xué)方程[14]，進(jìn)而利用U-K方程建立該系統(tǒng)的動(dòng)力學(xué)方程；并且徐在建模過(guò)程中并未考慮輪子與壁面之間摩擦力和輪子的轉(zhuǎn)動(dòng)慣量，但在實(shí)際情況中，這兩個(gè)是必須考慮的因素，因此本文將該因素考慮其中，以增強(qiáng)模型的適應(yīng)性。此外還有學(xué)者利用D-H法、牛頓-歐拉法等[15-18]建立了爬壁機(jī)器人系統(tǒng)的動(dòng)力學(xué)方程。

以上幾個(gè)典例是構(gòu)建爬壁機(jī)器人系統(tǒng)動(dòng)力學(xué)方程的幾種常見(jiàn)的方法，但可以看到，其過(guò)程都較為復(fù)雜，且爬壁機(jī)器人系統(tǒng)是一個(gè)復(fù)雜的多體約束力學(xué)系統(tǒng)，利用牛頓力學(xué)法對(duì)其受力分析時(shí)也較容易出錯(cuò)。本文利用Lagrange力學(xué)分析法，將爬壁機(jī)器人看作一個(gè)系統(tǒng)，選用廣義坐標(biāo)，計(jì)算該系統(tǒng)的動(dòng)能和勢(shì)能，定義系統(tǒng)的Lagrange函數(shù)，寫(xiě)出系統(tǒng)的非完整約束方程，并計(jì)算系統(tǒng)受到的外力和耗散函數(shù)，最后給出爬壁機(jī)器人系統(tǒng)的廣義Lagrange方程。

1 爬壁機(jī)器人的動(dòng)力學(xué)分析

1.1 爬壁機(jī)器人四肢動(dòng)力學(xué)分析

首先計(jì)算爬壁機(jī)器人系統(tǒng)四肢相對(duì)于身體的坐標(biāo)和速度。

根據(jù)爬壁機(jī)器人的肢體形態(tài)特點(diǎn)，考慮爬壁機(jī)器人的運(yùn)動(dòng)形態(tài)，為簡(jiǎn)化起見(jiàn)，將爬壁機(jī)器人系統(tǒng)四肢各關(guān)節(jié)看成是1個(gè)自由度的轉(zhuǎn)動(dòng)關(guān)節(jié)，并將爬壁機(jī)器人的單支腿簡(jiǎn)化為如圖2所示，簡(jiǎn)化結(jié)構(gòu)由身體0、股骨1、脛骨2和腳掌3組成。

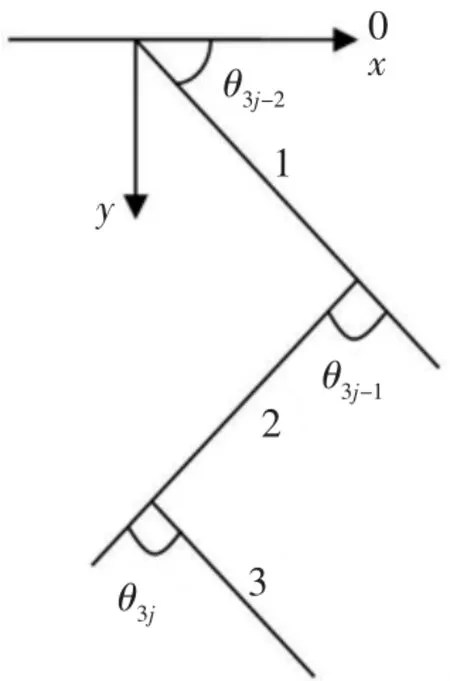
圖2 單肢結(jié)構(gòu)簡(jiǎn)圖

其中構(gòu)件1和構(gòu)件0的連接處為髖關(guān)節(jié)，構(gòu)件1和構(gòu)件2的連接處為膝關(guān)節(jié)，構(gòu)件2和構(gòu)件3的連接處為踝關(guān)節(jié)。定義θ3j-1、θ3j-2、θ3j等四肢各關(guān)節(jié)的傾斜角度（其中j為爬壁機(jī)器人四肢的數(shù)量）。為方便起見(jiàn)，假設(shè)爬壁機(jī)器人系統(tǒng)四肢各關(guān)節(jié)長(zhǎng)度相等為l，質(zhì)量相等為m′，同時(shí)引入qi=θi（i=1，2，…，15）作為廣義坐標(biāo)，并用廣義坐標(biāo)表示直角坐標(biāo)。

那么，爬壁機(jī)器人的股骨相對(duì)于身體的質(zhì)心坐標(biāo)可用廣義坐標(biāo)表示為：

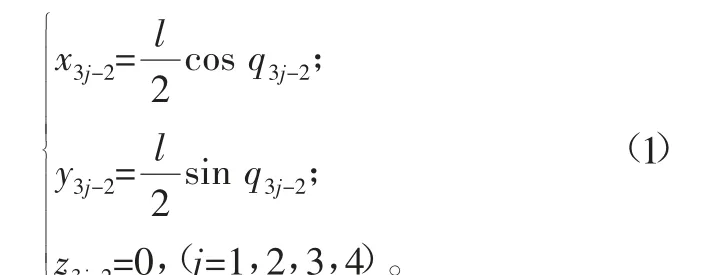
脛骨相對(duì)于身體的質(zhì)心坐標(biāo)可用廣義坐標(biāo)表示為：

1.2 爬壁機(jī)器人機(jī)身動(dòng)力學(xué)分析

接下來(lái)研究運(yùn)動(dòng)過(guò)程中爬壁機(jī)器人機(jī)身中心位置坐標(biāo)及速度變化。

爬壁機(jī)器人的工作環(huán)境一般為豎直的平面、圓柱面和圓錐面等，本文基于圓錐壁面的工作環(huán)境下討論，因?yàn)閳A錐壁面較其他壁面復(fù)雜，所以只要解決了爬壁機(jī)器人在圓錐壁面上的運(yùn)動(dòng)學(xué)原理，那么在其余工作環(huán)境下的運(yùn)動(dòng)學(xué)問(wèn)題也就迎刃而解。現(xiàn)將爬壁機(jī)器人的工作壁面的圖形簡(jiǎn)要畫(huà)出（如圖3）。

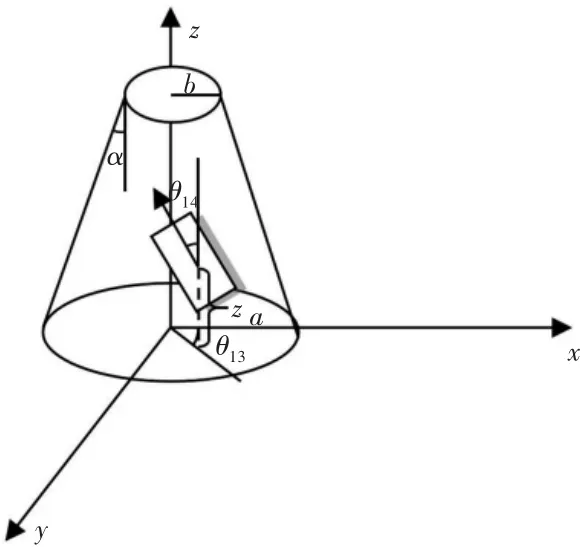
圖3 爬壁機(jī)器人工作壁面簡(jiǎn)圖

在地面中心創(chuàng)建一個(gè)固定的笛卡爾坐標(biāo)系{x，y，z}，則在圓錐壁面工作環(huán)境下，爬壁機(jī)器人的質(zhì)心位置根據(jù)幾何學(xué)可用下面的公式表示：

1.3 爬壁機(jī)器人系統(tǒng)動(dòng)力學(xué)分析

設(shè)爬壁機(jī)器人在攀爬過(guò)程中不發(fā)生側(cè)滑，只存在靜摩擦，可以得到非完整約束條件為

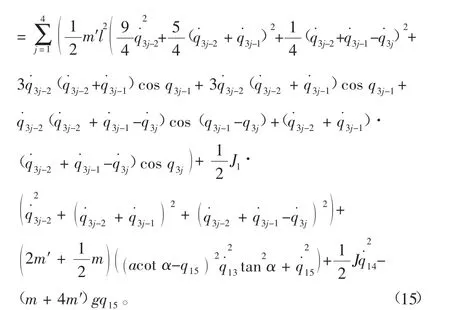
2 爬壁機(jī)器人系統(tǒng)的運(yùn)動(dòng)微分方程

2.1 爬壁機(jī)器人系統(tǒng)的Routh方程

采用Lagrange乘子法，得到非完整爬壁機(jī)器人系統(tǒng)的運(yùn)動(dòng)微分方程，即Routh方程為：

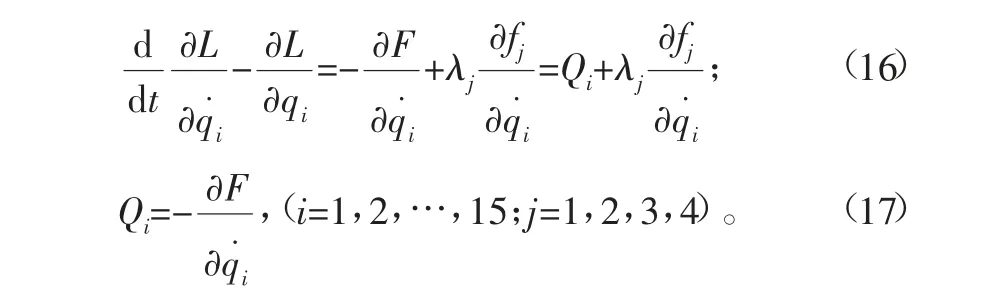
式中：Qi=Qi（t，q，q˙）為非完整爬壁機(jī)器人系統(tǒng)的非勢(shì)廣義力；F為爬壁機(jī)器人4條腿各關(guān)節(jié)之間的摩擦耗散函數(shù)，假設(shè)爬壁機(jī)器人系統(tǒng)腳掌與地面之間的平動(dòng)和轉(zhuǎn)動(dòng)的摩擦因數(shù)分別為μ1和μ2，因此爬壁機(jī)器人系統(tǒng)的摩擦耗散函數(shù)為

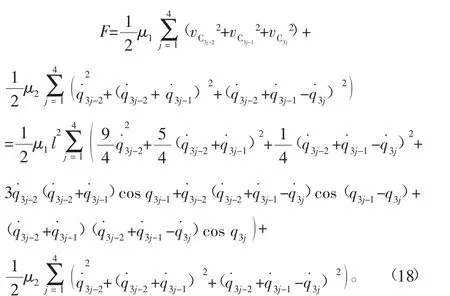
其中，vc3j-2、vc3j-1、vc3j分別為爬壁機(jī)器人系統(tǒng)中四肢各關(guān)節(jié)中心位置的速度。

2.2 爬壁機(jī)器人系統(tǒng)的Lagrange方程

設(shè)系統(tǒng)（16）非奇異，即det（?2L/?q˙s?q˙k）≠0（s，k=1，2，…，15），則由式（10）和式（16）可求出所有λj=λj（t，q，q˙），（j=1，2，3，4），式（16）便可寫(xiě)為

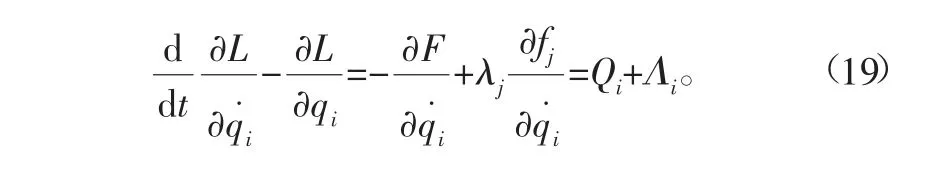
式中：

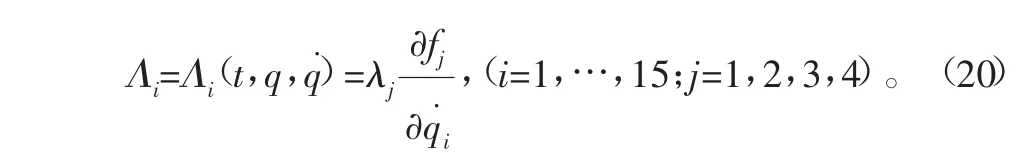
式中，Λi為廣義約束反力。

式（19）為非完整爬壁機(jī)器人系統(tǒng)方程式（10）和式（16）相應(yīng)的完整系統(tǒng)的運(yùn)動(dòng)微分方程，即Lagrange方程。

3 爬壁機(jī)器人系統(tǒng)的廣義Lagrange算例

通過(guò)以上討論，已經(jīng)得出非完整爬壁機(jī)器人系統(tǒng)在圓錐壁面上的Lagrange函數(shù)及非完整爬壁機(jī)器人系統(tǒng)Routh方程式（16）和相應(yīng)完整系統(tǒng)的Lagrange方程式（19）。現(xiàn)給出圓錐壁面上具體的廣義Lagrange方程。將式（10）、式（15）、式（18）代入式（16）得：

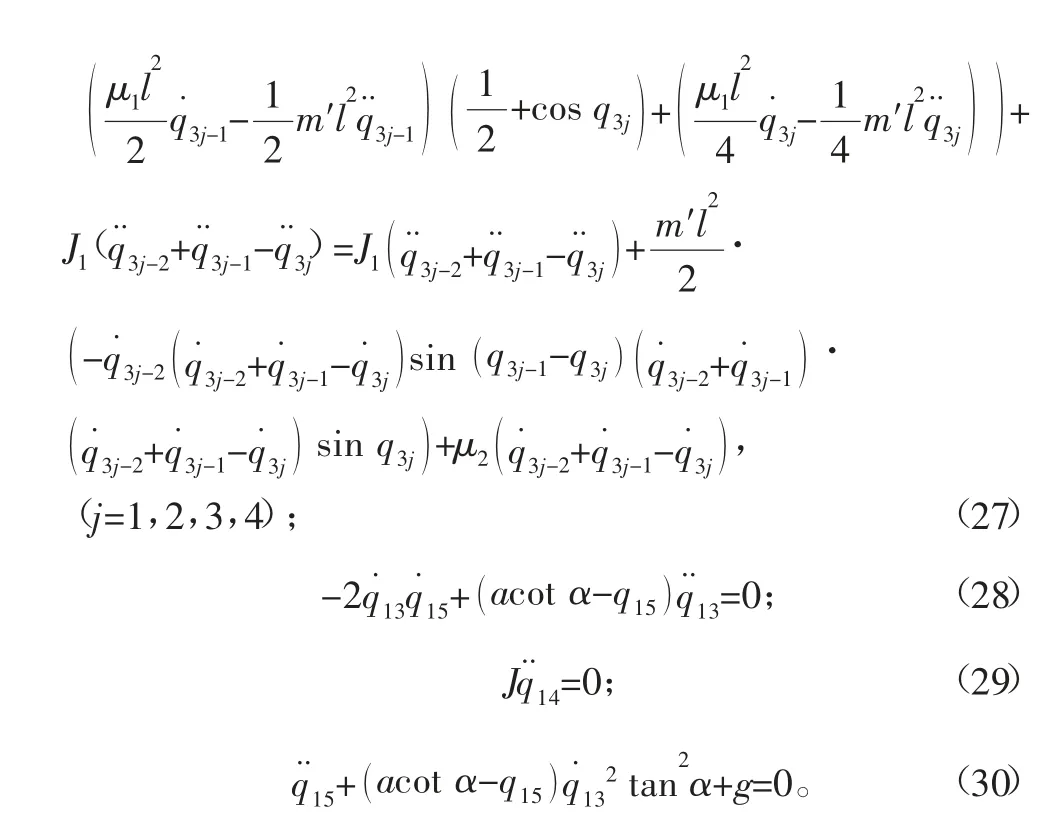
4 結(jié)論

本文將Lagrange力學(xué)法引入到四足式爬壁機(jī)器人系統(tǒng)，根據(jù)爬壁機(jī)器人系統(tǒng)運(yùn)動(dòng)過(guò)程分析了爬壁機(jī)器人系統(tǒng)的動(dòng)能、勢(shì)能及所受的非完整約束，給出爬壁機(jī)器人系統(tǒng)的Lagrange函數(shù)并建立了該系統(tǒng)廣義Lagrange方程。在最后給出爬壁機(jī)器人系統(tǒng)廣義Lagrange算例，求出在圓錐壁面上非完整爬壁機(jī)器人的Lagrange乘子（24），得到非完整爬壁機(jī)器人系統(tǒng)相應(yīng)完整爬壁機(jī)器人系統(tǒng)的運(yùn)動(dòng)微分方程即Lagrange方程。利用Lagrange力學(xué)方法研究四足式爬壁機(jī)器人系統(tǒng)更為簡(jiǎn)便，形式上也具有較高的統(tǒng)一性。

在本文取得成果的基礎(chǔ)上，可以引入Lie群分析法，建立該系統(tǒng)的對(duì)稱(chēng)性理論，得到相應(yīng)守恒量，從而得出爬壁機(jī)器人系統(tǒng)的運(yùn)動(dòng)規(guī)律。