高超聲速飛行器無在線求導backstepping控制方法

路 遙，賈志強，劉曉東，路坤鋒

(1.宇航智能控制技術國家級重點實驗室，北京 100854；2.北京航天自動控制研究所，北京 100854)

0 引 言

高超聲速飛行器(Hypersonic vehicle, HSV)是指飛行馬赫數大于5的飛行器，因其巨大的軍民應用前景而受到各航天強國的關注。由于HSV模型具有非線性程度高、含有不確定未知項以及參數不確定等特點，為HSV設計飛行控制器非常具有挑戰性。許多學者基于非線性控制方法研究HSV的控制器設計問題，并取得了良好的控制效果。

Backstepping是一種常用的非線性控制設計工具，尤其適合于具有嚴反饋形式的非線性系統。由于HSV縱向通道非線性模型可以在一定的合理假設下簡化為嚴反饋形式，因此很多學者基于backstepping方法設計HSV飛行控制器。文獻[6]在backstepping方法的基礎上設計了事件觸發機制的自適應神經網絡控制器。文獻[7]基于backstepping方法設計了一種容錯量化控制器。文獻[8]考慮了HSV實際飛行過程中航跡傾角和攻角測量精度低的問題,設計了一種有限時間收斂自適應模糊非光滑backstepping控制器。文獻[9-10]針對一類考慮模型非仿射特性和執行機構飽和的HSV軌跡跟蹤控制問題,提出了一種基于backstepping的輸出反饋控制方法。文獻[11]針對非最小相位HSV模型，提出一種基于backstepping的魯棒自適應神經網絡控制方法。文獻[12]針對高超聲速飛行器同時存在多源干擾和執行機構故障的問題,提出一種自適應容錯backstepping控制策略。

以上基于backstepping的控制方法均取得了良好的控制效果，但控制結構均比較復雜,這主要是由于現有backstepping方法在應用中需要解決求取虛擬控制量一階導數時存在的“復雜性爆炸”問題。學者通常采用在線估計的方法獲取虛擬控制量一階導數的近似值用以構建控制律，常見的方法有動態面法、指令濾波法、跟蹤微分器法、神經網絡逼近法等。然而，無論采用何種方法，均需構建若干環節處理“復雜性爆炸”問題，這便導致控制器結構更加復雜，需要調整和設計的控制參數增多，加大了設計難度。另一方面，對虛擬控制量一階導數進行估計必然會產生一定的估計誤差，這也會影響控制器的控制效果，降低預期的控制品質。

針對上述問題，本文針對HSV縱向通道的跟蹤控制問題，提出一種新型的不需進行虛擬控制量在線求導的backstepping控制方法以實現對航跡傾角參考軌跡的穩定跟蹤。通過引入一個高階微分器構建不確定項估計器，直接構建虛擬控制量一階導數的控制律，從而避免了對虛擬控制量進行在線求導環節。基于Lyapunov方法證明了閉環系統的穩定性，并通過仿真對比實驗驗證所提方法的有效性。

1 HSV縱向通道非線性模型

以文獻[14]中提出的一類HSV作為研究對象，其進行巡航飛行時縱向通道剛體非線性動力學模型可描述為：

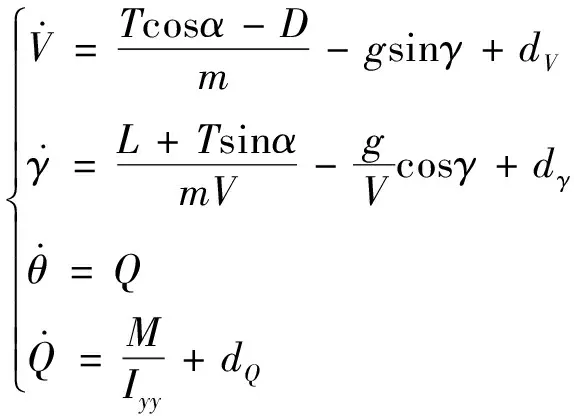
(1)

其中，,,,分別表示飛行器的速度、航跡傾角、俯仰角和俯仰角速度；表示攻角，可按=-計算；,,分別表示質量、重力加速度和俯仰通道轉動慣量；,,表示因外部環境干擾和氣動/推進耦合因素引起的模型不確定項；,,,分別表示推力、阻力、升力和俯仰力矩；基于文獻[14]的分析結果，忽略升降舵偏角對阻力的影響，并使用鴨翼與升降舵聯動消除舵偏角對升力的耦合作用后，氣動力和氣動力矩的計算公式如下所示：

(2)

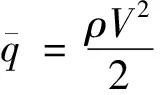
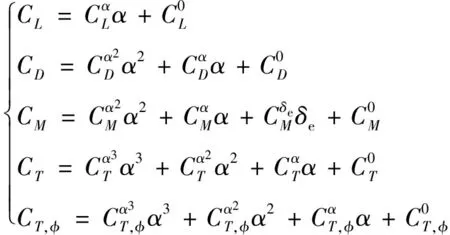
(3)

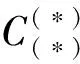
2 無虛擬控制在線求導backstepping控制器設計

2.1 問題描述

控制器設計的目標為保證飛行器的速度和航跡傾角狀態分別穩定跟蹤預先設定的連續光滑的參考軌跡和。為實現此目標，首先將飛行器模型分為速度子系統和航跡傾角子系統兩個部分。

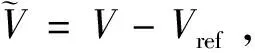
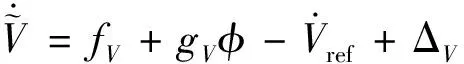
(4)

其中，

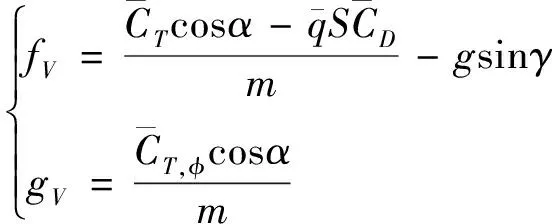
(5)

Δ為由推力/氣動系數偏差引起的不確定項和不確定項組成的總不確定項。速度子系統通過進行控制。

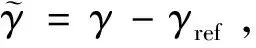
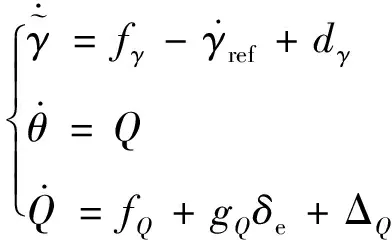
(6)

式中，

(7)

Δ為由推力/氣動系數偏差引起的不確定項和不確定項組成的總干擾項。航跡傾角子系統通過進行控制。

在進行具體控制器設計前，首先給出如下假設：

模型不確定項,,的一階導數存在。

模型不確定項,,是由風干擾、大氣密度偏差、發動機尾噴管噴出的高溫高速氣流導致后體膨脹引起的額外力矩組成，在實際中均是連續光滑變化的，因此假設1是合理的。

2.2 速度子系統控制器設計

為估計式(4)中的未知總干擾項Δ，首先引入文獻[15]中提出的跟蹤微分器估計速度的一階導數：

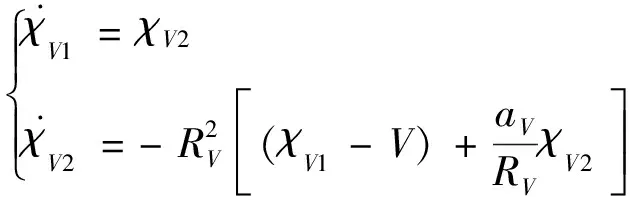
(8)

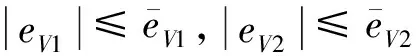
(9)

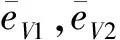
基于式(8)設計如下干擾觀測器

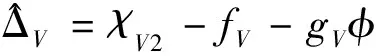
(10)

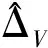
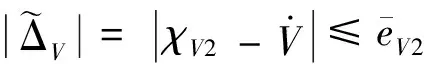
(11)

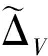
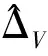
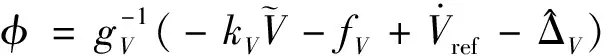
(12)

其中，>0為待設計的常值控制增益。

2.3 航跡傾角子系統控制器設計

航跡傾角子系統控制器基于backstepping方法設計。與現有backstepping方法設計流程不同，本文提出一種無需進行虛擬控制指令求導的backstepping設計策略，以避免現有設計流程中求解虛擬控制指令導數時的“復雜性爆炸”問題。

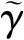
(13)

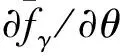
根據文獻[14,16]中不同HSV模型的數據，可驗證在各種合理的推力/氣動小導數偏差組合下，假設2均是成立的；且假設2的物理含義已在文獻[16]中詳述，因此假設2是合理的。

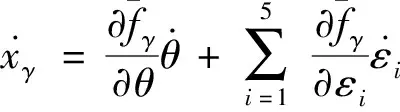
(14)

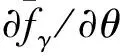
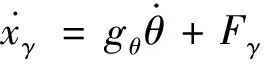
(15)

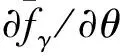
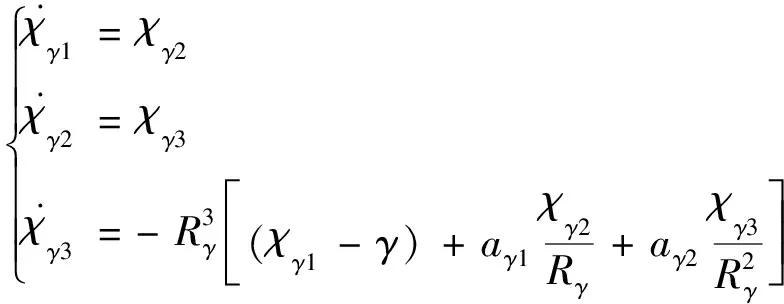
(16)

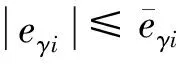
(17)

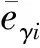
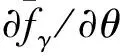
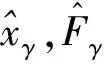
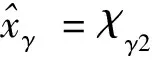
(18)

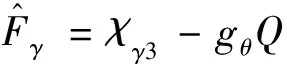
(19)

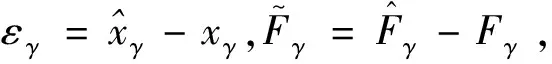
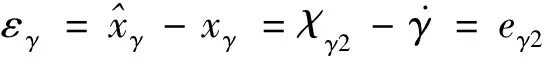
(20)

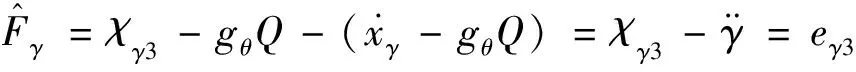
(21)

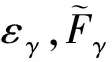
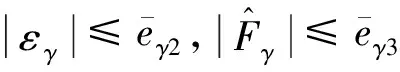
(22)

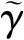
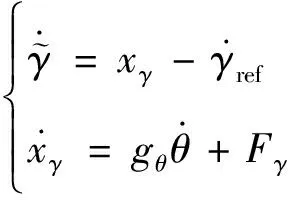
(23)

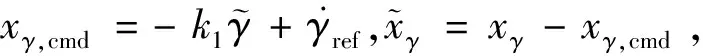
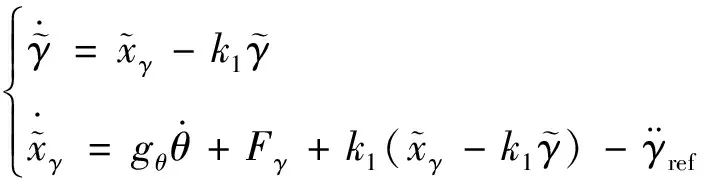
(24)

設計虛擬控制量的控制律為

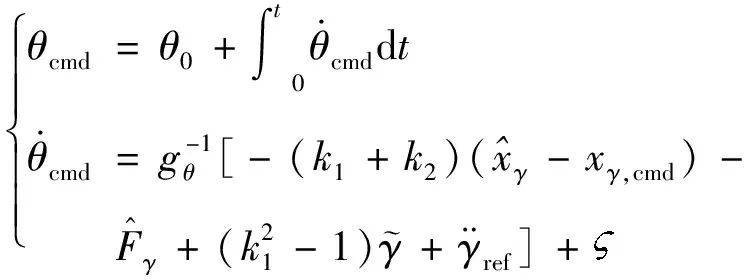
(25)

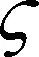
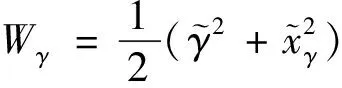
(26)

結合式(23)和(24)，對其求導可得

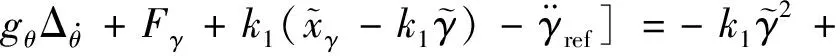
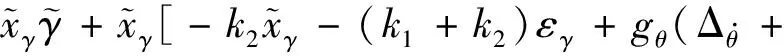
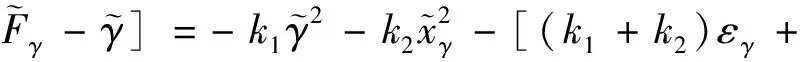
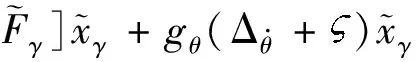
(27)

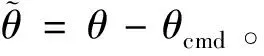
(28)

以作為本步中的虛擬控制量，設計如下虛擬控制律

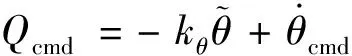
(29)

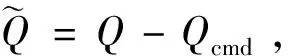
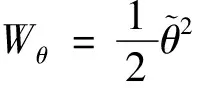
(30)

對其求導可得

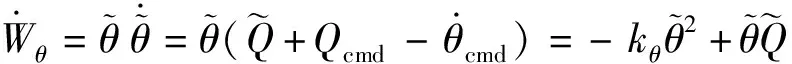
(31)

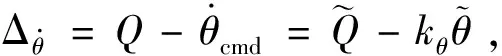
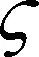
(32)

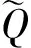
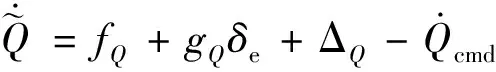
(33)

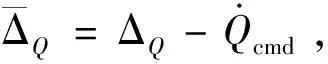
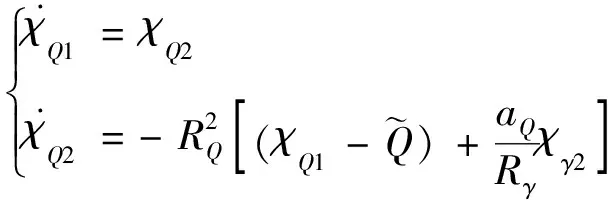
(34)

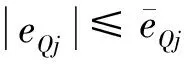
(35)

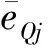
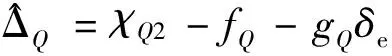
(36)

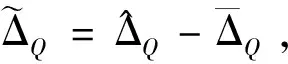
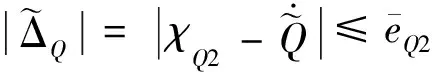
(37)

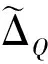
注意到在合理飛行狀態下≠0，設計的控制律為

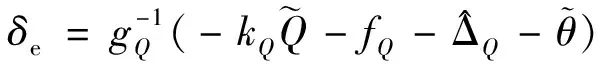
(38)

其中，>0為待設計增益常數。考慮候選Lyapunov函數

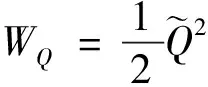
(39)

對其求導可得

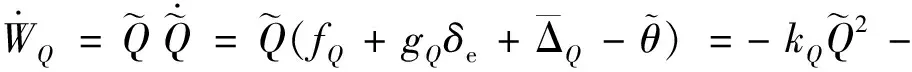
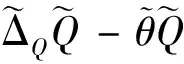
(40)

圖1給出了本文所設計的控制器的結構框圖。

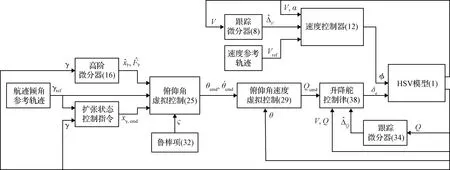
圖1 控制器結構框圖

3 穩定性分析

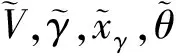
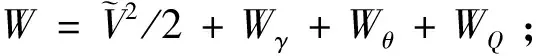
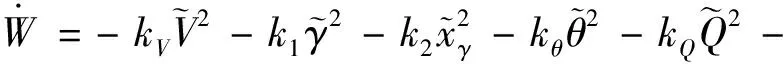
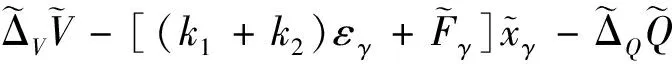
(41)

由式(11)、(22)和(37)進一步可得

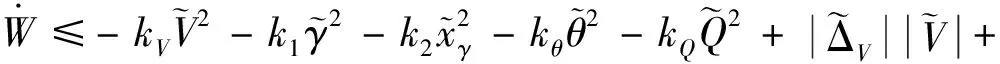
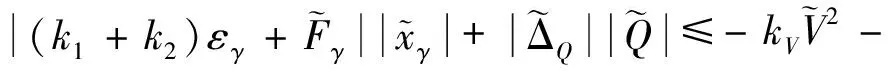
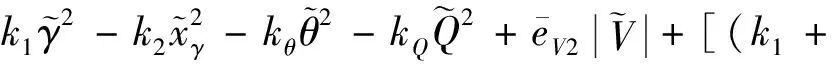
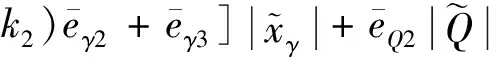
(42)

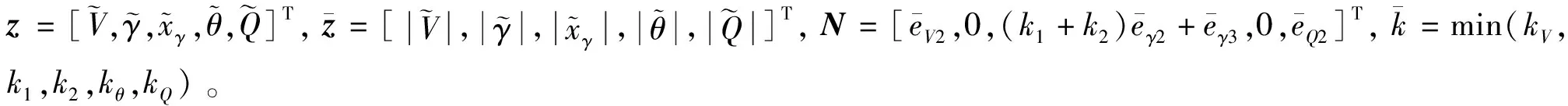
(43)

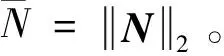
4 仿真校驗

本章通過仿真對比實驗驗證所設計控制方案的有效性。仿真模型基于式(1)-(3)建立。飛行器總體和氣動參數參見文獻[14]中的附表，其中氣動參數偏差取-20%。仿真狀態初值設置為

(44)

參考軌跡和設置為

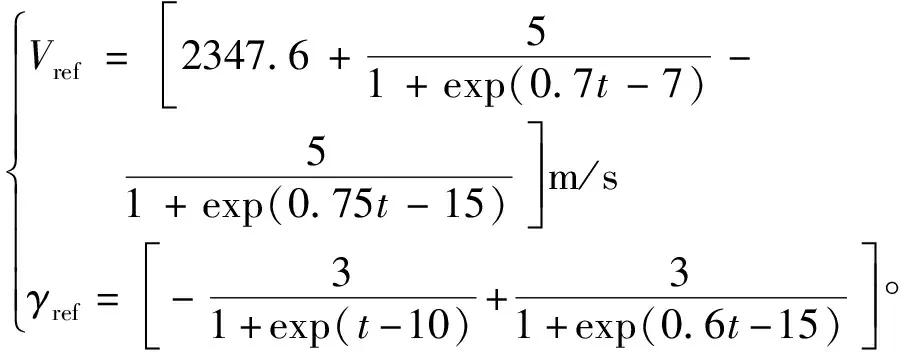
(45)

外部干擾,,設置為

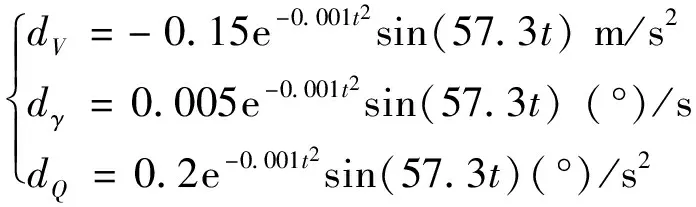
(46)

選取文獻[10]提出的backstepping控制方法作為對比方案。本文和對比方案的控制器參數設置見表1。

表1 控制器參數設置

為盡量保證仿真實驗的公平性，作者主要參考文獻[10]中提供的對比方法參數設置情況進行本次實驗控制增益的設置。

為更好地展示仿真對比效果，引入如下航跡傾角跟蹤誤差評價指標

(47)

對比仿真結果如圖2-9所示：

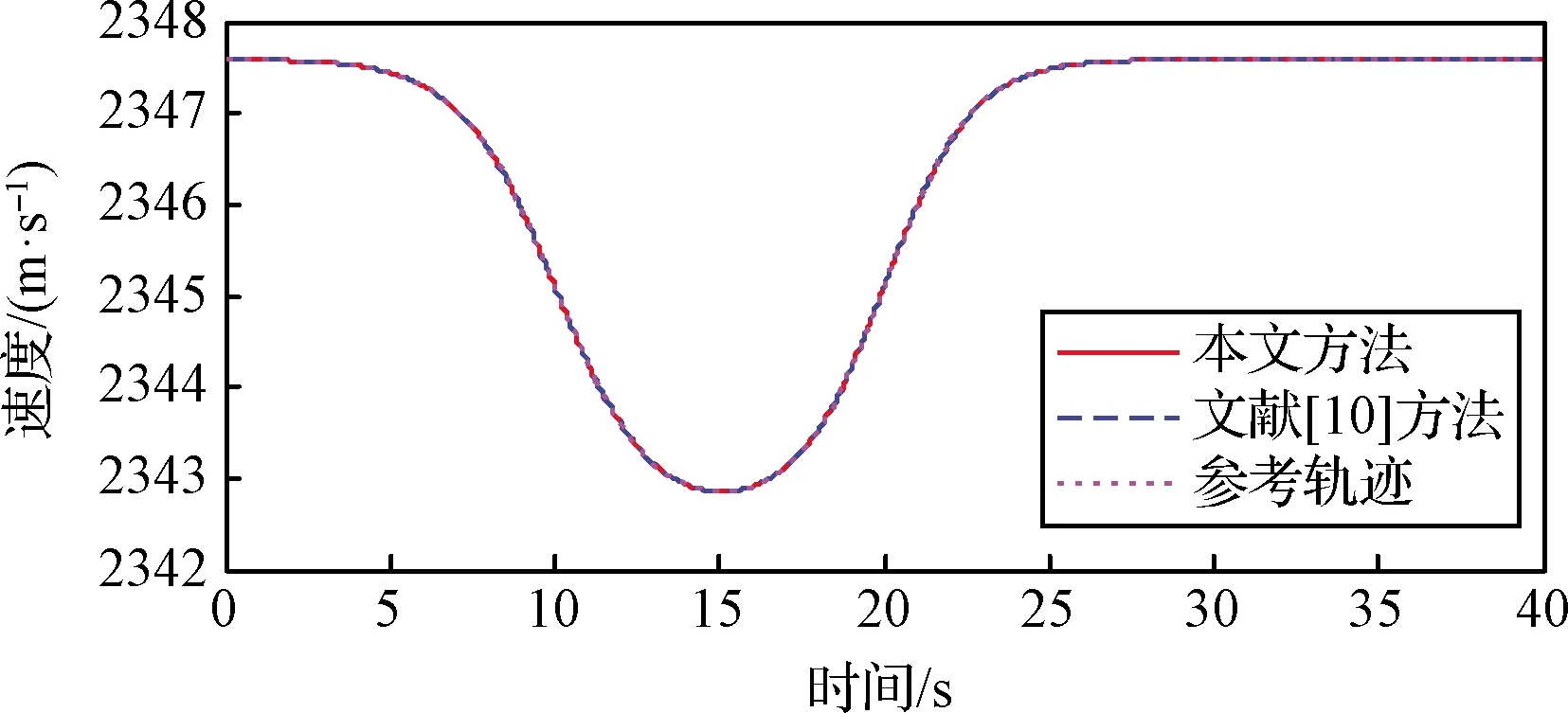
圖2 速度跟蹤曲線

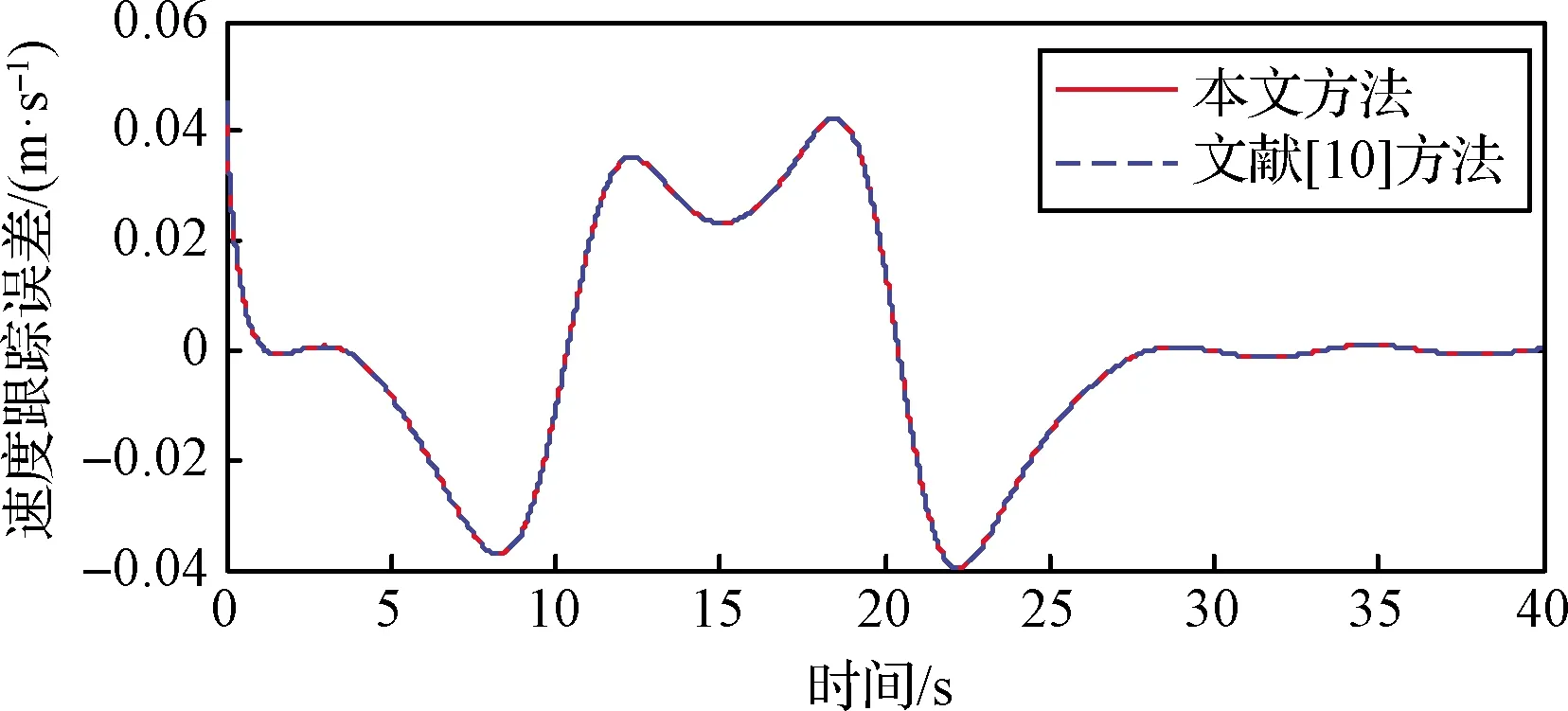
圖3 速度跟蹤誤差曲線

圖4 航跡傾角跟蹤曲線

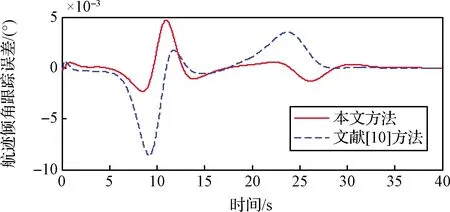
圖5 航跡傾角跟蹤誤差曲線

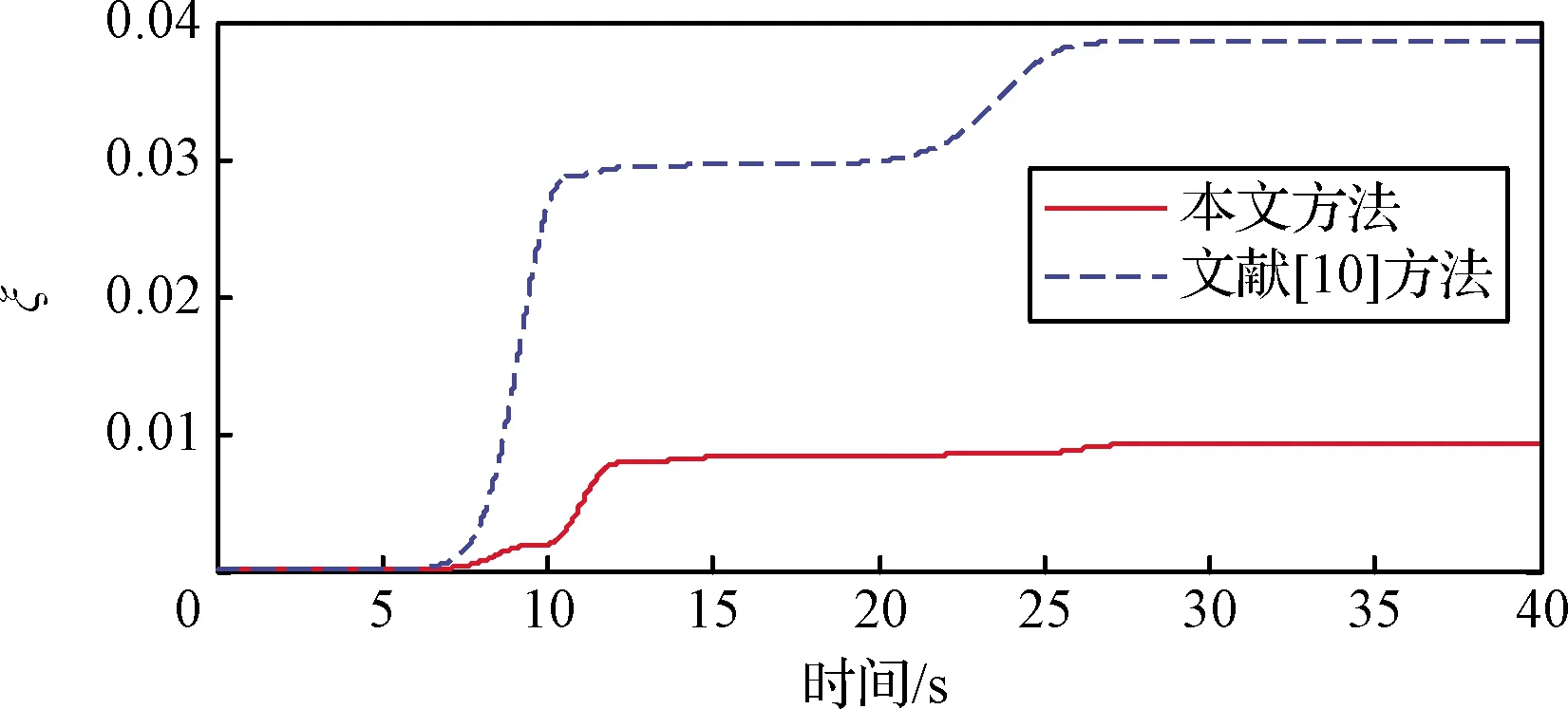
圖6 航跡傾角跟蹤誤差評價指標ξ

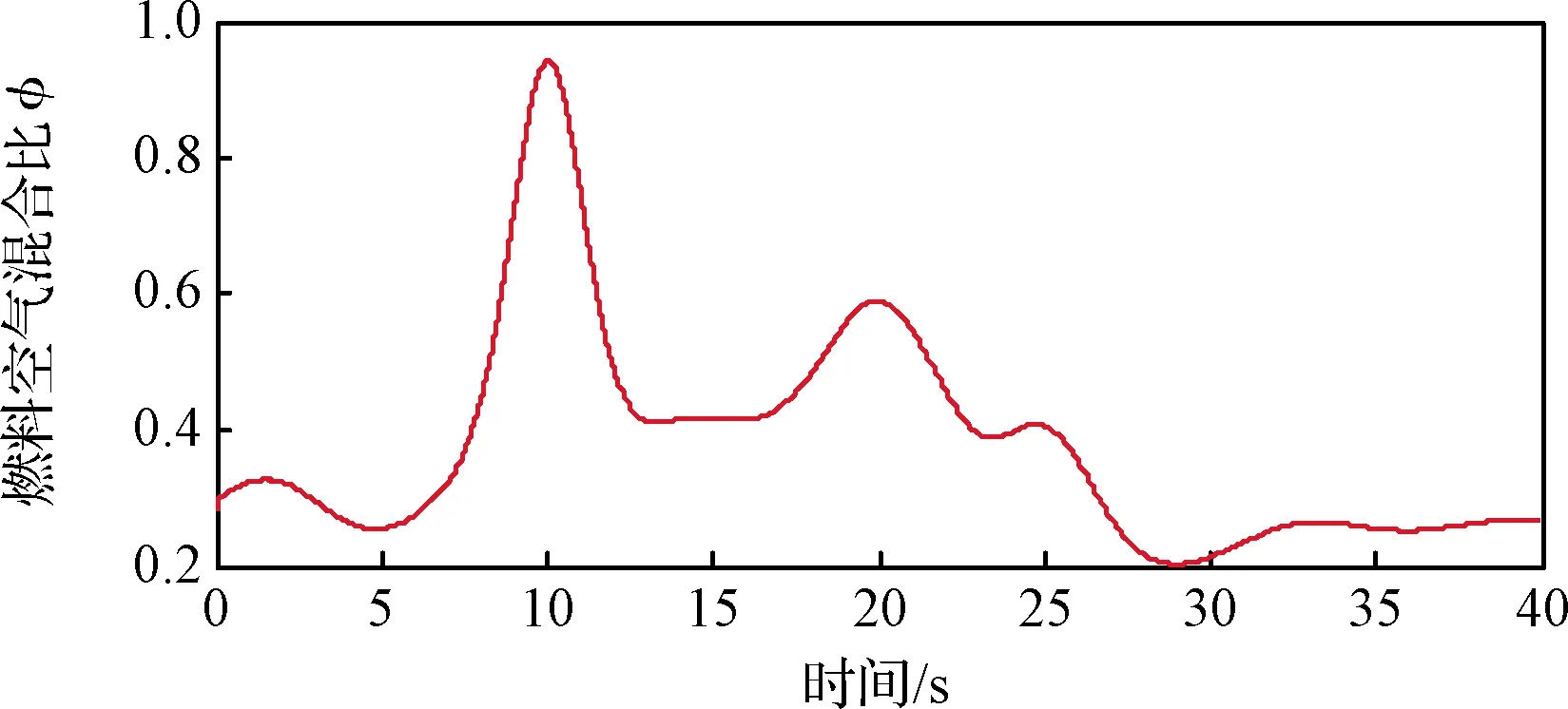
圖7 本文方法燃料空氣混合比φ

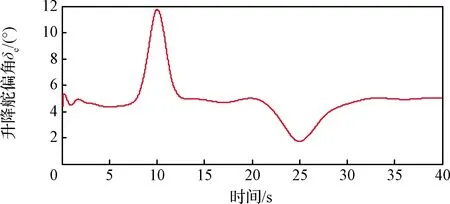
圖8 本文方法升降舵擺角δe

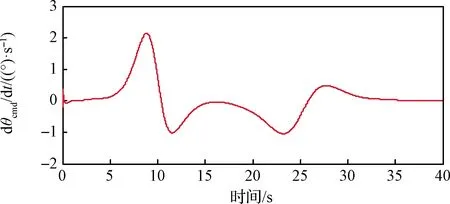
圖9 本文方法虛擬控制量dθcmd/dt

圖2和圖3分別給出了兩種方案的速度跟蹤對比曲線和速度跟蹤誤差對比曲線。可以看出兩種方案速度狀態的跟蹤情況相差很小，這是由于兩種方案的速度子系統采用了相同的控制律結構，且控制參數基本相同。圖4-6給出了航跡傾角跟蹤情況。由圖6所示的航跡傾角跟蹤誤差評價指標可以看出本文方法得到的明顯優于對比方法，這即證明了本文所提航跡傾角子系統控制方案相較現有backstepping控制方案的有效性和優越性。

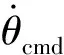
5 結 論

對于高超聲速飛行器縱向通道跟蹤控制問題，本文提出了一種改進的backstepping控制方案。相較于現有backstepping設計流程，本文所提方案直接設計了虛擬控制量一階導數的控制律，從而避免了現有backstepping方法應用時存在的“復雜性爆炸”問題；而且，本文方法控制器結構簡單，待設計控制器參數數目較少。對比仿真實例結果表明本文方法能夠保證閉環系統具有良好的跟蹤性能。