多區域分布式能源站選址及供能管線布局規劃研究

孟政吉,陳鑠鑫,胡雪凱,孟 良,周 昊

(1.國網河北省電力有限公司電力科學研究院,河北 石家莊 050021;2.河北華瑞能源集團有限公司,河北 石家莊 050021)

0 引言

當今世界,能源系統正在向著更清潔、更低碳、更高效的目標發展。2014年,習近平總書記提出“四個革命、一個合作”的重大能源戰略思想[1]。綜合能源是新型能源戰略的探索與實踐[2]。綜合能源系統(integrated energy system,IES)指通過各類能源耦合裝置將傳統分立的能源供應源、供應網絡、用戶互聯而形成的能源系統,可以看作能源互聯網的物理基礎。各能源形式相互耦合,協同運行,可增加系統中能源供給者與消費者之間的聯系,豐富能源系統規劃對象,深化能源系統運行調度方式,為不同能源間的互聯協調創造可能[3]。分布式能源站(distributed ener gy station,DES)是綜合能源系統多能源耦合的核心,也是代替集中供能,將多能源用戶融入綜合能源系統的重要載體,作為系統中用戶與能源網絡之間的連接節點,起到了非常重要的作用[4]。

目前,有關DES的規劃研究多集中于其內部集成設備的配置規劃,通過優化算法,確定能源站內部設備的種類、容量,而對于能源站建設位置的規劃研究較少[5]。實際上,確定能源站的位置以及能源供能管線路徑布局是保障系統經濟效益的關鍵。特別是對于包含多個DES的區域綜合能源系統,能源站與能源站間的距離及管道鋪設布局均與各能源站的位置息息相關。通過合理的規劃確定各個能源站的建設位置以及能源站-負荷間、能源站間的供能管線布局,有助于減少供能管網的建設成本,為后續能源站間互聯協調建立基礎,提升多區域綜合能源系統整體的經濟性[6]。

現有考慮能源站的選址規劃中,文獻[7]通過工程經濟學理論構建區域能源站與管網優化的數學模型,提出了能源站管道的工程敷設方式與管網規劃方法;文獻[8]研究了基于圖論最小生成樹理論的能源站選址與供能管道規劃方法。但文獻[7]和文獻[8]均只考慮了一種能源形式,不能適應綜合能源系統多能源的需要,并且規劃模型通過遍歷算法進行求解,效率相對較差。文獻[9-10]提出了能源站選址及供能管線布局規劃方法,但均假設各能源站供能管線的長度為能源站到負荷間的直線距離,未考慮區域能源條件、種類以及市政道路規劃對于管道布局的影響。現有綜合能源系統往往具有多座分布式能源站,將不同區域的能源站相互連接,可以實現能源站間的互聯互通與互補互濟,達到改善多區域系統整體的用能方式,提升系統經濟性的目的[3]。而多區域能源站相互連接,也需要首先確定各能源站的建設位置以及能源站間互聯管線的布局。

1 多區域分布式能源站選址規劃

1.1 多區域分布式能源站系統結構

DES的應用解決了區域多能負荷的能源供應問題,但不同區域往往由于資源稟賦與地塊功能的差異,存在不同的供用能需求。因此,針對多個區域僅建立一座DES,在一定程度上存在設備選型、定容困難,能源遠距離傳輸損耗過大等問題。因此,針對具備能源供應需求的多區域整體進行規劃,建設多座分布式能源站,并將不同區域的能源站相互連接,既可以對多區域負荷供能,又可以實現能源站間的互聯互通與互補互濟,達到“供能”與“協調”的雙重目的。多區域分布式能源站系統結構如圖1所示,不同區域負荷根據需求特性及供能經濟性由相應區域的能源站供能,不同能源站又通過互聯管線相互耦合成為一個整體,從而實現區域間能源的調度與協調。

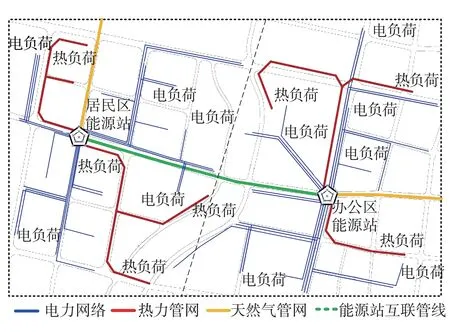
圖1 多區域分布式能源站系統示意

由圖1可以看出,根據區域資源稟賦與負荷的供用能需求,選擇合適的位置建設DES,并規劃電、氣、冷、熱等多能管線的鋪設布局,是建設區域綜合能源系統的基礎。同時,為了實現不同區域能源站的互聯與協調,也需要對能源站間互聯管線的布局進行規劃。由于能源在站間協調存在一定的損耗,能源站互聯管線的路徑長度將決定能源站互聯協調的經濟性。確定最優的互聯管線布局,對于多能源站互聯尤為重要。

1.2 多區域分布式能源站選址規劃模型

1.2.1 基于P-中值模型的能源站選址模型

一般情況下,能源站的選址問題可以抽象成為由“點”和“邊”構成的數學問題,并借助圖論的方法進行求解。其中,能源站和能源用戶就是各個網絡節點,輸送能源的管道或者線路就是網絡中的邊,從多個待選節點中選出一個或者P個節點,并由這些節點上的能源站與用戶相連實現能源供應,就屬于能源網絡中的P-中值問題[9]。通過P-中值模型進行選址的優勢在于,其所構建的模型多為線性優化模型,相比較非線性優化,線性優化模型具有求解速度和求解精度多方面的優勢,有助于修正規劃參數,快速得到規劃結果。

基于P-中值模型的能源站選址問題可以概括為:在平面S內共存在n個多能負荷節點,m個能源站候選位置節點。如何通過計算從m個候選位置節點中選擇P個合適的節點使得能源站為能源用戶供能的賦權距離之和最小,通過公式可以表示為:

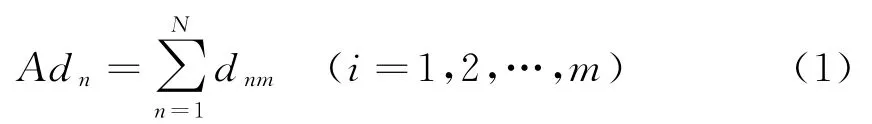
式中:n表示負荷節點個數;m為候選位置個數;為圖中負荷節點i到所有候選節點距離的總和;為2個節點n與m之間的最短距離。求解場景如圖2所示,其中n=7、m=4、P=2。

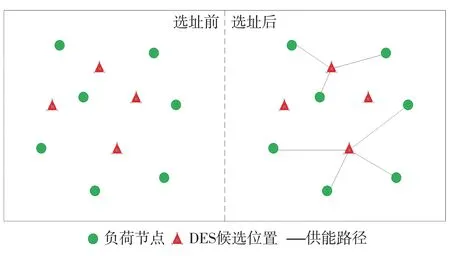
圖2 DES選址問題示意(n=7、m=4、P=2)

具體可以表示為

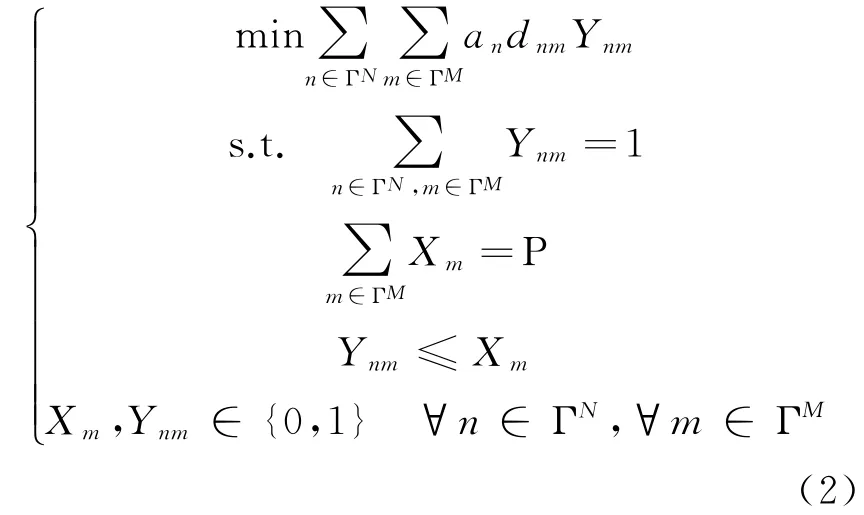
式中:ΓN為負荷的節點集合;ΓM為能源站待建位置的集合;an為節點n的能源需求量;dnm為負荷節點n至各能源站m的直線距離;Xm為待選位置是否被選中,若m節點被選中建設能源站,則其為1,否則為0;Ynm為負荷節點n是否通過能源站m供能,若是則其為1,否則為0。

1.2.2 適應多能源規劃的P-中值模型

可以看出,上述P-中值模型選址問題只能體現一種能源形式。但與單一能源系統規劃不同的是,綜合能源系統中的用戶存在多種能源利用形式,對于能源站的選址規劃還需要考慮到不同用戶對于能源需求的多樣性。因此,本文引入多能負荷需求系數an替代原模型能源需求量an,體現綜合能源系統負荷對于能源需求的多樣性。多能負荷需求系數an,計算公式可以表示為

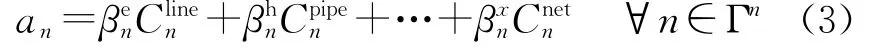
式中:βen為負荷節點n的電能需求系數;βhn為負荷節點n的熱能需求系數;βxn為負荷節點n其他能源形式的需求系數,需求系數若需要供應則為1,否則為0;Clinen為電力線路建設單位成本;Cpipen為熱力管道建設單位成本;Cnetn為其他形式的能源管線建設成本,可以通過擬合得到。

通過擬合得到電力線路單位長度建設成本與額定容量的關系

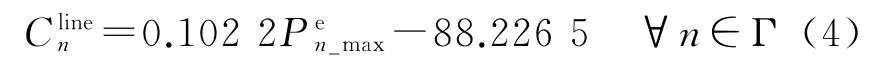
其中,為了滿足能源站對負荷節點的供能,電力線路的功率上限Pen_max表示為負荷節點n所需的最大電功率。

對于其他類型的能源種類,管線的傳輸能力上限可以根據需求選用流量、壓力等形式表示,這里不再贅述。但考慮到后續多能源站優化規劃往往需要將流量等參數轉化為功率表示,以熱力管線為例,其流量和功率可通過熱力網絡潮流求解公式進行轉化

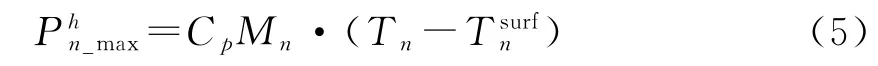
式中:Phn_max為負荷節點n所需的最大熱功率;Cp為管道傳輸介質的比熱容;Mn為節點n供熱管道p的水流量上限;Tn為管道p的工質水流溫度,一般規劃優化取95℃;Tsurfn為管道p外部土壤溫度,一般規劃優化取25℃。

基于此,通過擬合得熱力管道單位長度建設成本與額定容量的關系

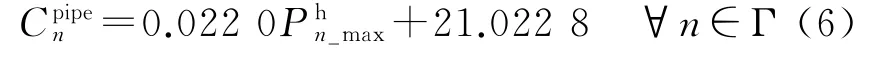
2 多區域分布式能源站供能管線布局規劃

對于區域綜合能源系統規劃建設,一般為了節約城市地下空間,減少能源管線建設過程中反復開挖路面對環境交通帶來的影響,工程管線通常沿交通道路的邊緣進行布局。同時,能源站站址的選擇過程還需要滿足當地地理環境、資源條件、市政規劃限制的情況,結合當地資源稟賦與用地規劃信息對各能源站的位置進行初選。因此,能源站站址以及供能管線的布局應充分考慮區域資源條件與市政道路網絡現狀進行規劃。

基于上述分析,本文將能源站供能路徑與實際交通道路進行結合,將沿道路鋪設供能路徑的最短距離作為能源站供能的最短距離,其規劃示意圖如圖3所示。

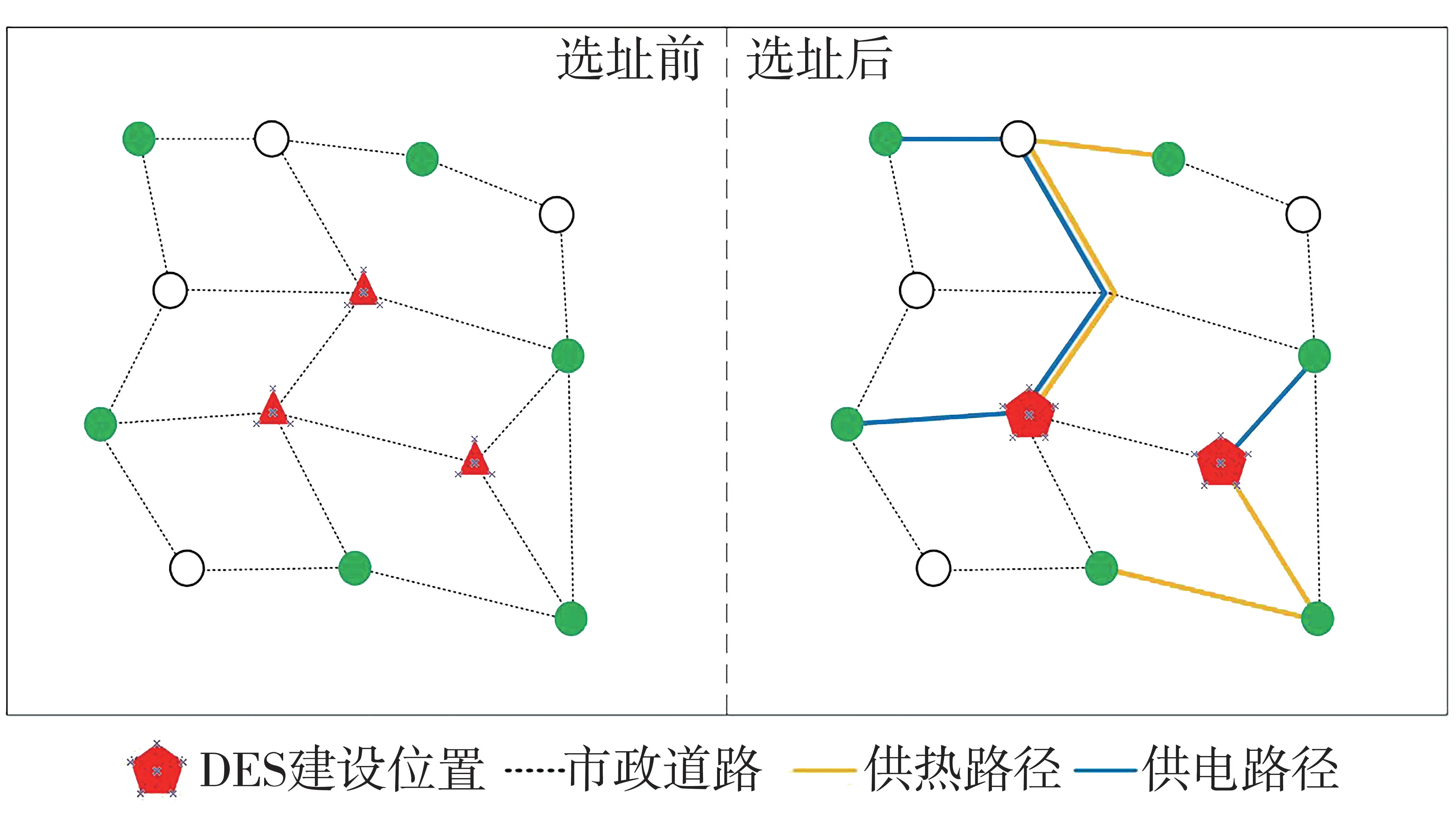
圖3 基于道路網絡的多能源DES選址問題

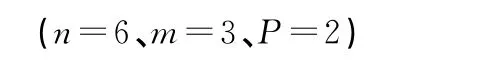
通過Dij kstra最短路徑求解算法計算道路網絡中各負荷節點到各能源站候選位置的最短距離[11]。其中,Dijkstra算法的基本原理在于,在特定網格中,從源節點s按路徑長度遞增次序,通過循環逐條產生最短路徑。

通過這個方法,可以得到沿道路網絡各負荷節點到各能源站候選位置的最短距離dnromad。通過多能負荷需求系數an替代原P-中值模型能源需求量an、通過dnromad替換原P-中值模型中的直線最短距離dnm,就可以得到以DES供能管網投資總成本最低為目標,既能體現綜合能源系統負荷多能需求,又能實現供能管線沿道路布局規劃的DES改進P-中值模型

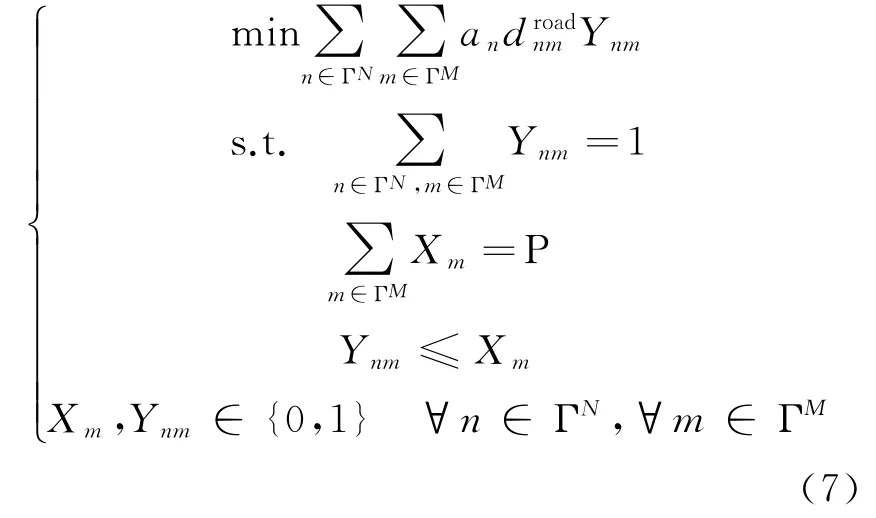
3 模型求解

可以看出,本文所建立的DES選址與供能管線布局規劃模型為混合整數線性模型,相比較非線性模型,線性模型具有求解精度高、時間快的優點。同時,對于不符合要求的方案,還有利于修正規劃參數,快速的得到規劃結果。

利用MATLAB中YAL MIP求解器調用CPLEX算法對本模型進行求解[12],求解流程如圖4所示。

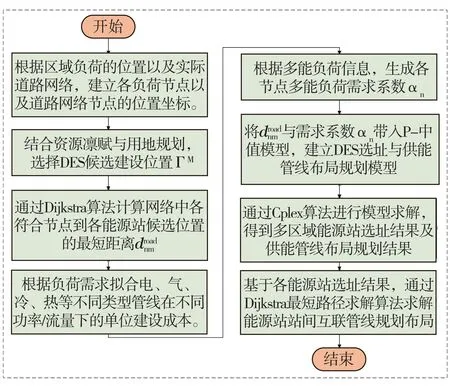
圖4 規劃模型求解流程

4 算例分析

以圖1所示某地區為例進行研究,該區域包含辦公區、居民區2個區域,各區域多能負荷的位置以及道路網絡結構相對位置如圖5所示,共包含16個多能負荷節點具有電、熱能源需求。

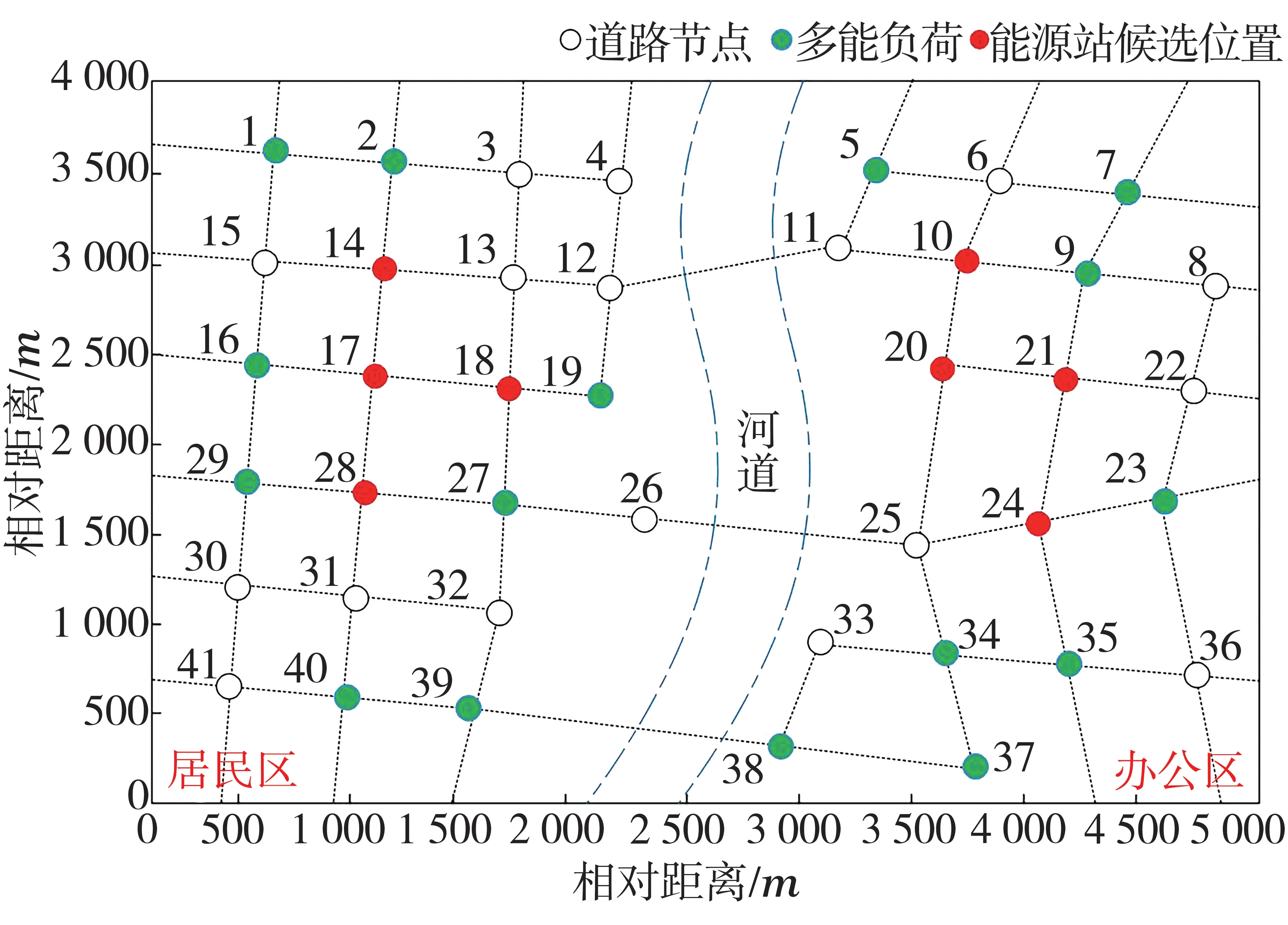
圖5 多能負荷及能源站候選位置示意

各負荷節點夏季、冬季、過渡季負荷曲線如圖6-圖7所示。

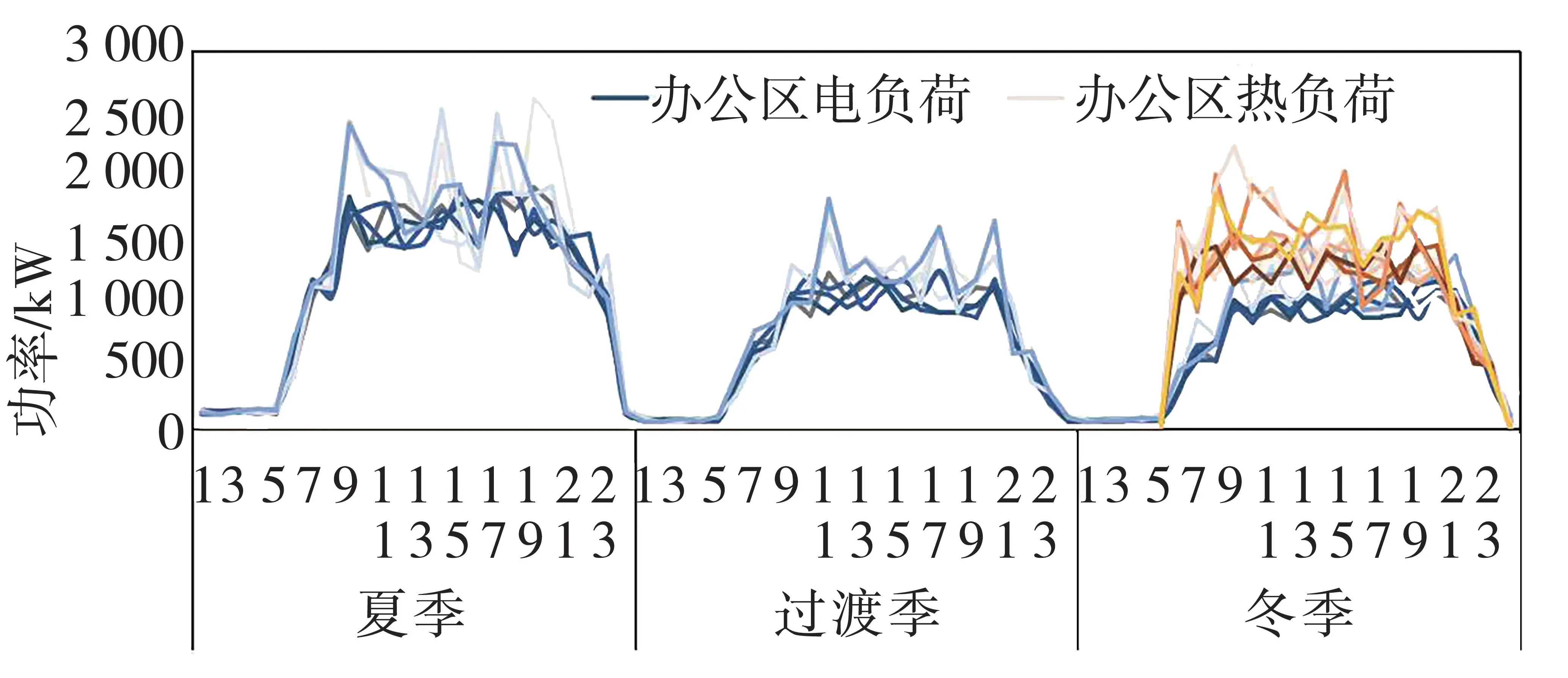
圖7 辦公區各節點電、熱負荷示意

結合當地資源稟賦與建設規劃,擬建設2座能源站以滿足負荷的電、熱供能需求,能源站初選位置如圖6所示。

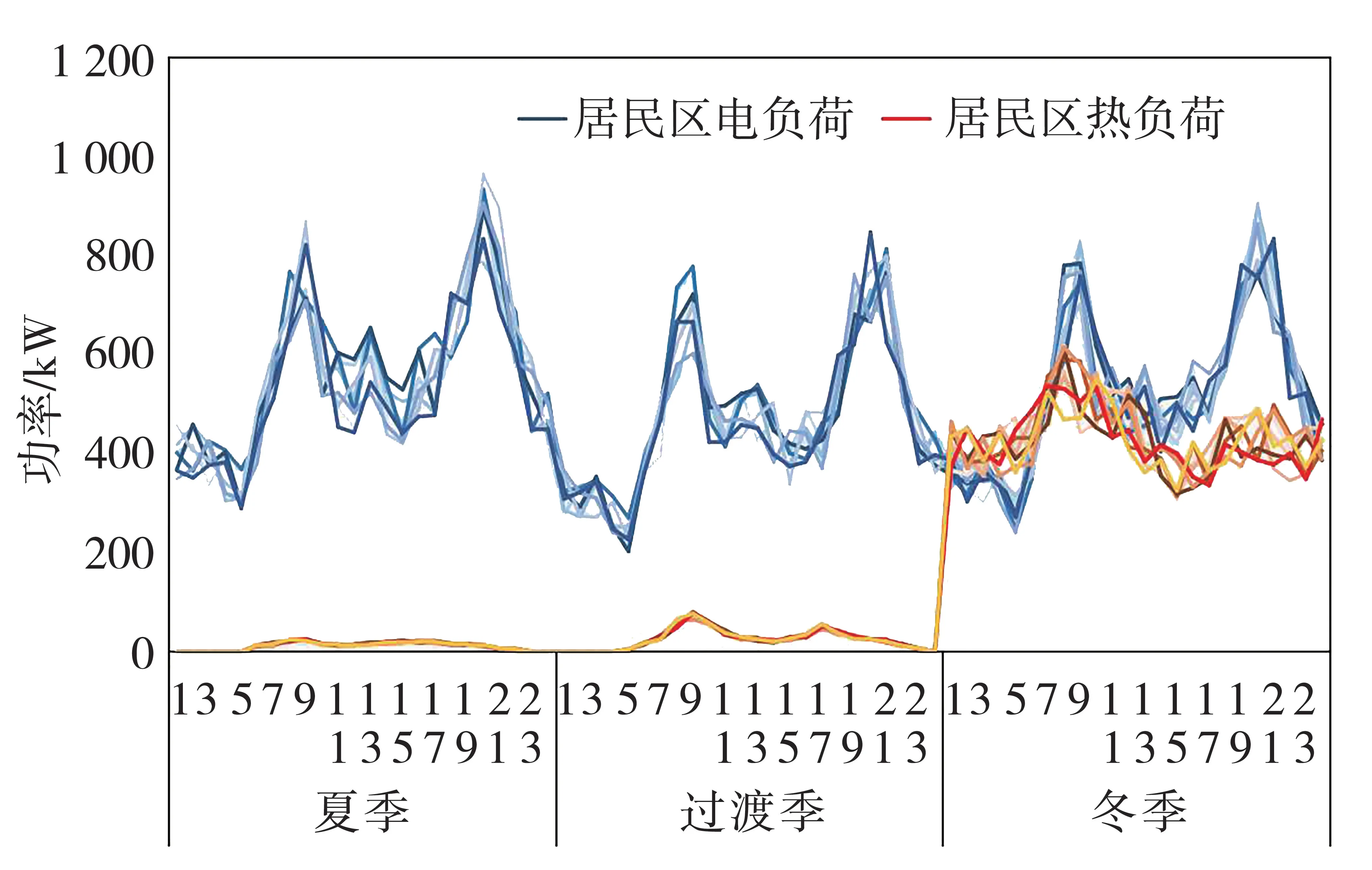
圖6 居民區各節點電、熱負荷示意

通過規劃算法進行求解,可以得到能源站選址規劃結果以及供能管線的布局結果。結果如圖8所示。可以看出,在已知負荷需求及地理信息的情況下,本文所提出的算法可以求解出能源站的建設位置及能源站-負荷間的供能管線布局,以滿足系統對于能源需求的多樣性以及建設經濟性的要求。同時,供能路徑確定后還可以計算出各個能源站供能需求的總量,為后續能源站設備配置、選型規劃建立基礎。

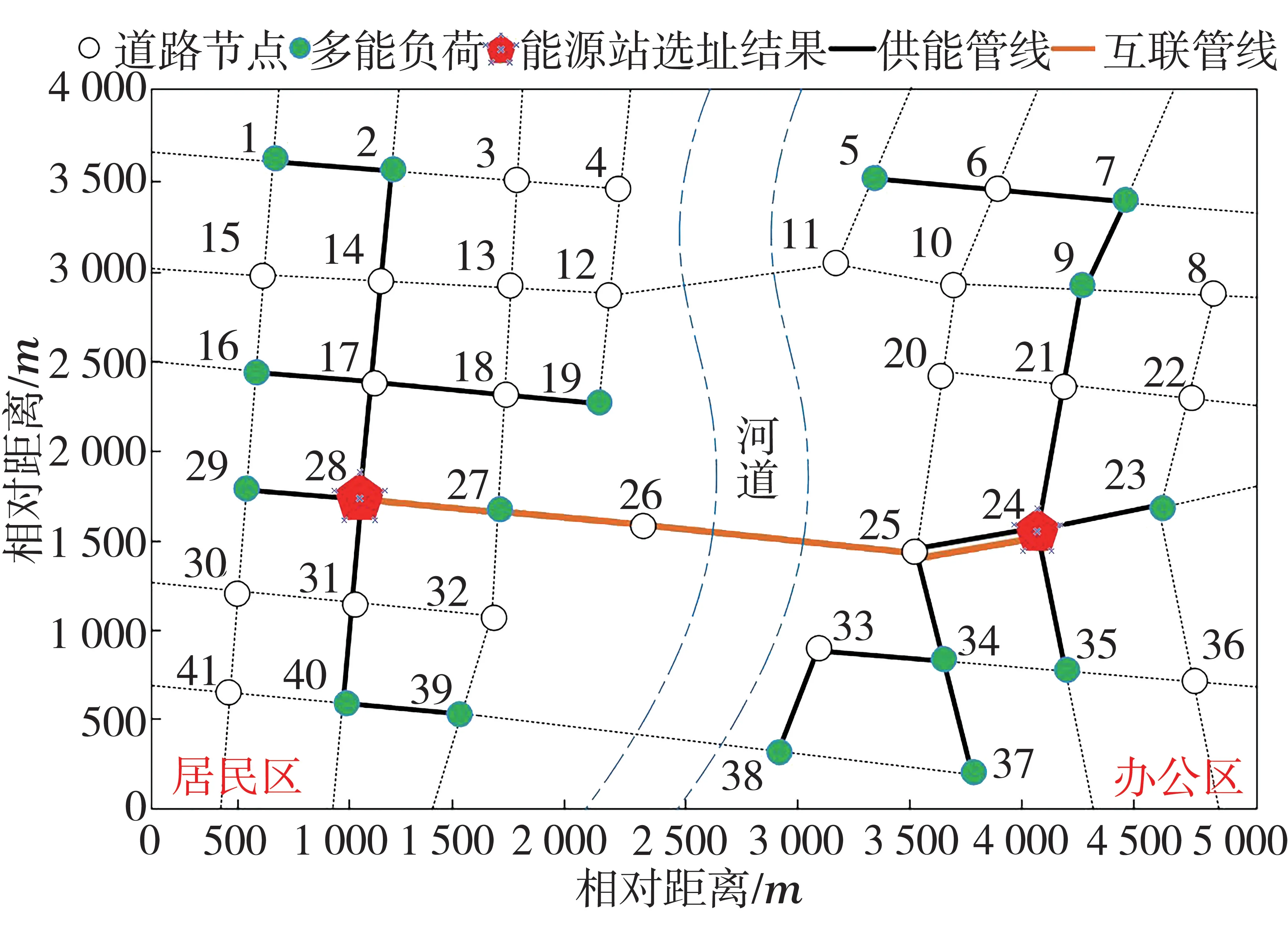
圖8 能源選址及供能管線布局規劃結果

將2座能源站的選址位置坐標帶入Dijkstra最短路徑求解算法進行求解,可以得到能源站站間互聯管線的布局規劃結果,如圖8所示。互聯管線的布局將為后續多能源站互聯系統運行優化,經濟性計算建立基礎。

5 結論

針對多區域分布式能源站選址及供能管線布局規劃問題。本文以傳統P-中值模型為基礎,通過Dij kstra最短路徑求解算法將能源站選址與能源管線布局規劃相結合,引入多能負荷需求系數體現了綜合能源系統中負荷對于不同能源需求的差異(電、氣、冷、熱等)。算例結果表明,本文所提出的規劃方法可以實現能源站選址及能源站-負荷、站間網絡的布局規劃,規劃結果貼合實際,具有良好的經濟效益,可以為后續多區域分布式能源站設備配置、運行優化建立基礎。

在后續研究中,將考慮用戶負荷波動、可再生能源不確定性等因素對規劃的影響。同時,將考慮設備所有權、建設年限以及能源費用變化對規劃結果的影響。