海堤外坡坡度對波浪溢流量的影響*

黃飛揚，潘 毅，周子駿，姜 昊，陳永平

(1.河海大學 水利水電學院，江蘇 南京 210024；2.河海大學 港口、海岸與近海工程學院，江蘇 南京 210024；3.南京水利科學研究院，江蘇 南京 210029)

波浪溢流[1]是指沿海地區極端高水位和熱帶氣旋產生的風暴潮導致海堤堤前水位超過堤頂、海堤受到越浪與溢流聯合作用的現象[2]。在全球氣候變暖的背景下，極端氣候事件發生的強度和頻率都在不斷增加[3]，這使得發生波浪溢流現象的概率也進一步提高。波浪溢流一旦發生，極易引起大規模的潰堤災難[4]。2005 年“卡特里娜”颶風風暴潮期間，美國墨西哥灣沿岸由于波浪溢流產生的海堤內坡侵蝕破壞就多達43 處[5]，大量的村莊和農田被海水沖毀。自此波浪溢流現象受到了海岸工程界學者的高度重視，波浪溢流也成為了海堤設計和安全評估中必須考慮的因素。

波浪溢流量是指波浪溢流引起的平均單寬越堤流量，是波浪溢流與海堤防護相關的最重要的水力學參數。自2005 年的“卡特里娜” 颶風風暴潮以來，國內外學者對此做了大量研究。2007 年出版的《歐洲越浪手冊》[6]最早提出了波浪溢流量的計算方案，此方案作為波浪溢流災害的應急處理方式直接將波浪溢流量視為穩定溢流量和越浪量的線性疊加；2008 年Reeve 等[7]基于雷諾時均的N-S 方程建立了數值水槽模型來研究不可滲透海堤的波浪溢流量，通過模擬結果擬定出無量綱波浪溢流量表達式；2009 年Hughes 等[8]在幾何比尺為25∶1 的梯形截面海堤模型上開展了一系列波浪溢流水槽試驗，給出了運用相對出水高度Rc∕Hm0計算波浪溢流量的方法；2012 年Li 等[9]分析大型水槽試驗結果，得到了后坡材料為不透水碾壓混凝土的波浪溢流量擬合曲線。

雖然Hughes 和Nadal 建立了利用相對出水高度計算波浪溢流量的方法，但是將影響波浪溢流量的原因只歸結于溢流與越浪的占比問題；而后Li 等采用了大型水槽模型也得到了不透水海堤平均波浪溢流量曲線，并且在此基礎上分析了不同相對出水高度條件下波浪和溢流對波浪溢流量的主導作用。但是上述物理試驗都是在外坡坡度為1∶4.25的海堤模型中開展的，忽略了外坡坡度在計算波浪溢流量中的作用。然而van der Meer[10]在越浪的有關研究中指出了海堤外坡坡度對越浪量存在較大影響；波浪溢流作為一種極端的越浪，與越浪過程有很多共同點，海堤外坡坡度對波浪溢流也會存在一定影響，尤其是當水位高于堤頂數值不大時。因此，筆者在現有研究的基礎上，采用水槽試驗的方式，探討了海堤外坡坡度對波浪溢流量的影響，提出了考慮海堤外坡坡度的波浪溢流量計算公式。此次研究成果提高了對波浪溢流量的估算精度，能夠為波浪溢流期間海堤防御的相關研究和工程措施提供參考依據。

1 波浪溢流模型試驗

波浪溢流模型試驗在南京水利科學研究院河流海岸所的波浪水槽中進行，在距離造波機53 m處按照1∶10 的試驗比尺布置海堤模型，各水力學參數依據弗勞德相似準則進行換算。該物理試驗的海堤模型采用了PVC 板制作，中間設置鋼架并填充沙石進行固定，接縫處做防水處理以保證模型整體為光滑不透水結構。模型高度為0.325 m、堤頂寬為0.260 m、后坡坡度為1∶3。試驗的波浪溢流模擬及流量測量系統包括水槽進出水泵、雙向泵、接水箱(包括配套的出水泵)、造波機、水位儀、波高儀、流速儀等。模型布置見圖1。

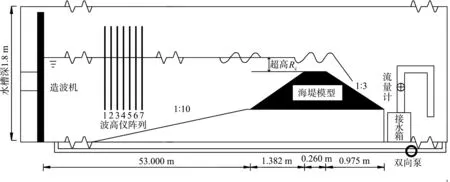
圖1 水槽和海堤模型

試驗開始時，首先開啟水槽進水泵將水槽充水至堤頂，然后開啟雙向泵產生順波向水流，此時堤前水位升高、堤后水位迅速降低，從而產生溢流。當溢流穩定后，調節雙向泵和水槽進、出水泵控制流量，使得堤前水位達到試驗工況所設定的超高，并在堤后形成自由出流。生成穩定的溢流后，開啟造波機產生規定波浪要素的波浪(試驗采用不規則波，不規則波譜為JONSWAP 譜)。由于本試驗的波浪周期較多，為了盡量減少波高儀的移動、提高試驗效率，在海堤模型外坡側安裝7 根電容式波高儀(圖1)，其中數據采集和處理采用DJ800 多點波高儀測量系統，該系統可以實現多個波高傳感器的同步測量，誤差絕對值小于0.1 mm。整個波高儀測量系統距海堤模型最遠距離為6.0 m、最近距離為4.8 m，對不同周期的波浪，至少保證有3 根波高儀滿足入、反射分離的間距要求。對于波浪溢流量的測量，由于堤頂水流流速較大且水體較薄，使用流速儀和波高儀測量水流流速和厚度的誤差較大，所以本次試驗先使用接水箱接取越堤水流，然后再通過流量計抽取箱中水體來間接計算平均波浪溢流量。試驗組次見表1，其中海堤外坡坡度為m，有效波高Hm0為不規則波按波高大小次序排列后取前面1∕3 個波的平均波高，譜峰周期Tp定義為JONSWAP 譜中最大譜值所對應的周期，模擬時長T為不規則波到達海堤并且流量變化較為穩定后直至測量結束的試驗時長。

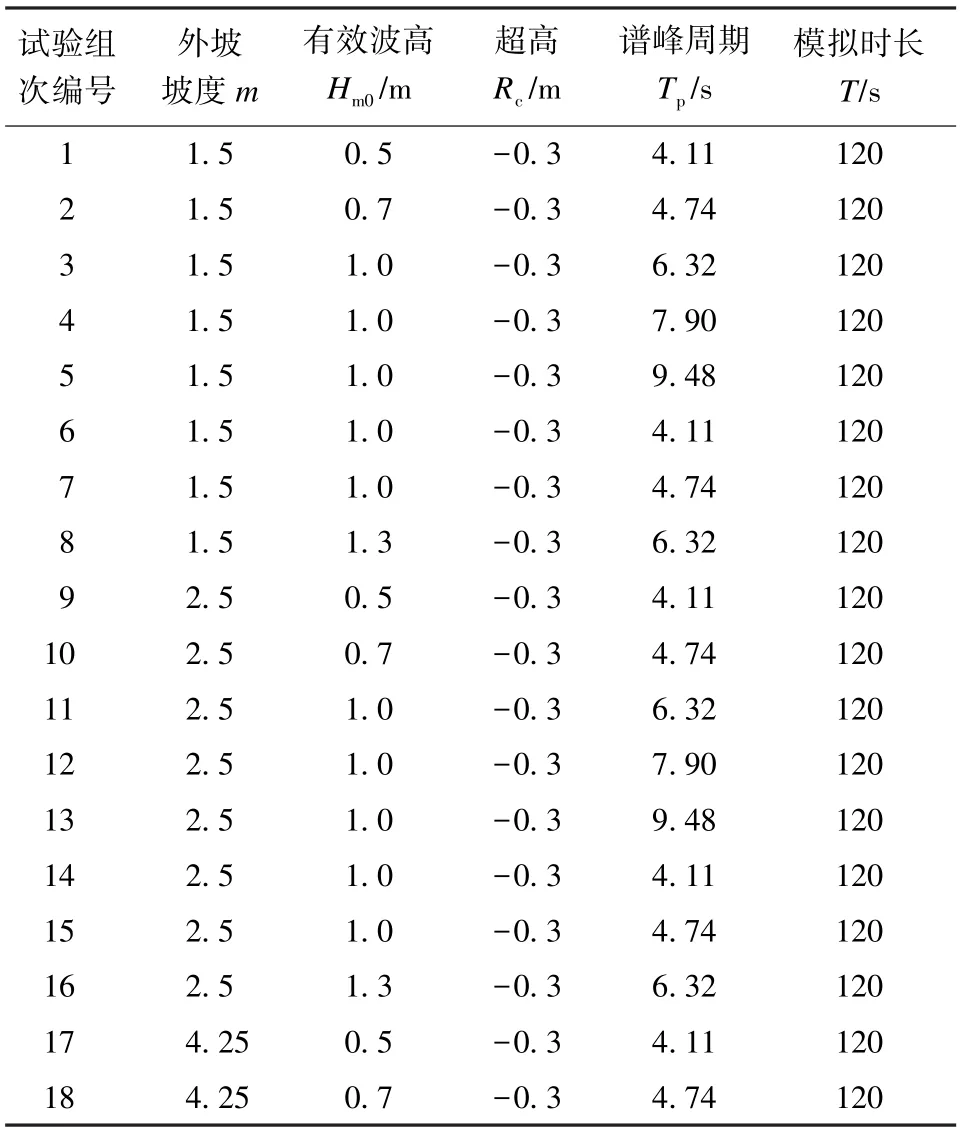
表1 試驗組次

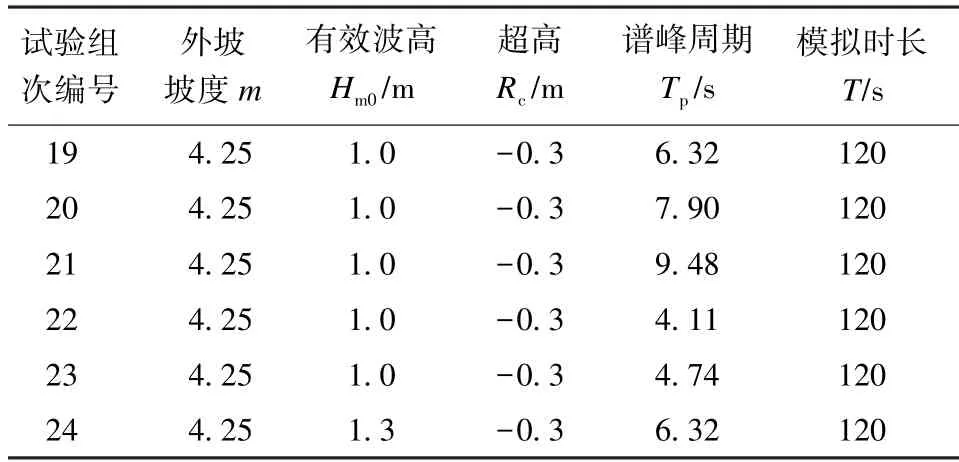
續表1

2 海堤外坡坡度對波浪溢流影響分析

波浪溢流越堤流量是波浪溢流與海堤相互作用研究中最基本的參數。疊加于海堤穩定溢流上的波浪作用將直接影響越堤水流的形態和大小，在波浪溢流相關研究中主要通過Iribarren 數ξp(即海堤坡度與波浪波陡的比值)判斷波浪破碎形式，特別是在堤頂水深較小的情況下，海堤剖面形狀結構將會直接改變波浪溢流的越頂方式。本文基于上述物理試驗模型，在相同波陡的情況下，通過改變海堤外坡坡度和波浪溢流超高，來觀察試驗中波浪破碎形式，試驗現象見圖2。

圖2 不同外坡坡度下波浪溢流作用于海堤的過程

由圖2 可見，當超高絕對值較小時(｜Rc｜＝0.03 m)，穩定溢流疊加波浪后，隨著海堤外坡變陡，波浪在堤前破碎程度逐漸擴大，波浪反射程度減弱，并在堤頂前沿發生卷破破碎，產生了大量紊動流體，同時消耗了大量的波能，損耗能量的增加值遠大于反射能量的減小值，不規則波列中只有個別大波可以不發生破碎越過堤頂沖向后堤。當超高絕對值較大時(｜Rc｜＝0.06 m)，不規則波列中的大部分波浪都能直接越過堤頂，水流狀態基本不發生變化，此時海堤外坡坡度對波浪溢流水流特性作用也逐漸弱化。

為了進一步研究影響波浪溢流量的相關因素，對Hughes 和Nadal(2009)與Li 等(2012)的物理模型試驗數據進行分析，結果見圖3a)，其中橫坐標為超高和有效波高的比值，定義為相對出水高度，縱坐標為波浪溢流量與波浪相關參數進行組合的無量綱波浪溢流量。可以發現在相同海堤外坡坡度的情況下，無量綱波浪溢流量與相對出水高度在Rc∕Hm0≤-0.3 的范圍內具有較好的相關性；而在-0.3＜Rc∕Hm0＜0 時相關性較差，二者試驗數據存在一定的偏差。

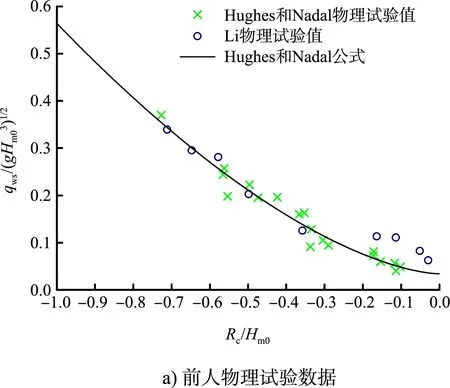
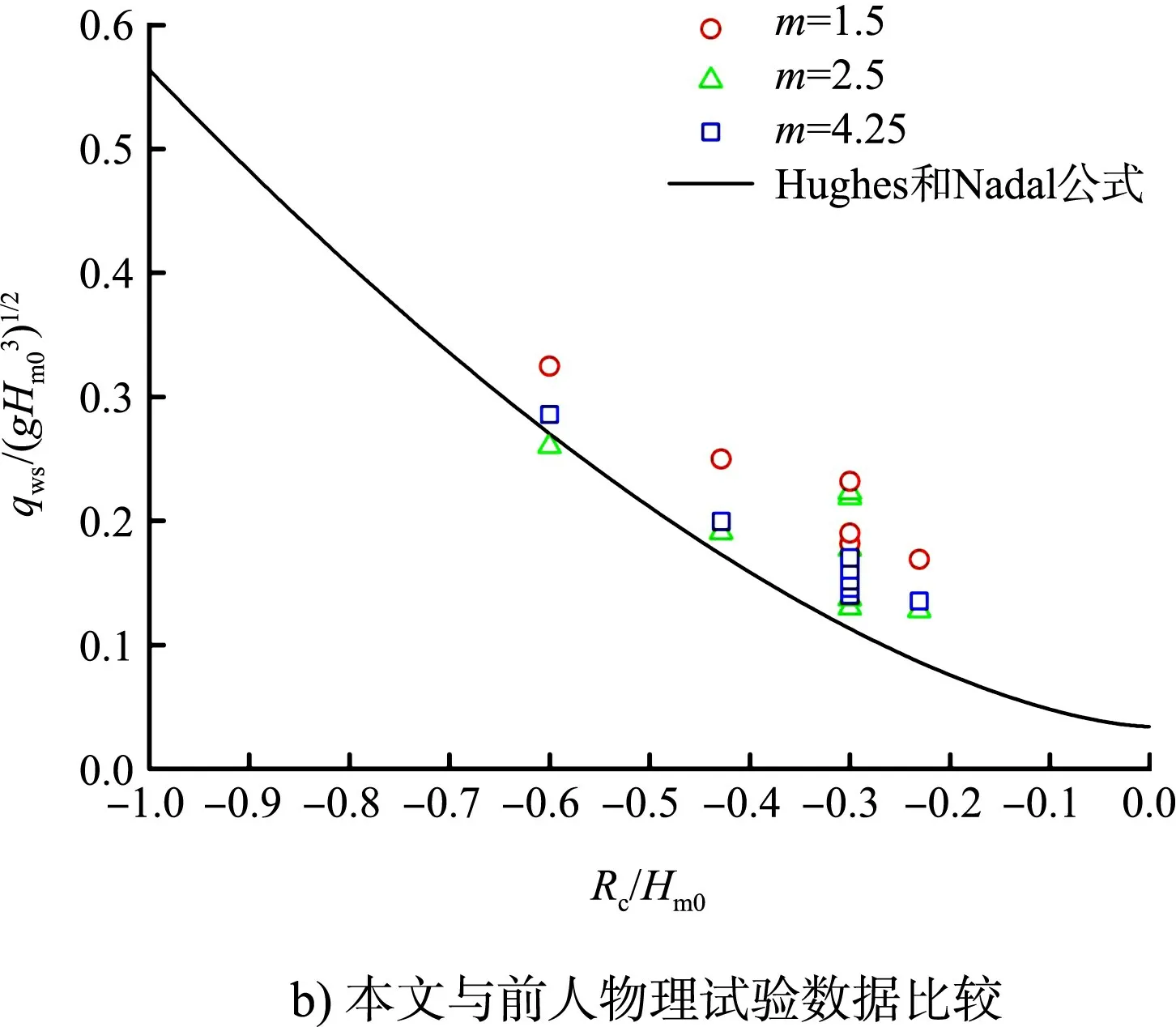
圖3 本文波浪溢流物理試驗數據與前人物理試驗數據比較

通過觀察圖2 的試驗現象并分析圖3a)的試驗數據可知，不同的相對出水高度和海堤外坡坡度都會使波浪溢流的過堤形式發生改變，這種變化在堤頂相對出水高度較大時尤為強烈。利用平均波浪溢流量測量系統，測量不同相對出水高度的波浪溢流，結果見圖3b)。其物理試驗數據分布與Hughes 和Nadal 公式在趨勢上較為吻合。Hughes 和Nadal 公式的表達式為:

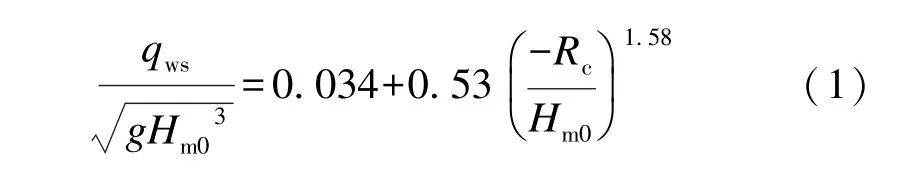
式中:qws為波浪溢流量；Hm0為有效波高；Rc為水位超高；g為重力加速度。

在相同外坡坡度條件下，平均波浪溢流量隨著相對出水高度的增大而減小。當Rc∕Hm0≤-0.3時，m＝2.5 時的試驗數據與Hughes 和Nadal 公式計算結果十分接近；而 當-0.3 ＜Rc∕Hm0＜0 時，m＝2.5 時的試驗數據相較于Hughes 和Nadal 公式計算結果偏大。這主要是由于Hughes 和Nadal 公式中并沒有考慮外坡坡度對波浪破碎形式的影響，使得在計算波浪溢流量時存在偏差。為進一步研究海堤結構對波浪溢流量的作用，分析在不同海堤外坡坡度的情況下波浪溢流量的變化情況，建立了如圖4 所示的不同波高情況下無量綱化平均波浪溢流量qws∕(gHm03)1∕2隨外坡坡度m的變化關系。

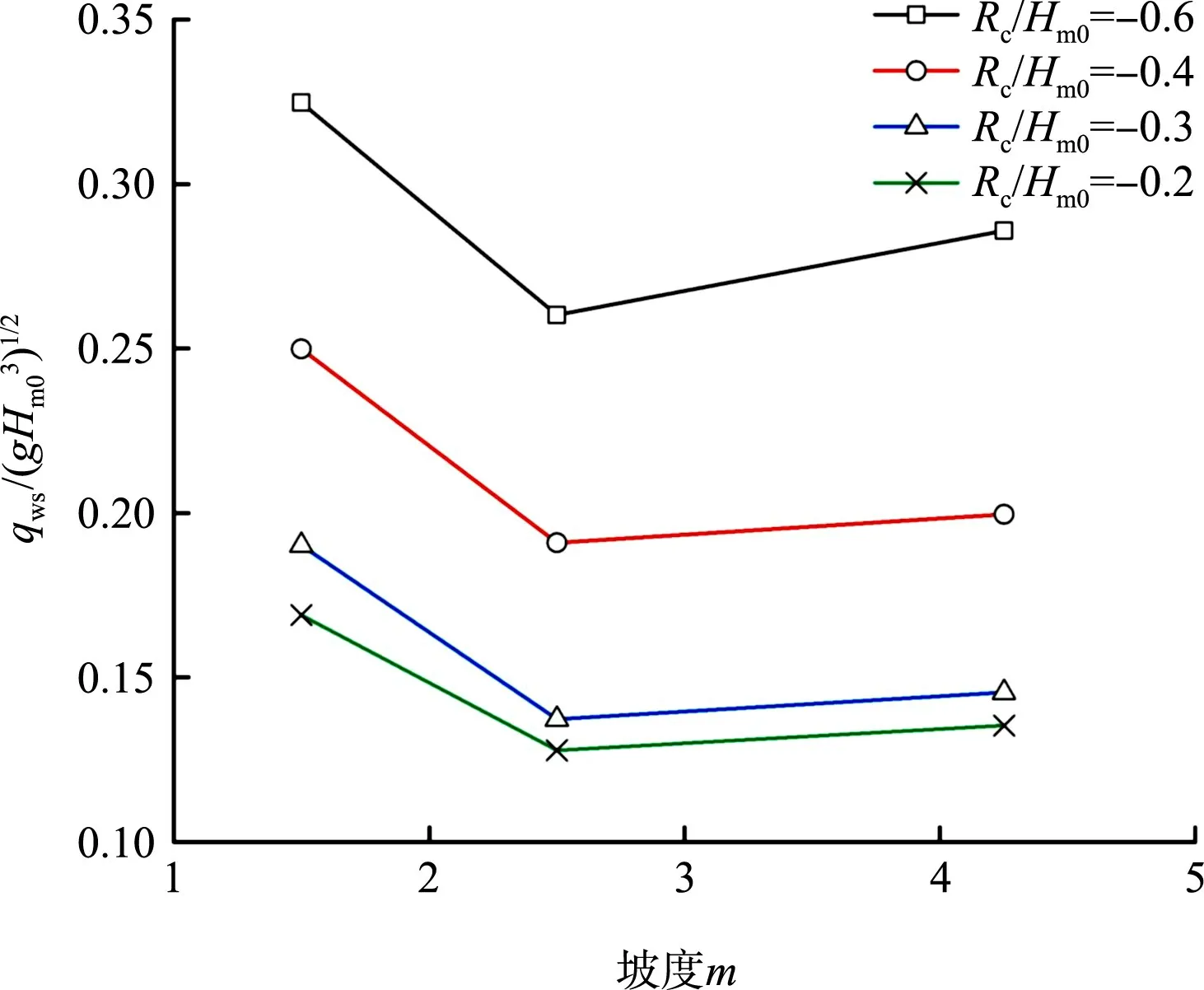
圖4 不同波高情況下平均波浪溢流量qws∕(gHm03)1∕2隨海堤外坡坡度m 的變化

3 考慮外坡坡度的平均波浪溢流量計算公式

由于波浪溢流過程十分復雜，試圖從理論上對平均波浪溢流量推導數學公式常常難以得到滿意的結果，因此，對于此類問題常采用因次分析方法進行分析。影響波浪溢流量的因素眾多，其中相對出水高度是影響波浪溢流量的最主要原因，而當相對出水高度較大時，外坡坡度對波浪溢流量的作用同樣不可忽略。

本文在Hughes 和Nadal 公式基礎上增加坡度影響參數γm，以反映外坡坡度的影響，使得修正后的計算公式能夠考慮到外坡坡度對波浪溢流量的作用。確定平均波浪溢流量計算公式的基本結構形式為:

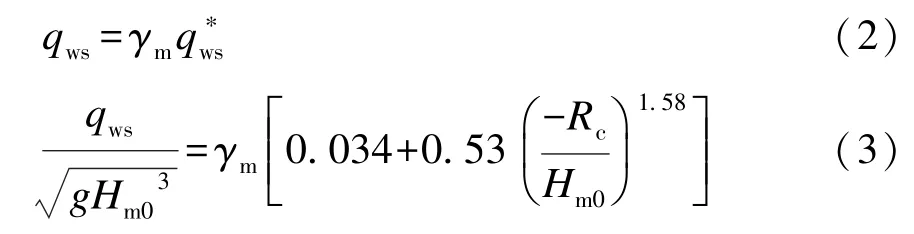
式中:γm為坡度影響參數；qws為考慮外坡坡度影響的平均波浪溢流量測量值；為Hughes 和Nadal 公式中波浪溢流量的計算值；Rc為超高；Hm0為有效波高，g為重力加速度。圖5 給出了不同坡度m分級情況下γm隨相對出水高度Rc∕Hm0的變化關系，并選取相同外坡坡度條件下的試驗數據進行擬合得到相關曲線。在對數據進行擬合時可以發現不同周期下的波浪溢流量也存在差異。

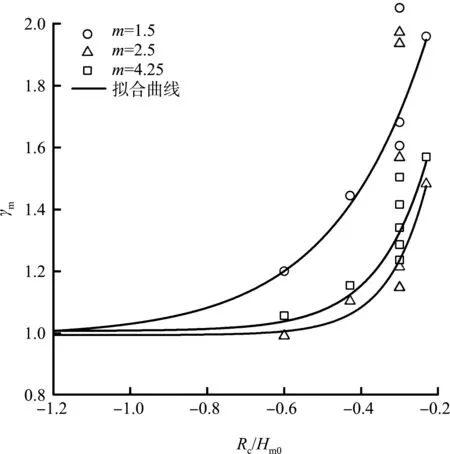
圖5 坡度影響參數γm隨相對出水高度(Rc∕Hm0)的變化

由圖5 可知，當相對出水高度-0.6＜Rc∕Hm0＜0時，不同坡度下的有明顯的差別，隨著相對出水高度Rc∕Hm0的增大，這種差別會更加明顯，此時坡度影響參數γm與Rc∕Hm0成指數關系；當相對出水高度Rc∕Hm0≤-0.6 時，波浪溢流主要由溢流占據主導地位，而溢流量只與堤頂水頭有關，此時外坡坡度對溢流量幾乎沒有影響，所以平均波浪溢流量qws與溢流量qs比值隨著相對出水高度Rc∕Hm0的減小逐漸接近于1。因此，針對不同坡度影響參數γm，可以使用公式(4)對圖5 中的試驗數據進行處理:

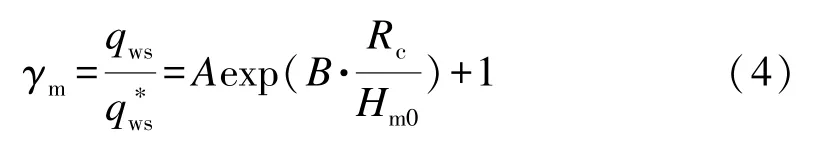
式中:A、B為經驗參數，可根據不同外坡坡度條件下的平均波浪溢流量進行確定；γm為坡度影響參數；qws為考慮外坡坡度影響的平均波浪溢流量測量值；為Hughes 和Nadal(2009)公式中波浪溢流量的計算值；Rc為超高；Hm0為有效波高。

將試驗測量的數據代入式(4)，分別求解出經驗參數A、B的值，計算結果見表2。

表2 不同坡度m 下經驗參數A、 B 的值

為了得到不同外坡坡度m下的A、B值，可以通過表2 數據對經驗參數A、B進行多項式數據擬合，得到的擬合曲線見圖6。

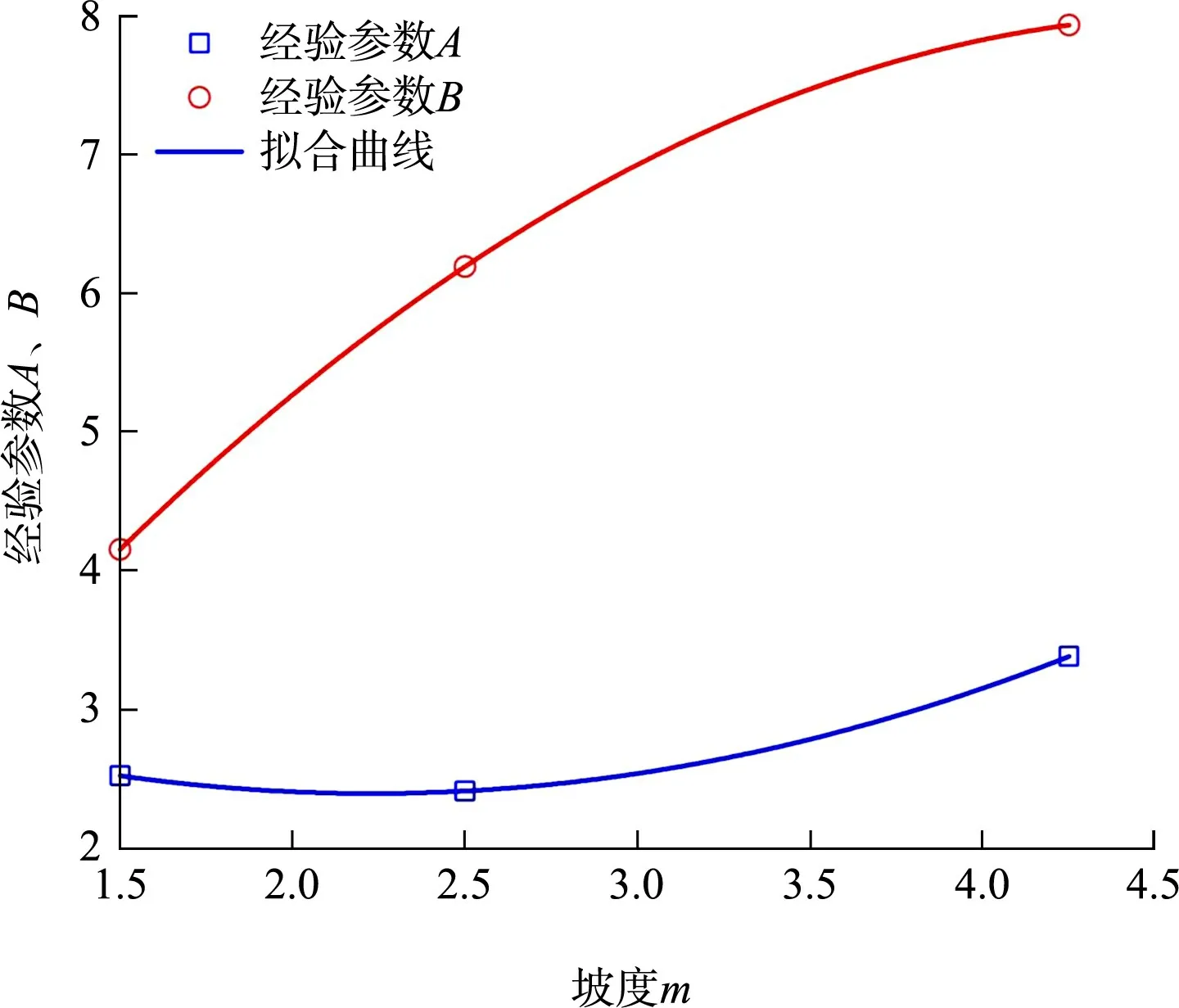
圖6 經驗參數A、 B 隨外坡坡度m 的變化關系

圖6 中經驗參數A、B的擬合公式為:

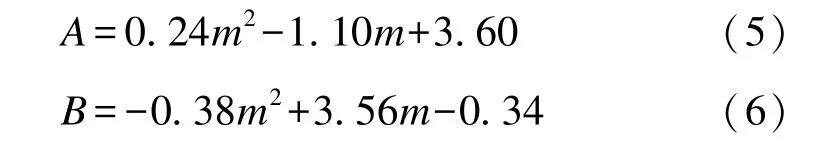
采用本文物理試驗、Hughes 和Nadal 的物理試驗、Li 的物理試驗結果對公式(3)～(6)進行驗證，驗證結果見圖7。平均波浪溢流量計算值與各物理試驗測量值相關性較好，相較于Hughes 和Nadal 公式加入坡度影響因素的無量綱波浪溢流量公式計算精度更高；Li 的物理試驗數據在無量綱波浪溢流量較大條件下與公式計算值相關性較好，而在無量綱波浪溢流量較小的條件下二者相關性較差。由上述分析可知，公式計算值與各物理試驗值之間相對偏差都不超過20%。利用本文加入海堤外坡坡度因素影響下的波浪溢流量試驗數據對公式(3)的計算誤差進行統計，得出公式(3)的決定系數R2為0.993、均方根誤差RMSE 為0.344。結果表明公式(3)的計算結果與試驗數據吻合，因此公式(3)可以運用到實際波浪溢流量的計算當中。值得注意的是，當無量綱波浪溢流量qws∕(gHm03)1∕2數值小于0.1 時，公式(3)的計算值有所高估，其原因為該范圍的數據點超出了試驗的研究范圍(如圖7 中三角形符號所標識的數據范圍)，因此在超出本試驗研究范圍的情況下，應謹慎使用本文提出的公式。

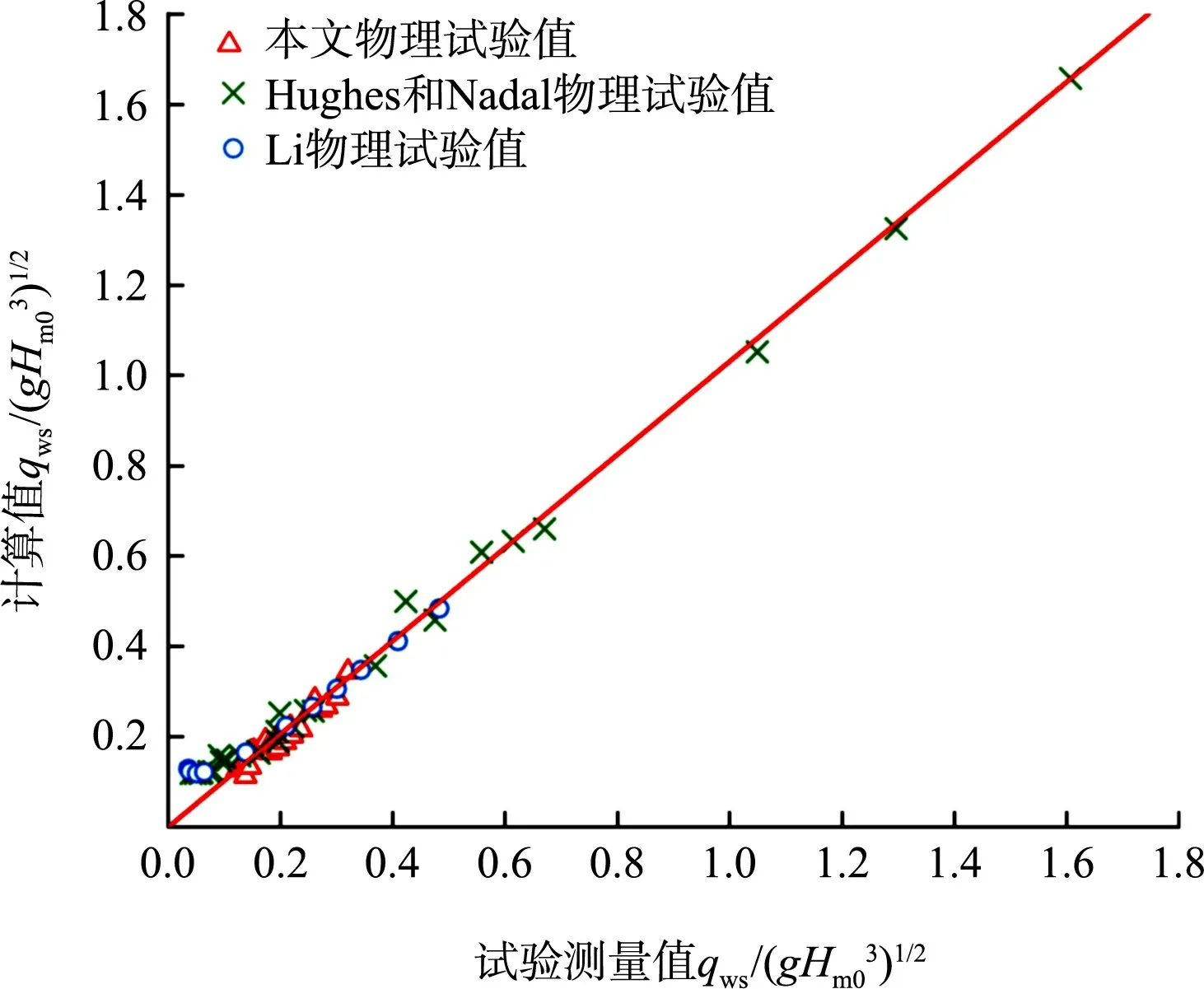
圖7 平均波浪溢流量計算值與試驗值的比較

4 結論

1)相對出水高度Rc∕Hm0的大小影響海堤外坡坡度對波浪溢流量的影響程度。在-0.6＜Rc∕Hm0＜0的范圍內，海堤外坡坡度對波浪溢流量產生明顯影響；而在Rc∕Hm0≤-0.6 的范圍內，海堤外坡坡度對波浪溢流量影響可以忽略。

2)在-0.6＜Rc∕Hm0＜0 的范圍內，海堤外坡坡度影響到越堤水流形態，進而對波浪溢流量產生影響。海堤外坡坡度從1∶1.5 到1∶4.25 變化的過程中，同等波浪條件下的波浪溢流量呈現先減小后略有增加的趨勢。根據試驗現象觀測，海堤外坡坡度從1∶1.5 變化到1∶2.5 時，波浪溢流量的減小是由于波浪破碎程度的增加消耗了水體爬高的動能；而隨著坡度繼續變緩，波浪溢流量略有增加則是由坡度變緩引起的波浪爬高增大引起。

3)Hughes 和Nadal 公式未考慮外坡坡度對波浪溢流的作用，但在1∶4.25 的海堤外坡坡度下表現較好，因此本文在Hughes 和Nadal 公式基礎上增加坡度影響因子γm以反映外坡坡度的影響，擬合得到了包含海堤外坡坡度m的平均波浪溢流量公式(3)，該公式可以計算不同外坡坡度下的平均波浪溢流量，拓展了波浪溢流量的計算范圍。應當注意的是，在超出本試驗研究范圍的情況下，應謹慎使用本文提出的公式。