基于改進多目標粒子群算法的平原坡水區水資源優化調度

王文君，方國華，李 媛，聞 昕，郭玉雪

(1.河海大學水利水電學院，江蘇 南京 210098； 2.南京水利科學研究院水工水力學研究所，江蘇 南京 210029)

平原坡水區大都是糧棉油的主要生產基地[1]，但平原坡水區河道坡度十分平緩[2]，河流密布，流動性復雜，再加上自然條件和其他因素的影響，致使流域內攔蓄能力不足，沒有大型蓄水工程，水源無保證，區域水系難以形成聯合調配體系、區域內水資源供需關系緊張、缺水問題突出，嚴重影響了沿線經濟發展。另一方面，平原坡水區有大量的泵、閘、渠等水利工程，能夠擔負起水資源調配的綜合性任務[3]。如何充分發揮水工建筑物效能、河道蓄水能力，改善灌排工程體系，統籌利用天然徑流和外調水進行優化調度，結合受水區需水情況對水量進行優化分配，實現區域多水源的互濟互調，在降低受水區缺水率的同時，充分發揮生態效益和經濟效益是亟待解決的問題[4]。

水資源優化調度往往涉及多個目標[5]，常用的線性規劃、動態規劃、大系統分解協調等解法在處理多目標復雜系統時的求解效率難以滿足實際需求。近年來發展起來的模擬生物演變過程的智能優化算法逐漸成為求解水資源優化調度模型的主要手段，主要有遺傳算法(GA)[6-8]、粒子群(PSO)算法[9]、蟻群算法(AG)[10]等。NSGA-Ⅱ算法是遺傳算法中最具代表性的方法[11]。該算法基于1993年Srinivas和Deb提出的NSGA算法，改進了解集的構造，提高了求解效率，并保證了解集的有效性和優越性[12-13]。粒子群算法則具有結構簡單、易于實現、搜索速度快等優點[14]，很多學者將其運用于水資源調度并取得了一定的效果。閆堃等[15]利用多目標粒子群(multi-objective particle swarm optimization， MOPSO)算法求解濱海地區平原河網、平原水庫群和遠距離調水工程體系的水資源多目標優化調度模型。王萬良等[16]采用多目標混合粒子群算法求解梯級小水電群動態多目標優化調度模型。翁士創等[14]將粒子群算法應用于旱情緊急情況下的韓江流域水資源調度模型，取得了較好的綜合效益。

針對PSO算法存在容易陷入局部極值點、早熟等缺點，本文從慣性因子及學習因子選擇、外部檔案維護以及全局最優選取策略3個方面進行改進，對比傳統的NSGA-Ⅱ算法，測試改進MOPSO算法在部分ZDT函數上的表現，驗證算法的可行性及優越性，最后以宿遷市黃河故道及以南地區水資源優化調度為例，采用改進MOPSO算法求解平原坡水區水資源優化調度模型。

1 平原坡水區水資源優化調度數學模型

為實現期望效益，提高泵閘運行經濟效益，模型選取受水區缺水量和泵站提水量兩個優化目標，將生態目標轉化為約束條件進行處理[17]。根據平原坡水區系統構成和特點考慮河道水量平衡約束、泵站工作能力約束、閘站下泄流量約束、河道調蓄能力約束、河道水位要求約束、生態約束和非負約束，構建平原坡水區水資源優化調度模型。

1.1 目標函數

1.1.1經濟目標

在充分利用現有水資源的前提下，區域用水不足的部分由區域內泵站提水補充，總提水量越小，則越能有效控制提水成本，因此經濟目標取總提水量最小為目標，目標函數為

(1)

式中：t為時段序號；T為時段數；a為泵站編號；m為泵站數量；Pa,t為t時段泵站a的提水量。

1.1.2社會目標

社會目標可以通過總缺水量大小來衡量，因為區域用戶缺水量關系社會發展和人民的生活水平，進而影響社會效益。其目標函數為

(2)

式中：b為分區編號；n為分區數量；Db,t為t時段b分區的缺水量。

1.2 約束條件

a.河道水量平衡約束。針對有調蓄能力的河道，應滿足的水量平衡方程為

Vi,t+1=Vi,t+WPi,t+Wi,t+WXi-1,t-WRi,t-WXi,t

(3)

式中：Vi,t為t時段河道i的蓄水量；WPi,t為t時段抽過境水入河道i的泵站提水量；Wi,t為t時段流入河道i的天然徑流和地下水資源量；WRi,t為t時段河道i的供水量；WXi,t為t時段河道i的下泄水量。

b.泵站工作能力約束：

0≤Pa,t≤Pa,t,max

(4)

式中Pa,t,max為t時段泵站a的最大工作能力。

c.閘站下泄流量約束：

0≤Xl,t≤Xl,t,max

(5)

式中：l為閘站編號；Xl,t、Xl,t,max分別為t時段閘站l的下泄流量和最大下泄流量。

d.河道調蓄能力約束：

Vi,t,min≤Vi,t≤Vi,t,max

(6)

式中Vi,t,min、Vi,t,max分別為t時段河道i的最小和最大蓄水能力。

e.河道水位要求約束：

Zi,t,min≤Zi,t≤Zi,t,max

(7)

式中Zi,t、Zi,t,min、Zi,t,max分別為t時段河道i的水位、最低水位和最高水位。

f.生態約束：

Qi,t≥QEi,t,min

(8)

式中Qi,t、QEi,t,min分別為t時段河道i的流量和所要求的最小生態環境流量。

g.非負約束。所有參數滿足非負約束條件。

2 改進MOPSO算法

2.1 PSO算法

PSO算法是基于鳥群覓食行為發展起來的一種以群體協作及信息共享為基礎的智能搜索算法[18]。在該算法中每個粒子的速度和位置按照如下方程來更新：

(9)

(10)

式中：k為迭代步數；vs,d為粒子s在d維空間上的速度，vs,d∈[vmin,vmax]；w為慣性因子；c1、c2為學習因子，通常取c1=c2=2；r1、r2為[0,1]范圍內的均勻隨機數；ps,d為粒子s在d維空間上的個體極值點；pg,d為d維空間上的全局極值點；xs,d為粒子s在d維空間上的位置。

2.2 慣性因子和學習因子的選取

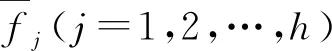
日灼病是因為陽光太強、溫度過高導致植株葉肉細胞灼傷失去活性，從而減弱苗木整體生長勢的一種生理病害[3-4]。由表4可知，圃地內設置的對照組大棚沒有覆蓋，通過一個夏秋季，苗木日灼現象嚴重。可見，低海拔地區香榧育苗和栽培時沒有遮蔭措施是不行的，遮蔭措施可以有效把直射光轉成散射光或漫射光線，極大減輕了苗木日灼病發生。

(11)

式中：wmax、wmin、wmid分別為慣性因子最大值、最小值和中間值，本文分別為3.0、-1.0和1.0；fj,s為粒子s的適應度值；h為目標函數的總個數。該策略保證種群中的每個粒子都能朝正確的方向飛行，更快地趨近Pareto前沿。

本文采用的粒子群算法依據迭代步數調整學習因子，具體策略為

(12)

式中：k為當前迭代步數；kmax為最大迭代次數。c1隨迭代步數的增加遞減，而c2則與之相反。該策略使粒子在飛行前期更注重本身的歷史軌跡，而飛行后期則更注重種群的位置信息。本文cmax和cmin的取值分別為2.0和0.5。

2.3 全局最優選取策略

由于缺乏標準方法判斷多目標優化問題中非劣解集的優劣，本文采用基于距離的方法選取全局最優pg,d，即全局極值點。假設A和B是外部檔案中的2個非劣解，則A和B在目標空間的距離定義為

(13)

對于檔案中的非劣解A，采用改進的MOPSO算法尋找與A最近的2個解C和D，并得出A的特征距離：

(14)

比較所有非劣解的特征距離并尋找特征距離最大的解作為全局最優。如果幾個解的特征距離相同則從中隨機選取全局最優。該策略能夠避免粒子群陷入局部最優，從而更加接近Pareto前沿。

2.4 外部檔案的初始化和維護策略

改進MOPSO算法依據解的支配關系和距離關系來實現外部檔案的維護。解之間的支配關系定義為：對于A和B兩個解，若A的全部目標函數均不大于B的目標函數，且至少有一個目標函數小于B，那么A解支配B解；反之則B解支配A解。若以上兩個條件均不滿足，則兩者互不支配。

程序開始時將粒子逐個放入外部檔案，依次比較粒子與檔案中已有的解。若粒子支配檔案中的某個解，則刪除檔案中的該解。假如檔案中不存在支配該粒子的解，則把這個粒子放入檔案。

同樣，每次更新粒子的速度和位置取得新解之后，依照上述規則將其與檔案中已存在的非劣解進行比較，在不被檔案中任一解支配時在檔案中放入該解。如果檔案中成員的數量超過程序設定值，則比較檔案中所有解之間的擁擠程度，并隨機刪去距離最近的兩個解中的一個，而后重新計算解成員之間的距離。

2.5 算法基本流程

改進MOPSO算法的基本流程如圖1所示。

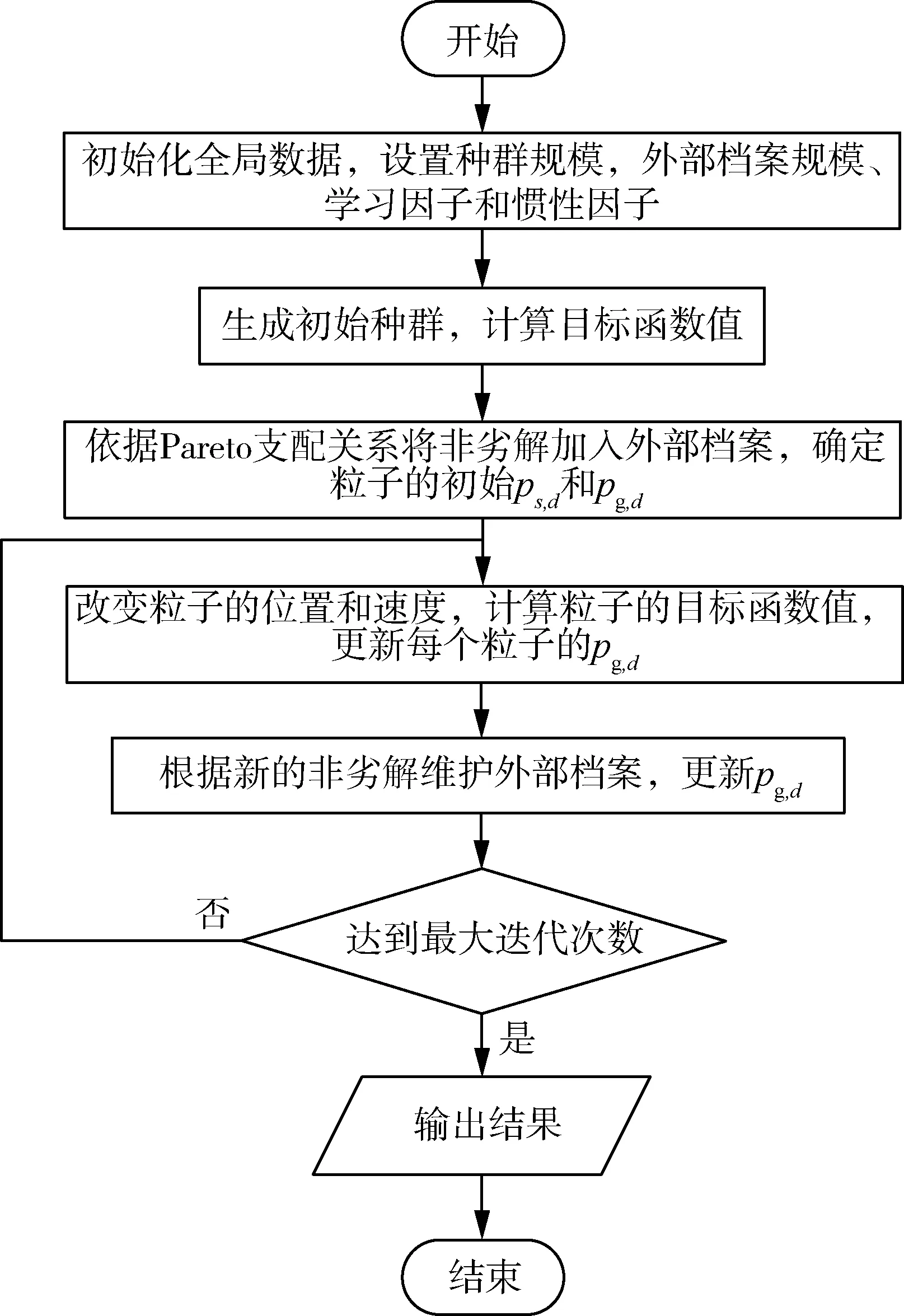
圖1 改進MOPSO算法基本流程圖

2.6 算法測試

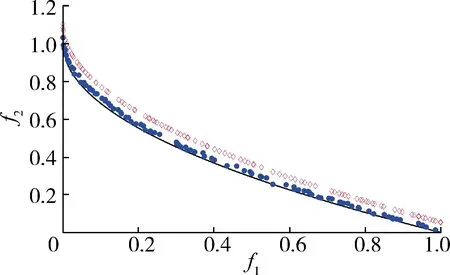
采用ZDT測試函數對改進MOPSO算法進行了測試，選取的ZDT測試函數包括ZDT1、ZDT2、ZDT3和ZDT6[19]。改進MOPSO算法參數的設置為：種群規模為100，外部檔案規模為100，最大迭代次數為5 000，慣性因子和學習因子的選取如前文所示。測試結果與傳統的NSGA-Ⅱ算法求解結果以及真實的Pareto曲線的對比如圖2所示。NSGA-Ⅱ算法采用同樣的種群規模、外部檔案規模、最大迭代次數。

(a) ZDT1

由圖2可知，改進MOPSO算法對測試函數的優化結果均與真實非劣前沿保持一致，所得到的解優于NSGA-Ⅱ算法求解得到的解；從分布性來看，改進MOPSO算法也表現優異，優化結果分布均勻。綜上可見，無論是收斂度還是分布性，改進MOPSO算法在處理多目標問題中均有明顯優勢。

3 實例研究

受黃河沖積影響，宿遷市形成了大面積平原坡水區，地勢上以黃河故道為分水嶺，向南北兩側逐漸傾斜。本文研究范圍位于宿遷市黃河故道以南、南淮泗河以西、市界以東、宿城與泗洪縣界以北，由宿遷市黃河故道流域和黃河故道以南地區組成，涉及宿城區、泗陽縣兩個行政區，總面積1 674.2 km2。

宿遷市黃河故道及以南地區水資源調度系統通過七堡樞紐、運南北渠首等泵站將駱馬湖及中運河的水提到黃河故道，并經由皂河地涵、蔡支閘等11級閘站向下游輸水，同時沿途向運南灌區、船行灌區、皂河灌區和區域內其他用水戶供水，水流最后流入洪澤湖；其中運南灌區還可從洪澤湖提水補充。系統概化圖如圖3所示。

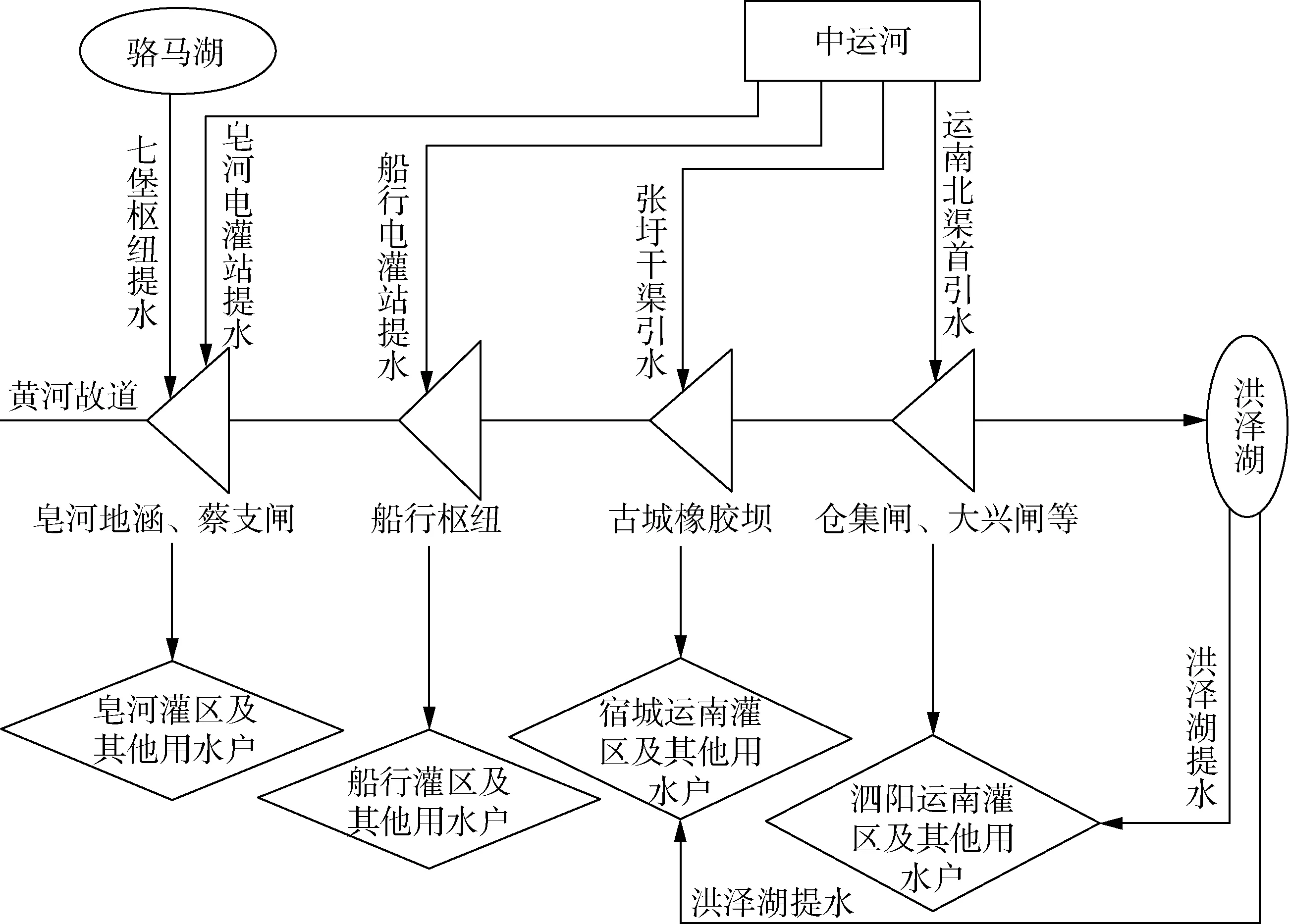
圖3 宿遷市黃河故道及以南地區水資源系統概化圖

宿遷市黃河故道及以南地區水資源優化調度模型包括多水源、多用戶，模型的目標函數和約束條件如前文所述，來水量、需水量、泵站、閘站等的詳細信息限于篇幅不具體列出，最小生態環境流量取河道外生態環境需水量，即保護、修復或建設生態環境需要通過人工供水設施補充的水量，包括城鎮生態環境需水、林草植被建設和濕地保護修復等用水。模型基于2013年(現狀水平年)水資源供需平衡情況，以月為計算時段，以水文年為計算周期，以各區間需水和來水情況為模型輸入，利用改進MOPSO算法對模型進行求解。在50%、75%、95%設計頻率來水條件下用改進MOPSO算法求解調度模型，所得的Pareto前沿如圖4所示。

由圖4可以看出，受水區缺水量與泵站提水量之間呈明顯的負相關關系。若減少泵站提水量，則受水區缺水量增大；反之，若要減少受水區缺水量，則必將以犧牲經濟效益為代價；社會效益與經濟效益之間表現出對立性。對比3種不同頻率來水調度方案可見，當來水量較大時，需要的泵站提水量較小，且受水區缺水量也較小，即兩者之間對立性較弱。總的來說，各頻率來水調度方案集在空間中分布均勻，兩個目標函數值分布范圍較廣，該Pareto前沿可為決策者提供較為全面的決策信息，表明改進MOPSO算法作為一種新的多目標優化問題求解方法，具有較好的可操作性，可有效運用于具體的工程實踐中。

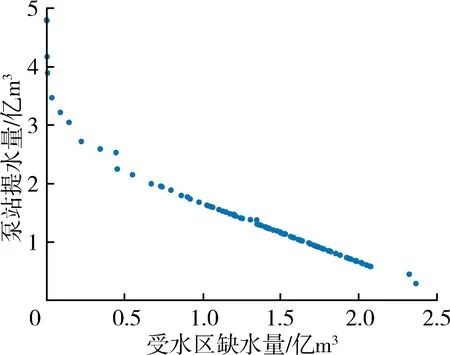
(a) 50%

選取幾種典型調度方案如表1所示，各典型調度方案側重于不同的調度目標。以50%設計頻率為例，方案1為受水區缺水量最小對應的方案，明顯側重于社會效益，這樣不可避免的導致泵站提水量增加，從而影響經濟效益；而方案3則側重于經濟效益，減小泵站提水量從而降低提水成本，但其缺水率接近50%，忽視了區域用戶的用水需求，違背了社會目標；方案2為最佳均衡解，其缺水率為10%左右，但提水量僅為方案1的一半，因此可以看作是方案1和方案3的折中。可見切合實際的調度方案需要權衡社會效益和經濟效益，在實際應用中，決策者可根據實際需要進行多屬性決策從而選定適當的調度方案。

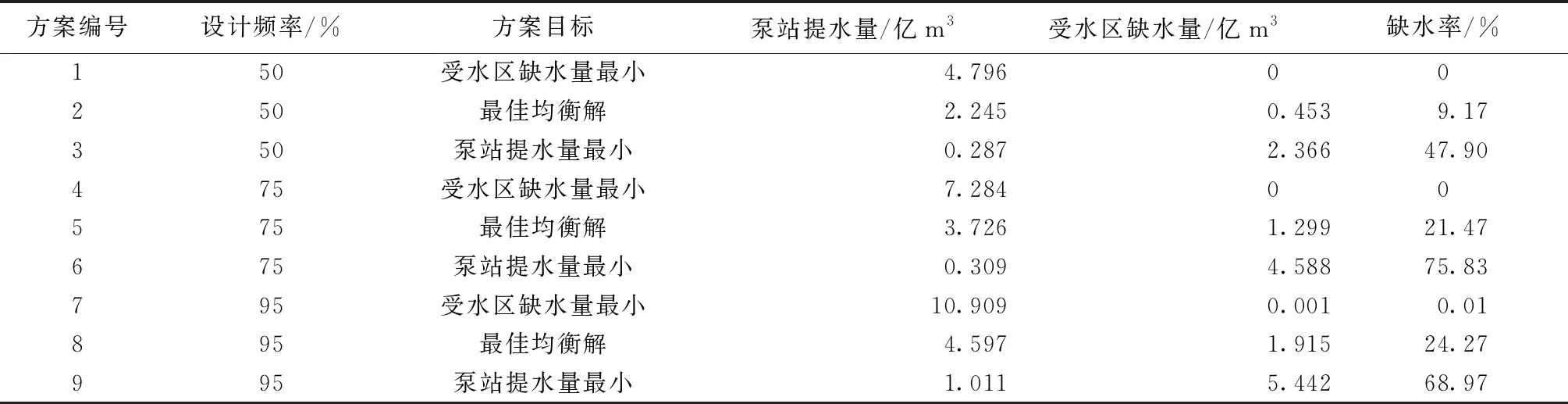
表1 50%、75%、95%設計頻率下典型調度方案集

4 結 語

本文針對平原坡水區水資源優化調度的特點建立了相應的數學模型。根據粒子群算法基本理論，從慣性因子及學習因子選擇、外部檔案維護和全局最優選取策略3個方面進行改進，并對比改進算法與傳統的NSGA-Ⅱ算法在求解測試函數中的表現，驗證了改進MOPSO算法在處理多目標問題上的良好性能。對宿遷市黃河故道及以南地區水資源優化調度進行了實例研究，采用改進MOPSO算法求解模型得到Pareto前沿。結果顯示，兩個目標函數值分布范圍較廣，且各頻率來水調度方案集在空間中分布均勻，表明改進MOPSO算法是一種解決多目標約束和復雜非線性系統問題的有效優化方法。