分數階Like-Bao系統自適應滑模同步的整數階滑模面設計
周長芹,毛北行,王東曉
(鄭州航空工業管理學院數學學院,河南 鄭州 450015)
0 引言
混沌系統具有對初始條件及參數變化的敏感性,因而備受人們關注,其在保密通訊、信號與處理、經濟學、物理學及控制學科等領域被廣為應用.伴隨著分數階微積分這一學科的發展,越來越多的科研人員逐漸關注到此類同步控制并把該問題作為研究的熱點[1-3].文獻[4]進行了分數階Duffling系統混沌終端滑模同步問題的研究;文獻[5]對分數階Genesio-Tesi系統的適應轉移滑模同步問題進行了研究;文獻[6]運用了兩種不同的滑模方法,對分數階Newton-Leipnik系統的同步問題進行了探討;文獻[7]給出分數階比例積分滑模面的設計與構造;文獻[8]研究了一類神經網絡系統的有限時間同步;文獻[9]對一類分數階時滯神經網絡系統的有限時間同步問題進行了研究與分析.同時,很多專家學者對Like-Bao系統的同步控制進行了研究.文獻[10]基于比例積分滑模方法,對分數階超混沌Bao系統同步進行了研究;文獻[11]給出了超混沌Like-Bao系統的混沌運動及動力學分析方面的研究結果;文獻[12]探討了一類超混沌Bao混沌系統的線性反饋同步問題.本文構造了新的整數階滑模函數以及自適應規則,對分數階Like-Bao混沌系統滑模同步問題進行了研究,得到分數階Like-Bao混沌系統自適應滑模同步的充分條件.
1 系統描述和主要研究結果
定義1[13]Caputo分數階導數的定義為

分數階Like-Bao系統描述為[14]
(1)
當a=38,b=6,c=20,k=2,q=0.896時,吸引子如圖1所示.
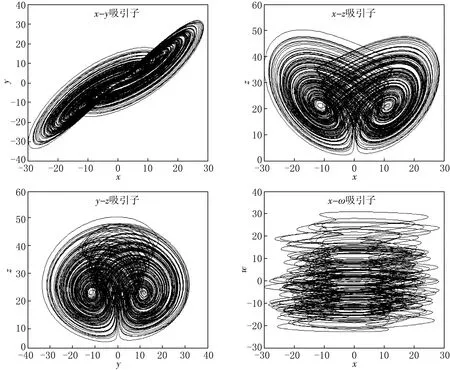
圖1 系統吸引子
設計從系統如下:
(2)
其中:φ(t)=[x1,y1,z1,ω1]T,Δfi(φ(t))為有界不確定項,di(t)為有界外擾.定義e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,從而有
(3)
假設1 存在未知常量mi,ni(mi,ni>0),滿足|Δfi(φ(t))|≤mi,|di(t)|≤ni.
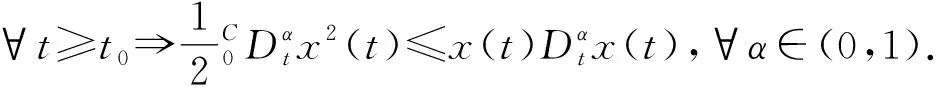
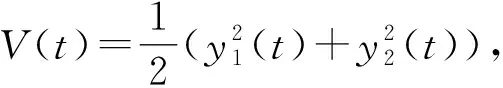
定理1 構造滑模面si(t)=ei,控制輸入為
自適應規則為
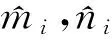
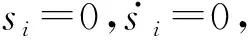
因為si(t)=ei,故
整數階Like-Bao混沌系統可描述為
(4)
從系統設計為
(5)
其中:φ(t)=[x1,y1,z1,ω1]T,Δfi(φ(t))為有界不確定項,di(t)為有界外擾.定義e1=x1-x,e2=y1-y,e3=z1-z,e4=ω1-ω,從而有
(6)
定理2 構造滑模面si(t)=ei,控制輸入
自適應規則為
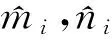
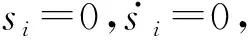
由于si(t)=ei,故
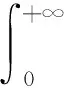
兩邊積分得
由引理3得到si(t)→0,從而ei(t)→0.
2 數值仿真
定理1與定理2的誤差分別見圖2與圖3.通過觀察可得,初始時誤差較大,與原點的距離遠,但隨后誤差曲線距離原點越來越近并且逐漸趨于一致.
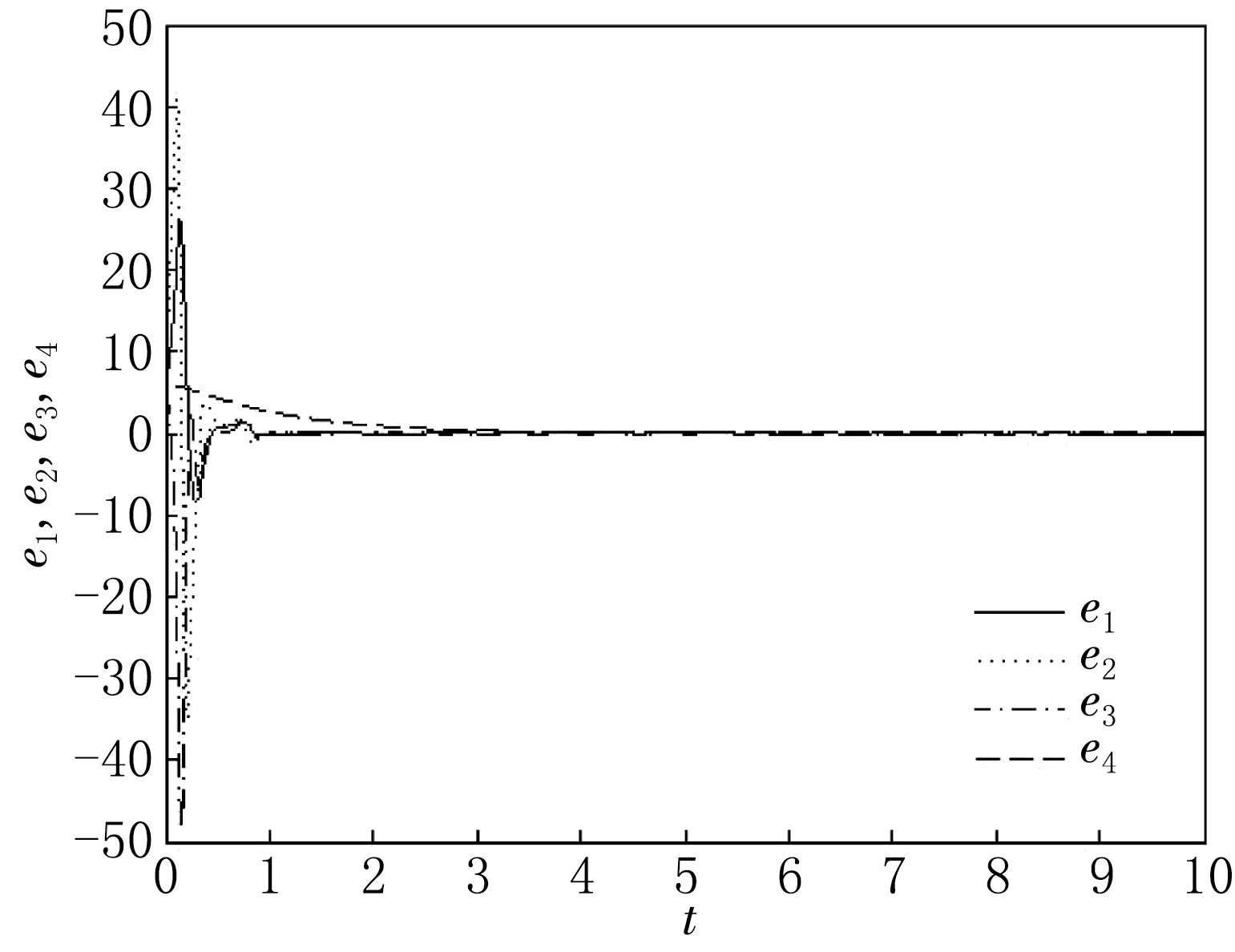
圖2 定理1的系統誤差
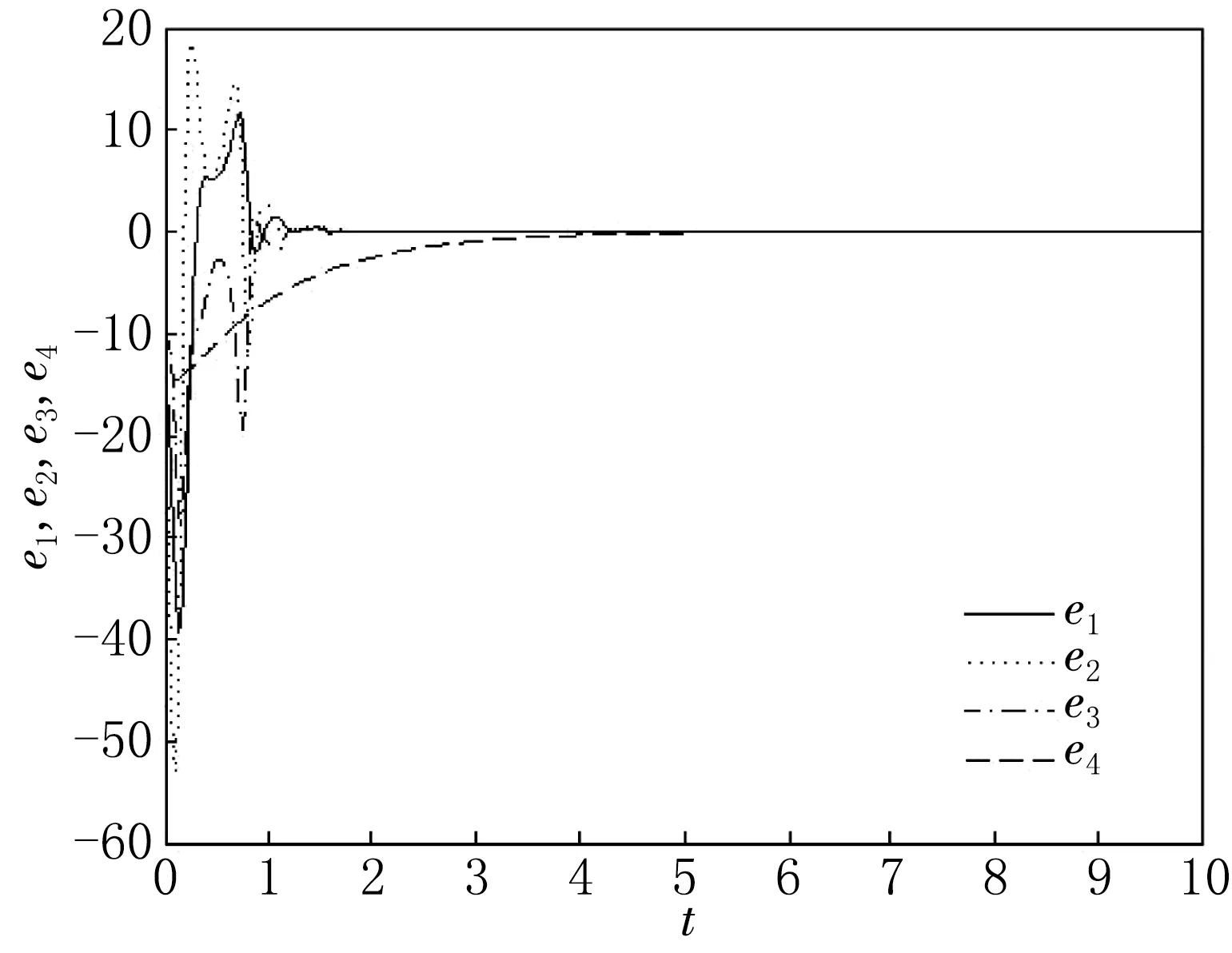
圖3 定理2的系統誤差
3 結論
通過構造一種整數階滑模函數和自適應控制規則,對不確定分數階Like-Bao系統的自適應滑模同步問題進行了研究,得出了系統取得自適應滑模同步的兩個充分條件.結論說明在滿足一定條件的前提下,不確定分數階Like-Bao混沌系統的主從系統可取得自適應滑模同步.MATLAB仿真技術也驗證了這一結論.

