一類潛伏期與染病期均具有傳染性的隨機傳染病模型

胡 瑞，黃立冬，李榮庭，徐權峰

(云南民族大學 數學與計算機科學學院，云南 昆明 650500)

自古以來，傳染病一直阻礙著人類社會的發展，所以基于傳染病的研究一直被學術界廣泛關注.為了更加深入了解傳染病，避免其對社會和經濟的危害，學者們通過建立微分方程模型對傳染病進行定性分析和定量研究.20世紀初，Kermack和Mekendrick提出了最經典的傳染病模型SIR(susceptible-infection-removed)倉室模型[1-2].此后傳染病動力學的建模和研究開始快速發展[3-11].但是，在現實生活中，由于環境多變，確定性的傳染病模型很難做到對實際情況的具體描述.1951年，KiyoshiIt引入了It微積分對隨機現象的研究和分析.經過學者們不斷的深入研究，隨機微分方程取得了很大的進展.因此隨機微分方程也被引入到疾病動力學領域中.近年來，國內外學者在基于隨機擾動的傳染病模型的研究中取得了很多成果[12-17].

胡晶晶[18]建立了幾類隨機SIQS傳染病模型，通過構造Lyapunov函數、使用It公式以及強大數定理等證明傳染病模型存在全局唯一正解.通過得出的疾病滅絕充分條件，結果表明大的噪聲可以抑制疾病的爆發.徐敏等[19]考慮傳染病傳播過程中的隨機干擾，運用隨機人口建模中參數擾動的標準化技術，建立了一類具有隨機擾動的傳染病SEIR模型.李雪等[20]建立了一類隨機SEIQR傳染病模型，通過構造合適的Lyapunov函數并利用It公式，證明了該傳染病模型的全局唯一正解的存在性，通過確定性SEIQR模型進而研究隨機模型的漸近行為.

而在現實生活中，部分傳染病在潛伏期同樣具有傳染性.如2019年末爆發的COVID-19.由于其潛伏期具有傳染性，短時間內病毒席卷全球，造成很大的損失.綜上所述，在現有傳染病模型中加入隨機擾動對疾病傳播的影響，建立一類潛伏期和染病期均具有傳染性的隨機SEIQR模型更加具有實際意義.

1 模型建立

本文研究的是一類隨機SEIQR模型，在此之前首先建立一類確定性SEIQR模型，模型將人口分為易感者(S)，潛伏者(E)，隔離者(Q)，感染者(I)以及恢復者(R)5個部分，并建立以下模型

(1)

其中,A表示易感者的常數輸入率，d表示自然死亡率，δ1,δ2,δ3分別表示潛伏者，染病者和隔離者的康復率，β1表示潛伏者與易感者之間的有效接觸率，β2表示染病者與易感者之間的有效接觸率，ε表示潛伏者轉為染病者的比率，α表示染病者的因病死亡率，γ表示隔離者的因病死亡率，μ1表示潛伏者被隔離的比率，μ2表示染病者被隔離的比率，從生物數學角度考慮，規定本文所有參數都是非負的.該模型對應的流程圖如下：

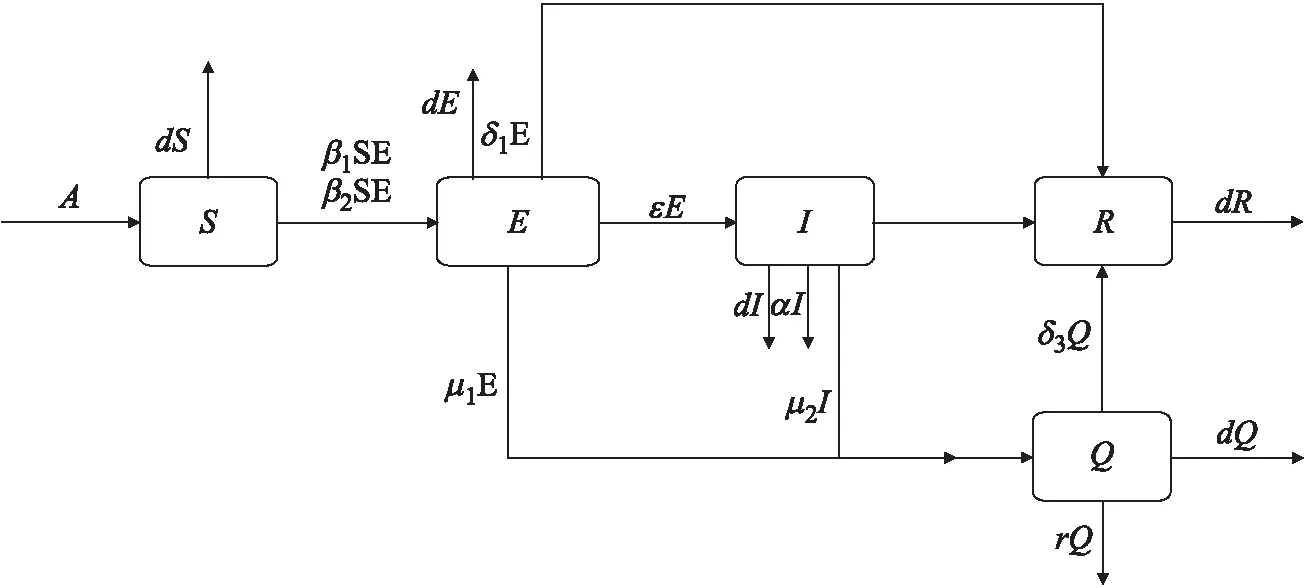
圖1 確定性SEIQR模型流程圖

本模型的基本再生數為

當R0≤1時,系統(1)無病平衡點P0為(A/d,0,0,0,0)；當R0>1時，有唯一地方病平衡點P*=(S*,E*,I*,Q*,R*)，均全局漸近穩定[21].

設Bi(t)(i=1,2,3,4,5)為獨立的一維布朗運動，σi(i=1,2,3,4,5)為噪聲強度，建立一類潛伏期與染病期均具有傳染性的隨機SEIQR傳染病模型，對應的微分方程組為

(2)

2 全局正解的存在唯一性

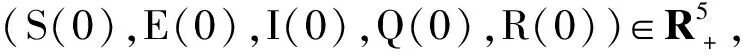
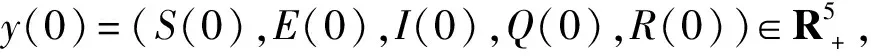
取充分大的正數k0≥0，使得初值y(0)的每一個分量都屬于區間[1/k0,k0]，對?k≥k0，k∈N+整數，定義停時

這里inf?=∞(?表示空集).

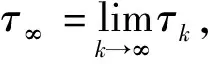
若τ∞=∞a.s.成立，則有τk=∞a.s..采用反證法，證明如下：

如若不然，存在常數T>0和δ∈(0,1)使得P{τ∞≤T}>δ.因此，存在整數k1>k0，?k≥k1，都有P{τk≤T}≥δ.

構造lyapunov函數，得

V(y)=(S+1-lnS)+(E+1-lnE)+(I+1-lnI)+(Q+1-lnQ)+(R+1-lnR).

dV=LVdt+(S-1)σ1dB1(t)+(E-1)σ2dB2(t)+(I-1)σ3dB3(t)+

(Q-1)σ4dB4(t)+(R-1)σ5dB5(t),

其中,

得

取

則有

dV≤Kdt+(S-1)σ1dB1(t)+(E-1)σ2dB2(t)+(I-1)σ3dB3(t)+

(Q-1)σ4dB4(t)+(R-1)σ5dB5(t).

對于上式，從0到τk∧T積分，并取期望有

EV(S(τk∧T),E(τk∧T),I(τk∧T),Q(τk∧T),R(τk∧T))≤V(y(0))+KT.

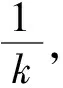
得

其中1Ωk表示Ωk的示性函數.

令k→∞，有∞>V(y(0))+KT=∞，矛盾.于是必有τ∞=∞a.s.即解是正的且全局唯一存在.

3 模型解的漸近行為

當確定性SEIQR傳染病模型的R0≤1時，模型(1)存在無病平衡點P0=(A/d,0,0,0,0)且全局穩定.接下來，討論模型(2)的解在P0點附近的漸近性質.

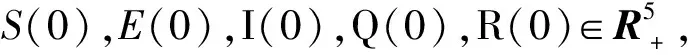
若滿足條件

其中

證明構造lyapunov函數

顯然，V1,V2,V3,V4,V5,V6是正定的，由It公式計算得

當R0≤1，使得：

又2ab≤a2+b2，有

構造Lyapunov函數

顯然V正定，由It公式計算可得

其中

從0到t取積分并取期望，有

若滿足

則有

證明完畢.

由定理2可知，當確定性傳染病模型(1)的R0≤1時，模型(2)的解會在確定性SEIQR模型無病平衡點P0附近擾動，且波動大小與σ1有關，當環境噪聲強度越小時，模型(2)的解越趨近于模型(1)無病平衡點P0.

當確定性傳染病模型(1)的R0>1時，存在唯一的地方病平衡點P*=(S*,E*,I*,Q*,R*)且全局漸近穩定，接下來，討論模型(2)的解在P*點附近的漸近性質.

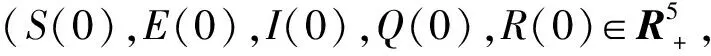
若滿足條件：

其中

證明構造lyapunov函數

顯然V1,V2,V3,V4,V5正定，由It公式，計算得

dV1=LV1dt+(S-S*+E-E*)(σ1SdB1(t)-σ2EdB2(t)),

其中

(3)

當R0>1時，確定性SEIQR模型(1)有唯一地方病平衡點P*=(S*,E*,I*,Q*,R*).令確定性SEIQR模型左邊等于零，得

A=β1S*E*+β2S*I*+dS*,

β1S*E*+β2S*I*=(d+ε+δ1+μ1)E*,

εE*=(d+α+δ2+μ2)I*,

μ1E*+μ2I*=(d+γ+δ3)Q*,

dR*=δ1E*+δ2I*+δ3Q*.

將上述等式帶入(3)中，得

同理得出

得出不等式

通過構造Lyapunov函數

V=V1+V2+V3+V4.

dV=LVdt+(S-S*+E-E*)Sσ1dB1(t)+Eσ2dB2(t)+(I-I*)Iσ3dB3(t)+

(Q-Q*)Qσ4dB4(t)+(R-R*)Rσ5dB5(t).

(4)

令

有

LV≤m1(S-S*)2+m2(E-E*)2+m3(I-I*)2+m4(Q-Q*)2+m5(R-R*)2+K.

對(4)取期望，計算得：

那么，當

0

有：

由定理3可知，當模型(1)的R0>1時，模型(2)的解在確定性SEIQR模型唯一的地方病平衡點P*擾動，且波動范圍與σ1,σ2,σ3,σ4,σ5有關，當環境噪聲強度越小時，模型(2)的解越接近地方病平衡點P*，并在P*附近波動.