基于RNG k-ε湍流模型的串列雙矩形截面橋墩繞流流場特性研究

丁安娜

(鉛山縣水利局，江西 上饒 334599)

隨著中國經濟和交通運輸行業的快速發展，越來越多的跨江、跨海橋梁被修建，對江河兩岸人員通行、文化交流和物資運輸等起到了重要作用[1-2]。據統計，截至2019年中國公路大型橋梁數量多達10.8萬座，對推動區域經濟發展起著顯著作用[3]。然而，涉河橋梁的建設將影響河流的度汛安全，對橋墩周圍流體流動、河床阻力及船舶航行等造成不利影響[4]。《中華人民共和國防洪法》規定，涉河項目建設應符合防洪標準，不得危害堤防安全、影響河勢穩定、妨礙行洪暢通等相關內容[5-6]。因此，研究橋墩繞流流場結構特征對優化橋墩布設、保障船舶安全航行等具有重要意義。

大量學者對橋墩繞流開展了大量物理實驗與數值模擬等研究。葉玉康等[7]開展了串列雙圓柱橋墩繞流流場特性的數值模擬研究，分析了不同橋墩間距對橋墩周圍渦量分布和橫向流速的影響。田正野等[8]采用大渦模擬分析了串列多圓柱橋墩繞流特征，獲得了圓柱橋墩繞流的壓力云圖、瞬時流速和渦量圖等。童曉劍[9]開展了低雷諾數條件下多圓柱橋墩繞流流動特性，分析了橋墩排列方式、間距和直徑比對圓柱橋墩繞流流動特性的影響。余攀登等[10]以海底懸跨管道為研究背景，分析了高雷諾數下近壁圓柱的繞流特征。高鵬程等[11]研究了圓端形橋墩周圍流體的行進水流及其流場變化，探索了圓端形橋墩繞流與沖刷之間的關系。此外，李鶴高、魏彭林等[12-13]對橋墩周圍紊流區寬度進行了研究。綜上，目前大部分學者主要研究的是單橋墩繞流，尤其是圓柱繞流，有少數學者對多圓柱橋墩繞流進行了研究。據有關學者對長江流域上89座橋梁橋墩截面形狀的統計結果，水中無橋墩和為斜拉橋異形墩分別占23%、41%，圓端形截面墩、矩形截面墩和圓形截面墩分別占10%、11%、3%[14]。矩形截面橋墩因采用現澆和模板拼裝施工，施工速度快，從而在橋梁工程中被廣泛采用。因此，本文以多矩形截面橋墩實際工程為研究背景，采用Fluent軟件對單矩形截面橋墩和串列雙矩形截面橋墩繞流流場進行數值模擬計算，分析不同橋墩間距工況下串列雙矩形橋墩繞流流場分布特征。

1 數值計算模型

a)模型的建立。以忠州長江大橋為實例建立模型，該橋梁橋墩采用矩形薄壁空心墩，截面尺寸為6 000 mm×4 000 mm，屬于中等尺度橋墩。為提高模型計算速度，采用1∶50縮尺比進行模型建立，縮尺后矩形橋墩尺寸(長和寬分別用H、W表示為：H×W=120 mm×80 mm。圖1所示，整個模型計算域尺寸為：40W×20W，即3 200 mm×1 600 mm，橋墩前側為流體入口，后側為出口。為充分研究水流經過不同間距橋墩后的流動特征，第一個橋墩中心距流體入口10W，距流體出口30W；順著水流流動方法看，定義橋墩的左側區域和右側區域分別為橋墩左側和右側，且橋墩中心距兩側邊界均為10W。

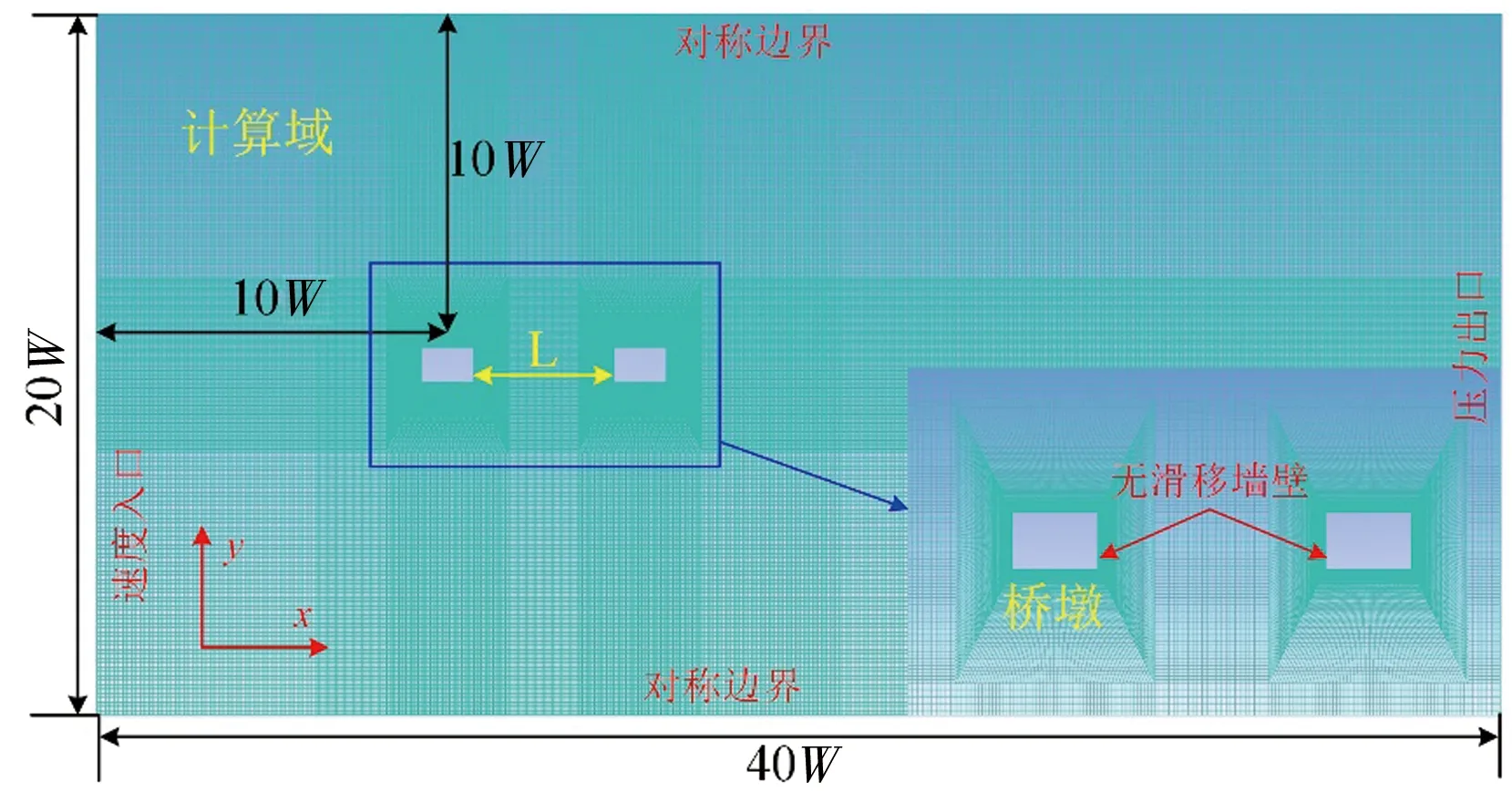
圖1 數值計算模型網格劃分

b)計算工況。數值模擬重點研究流體繞橋墩流動狀況，流體經過橋墩后流向發生改變，流線會出現嚴重彎曲。因此，控制方程采用重整化的RNG k-?雙方程湍流模型，該模型在求解高彎曲程度和高應變率的流體流動時具有更高的計算精度、更好的求解穩定性和更快的求解速度等，大量學者已采用該模型求解橋墩繞流問題[3,15-17]。數值計算控制方程的具體參數參照葉玉康等[7]的研究成果。計算域入口流體流速設定為恒值，其大小為0.4 m/s，方向沿x軸正向。論文研究重點是不同間距矩形截面橋墩繞流的流場特性，因此橋墩間距L設置了L/W=0、2、4和6四種工況，其中間距L是指第二個橋墩前壁至第一個橋墩后壁的距離，L/W=0是指單個矩形截面橋墩繞流工況。

c)計算網格和邊界條件。圖1所示，模型利用ICEM軟件進行結構化四邊形網格劃分。為更好捕捉橋墩周圍繞流流場細節，尤其是尾流流場特性，對計算域橋墩中心線附近區域進行了局部加密細化處理；此外，為提高計算精度，對橋墩周圍網格進行進一步加密處理，計算模型網格總數量約為9.2萬。模型邊界條件設置如下：計算域前側設置為速度入口，為0.4 m/s；后側設置為壓力出口，為101 000 Pa；橋墩壁為無滑移壁面，計算域左右兩側邊界設置為對稱邊界。模型采用非穩態瞬時計算方法，總計算時間為30 s。

2 串列雙矩形截面橋墩繞流流場特性

2.1 矩形截面橋墩與常規圓柱形橋墩繞流流場對比分析

圖2顯示了矩形截面橋墩繞流特征與常規圓柱橋墩的對比結果。圓柱橋墩繞流結果為葉玉康等[7]開展的雙圓柱橋墩數值模擬結果。由圖可知，在兩橋墩間距相近條件下，矩形截面橋墩繞流流動更復雜，其橋墩尾流渦體尺寸更大，渦體及流線彎曲區橫向分布范圍更廣；從橫向流速時程曲線分布可知，圓柱橋墩繞流橫向流速波形圖形態單一且呈對稱分布，但矩形橋墩繞流橫向流速波形圖周期內出現局部波動，波形圖形態復雜，且橫向流速峰值更大。總體而言，矩形截面橋墩因其排導性差，對來流干擾程度大，較常規圓柱橋墩繞流運動更復雜。因此，十分有必要研究矩形截面橋墩布置參數對其繞流流場特征的影響。

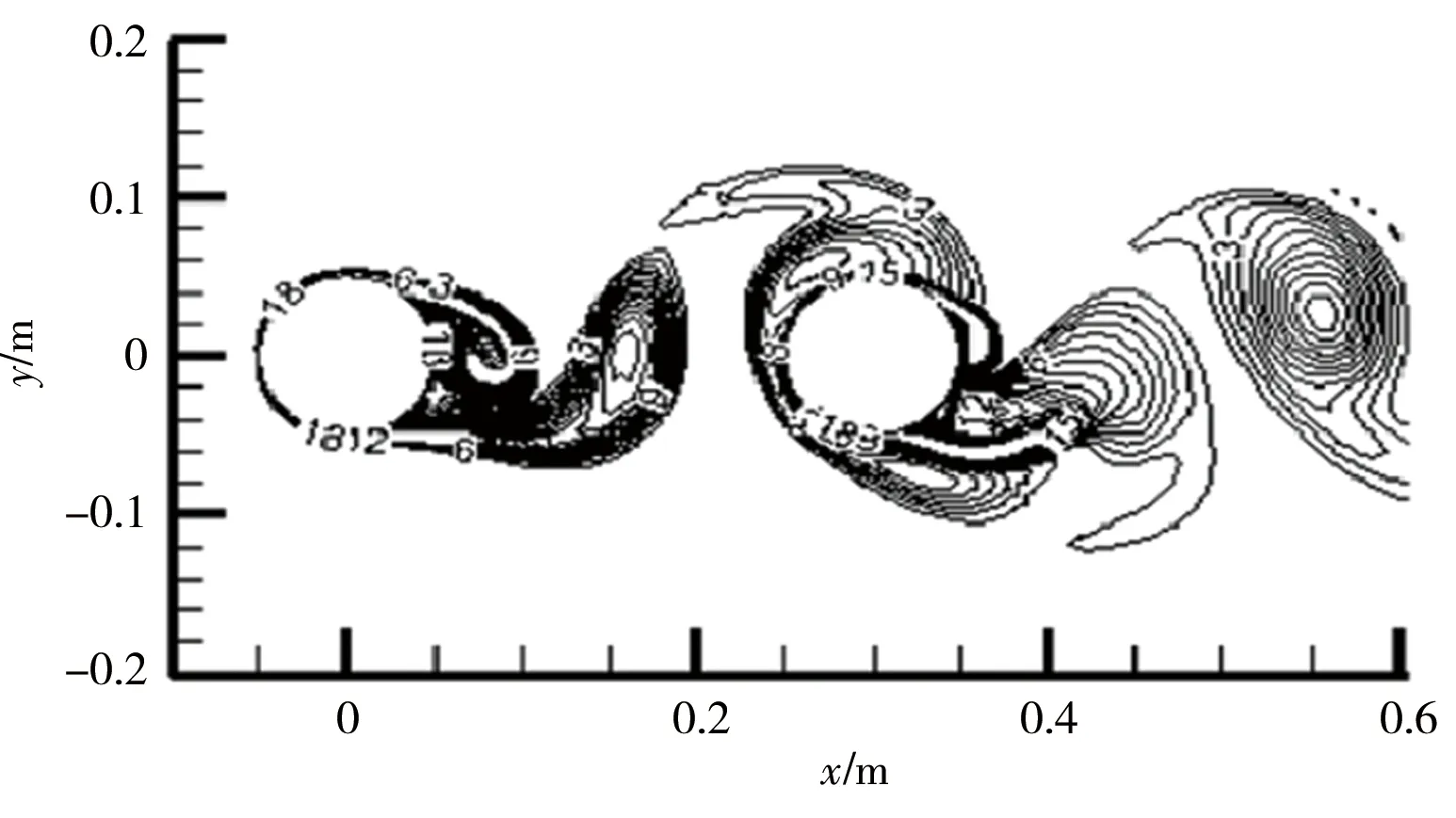
a)圓柱橋墩渦量等值線

2.2 渦量分布

圖3顯示了不同間距條件下矩形截面橋墩尾流渦量等值線。由圖可知，與單矩形截面橋墩繞流相比，串列雙矩形截面橋墩尾流流動更加復雜，且流動狀態與橋墩間距緊密相關。當L/W=0時，即單橋墩工況，流體經過矩形截面橋墩后，其尾流出現了卡門渦街現象，并在距橋墩不同距離下游處形成了多個渦體，渦體形態、尺寸等分布具有較強的規律性。對串列雙矩形截面橋墩而言，當L/W=2時，尾流的渦量等值線分布較單矩形橋墩更為復雜，但由于兩橋墩間的距離不足以讓渦體在兩橋墩間充分發展，渦體只在第二個橋墩尾流中形成。圖3b所示，第一個橋墩SL1側剪切層分離后重附在第二個橋墩剪切層上，而SL2側剪切層將直接摻混到第二個橋墩尾流旋渦中；此外，串列雙矩形截面橋墩尾流旋渦的橫向分布范圍也將明顯擴大，單橋墩和串列雙矩形橋墩渦體橫向分布范圍分別為5.6W、8.0W。當L/W≥4時，第一個矩形橋墩兩側剪切層不再附著在第二個橋墩剪切層上，每個橋墩后尾流都會形成卡門渦街，并在第一個矩形橋墩尾流旋渦干擾下，第二個矩形橋段尾流流動變得更加不穩定，渦體之間相互附著，渦量強度也隨之增大，渦量等值線分布密度加密。

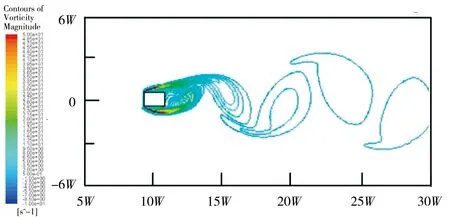
a)L/W=0

2.3 流線及壓力分布

圖4為t=30 s時不同間距條件下矩形截面橋墩繞流流線分布。流體在橋墩前方區域流動十分穩定，流體流速幾乎相同，且流線之間相互平行(圖4中紅色箭頭所示)。當流體經過矩形截面橋墩時，橋墩迎面流體將從兩側繞行，橋墩前壁流體流線將嚴重彎曲，流體流向發生改變。橋墩使流體過流斷面積減小，在橋墩兩側的流體流速將增加(如橋墩兩側紅色流線區域)，且流線分布更密。橋墩尾流由于渦體的產生，在渦體區域流體流線將嚴重翻轉和彎曲，且流體流速較低，為低速區(如橋墩尾流綠色流線分布區域)。由圖4可知，矩形截面橋墩間距對流線分布具有重要影響。單矩形截面橋墩繞流流線分布和常規圓柱形橋墩繞流情況類似(圖4a)。當橋墩間距L/W≤2時(圖4b)，第一個橋墩尾流彎曲的流線與第二個橋墩相遇，從橋墩兩側繞流，并在兩側形成速度增加區域；第二個橋墩尾流流線分布與單橋墩尾流流線分布類似，但流線彎曲程度更嚴重，且彎曲流線的橫向分布區域更廣。當橋墩間距L/W≥4時(圖4c—4d))，兩橋墩間也將出現流線彎曲區域，其余流線分布特征與L/W≤2時較為類似。

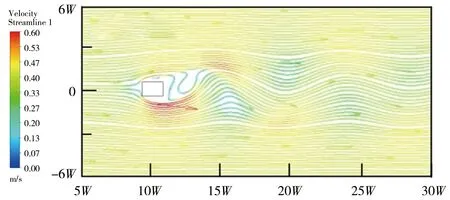
a)L/W=0

在t=30 s時，不同間距串列雙矩形截面橋墩繞流壓力分布見圖5。在第一個矩形截面橋墩前形成了壓力增高區(紅色區域)，而橋墩兩側和后方為壓力降低區(綠色和藍色區域)。結合圖4可知，其主要原因為：根據伯努利方程，由于橋墩使流體過流面積縮小，橋墩前方流體形成駐流，流速降低且流向發生改變，且兩側流速增加，從而在橋墩前方和其他方向分別形成壓力增加區和壓力降低區。此外，串列雙矩形截面橋墩尾流流動更加復雜，低壓區分布范圍更廣，且流動狀態與橋墩間距緊密相關。當橋墩間距L/W≤2時，兩橋墩間全為壓力降低區，第二個橋墩尾流形成了多個壓力降低區。當橋墩間距L/W≥4時，在第一個橋墩后方除形成壓力降低區外，在第二個橋墩前方還形成了局部壓力增高區，但壓力值較第一個橋墩前方更小。

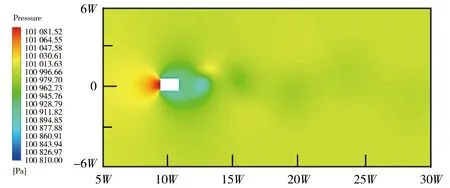
a)L/W=0

2.4 橫向流速分布

由橋墩繞流流線及壓力分布云圖可知，流體在橋墩前方的計算域內沿x軸正向流動，當遇到橋墩時，橋墩壁前方形成駐流，隨后沿橋墩兩側分離流動，并在橋墩后方匯流。因此，橋墩繞流將形成斜向流動，定義垂直于兩橋墩中心線方向的流體流速為橫向流速。圖6顯示了不同間距串列雙矩形截面橋墩繞流橫向流線分布云圖，橋墩間距分別為L/W=0，2，4，6。由圖6可知，第一個矩形截面橋墩前方兩側形成了對稱分布的正負橫向流速區。對單橋墩繞流而言(即L/W=0)，橋墩后方尾流橫向流速在不同距離處呈正負交替分布(圖6中黃色和藍色區域)，主要是由橋墩尾流交替分布的渦體不斷生成、發展和潰滅所導致。對串列雙矩形截面橋墩而言，兩橋墩之間區域會出現正負橫向流速區，且間距越小橫向流速值越大，但正負橫向流速分布區隨著間距的增加而增多。第二個矩形橋墩尾流橫向流速分布規律與單橋墩較為類似，但串列雙矩形截面橋墩繞流的正負橫向流速值更高，且橫向分布區范圍更廣。

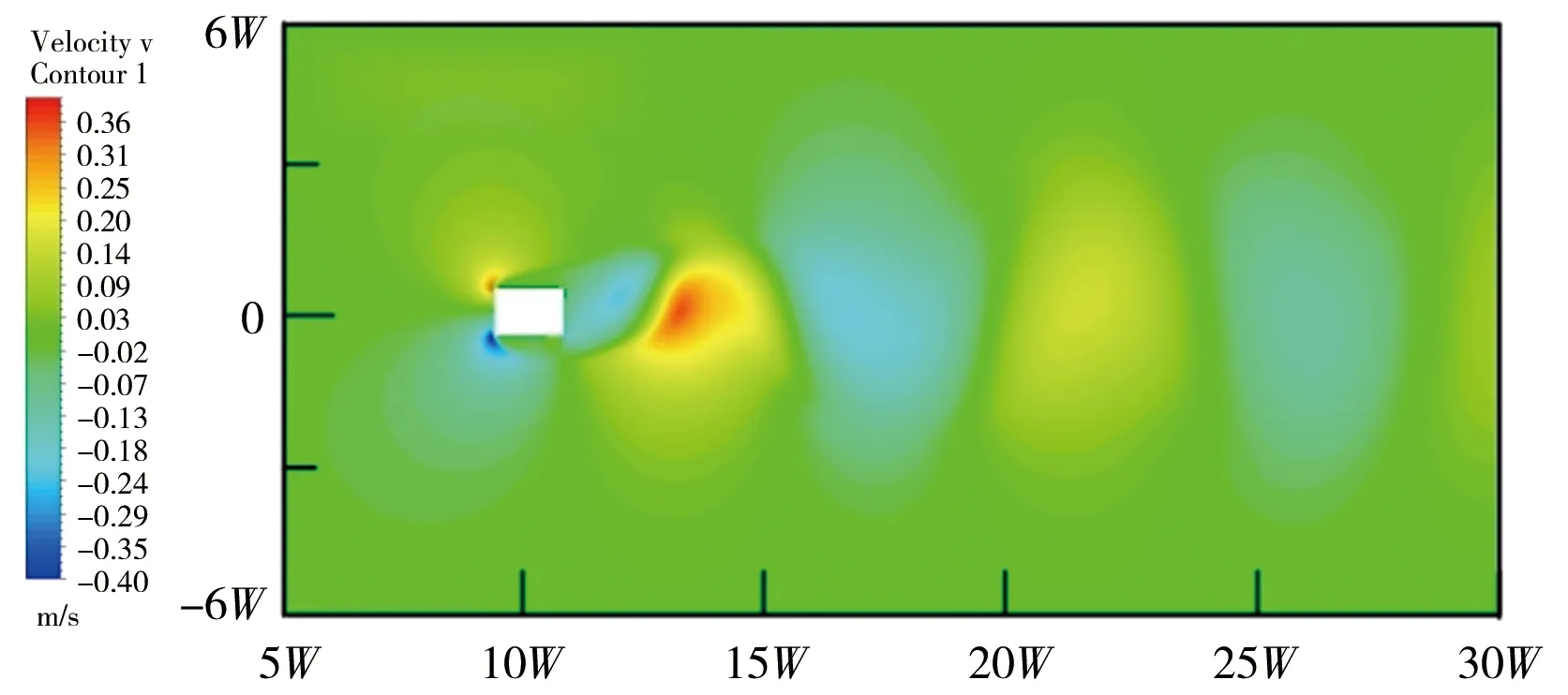
a)L/W=0

橋墩繞流橫向流速分布規律與船舶航行狀態密切相關。為更好揭示橋墩繞流不同位置的橫向流速分布規律，對橋墩周圍不同時刻流體的橫向流速進行觀察，各觀察點位置見圖7。觀察點a—h號位于距橋墩中心線1.25W測線上，其中b號點位于過第一個矩形橋墩中心的垂線上，其前方距離W處為a號點，后方按間距W和2W依次設置c—h號點；i、j號測點在b號上方，距橋墩中心線距離分別為2W、3W；o、p號測點在h號上方，距橋墩中心線距離分別為2W和3W。

圖7 串列雙矩形截面橋墩橫向流速觀察點位置

圖8所示，從不同間距橋墩繞流在y=1.25W測線上各代表性測點(橋墩上游測點a號、第一個橋墩左側測點b號、兩橋墩間測點c、d號、橋墩下游測點g、h號)橫向流速的時程曲線可知，各測點橫向流速均出現周期性波動。第一個矩形橋墩左前方區域橫向流速均為正值，如測點a、b號，且橫向流速曲線波形呈對稱分布。對單矩形截面橋墩而言(即L/W=0)，橋墩后方區域橫向流速都在vy=0 m/s上下波動，波動范圍為-0.2～0.2 m/s，且橫向流速波形圖為對稱分布。對串列雙矩形截面橋墩而言，第一個橋墩后方區域橫向流速正負交替變化，且2個橋墩之間左側區域橫向流速正峰值略大于負峰值；第二個橋墩后方區域橫向流速波形圖不再對稱，在曲線某一位置出現二次波動，這主要由第一個橋墩尾流渦體對第二個橋墩的沖擊和干擾，以及第二個橋墩尾流渦體的脫落導致。此外，橋墩尾流橫向流速波動峰值較單橋墩有所提高，尤其是正峰值，大部分達到了0.3 m/s，尤其是L/W=2工況中的d號測點，該點恰好位于第二橋墩左側附近，該區域流體橫向流速明顯增加，正峰值達到0.5 m/s。

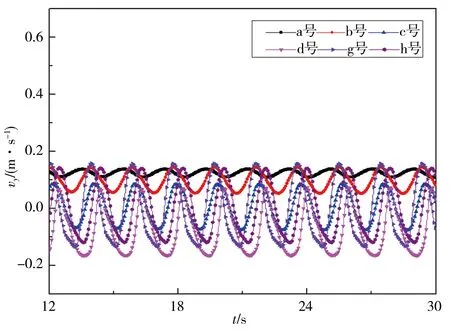
a)L/W=0

圖9、10為距橋墩中心線不同距離處測點橫向流速變化曲線，其中測點b、i、j號位于第一個橋墩左側，測點h、o、p號位于第二個橋墩左后方。對單矩形橋墩和串列雙矩形橋墩而言，b、i、j號測點橫向流速波形圖單一且對稱分布，但串列雙矩形橋墩繞流橫向流速峰值更大；距離橋墩越遠，測點橫向流速波動峰值越小。對第二個橋墩左后方區域，橫向流速波形圖變得不對稱，尤其對L/W=6工況而言，h、o、p號測點橫向流速不再周期變化。總體上而言，距離橋墩中心線越遠，橫向流速越低。

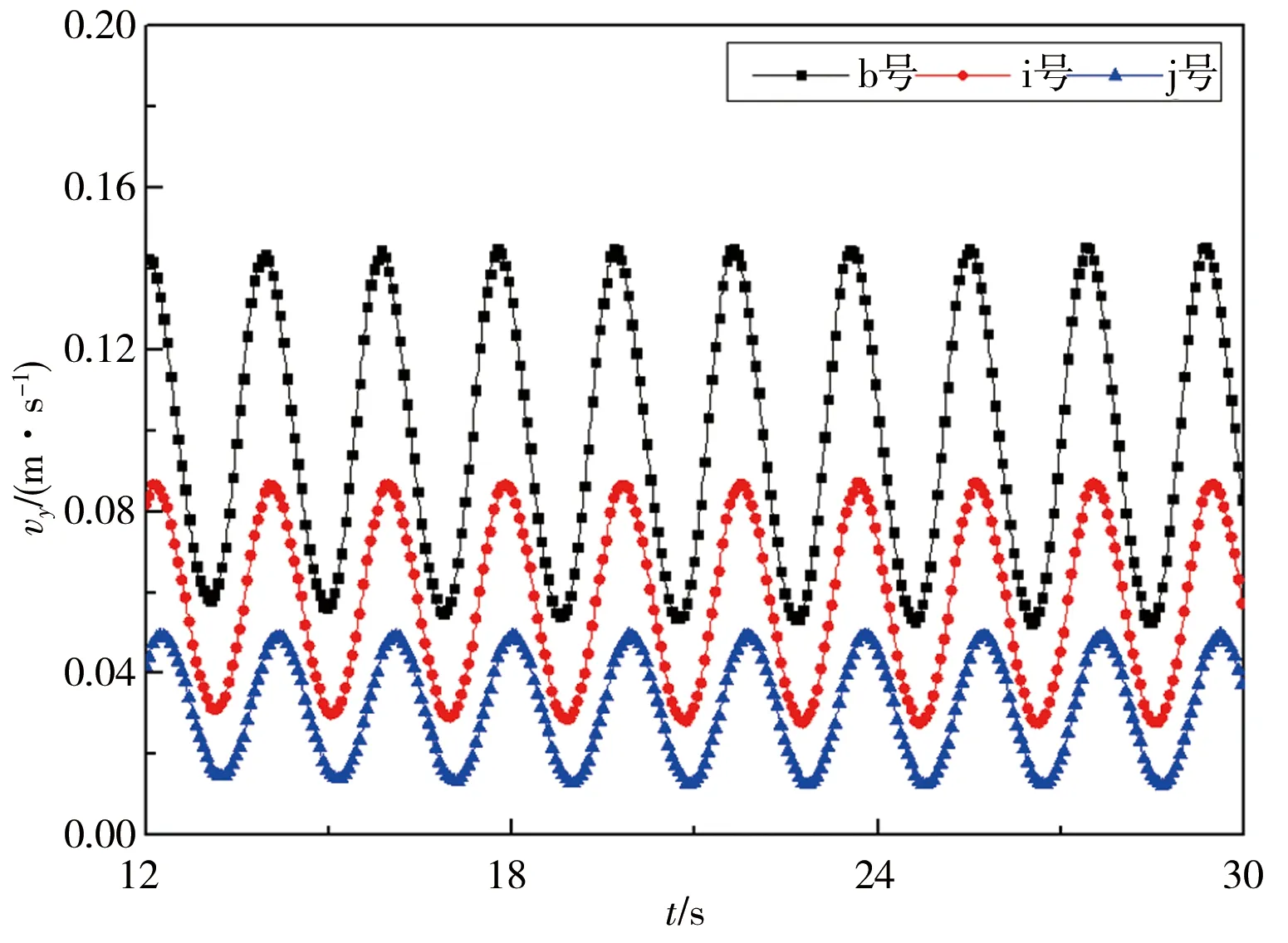
a)L/W=0

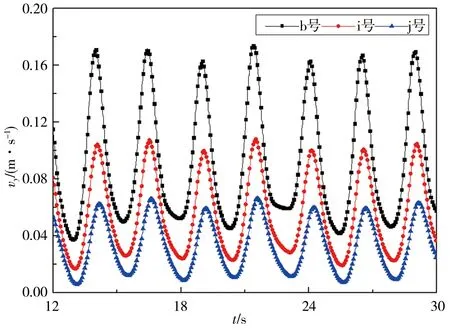
d)L/W=6

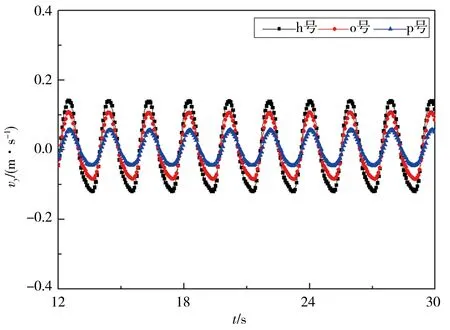
a)L/W=0

3 結論

本文建立了單矩形截面橋墩、串列雙矩形截面橋墩繞流數值計算模型，采用RNG k-?湍流模型進行非穩態瞬時求解，分析了不同橋墩間距工況下串列雙矩形橋墩繞流流場特性，獲得了渦量分布、流線及壓力分布、橫向流速分布等與橋墩間距的關系。主要結論如下。

a)與常規圓柱橋墩繞流相比，矩形截面橋墩繞流流動更復雜，尾流渦體尺寸更大，渦體及流線彎曲區橫向分布范圍更廣，橫向流速波形圖形態復雜，且峰值更大。

b)串列雙矩形截面橋墩尾流流動較單橋墩繞流更復雜，橋墩尾流渦體橫向分布范圍擴大，且流動狀態與橋墩間距緊密相關。橋墩間距影響兩側橋墩剪切層的生成、分離和重附，當L/W≥4時上游橋墩尾流才形成渦體，否則只在下游橋墩尾流形成卡門渦街，伴隨著渦體周期性地脫落。

c)流體遇橋墩時流線發生翻轉、彎曲，橋墩兩側流速增加且流線分布加密，橋墩尾流形成多個流線彎曲的低速區；串列雙矩形橋墩流線彎曲區分布范圍更廣，當L/W≥4時兩橋墩間也形成流線彎曲區。上游橋墩前方和其他側面區域分別為壓力增高區和壓力降低區，下游橋墩尾流形成多個壓力降低區，而兩橋墩間區域壓力分布受橋墩間距影響。

d)上游橋墩前方出現呈對稱分布的正負橫向流速區，橋墩尾流橫向流速沿水流方向呈正負交替分布；串列雙矩形橋墩間距越大，橋墩間正負橫向流速區分布越多，橫向流速峰值越低。單橋墩繞流橫向流速波形圖單一且呈對稱分布，串列雙矩形橋墩時上游橋墩后方區域橫向流速波形圖不再對稱分布，局部出現二次波動，且橫向流速波動峰值較單橋墩增大，距離橋墩中心線越遠波動峰值越低。