兩種偽距IFB模型在多系統(tǒng)融合精密單點定位中的性能分析

趙 班 熊永良 秦星敏

1 西南交通大學(xué)地球科學(xué)與環(huán)境工程學(xué)院，成都市犀安路999號，611756

精密單點定位(PPP)技術(shù)[1]僅采用單臺接收機即可獲得高精度位置參數(shù)，具有精度高、不受地理位置限制等特點，還可以提供額外參數(shù)用于物理、氣象等其他方面研究[2]。目前全球衛(wèi)星系統(tǒng)主要有GPS、GLONASS、Galileo和BDS，由于測站分布和衛(wèi)星星座幾何分布存在差異，各衛(wèi)星系統(tǒng)在定位精度和收斂時間方面表現(xiàn)各不相同，為得到穩(wěn)定精確的坐標，融合多系統(tǒng)的PPP應(yīng)運而生。多數(shù)研究選擇忽略偽距IFB誤差或按照頻率號的一次線性函數(shù)估計載波IFB[3-6]。Zhou等[7]總結(jié)各衛(wèi)星系統(tǒng)的最優(yōu)偽距IFB模型，但僅對GLONASS單系統(tǒng)和GPS/GLONASS組合系統(tǒng)進行分析。同時大多數(shù)研究采用的組合觀測值會放大噪聲誤差，也無法對其他參數(shù)進行估計。

因此，本文提出多系統(tǒng)非差非組合PPP函數(shù)模型，對兩種IFB模型在不同衛(wèi)星組合模式下的定位精度和收斂速度進行統(tǒng)計分析。

1 多系統(tǒng)融合PPP的函數(shù)模型

線性化后不同衛(wèi)星系統(tǒng)的偽距和載波觀測方程可表示為：

(1)

(2)

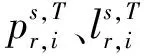
為方便理解，通常對符號進行如下定義：

(3)

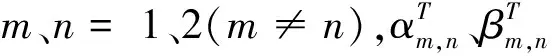
由于在PPP中已使用基于無電離層模型計算的精密衛(wèi)星鐘差產(chǎn)品，因此其提供的衛(wèi)星鐘差產(chǎn)品包含衛(wèi)星端UCDs的線性組合[8]。將式(3)代入式(1)和式(2)可得：

(4)

(5)

2 系統(tǒng)偏差I(lǐng)SB

在進行多系統(tǒng)融合PPP時，需要考慮不同衛(wèi)星系統(tǒng)間的系統(tǒng)偏差I(lǐng)SB，ISB可看作為不同衛(wèi)星系統(tǒng)接收機鐘差的差異[6]，需要選擇一個衛(wèi)星系統(tǒng)作為基準。例如以GPS為基準，則GLONASS衛(wèi)星的ISB參數(shù)為：

(6)

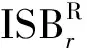
3 兩種偽距IFB模型

3.1 第一種偽距IFB模型

第一種模型是對每個GLONASS衛(wèi)星估計一個IFB參數(shù)：

(7)

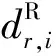
(8)

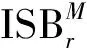
3.2 第二種偽距IFB模型

第二種模型是用頻率號的一次線性函數(shù)來估計偽距IFB參數(shù)：

(9)

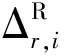
(10)

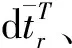
4 兩種偽距IFB模型性能分析

為研究兩種偽距IFB模型在多系統(tǒng)融合PPP中的性能，隨機選取52個MGEX測站在2020-04-09～15期間的數(shù)據(jù)(采樣間隔為30 s)進行分析。在進行數(shù)據(jù)解算時發(fā)現(xiàn)有些測站大部分歷元搜索到的GLONASS衛(wèi)星個數(shù)小于4，在數(shù)理統(tǒng)計上無意義，因此僅對G/R、R/B、R/E、G/R/B、G/R/E、R/B/E和G/R/B/E等衛(wèi)星組合模式進行性能評定。將不同組合估計的坐標與IGS周解坐標[10]進行對比，獲得E、N、U三個方向上的坐標殘差，并分析不同組合模式在靜態(tài)和動態(tài)條件下采用不同偽距IFB模型對定位精度和收斂時間的影響。

4.1 靜態(tài)定位精度分析

圖1和圖2為不同組合模式下兩種偽距IFB模型在靜態(tài)條件下的定位精度。從圖中可以看出，兩種偽距IFB模型的定位精度在3個方向上大致相當。在E方向上，R/B、R/B/E組合第二種模型的精度略優(yōu)于第一種模型，其他組合精度相當；在N方向上，R/B組合第二種模型的精度略優(yōu)于第一種模型，其他組合精度相當；在U方向上，R/B、R/E、R/B/E第二種模型的精度略優(yōu)于第一種模型，其他組合精度相當。綜上所知，在衛(wèi)星數(shù)量較少的情況下，第一種偽距IFB模型的參數(shù)個數(shù)多于第二種模型，從而使定位精度降低。

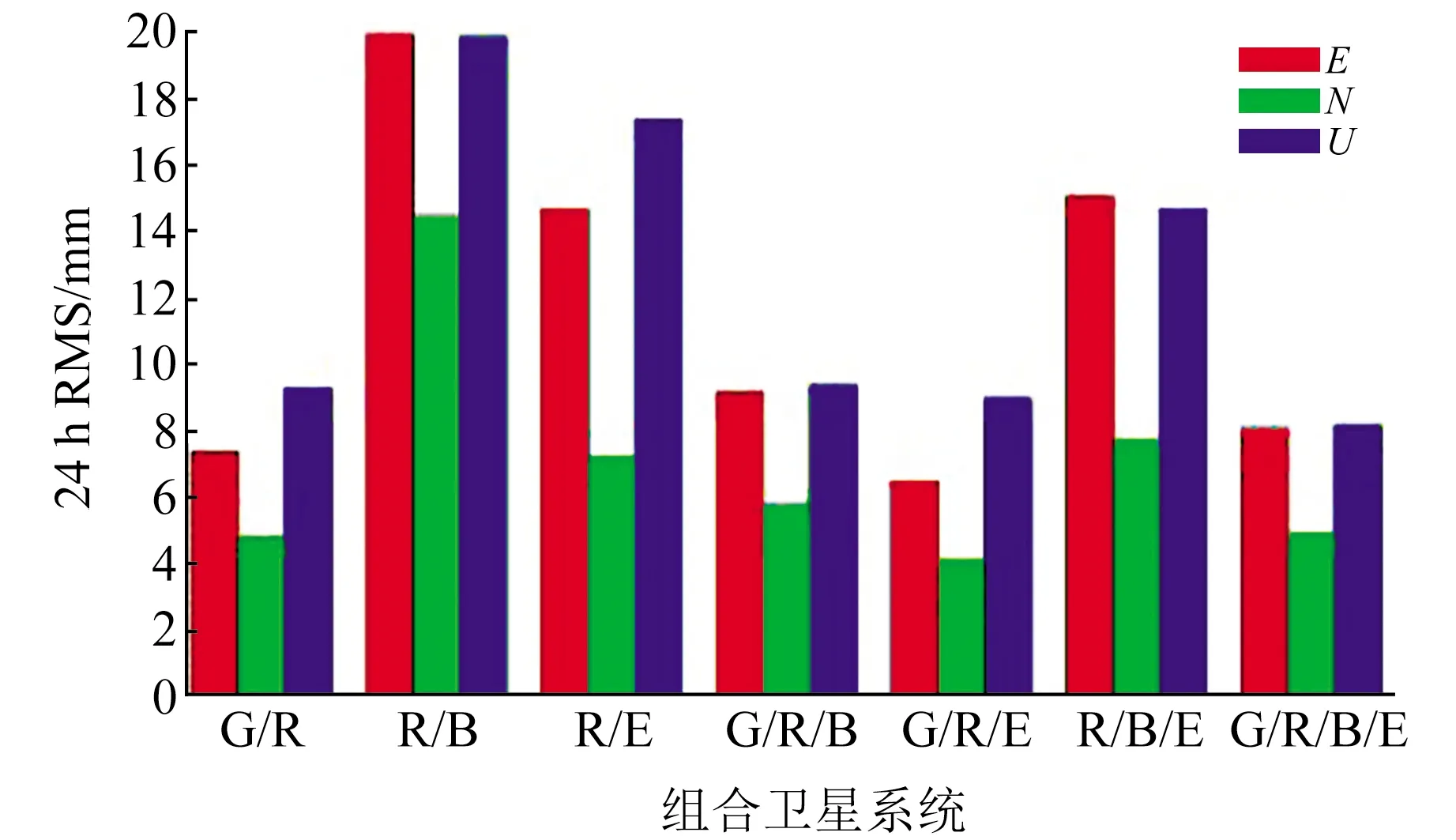
圖1 第一種IFB模型靜態(tài)定位結(jié)果

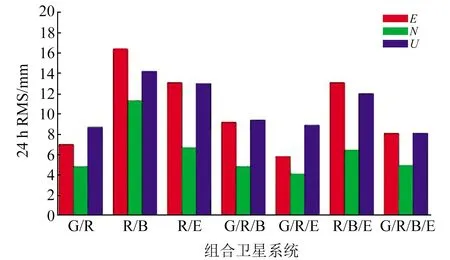
圖2 第二種IFB模型靜態(tài)定位結(jié)果

4.2 動態(tài)定位精度分析

圖3和圖4為不同組合模式下兩種偽距IFB模型在動態(tài)條件下的定位精度。通過對比可知，在N方向上，第二種IFB模型的定位精度比第一種模型提升約21%；在E方向上，R/E組合第二種模型的定位精度優(yōu)于第一種模型；在U方向上，R/E、R/B、R/B/E組合第二種模型的定位精度優(yōu)于第一種模型。其他組合在E、U方向上定位精度大致相當。

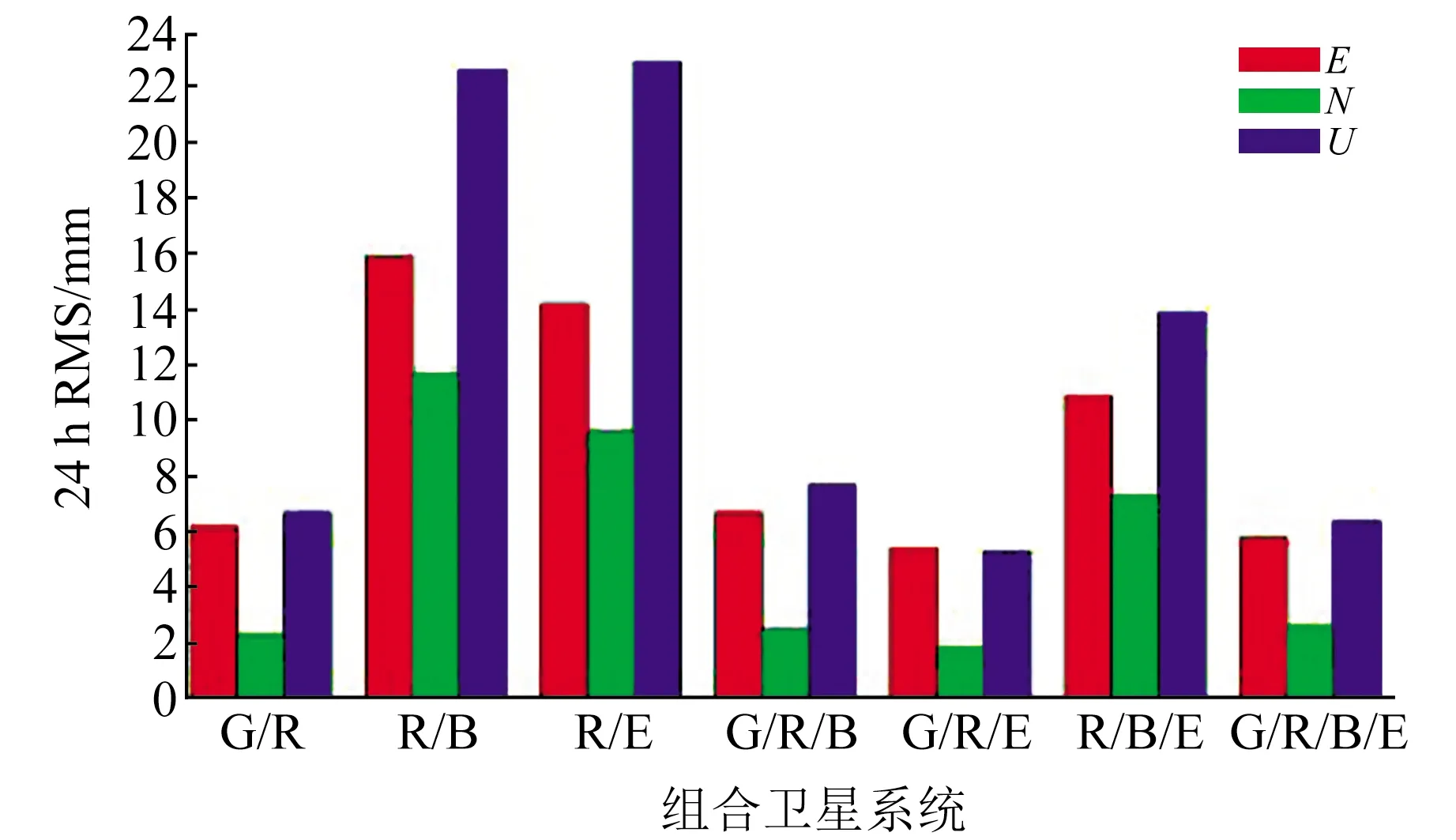
圖3 第一種IFB模型動態(tài)定位結(jié)果

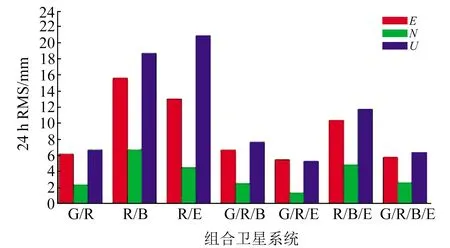
圖4 第二種IFB模型動態(tài)定位結(jié)果

4.3 收斂速度分析

為評估兩種偽距IFB模型在多系統(tǒng)融合PPP中的收斂速度，將收斂時間定義為：68%和95%的總測站在3個方向上均達到一定精度并在隨后的一段時間內(nèi)保持穩(wěn)定所需的時間。靜態(tài)條件下3個方向上精度達到0.03 m并在隨后至少20個歷元內(nèi)保持穩(wěn)定的歷元時間為收斂時間，動態(tài)條件下3個方向上精度達到0.1 m并在隨后至少20個歷元內(nèi)保持穩(wěn)定的歷元時間為收斂時間。表1～7(單位min)分別為G/R、R/B、R/E、G/R/B、G/R/E、R/B/E和G/R/B/E在靜態(tài)和動態(tài)條件下3個方向上的收斂時間。

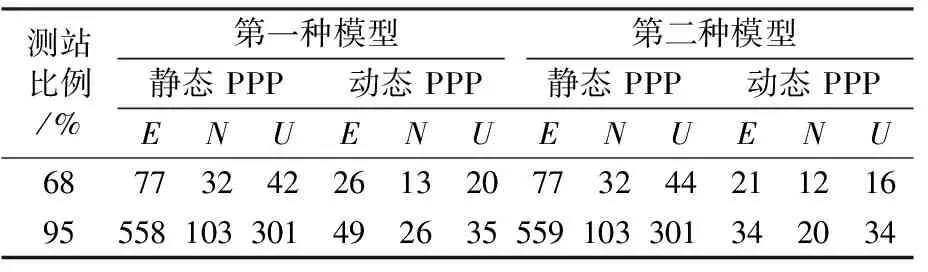
表1 G/R收斂時間

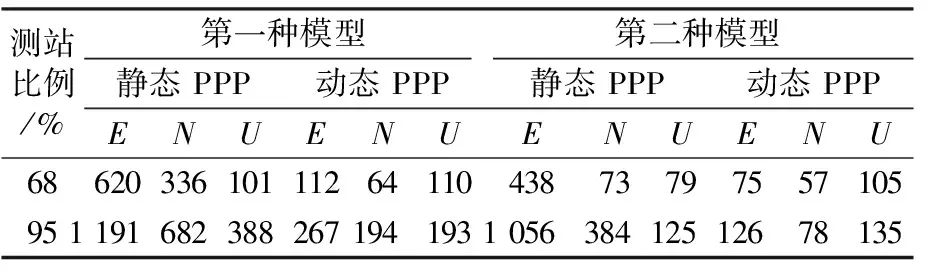
表2 R/B收斂時間

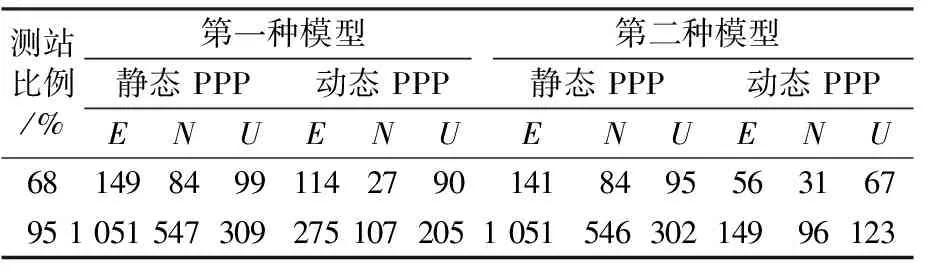
表3 R/E收斂時間

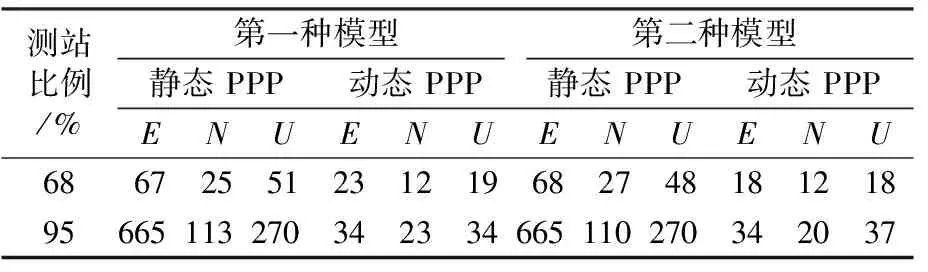
表4 G/R/B收斂時間

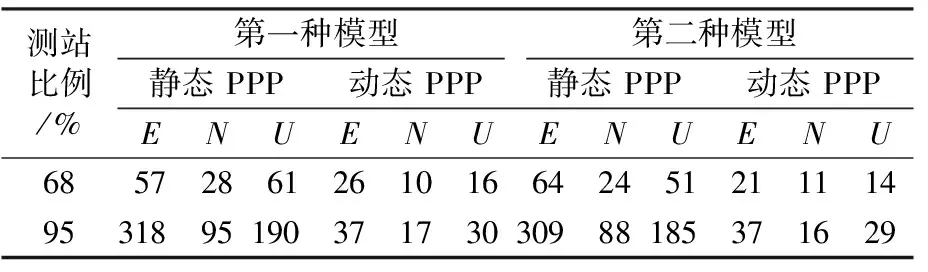
表5 G/R/E收斂時間

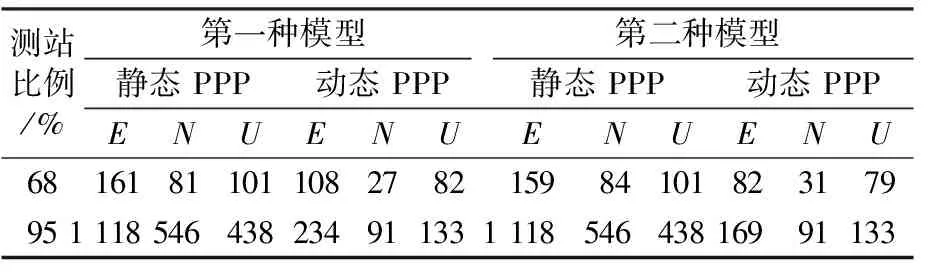
表6 R/B/E收斂時間

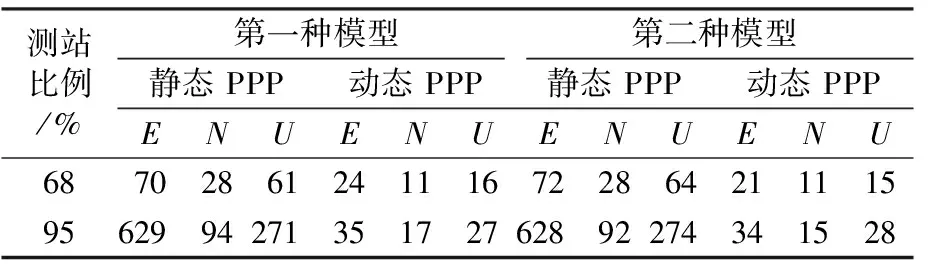
表7 G/R/B/E收斂時間

由表1～7可知，在包含GPS星座的組合中，第一種模型在部分方向的收斂速度略快于第二種模型，但提升幅度有限。原因可能為GPS衛(wèi)星在全球分布較廣，每個歷元能觀測到的GPS衛(wèi)星數(shù)目較多且隨時間變化較小。但其他不包含GPS衛(wèi)星的組合在動態(tài)條件下第一種模型的收斂速度普遍比第二種模型慢，且部分方向的收斂速度相差巨大。原因主要為第一種偽距IFB模型包含大量被估參數(shù)，并且該組合的衛(wèi)星會受到地域、時間等因素影響，每個歷元觀測到的可用衛(wèi)星數(shù)量變化很大，數(shù)值解不穩(wěn)定。

5 結(jié) 語

1)靜態(tài)條件下，兩種偽距IFB模型在3個方向上定位精度相當；動態(tài)條件下，兩種偽距IFB模型在E、U方向上精度相當，第二種IFB模型能夠提高N方向上定位精度，提升幅度約為21%。

2)兩種模型在不同衛(wèi)星組合模式下的收斂速度略有不同。包含GPS星座的組合在靜態(tài)和動態(tài)條件下第一種模型的收斂速度在部分方向上略快于第二種模型，但提升效果有限；不包含GPS星座的組合第一種模型的收斂速度在3個方向上普遍比第二種模型慢，且部分方向的收斂速度相差巨大。

3)兩種偽距IFB模型在3個方向上均可達到設(shè)定精度，但第一種模型會增加被估參數(shù)的個數(shù)，這在數(shù)值運算中會影響解算精度，特別是在觀測方程較少的情況下。因此從模型簡易程度、定位精度和收斂時間等方面考慮，第二種偽距IFB模型要優(yōu)于第一種偽距IFB模型。