基于客戶新裝、增容戶數關聯分析下的區域用電量增長預測
李常生,許星煜,石 磊,李 揚,靳文麗
(國網甘肅省電力有限公司酒泉供電公司,甘肅 酒泉 735000)
經濟的快速發展,電力需求的不斷提高,現有容量已經不能滿足實際情況。隨著客戶申請新裝、增容的數量不斷增加,客戶新裝、增容也成為電力負荷預測不可忽略的一部分。負荷預測的準確性將直接影響到電力企業投資、電力系統網絡布局及運行的合理性。另外,根據準確的電力負荷預測結果可以經濟合理地安排電網內部發電機組的啟停,保持電網運行的安全穩定性,減少不必要的旋轉儲備容量,合理安排機組檢修計劃,保障社會的正常生產和生活,有效地降低發電成本,提高經濟效益和社會效益。所以,基于客戶新裝、增容戶數關聯分析對電力負荷預測的研究急需開展。
1 區域用電量增長預測方法
本文提出的基于客戶新裝、增容戶數關聯性分析下的區域用電量增長預測方法流程如圖1所示。

圖1 基于客戶新裝、增容戶數關聯性分析下的區域用電量增長預測方法流程
首先計算第t年和第t-1年對應月份的電量差值ΔQ和對應月份用戶新裝增容戶數差值Δn之間的皮爾遜相關系數ρxy(Pearson Correlation Coefficient)和斯皮爾曼相關系數rs(Spearman's Rank Correlation Coefficient)。
根據ρxy、rs判斷ΔQ與Δn是否存在相關關系。若兩變量之間不存在相關關系,則區域用電量預測不必考慮用戶新裝、增容戶數的影響;若存在相關關系,則根據ρxy、rs的相對大小判斷兩變量之間是否存在線性關系。
當ρxy≈rs時,即|ρxy-rs|<ε,ε是一個很小的正數,變量之間存在線性關系,利用線性回歸擬合ΔQ與Δn之間的線性表達式ΔQ=WΔn+b。當ΔQ與Δn之間不存在線性關系時,利用多項式擬合ΔQ與Δn之間的表達式ΔQ=,m是多項式階數。
2 相關性分析
相關性分析用來分析變量之間的相關關系。常用來描述變量之間的相關關系的指標是皮爾遜相關系數和斯皮爾曼相關系數。
皮爾遜相關系數ρxy用來度量兩個變量之間的線性關系。斯皮爾曼相關系數rs反映變量之間的變化趨勢的方向和程度。與皮爾遜相關系數相比,斯皮爾曼相關系數評估變量之間的單調關系,不易受到錯誤值和極端值的影響。
3 回歸分析
3.1 線性回歸
線性回歸分析常用于研究自變量與因變量之間的線性相關性[1]。線性回歸擬合參數簡單,計算量小,計算速度快,但只能擬合線性關系。
線性回歸分析的模型:

式中,βi,i=0,1,2,…,n是回歸系數,且與xi,i=0,1,2,…,n無關。
若存在n個獨立觀測數據[bi,ai1,ai2,…,aim],其中,bi為y的觀察值,aij是xij的觀察值,i=1,2,…,n,j=1,2,…,m(n>m)。
由式(1)可得:
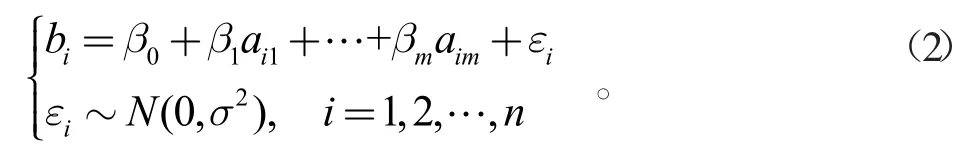
利用最小二乘估計,使得誤差平方和最小,即可得到回歸系數β,如式(3):

3.2 多項式回歸
多項式回歸可以擬合變量之間復雜的非線性關系,但多項式回歸計算量大,并且多項式階數不易確定,計算速度慢[2]。
多項式回歸分析的模型:

式中,βi,i=0,1,2,…,m是回歸系數,m是多項式階數。
假設目前存在n組數據樣本(x1,y1)、(x2,y2)、…、(xn,yn)。其中,yi為第i個樣本的輸出真實值,y^i為根據式(4)擬合的輸出值(i=1,2,…,n),最小化損失函數,如式(5),即可得到最優擬合參數β。

3.3 評估指標
3.3.1 均方誤差
均方誤差(Mean Squared Error,MSE)反映了預測數據與原始數據之間的差異。
3.3.2 擬合優度
擬合優度是指回歸曲線對觀測值的擬合程度,反映了回歸曲線對觀測值信息的利用程度。度量擬合優度的統計量是可決系數R2。R2越接近1,說明回歸曲線的觀測值擬合程度越好。假設目前存在n組數據樣本(x1,y1)、(x2,y2)、…、(xn,yn)。其中,yi為第i個樣本的輸出真實值,y^i為擬合值(i=1,2,…,n)。定義兩個指標:總平方和SST和回歸平方和SSR,如式(6)。

可決系數R2的公式:

4 算例分析
本文選取3個典型地區電量數據,時間范圍為2017年1月到2019年12月,共36個數據點,包括月份用電量和當月用戶新裝、增容戶數。
電量差值ΔQ與用戶新裝、增容戶數差值△n的相關系數見表1。

表1 ΔQ與Δn的相關系數
由表1可以看出,地區1的ΔQ與Δn沒有相關關系,所以在用電量預測時,可以不用考慮用戶新裝、增容戶數對用電量的影響。地區2的ρxy和rs都比較大,且兩者的值接近,所以地區2的ΔQ與Δn有強線性關系,可以用線性回歸擬合。地區3的ΔQ與Δn具有相關關系,但ρxy明顯小于rs,所以兩者可以用多項式擬合。
調用matlab2018a工具箱cftool對地區2進行線性回歸擬合,如圖2所示。

圖2 地區2ΔQ與Δn的線性回歸圖
圖2中,在置信度為95%的情況下,擬合直線為ΔQ=0.000395Δn+0.000716。擬合結果的MSE=1.741×10-6,R2=0.902,可以準確地根據地區2的Δn預測出ΔQ。
調用matlab2018a工具箱cftool對地區3進行多項式回歸擬合,如圖3所示。
圖3中,擬合曲線的最高項為3次項,系數擬合在置信度為95%的情況下,擬合曲線表達式如式(8):

圖3 地區3ΔQ與Δn的多項式回歸圖

擬合結果的MSE=0.001,R2=0.996,可以準確地根據地區3的Δn預測出ΔQ。
5 結論
基于受到客戶新裝增容的影響,電量的變化是單調變化這一假設,本文提出基于客戶新裝、增容戶數關聯性分析下的區域用電量增長預測方法。利用皮爾遜相關系數和斯皮爾曼相關系數,確定ΔQ與Δn之間的相關關系,并針對不同情況選擇不同方式擬合兩者的表達式:若ΔQ與Δn線性相關,則使用線性擬合,避免復雜的多項式計算;若ΔQ與Δn非線性相關,則使用多項式擬合,確保得到Δn與Δn之間精確的表達式。最后通過算例分析證明了該方法的有效性。

