基于有限狀態機的UUV 集群圍捕策略研究

李亞哲姚 堯馮景祥尤 岳

(江蘇自動化研究所,江蘇 連云港 222006)

0 引言

無人水下航行器(UUV)自20世紀60年代發展至今,已廣泛應用于各大領域,包括近海石油勘探、水下安保、水下通信線路的鋪設與維修等民用領域以及水下搜索、偵察、獵雷、反潛作戰等軍用領域。然而隨著海洋資源進一步的開發以及水下作業力度的加大,單個UUV 在獲取信息、任務處理以及控制執行力等方面有明顯的局限性,難以獨自完成復雜的工作任務。因此UUV 技術必然會朝著魯棒性更強、容錯性更好的UUV 集群的方向發展。UUV 集群技術在水下偵察、搜救、圍捕等任務中也得到了廣泛應用。其中UUV 集群圍捕任務經常被用來檢測和評價UUV 集群系統的性能。隨著智能無人集群體系理論的發展,其仿真及驗證也得到了極大的提高。近年來,該問題成為UUV 集群領域的一個熱點課題。

文獻[6]根據人類的認知活動提出了一種基于群體意志統一的無人機圍捕策略,有效解決了不同數量的無人機集群圍捕問題,但該方法局限于固定環境下的圍捕。文獻[7]在每個機器人都能獲取全局態勢的前提下利用循環追蹤策略解決了圍捕問題。文獻[8]通過預測虛擬目標提出一種使用相位差的神經振蕩器的基于極限環的算法,成功完成了多機器人圍捕目標的任務,但未考慮被圍捕目標的逃跑策略。文獻[9]使用強化學習的方法來訓練機器人集群模型對目標的圍捕,但強化學習有訓練時間長、學習到的新策略無法保證最優等固有缺陷。關于集群圍捕的研究,圍捕策略的設計是能否完成圍捕任務的關鍵技術之一。

現有的絕大多數研究均建立在圍捕UUV 的性能優于被圍捕UUV 性能的前提下,然而這是不現實的。因此,本文設定被圍捕UUV 的速度大于圍捕UUV,且被圍捕UUV 將采用智能的逃跑策略,這大大增加了UUV 集群圍捕的難度。本文將采用基于阿波羅尼斯(Apollonius)圓的圍捕模型,然后提出基于有限狀態機的圍捕策略,通過仿真驗證,成功實現了對目標UUV 的圍捕。

1 問題描述

本文研究的圍捕問題建立在無限且無障礙物的二維平面上,由(≥3)個圍捕UUV 對1個目標UUV 進行圍捕,最終形成以目標UUV 為中心的一個包圍圈,如圖1所示。

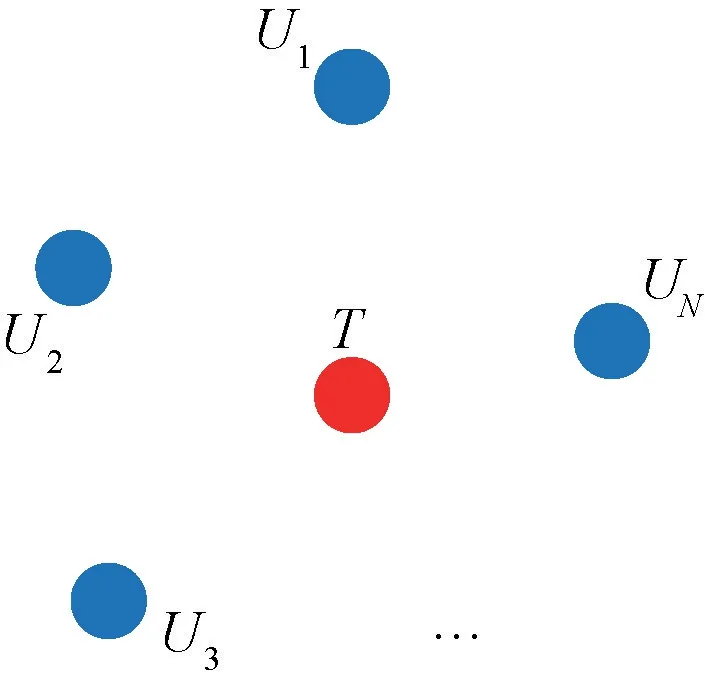
圖1 UUV 集群圍捕目標

圖1中,{,,…,U },表示個圍捕UUV 的集合,表示被圍捕的目標UUV,用V 表示圍捕UUV 的速度,V 表示目標UUV 的速度。為提高所設計的圍捕策略的普適性,本文允許V ＞V 。

圍捕任務開始后,圍捕UUV 按照UUV 集群尾部策略進行圍捕,同時目標UUV 按照設定的逃逸策略進行逃逸。當圍捕UUV 包圍目標UUV 并在其周圍形成封閉的Apollonius圓時,視為圍捕成功。

2 模型構建

2.1 UUV 運動學模型

本文采用國際水池會議(ITTC)及造船工程學會(SNAME)推薦的坐標系和參數符號描述UUV的運動。對UUV 的建模過程參考文獻[10]。

根據研究的需要,不考慮UUV 在垂直方向上的運動,即假設UUV 只在水平面內運動。這里定義[,,],為運載體坐標系在地面坐標系下的廣義位置坐標,如圖2 所示。定義[,,],為UUV 的廣義速度。其中,和分別表示UUV 在運載體坐標系下沿水平面的2個坐標軸方向的速度,為艏向角速度。

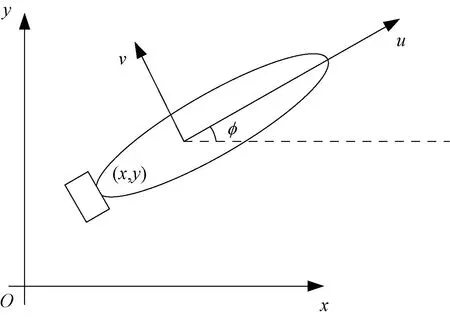
圖2 UUV 水平面運動圖示

則UUV 的運動學模型為:

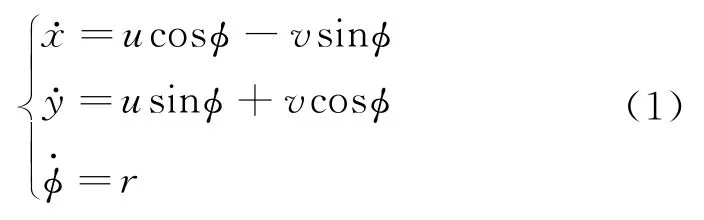
2.2 UUV 集群圍捕模型

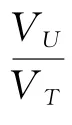
根據圍捕UUV 與目標UUV 會同時到達Apollonius圓上一點這一特性,設計UUV 集群圍捕模型如圖3所示。

圖3 為個 圍 捕UUV 即,,,…,U 與目標之間構建基于Apollonius圓的UUV 集群圍捕模型。其中,點,,,…,O 為Apollonius圓的圓心。當某2個相鄰的Apollonius圓沒有相切或相交時,目標UUV 可利用速度優勢,憑借智能逃逸策略突破包圍圈,進行逃逸;當所有相鄰的2個Apollonius圓相切或相交時,個圍捕UUV形成封閉Apollonius圓域,圍捕成功。

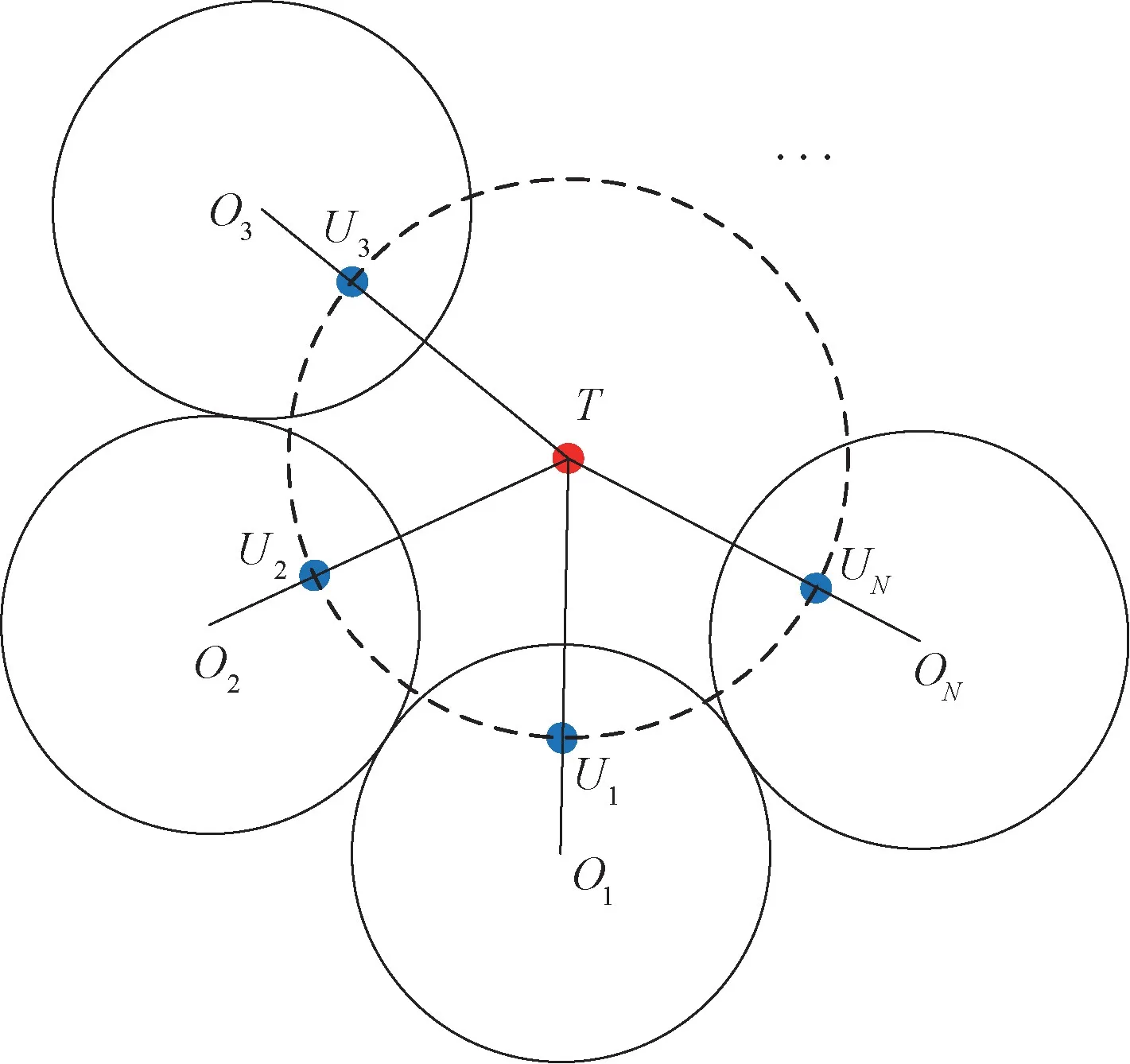
圖3 UUV 集群圍捕模型

2.3 目標UUV 逃逸策略

目前圍捕問題中被圍捕者的傳統逃逸策略為將所有追捕者的速度方向進行矢量疊加,并朝著疊加后的總速度方向以最大速度進行逃逸,然而傳統的逃逸策略不夠智能化。本文將以UUV 集群是否對目標UUV 形成包圍圈作為研究,提出一種智能的逃逸策略,討論如下:

(1) 如圖4所示,目標UUV 計算以目標為頂點、相鄰UUV 與自身所形成的角度,當有角度大于或等于180°時,即≥180°,判定為UUV 集群未對目標UUV 形成包圍圈,這時目標UUV 采用傳統的逃逸策略,以最大速度朝的方向逃逸。

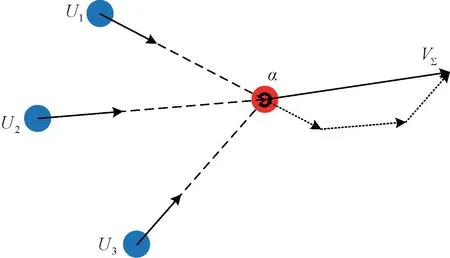
圖4 目標UUV 未被包圍逃逸方向示意圖

(2) 當目標UUV 計算相鄰UUV 與自身所形成的夾角,所有夾角均小于180°時,如圖5 所示,＜＜＜180°,判定為UUV 集群未對目標UUV 形成包圍圈。此時目標UUV 采取“最大夾角”逃逸策略,即選擇形成最大夾角的2個圍捕UUV(和)連線的中點方向V 作為逃逸方向。

圖5 目標UUV 被包圍逃逸方向示意圖

3 基于有限狀態機的UUV 集群圍捕策略

3.1 有限狀態機基本理論

有限狀態機是系統根據用戶定義的規則在有限的狀態之間進行轉換,最終處于結束狀態或消亡狀態的一種數學模型。

由于目標UUV 的性能高于圍捕UUV,UUV集群無法追捕目標。因此本章主要分析在UUV 集群圍捕過程中設置合理的誘捕策略進行圍捕,即在實時策略選擇過程中對UUV 集群狀態進行轉換的策略。建立有限狀態機模型,對UUV 集群狀態轉換規則進行詳細研究,最終實現了UUV 集群圍捕的有效決策。

3.2 基于有限狀態機的UUV 集群圍捕策略設計

3.2.1 UUV 集群圍捕策略狀態設計

UUV 集群圍捕就是對目標形成包圍圈并縮小的過程。假設所有的UUV 均勻速運動,且V ＞V ,UUV 集群無法通過簡單的追捕捕獲目標,本章設計了合適的伏擊圍捕策略,每個決策階段都由多個基本狀態構成,包括潛伏狀態、追捕狀態、攔截狀態和合圍狀態。

(1) 潛伏狀態

圍捕UUV 進入潛伏狀態時,停止運動且僅打開被動聲納,噪音極小,無法被目標UUV 發現,即圍捕UUV 處于潛伏狀態時不會對目標UUV 的運動產生任何影響。

(2) 追捕狀態

當處于追捕狀態時,圍捕UUV 以最快的速度朝向目標運動。

(3) 攔截狀態

攔截狀態是指相鄰2個圍捕UUV 相互靠近、缺口變小的運動狀態。

(4) 合圍狀態

合圍狀態是指UUV 集群成功包圍目標,且形成封閉Apollonius 圓域,即UUV 集群成功圍捕目標。

3.2.2 UUV 集群圍捕策略設計

當UUV 集群在無速度優勢的條件下對目標UUV 實施圍捕時,可以通過潛伏、誘導等策略對其進行圍捕。對于單目標UUV 來說,圍捕UUV 的數量越多,圍捕越容易,成功率越高,本文取最小值=3,如圖6所示,正三角形虛線區域為伏擊圈。此時如果能找到一個合適的圍捕策略,使得3個圍捕UUV 包圍目標并形成封閉Apollonius圓域,就能圍捕成功。

對于圍捕UUV 的策略選擇,輸出的控制量為啟動信號和轉角方向,對應的是圍捕UUV 的狀態轉換,各狀態記為(,,,),其中s (0,1,2,3)分別表示UUV 的潛伏狀態、追捕狀態、攔截狀態和合圍狀態。定義(,,,)為輸入集,其中用于判斷目標是否進入伏擊圈,即用1表示目標進入伏擊圈,0表示目標未進入伏擊圈。取或或,表示圍捕UUV 與U (1,2,3)之間的距離大小,設為預設閾值,將d (1,2,3)的具體值分別在3個區間內進行匹配,分別為(0,),(,2),(2,∞),對應模糊歸一化集合[小(),中(),大()]。在,,中取值,描述的是目標UUV 的運動方向。如圖6所示,通過判斷目標UUV 的運動方向與圍捕UUV 和目標連線所成的夾角θ(1,2,3)可以決策進入攔截狀態的圍捕UUV。將θ(1,2,3)的當前值與3 個論域的值匹配,分別為(0°,30°),(30°,90°),(90°,180°),對應 模 糊 歸一化集合[小(),中(),大()]。1表示所有圍捕UUV全部脫離潛伏狀態,反之至少有1個圍捕UUV 處于潛伏狀態。接下來對UUV 集群圍捕策略進行設計。

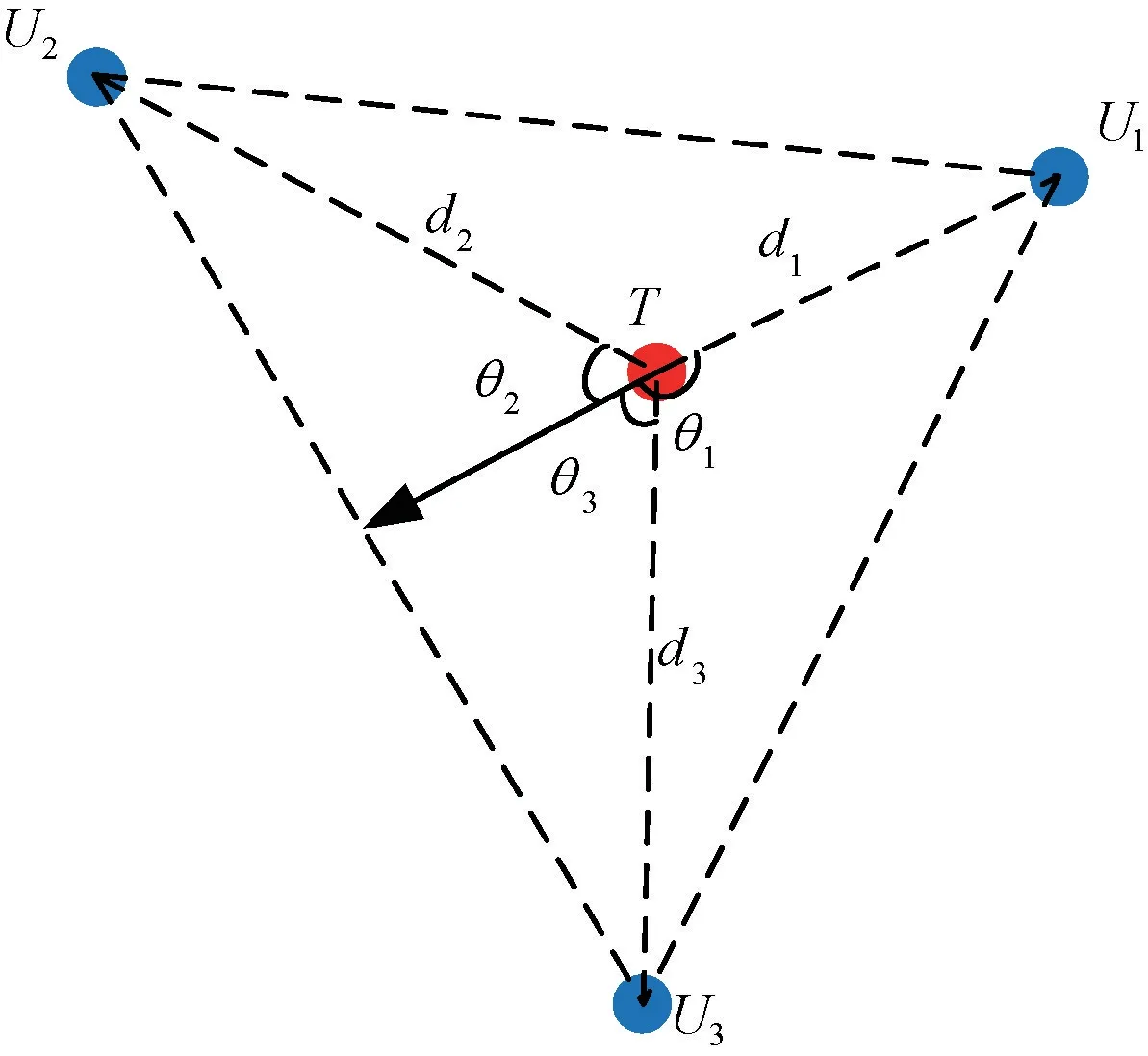
圖6 輸入集示意圖

由于V ＞V ,所以在目標UUV 進入伏擊圈之前,各圍捕UUV 保持潛伏狀態。目標進入伏擊圈后,與目標之間的距離小于設定啟動閾值的圍捕UUV 進入追捕狀態。根據目標UUV 的智能逃逸策略,當3個圍捕UUV 全部進入追捕狀態時,目標UUV 將采取“最大夾角”逃逸策略,因此目標運動方向上相鄰的2個圍捕UUV 將進入攔截狀態。在此期間,為縮小包圍圈,當目標UUV 運動方向與自身和某圍捕者U 連線所成夾角小于某閾值時,U 將處于追捕狀態。在追捕狀態和攔截狀態下,UUV集群包圍圈將逐漸縮小,最終成功圍捕目標UUV。UUV 集群圍捕示意圖如圖7所示。

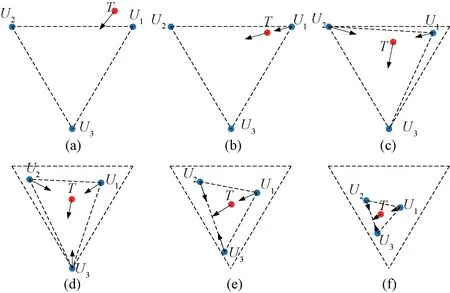
圖7 UUV 集群圍捕示意圖

基于上文設計的圍捕策略,本文首先設定UUV 集群圍捕目標UUV 的任務為。反映了圍捕UUV 狀態轉換和選擇的規則,用簡化的四元組表示為(,,,)(由于最終狀態只有一個,所以這里忽略了最終狀態的集合),其中表示從一個狀態變換到另一狀態的轉換規則,→。

狀態轉移規則如下:

if0 andandand0 then圍捕者選擇狀態;

if1 andandand0 then圍捕者選擇狀態;

……

因為圍捕者、、完全等價,所以各圍捕者具有相同的狀態轉移規則,以為例,其全部狀態轉移規則如表1所示。

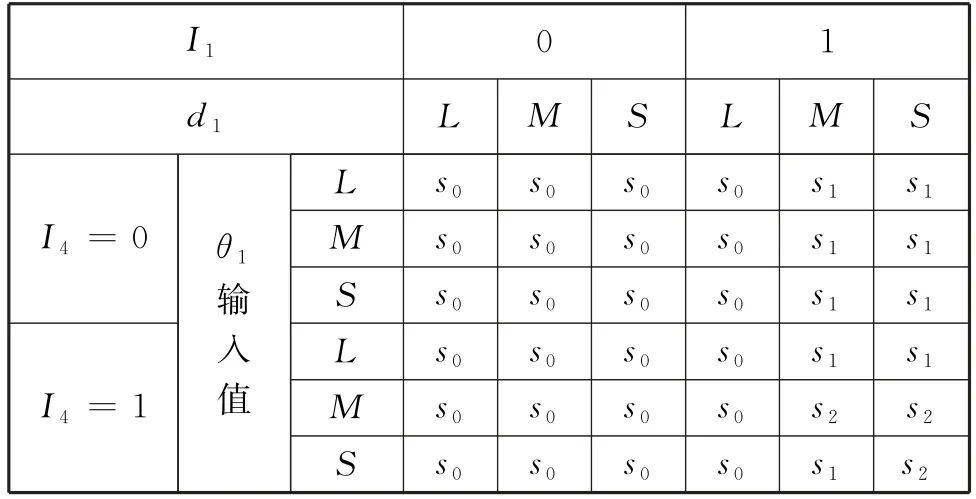
表1 圍捕者UUV狀態轉移規則

4 仿真研究

本實驗使用的是Matlab仿真環境。假定目標UUV 一直處于可以被UUV 集群感知的狀態,且目標UUV 只能探測到處于運動狀態的目標,無法探測到處于潛伏狀態的圍捕者。圍捕UUV 和目標UUV 的運動均受單位時間內最大角速度的限制。UUV 集群圍捕失敗的判定條件為目標UUV 移動到包圍圈之外。實驗相關參數設置如下:

預設啟動閾值為70 m;圍捕成功閾值為25 m;目標UUV 的速度V 為1.4 m/s;圍捕UUV的速度V 為1.2 m/s;圍捕UUV 初始位置坐標為(1 000,214),(200,1 600),(1 800,1 600)。

如圖8所示,圍捕初始時刻,圍捕UUV 集群保持三角伏擊陣型并處于潛伏狀態,目標UUV 從起點(1 400,1 800)以最大速度1.4 m/s出發。UUV集群圍捕第24 s 時刻,目標UUV 進入伏擊圈,UUV滿足啟動閾值,進入追捕狀態,UUV與UUV未滿足啟動閾值條件,仍處于潛伏狀態,目標UUV 判定自身未被包圍,采取傳統的逃逸策略。在處于UUV集群圍捕第58 s時刻,UUV與UUV先后滿足啟動閾值條件,進入追捕狀態。第58 s后目標UUV 判定自身處于圍捕包圍圈,采用“最大夾角”逃逸策略。此后,為縮小包圍圈,圍捕UUV 依據目標逃逸方向在追捕狀態和攔截狀態中切換,目標被圍捕UUV 形成相鄰的Apollonius圓無縫隙地包圍。最終UUV 集群將目標UUV 限制在了一個較小區域,且各圍捕UUV 均滿足圍捕成功閾值條件,判定為圍捕成功。整個圍捕過程持續154 s。

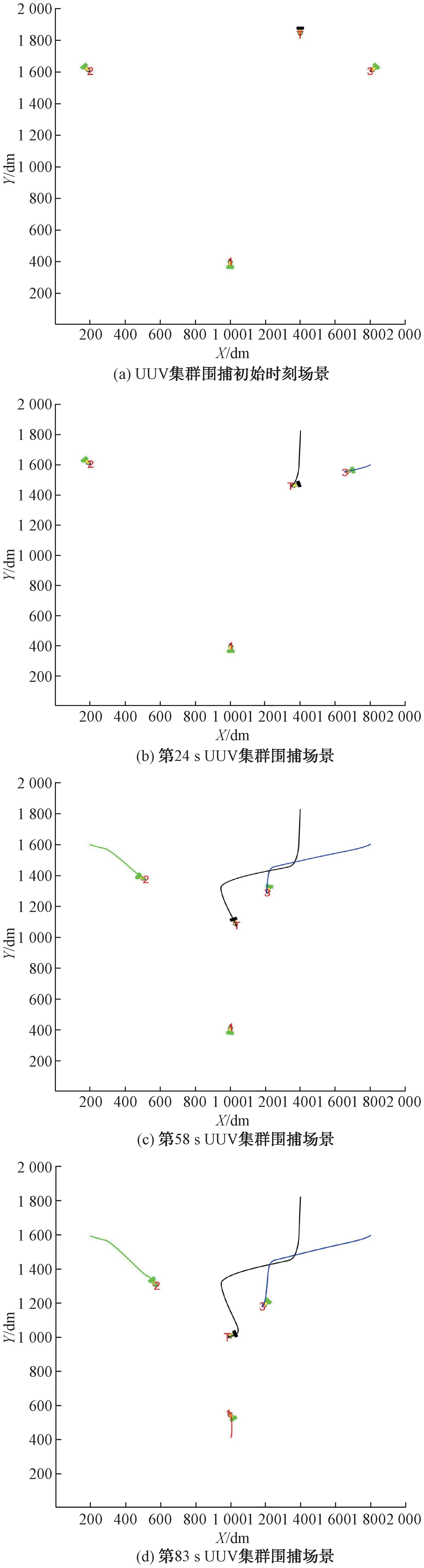
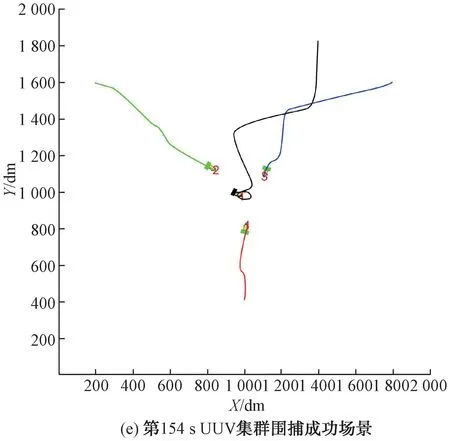
圖8 UUV 集群圍捕仿真圖

5 結束語

本文在被圍捕目標速度性能高于圍捕者的前提下,提出一種基于有限狀態機的UUV 集群圍捕策略。針對進入UUV 集群圍捕伏擊圈內部目標的圍捕,設計了4種圍捕者狀態,并對狀態轉換規則進行了詳細設計。最后,在Matlab仿真環境下驗證了所提出圍捕策略的有效性。