基于改進弦高誤差約束的機器人曲面磨削軌跡規劃

詹慶榮， 段鵬飛， 吳路路， 江本赤

(安徽工程大學 機械工程學院，安徽 蕪湖 241000)

0 引言

打磨機器人是機器人工業化的一個典型代表，主要被用來對一些形狀較為復雜的零件進行打磨拋光[1]，能有效解決手工磨削存在的費時、費力、生產效率低下、加工質量不穩定等問題[2-3].在機器人自動打磨系統中，穩定的磨削力、高精度的打磨軌跡是影響磨削質量的兩個重要因素，其中磨削軌跡是打磨的基礎[4-5].

為了提高機器人磨削的精度，國內外學者作了大量研究.趙艷梅[6]提出一種基于IGS文件滿足弦高誤差的NURBS曲面軌跡規劃方法，可以生成弦高誤差約束下的自由曲面的加工軌跡.然而，在通過弦高誤差進行曲面軌跡規劃時，會遇到在曲率較大處弦高誤差超過約束的問題.Lv等[7]提出一種自由曲面的曲率變化特性自適應的軌跡規劃方法，通過優化提取刀觸點，使規劃得到的軌跡弦高誤差在約束范圍內.但該方法需要計算大量的提取點，過程繁瑣復雜.Sun等[8]提出一種基于Hilbert曲線的路徑生成算法，通過調節生成路徑的覆蓋密度，保證了拋光精度.Han等[9]基于掃描模式的物理均勻覆蓋路徑規劃方法，提出一種有效的迭代逼近算法.但文獻[8-9]規劃的路徑過于復雜，使用機器人拋光時，需要頻繁變換姿態，拋光效率較低.王浩等[10-11]以葉輪作為切削對象，對3次B樣條插補算法進行了改進，得到的切削路徑實現了平穩、高精度運行，但他們忽略了刀具與葉輪的接觸狀態.甘亞輝等[12-13]提出采用自適應變阻抗的力跟蹤控制策略，實現對環境變化的力控制，但由于建模困難,控制方法難以應用于實際加工.文科等[14-16]通過對機器人的誤差標定，使機器人定位精度得到提升，提高了機器人打磨精度，但他們沒有考慮機器人的末端姿態對機器人定位精度的影響，在磨削軌跡方面也有欠缺.

針對機器人磨削自由曲面的軌跡規劃精度問題，本文提出一種基于改進弦高誤差約束的磨削軌跡規劃方法.在分析刀具與工件有效接觸區域的基礎上，建立磨削行距計算模型；改進弦高誤差法，考慮曲面曲率對走刀步長的影響，獲得優化的磨削軌跡，以提升磨削后工件表面的輪廓質量.

1 磨削軌跡的輪廓誤差約束算法

以直線插補形式的磨削作業影響表面輪廓質量，而以改進的等弦高誤差法進行軌跡規劃，可通過控制走刀步長確保相鄰兩個刀觸點間的弦高誤差在許可范圍內.

1.1 接觸區域確定

以平底刀具為例，為避免刀具中心的零轉速磨削，使刀軸矢量m相對于被加工曲面局部的法矢量n偏轉一個角度α，提高在進給方向V上刀觸點處的拋磨速度.如圖1所示，當刀具偏轉一個角度α后，刀具與工件的有效接觸面積隨之改變，刀具底面在垂直于進給方向V的法平面上的投影呈橢圓形，其長半軸為刀具半徑r，短半軸為e=rsinα，故接觸區域可用如下橢圓方程表示：

圖1 刀具姿態示意圖Fig.1 Schematic diagram of tool posture

(1)

1.2 走刀行距計算

記行距為K，殘余高度為hs，最大磨削深度為hmax.由于工件表面曲率影響行距計算的結果，下面分別對平面和曲面兩種情況進行計算，計算模型見圖2，其中Mi、Mi+1表示相鄰刀觸點.

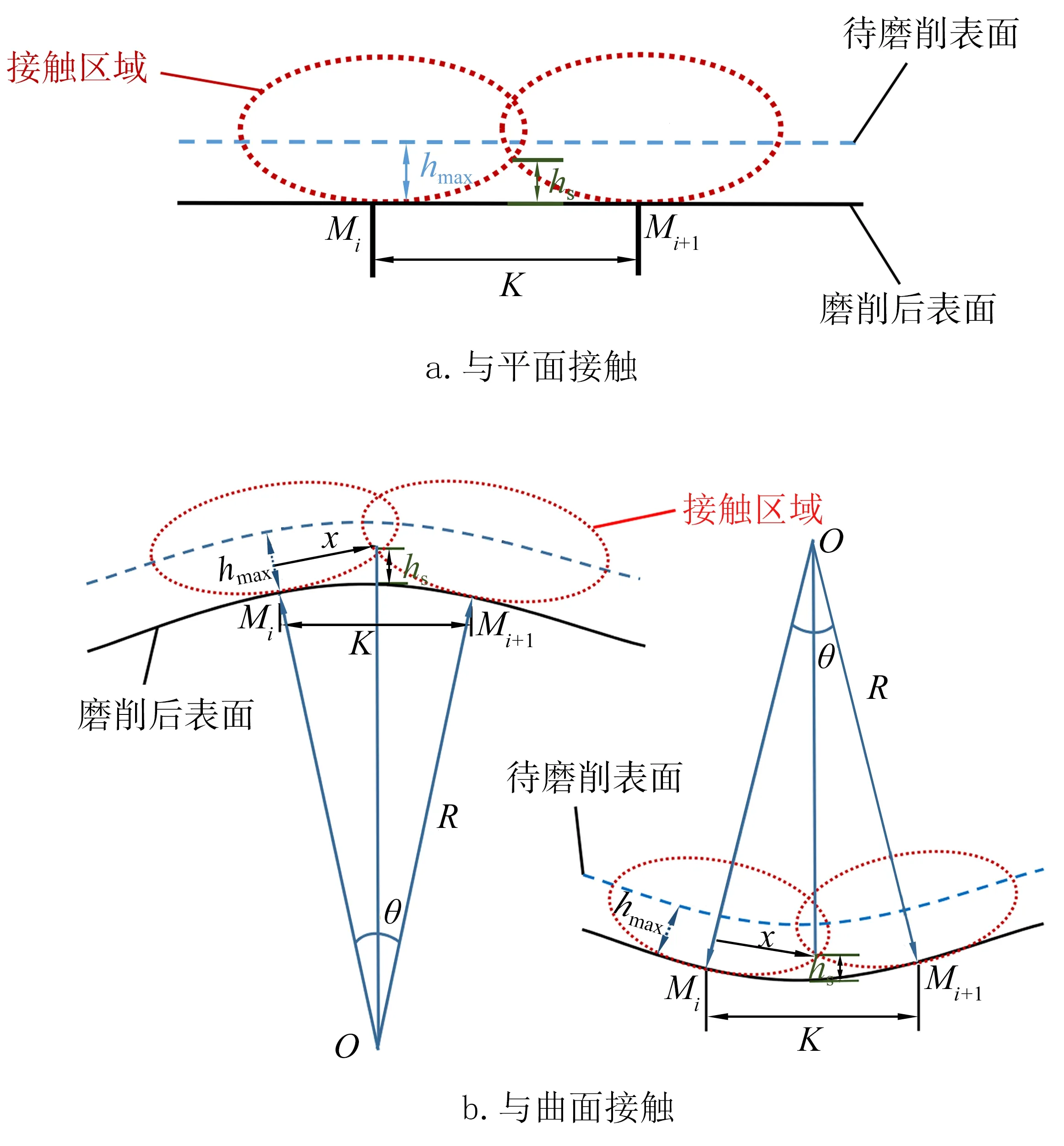
圖2 行距計算模型Fig.2 Calculation model of line space

1)刀具與平面工件接觸時的行距計算模型如圖2a所示.由式(1)知，當殘余高度控制為hs時，此時y=hs，行距K=2x，則

(2)

2)刀具與曲面工件接觸時的行距計算模型如圖2b所示，其中R為接觸區域工件的曲率半徑，θ為兩個刀觸點之間的夾角.由于相鄰刀具磨削點間隔較小，可假設曲面曲率不變.

對于凸曲面，有

(3)

(4)

對于凹曲面，有

(5)

(6)

1.3 走刀步長計算

走刀步長越大，則磨削加工誤差越大，反之亦然[17].為得到合理的走刀步長，建立如圖3所示的步長計算模型，其中R為沿走刀方向的工件表面的局部曲率半徑，H為相鄰刀觸點之間的走刀步長，ε為弦高誤差.

圖3 走刀步長計算模型Fig.3 Calculation model of cutting step length

根據幾何平面關系，對于凸曲面，有

(7)

對于凹曲面，有

(8)

1.4 改進的弦高誤差約束算法

等弦高誤差算法[18]的前提是相鄰磨削點之間的曲率基本相同，即用當前接觸點處的曲率半徑代替相鄰磨削點之間曲線的曲率半徑，根據該曲率半徑計算加工步長.從式(7)和(8)中可以看出，在給定弦高誤差時，走刀步長與當前磨削點的曲率半徑正相關.如果當前磨削點的曲率半徑Ri大大超過相鄰點之間曲線的最小曲率半徑Rmin(圖4)，則由當前磨削點曲率半徑計算的步長Hi可能過長，從而導致實際加工的弦高誤差εm過大.

圖4 實際弦高誤差超過給定誤差Fig.4 Actual chord height error over the given error

針對此問題，本文通過增加大曲率區域內磨削點的密度，對傳統的等弦高誤差算法進行改進，以提高誤差控制的曲率自適應性.具體步驟如下：

1)采用恒定弦高誤差法，計算出一系列接觸點及對應步長；

2)判斷當前弦高誤差是否超過給定誤差ε；

3)若未超過給定誤差ε，則更新起點并計算下一個磨削點；

4)若超過給定誤差ε，則比較兩個磨削點位處的曲率，以較小曲率重新計算磨削點；

5)返回第2)步，直至磨削點位全部計算完成.

1.5 優化磨削軌跡的獲取

當刀具磨削參數確定之后，磨削曲面的輪廓精度主要由行距和進給步長決定，本文通過優化磨削軌跡達到提升輪廓精度的目的.在行距方向上，根據1.2中行距與殘余高度的關系模型，通過等殘余高度約束計算出合理的行距；在步長方向上，利用改進的弦高誤差方法獲得優化的進給步長，在兩個方向上都考慮了曲面曲率的影響，示意圖如圖5所示.優化軌跡主要通過3步獲取.

圖5 優化軌跡獲取示意圖Fig.5 Schematic diagram of optimized trajectory acquisition

1)初始軌跡的選擇與離散:選取待加工曲面上邊長較長的一個邊，根據給定的弦高誤差ε，使用優化后的進給步長對初始軌跡線進行離散，得到的離散點即為刀觸點；

2)偏置軌跡:用計算得到的加工行距對初始軌跡上每一刀觸點進行偏置，連接所有偏置刀觸點，得到偏置軌跡；

3)將得到的偏置軌跡作為初始軌跡，重復上面的步驟.

2 磨削曲面表達及曲率計算

計算磨削軌跡的前提是曲面輪廓的數學表達，本文采用多數CAD系統采用的NURBS(非均勻B樣條曲面)方法進行曲面的有關計算.

設P(u,v)是一張k×l次的NURBS曲面，曲面的有理分式[19]可以表示為

其中：u,v為曲面上的參數變量；i,j為網格數量;p,q為權因子數量;Pi,j是曲面上的控制點;ωi,j是與控制點關聯的權因子;Ni,p(u)、Nj,q(v)分別定義為節點矢量U、V上的非有理B樣條基函數.

設建立的參數形式的一般自由曲面為

P(u,v)=(x(u,v),y(u,v),z(u,v)),u,v∈[0,1],

其中分量x,y,z是參數u和v的可微函數.

由于曲面上任一點有無數條曲率各不相同的曲線，為統一表示，引入法曲率.設kn為曲面一點處的法曲率，k為經過該點的曲線曲率在曲面法向上的投影，則

其中:β表示點P(ui,vi)處的單位法矢量和過該點曲線單位主法矢量的夾角;φ1,φ2表示曲面的第一和第二基本形式，則該點的曲率半徑為1/kn.

3 仿真實驗

3.1 計算軌跡數據

以埃夫特智能裝備股份有限公司開發的ER_factory軟件為平臺，基于本文算法構建磨削軌跡生成系統.該系統主要分為兩部分：1)磨削刀觸點的提取，該部分用于生成磨削軌跡與刀觸點.2)機器人運動學，該部分將獲得的刀觸點數據經六軸串聯機器人逆運動學變換轉化為關節數據，以文本方式輸出，以便后續驗證.

圖6a是選擇待加工件、設置刀具尺寸界面；圖6b是軌跡規劃相關參數的設置界面.選擇平頭磨削刀具的直徑為50 mm，殘余高度為0.05 mm，給定弦高誤差為0.1 mm，刀具軸線與刀觸點處法矢量夾角為30°，生成的磨削軌跡如圖7所示,規劃得到的刀觸點部分數據如圖8所示.

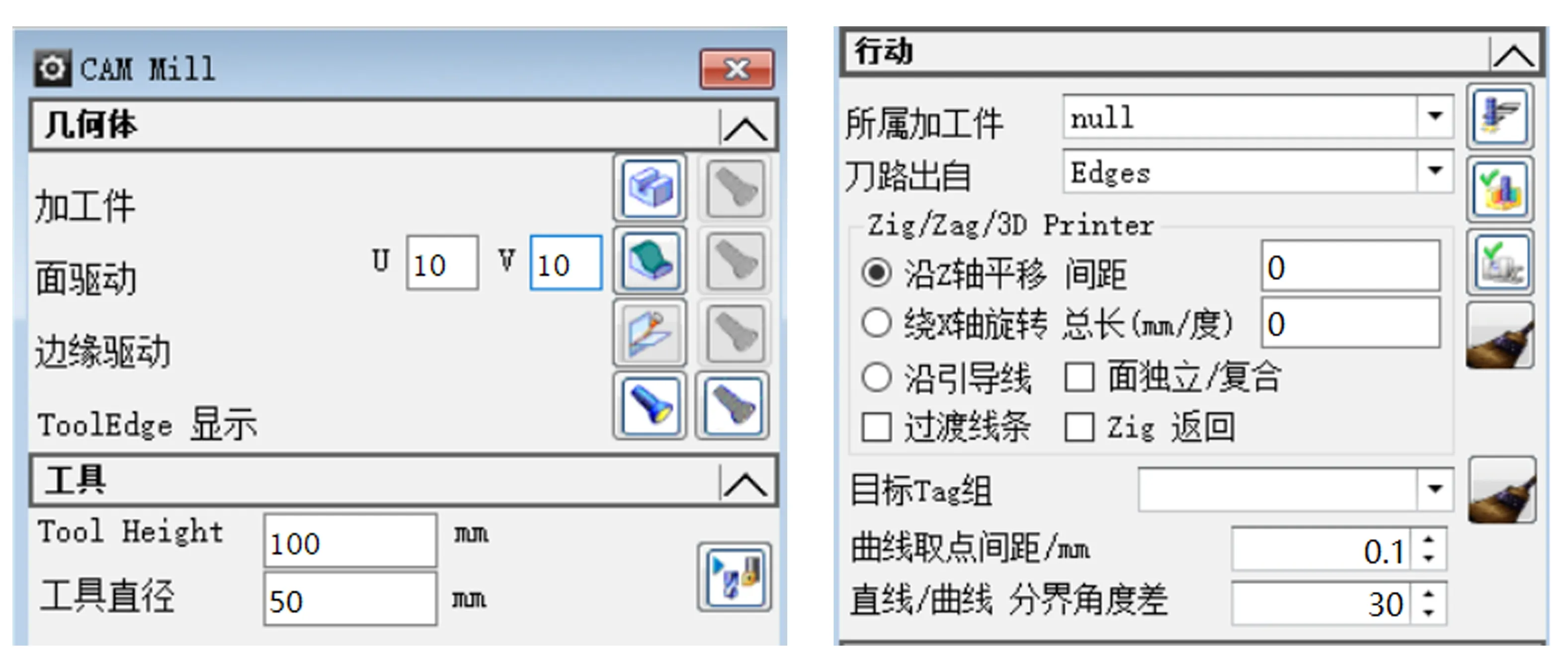
a.加工件選擇與刀具設置 b.軌跡參數設置圖6 軌跡生成平臺Fig.6 Trajectory generation platform

圖7 磨削軌跡Fig.7 Grinding track

圖8 刀觸點部分數據Fig.8 Partial data of tool location

為了驗證生成軌跡的合理性，將生成的刀觸點數據通過機器人逆運動學轉化為關節數據.仿真實驗采用的機器人為埃夫特的六軸機器人ER3B，其最大負載能力為3 kg，工作范圍為0.6 m，重復定位精度為0.02 mm，機器人相關參數見表1.

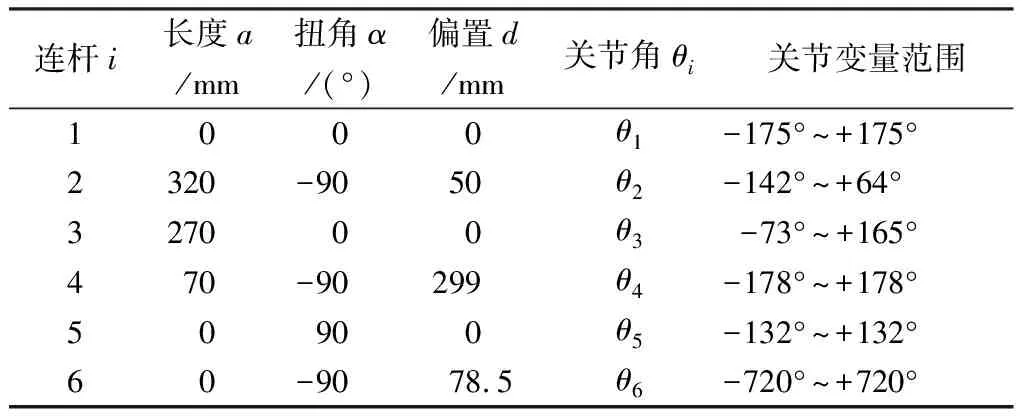
表1 ER3B機器人相關參數Tab.1 Related parameters of ER3B robot

機器人同一個末端位姿有多組關節角解，其中有些解滿足不了機器人連續運動條件.因此，在滿足連續運動條件下，以轉過的關節角度最小為標準，求出最優解[20]，得到關節角部分數據(圖9).

圖9 關節角部分數據Fig.9 Partial data of joint angle

3.2 數據分析

取圖7中的一條軌跡，分析算法改進前后的變化情況(圖10).可以看出，改進后的算法在軌跡的曲率較大處提取的刀觸點更密集，說明本文算法得到的優化軌跡能夠更好地反映曲面曲率變化情況，曲率自適應性更好.

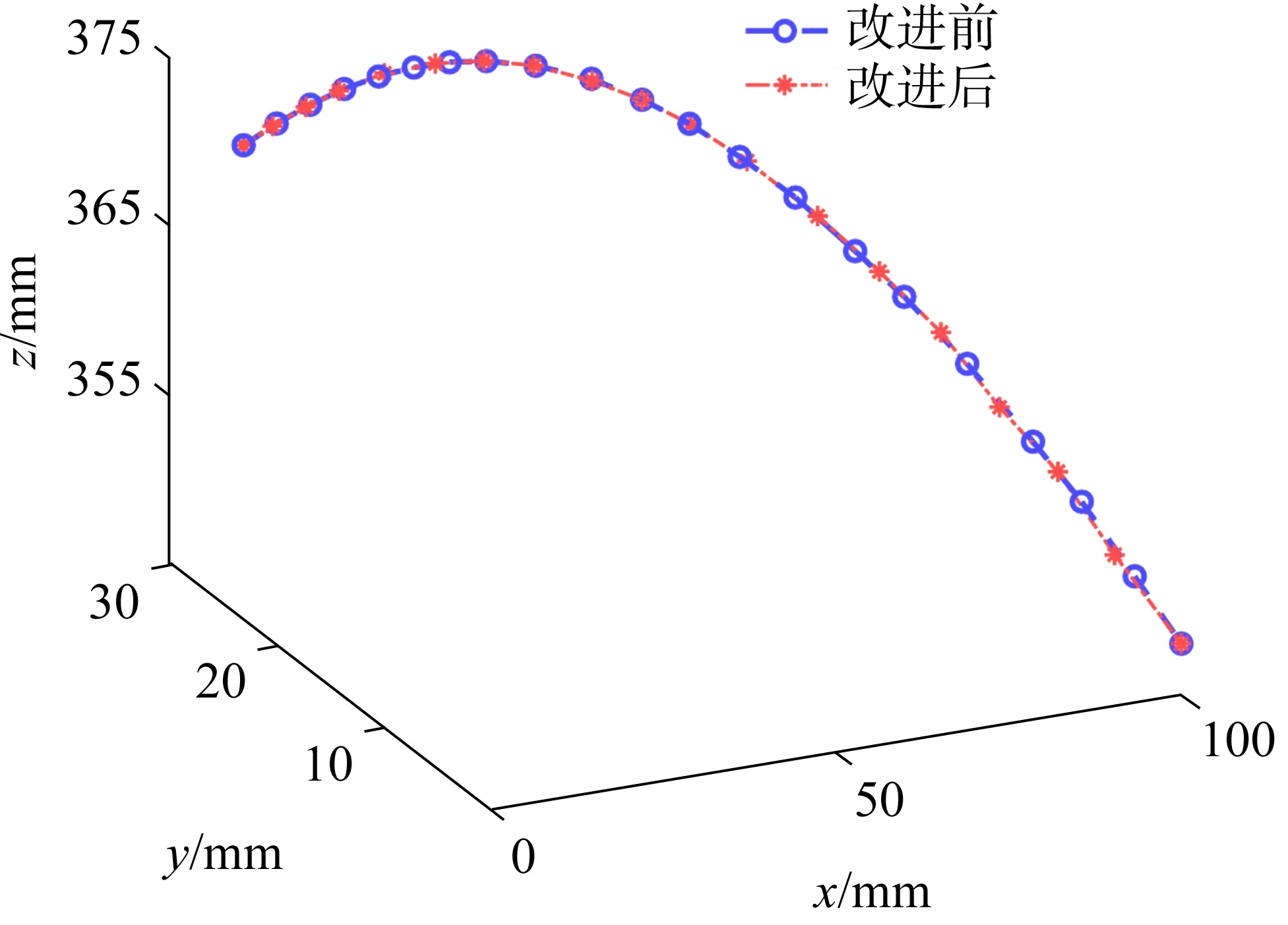
圖10 磨削軌跡刀觸點對比Fig.10 Comparison of grinding path tool contacts

進一步對比改進前后同一條軌跡上的弦高誤差(圖11).可以看出，改進前曲率較大處的弦高誤差超過0.10 mm，超出了給定的弦高誤差值,這意味著弦高誤差超出了公差，因此很容易出現過切現象.而改進后的算法將軌跡曲率較大處的弦高誤差控制在了0.05 mm左右，在給定弦高誤差范圍內，確保了加工后的工件表面輪廓精度.

圖11 弦高誤差對比Fig.11 Comparison of chord height error

4 結論

為提高曲面磨削的輪廓精度，本文給出了一種基于改進弦高誤差約束的機器人磨削軌跡規劃方法，該方法結合計算的走刀行距與步長，獲得了優化的磨削軌跡.通過與改進前的算法對比發現，本文方法在軌跡線曲率較大處提取的刀觸點更加密集，改善了磨削軌跡在步長方向的弦高誤差，可將弦高誤差有效地控制在給定弦高誤差范圍內，這表明優化后的軌跡曲率自適應性更好，能提高磨削后的曲面輪廓質量.