談數列復習需要關注的四個問題

張 輝特級教師 趙 濤

(北京市陳經綸中學)

數列的特點在于數字排列的有序性和規律性,數列問題的研究是要找出數列背后本質關系.數列是特殊的函數,除了有自身的研究方法,從函數角度研究數列是高考重點考查的內容之一,內容多并且與其他知識關聯性強.本文主要談數列復習中四個值得關注的問題.

1 尋找項an 與項數n 的關系是探求數列特點的關鍵

1.1 歸納是尋找項an 與項數n 關系的根本方法

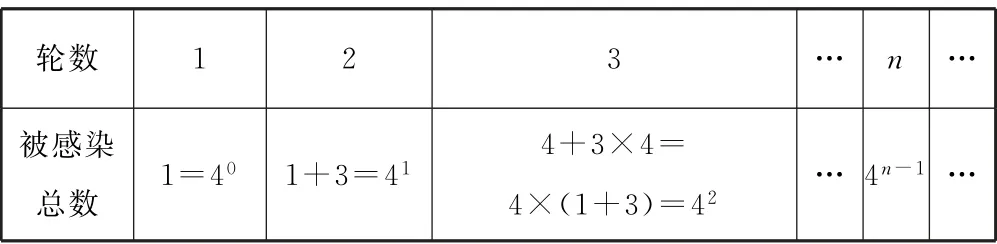
表1

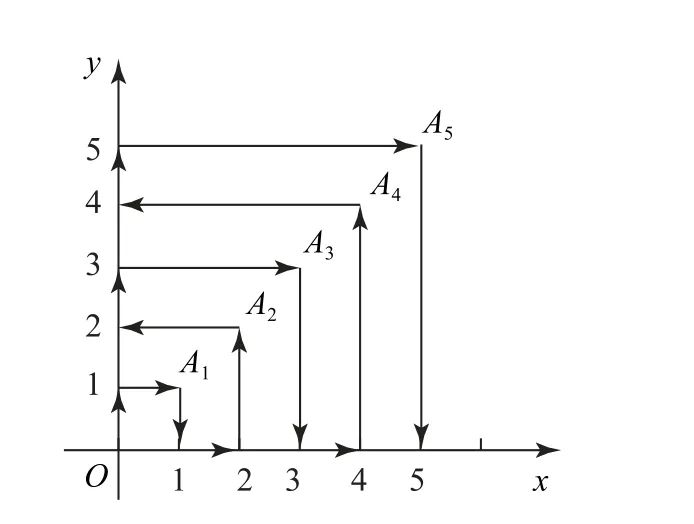
圖1

表2

因為an＝n(n＋1),且44×45＝1980,所以運動了1980秒時到點A44(44,44),又由運動規律知,A1,A2,…,An中,奇數點處向下運動,偶數點處向左運動,到達A44(44,44)時,再向左運動42秒到達點(2,44),即運動2022秒這個粒子所處位置為(2,44).

上面兩個例子都是通過歸納找出一般性規律,再去解決特殊問題,歸納是發現數列一般規律的重要方法.例2中,觀察前后項關系由a1＝2,a2＝6,a3＝12,a4＝20,….a2－a1＝2×2,a3－a2＝2×3,a4－a3＝2×4,…,an－an－1＝2n(n≥2,n∈N*),將以上各式相加有an－a1＝2×(2＋3＋4＋…＋n),所以an＝n(n＋1).

1.2 遞推是尋找項an 與項數n 關系的常用方法

解決數列問題時,有時也可以找到前后項的關系,利用它們的關系求出數列的特殊項,有時甚至能求出數列的通項公式.例2點評中就是利用遞推關系求數列通項公式的累加法.這種方法源于課本等差數列通項公式的推導,課本中推導等比數列通項公式所采用的方法是累乘法.

例3 正整數按如圖2所示的形式排列,位于對角線位置的正整數1,3,7,13,…構成數列{an},則a7＝_________,通項公式an＝_________.

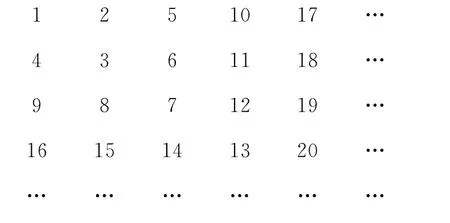
圖2

2 運用函數思想分析項an(前n 項和Sn)與項數n 的關系是解決數列問題的有效路徑

數列是一種特殊的函數,等差(比)數列的通項公式以及前n項和公式都可以看作是特殊的函數,所以借助數列的復習可以再一次學習和體會函數思想在解題中的作用.

例5 數列{an}的通項公式為an＝n2＋kn＋2,且滿足a1＜a2＜a3＜…＜an＜an＋1＜…,求實數k的取值范圍.

當4n－34＝0時,n＝8.5,即當n≤8時,an＜0;n＞8時,an＞0,所以Sn的最小值為S8,即當n＝8時Sn取得最小值.

3 明確Sn 與an 的關系,重視求和時的分類與整合思想

數列{an}的前n項和為Sn＝a1＋a2＋a3＋…＋an,其中S1＝a1,S2＝a1＋a2,S3＝a1＋a2＋a3,….任給一個n,都有唯一的Sn與之對應,所以Sn是n的函數,{Sn}也是數列,其中a1＝S1,a2＝S2－S1,a3＝S3－S2,…,an＝Sn－Sn－1.所以,an＝Sn－Sn－1是在n≥2,n∈N*的條件下才能成立的.

例8 已知等差數列{an}的首項a1＝1,公差d＞0,且第2 項、第5 項、第14 項分別為等比數列{bn}的第2項、第3項、第4項.

(1)求數列{an}與{bn}的通項公式;

4 關注數列與函數、不等式等知識的交叉、滲透與整合

總之,數列在數學知識體系中發揮著橋梁的作用,一方面它連接了函數、不等式等內容,另一方面它又為學習極限等高等數學知識奠定了基礎.數列在現實生活中有著廣泛的應用,復習過程中要抓住數列的本質特征以及數列與其他知識的關聯性,淡化技巧性,將數學學科核心素養與高中數列教學進行融合,這樣才能達到良好的復習效果.

鏈接練習

1.用火柴棒按如圖3所示的方法搭三角形.

圖3

按圖示的規律搭下去,則所用火柴棒數an與所搭三角形的個數n之間的關系式可以是_________.

2.已知等差數列{an}的公差為d,前n項和為Sn,則“d＞0”是“S4＋S6＞2S5”的( ).

A.充分不必要條件 B.必要不充分條件

C.充分必要條件D.既不充分也不必要條件