基于GIS和專家知識的滇西南地區滑坡敏感性模糊邏輯推理方法

白仙富 戴雨芡 葉燎原 聶高眾 徐碩 羅偉東 于江 徐昕

摘要：為了充分識別和有效減輕滑坡災害風險，對滇西南南澗（約470 km2）和鳳慶—昌寧（約2 300 km2）兩個研究區開展了基于GIS和專家知識的滑坡敏感性模糊邏輯評價研究。通過檢查模型計算得到的歷史滑坡點敏感性值與整個研究區域的滑坡敏感性平均值是否不同來評價本方法的性能，用Z值檢查來測試差異的統計顯著性。計算結果顯示，南澗地區的Z值為4.1，相應的P值小于0.001，表明通過模型計算得到的滑坡敏感性值是該區域滑坡事件發生的良好指標;鳳慶—昌寧地區的Z值為8.93，相應的P值小于0.001。在此基礎上，采用自然斷點法對滑坡敏感性值進行分類，根據分類結果將滑坡敏感性水平劃分成5個等級：極低（0.0～0.001）、較低（0.001～0.051）、中等（0.051～0.394）、較高（0.394～0.557）和極高（0.557～1.0）。敏感性極低和較低的地區沒有發現歷史滑坡記錄;敏感性極高地區的歷史滑坡密度約是敏感性較高地區的4倍，約為敏感性中等地區的10倍。鳳慶—昌寧地區的研究結果表明，從區域專家群中提取的滑坡敏感性與環境因子關系的知識可以外延到滇西南其它地區。

關鍵詞：滑坡敏感性;專家知識;模糊邏輯;約束算術平均法;滇西南地區

中圖分類號：P315.942 文獻標識碼：A 文章編號：1000-0666（2022）01-0118-14doi：10.20015/j.cnki.ISSN1000-0666.2022.0013

0 引言

滑坡是山區最常見的地質災害之一，它不僅對自然生態系統和人類基礎設施有重大破壞，還會造成大量人員傷亡和財產損失（Chung et al，1995;Dai，Lee，2002;Lee，Choi，2004;Guzzetti et al，2005）。為了減少滑坡災害損失和減輕滑坡災害風險，很多地區都開展了大量識別滑坡易發地點的敏感性研究（Carrara，1988;Carrara et al，1991;van Westen et al，1993;Aleotti，Chowdhury，1999;Alexander，2008;Carrara，Pike，2008），并建立了許多滑坡敏感性評估模型。受印度洋板塊持續向北東方向推擠、青藏高原地塊強烈隆起的影響，云南地區地勢從西北向南東方向逐級降低，加之河流侵蝕等外營力的影響，境內許多地區山高坡陡，滑坡現象普遍。對云南地區滑坡風險的研究一直是該區域地質災害研究的一個重要內容。隨著GIS理論與技術的興起，云南滑坡風險研究在縣（區）尺度（胡金等，2007，2008;孫黎麗等，2007;杜玉龍，方維萱，2009;錢晶，王瑞斌，2009;周松林等，2010;紀甲子等，2010;呂勇等，2010;田志萌等，2011;顏春達等，2011）、州（市）尺度（劉麗，王士革，1995;丁星妤等，2011;周松林等，2010;于豐澤，武蕾，2012;尹詩琪等，2008;張超等，2016;翟倩倩等，2016）、流域尺度（唐川，2004;謝洪等，2007;李英等，2009）和省域尺度（唐川等，1994;李志斌，鄭成德，2000;陶云等，2009;萬石云等，2013）等不同地域系統尺度的滑坡特征、滑坡環境因子、滑坡敏感性評價和區劃、滑坡治理探索等方面都取得了長足發展。

現有的大多數滑坡敏感性研究在建模時，通常用統計分析方法回歸得到歷史滑坡和滑坡點位置環境因子的關系。在訓練過程中，有滑坡的樣本數據質量總體比較可靠（van Westen et al，1993;Carrara et al，1991），而那些沒有滑坡的樣本數據質量就值得商榷。但這種建模方法存在兩方面問題：一是不能很好地識別暫時穩定的滑坡危險區。研究發現滑坡災害事件總是發生在那些沒有重點監視的區域，即在早期的風險隱患底數調查中疏漏并最終影響到了減輕風險的有效實施的區域;二是大范圍的滑坡敏感性區劃容易忽略高危型區域的“安全島”和低風險區的高隱患點，對指導具體地域減輕風險的可操作性不足。為了避開或減少以往研究方法固有缺陷的影響，本文提出一種基于GIS和專家知識的滑坡敏感性模糊邏輯評估方法。

朱阿興等（2006）對三峽地區的研究表明，專家知識用于區域滑坡敏感性評價通常能取得令人滿意的效果。由于滑坡的發生因地而異，不同研究區內影響滑坡發生的因素也大相徑庭，三峽地區與滇西南地區地理環境存在極大差異，因此不適宜直接將三峽地區的模型應用到滇西南地區。另外，對三峽地區滑坡敏感性研究采用的一些方法需要改進，如僅通過一個專家提取滑坡知識、直接使用算術平均法來計算滑坡敏感性綜合值等進行滑坡敏感性水平分區。為了改進或部分改進這些研究方法存在的不足，我們建立了新的方法，它與以往評價模型主要有兩個方面的不同：一是區域滑坡敏感性知識不是僅僅來自一位專家而是來自一個專家群，二是計算評估位置的滑坡敏感性綜合值時，不是直接使用算術平均法計算各環境因子的滑坡敏感性隸屬度指數，而是采用一種約束算術平均法來進行空間位置的滑坡敏感性綜合值推斷。最后，為了檢驗本文所提出的方法在更廣范圍地區的外延適用性，用本方法在鳳慶—昌寧地區開展滑坡敏感性評價和合理性檢驗。

1 研究方法

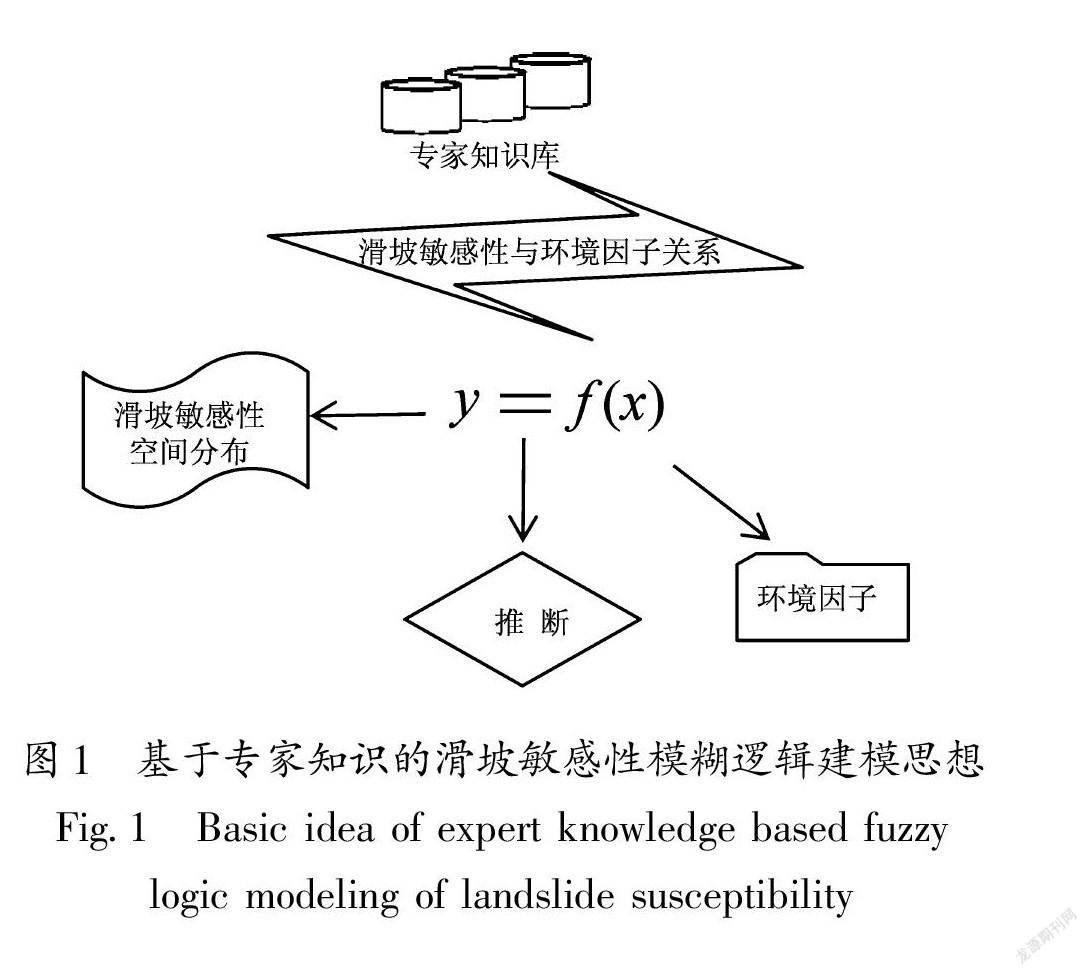
專家知識法是人們通過對物理過程的綜合理論理解和根據多年專業領域的職業經驗發展起來的一種方法（Luger，2005）。基于專家知識的滑坡敏感性建模方法的基本思想是從當地滑坡專家群里直接提取研究區滑坡敏感性與環境因子之間的關系，然后將這些關系應用于研究區各個位置的滑坡敏感性評價（圖1）。這種思路與通用的統計方法進行區域地表滑坡敏感性空間分布評價有明顯差別。專家知識法是根據區域專家群的知識對滑坡敏感性和環境因子關系f進行近似處理，而統計方法則是根據歷史滑坡事件對關系f進行統計學上的近似處理。在專家知識滑坡敏感性研究方法中，我們利用模糊邏輯提取滑坡敏感性與環境因子之間復雜的非線性關系的專家知識，并將其表示為一組模糊隸屬函數。各模糊隸屬函數用來描述滑坡敏感性與該環境因子之間的關系。在評價時，利用GIS對研究區的滑坡敏感性環境因子進行網格式地理編碼，建立滑坡環境因子柵格空間數據庫（Lan et al，2004;Fourniadis et al，2007;Remondo，Oguchi，2009），將專家知識轉化為模糊隸屬函數與GIS數據庫相結合的方式，對研究區各位置的滑坡敏感性進行推斷。

在地理建模中，專家知識模糊邏輯模型化或貝葉斯概率建模后，專家知識法的功能就比數據驅動模型所使用的統計功能更可靠、更一致、也具有更好的普適性（Fisher，1989;Hudson，1992;Zhu et al，2004）。在滑坡相關研究領域，專家通過對滑坡敏感性與環境因子之間復雜關系信息的積累形成自己的經驗性知識。基于專家知識的滑坡敏感性空間分布推斷方法包括3個主要步驟（圖2）：①從專家群里提取當地滑坡敏感性與環境因子的專家知識;②利用GIS對環境因子進行特征描述，建立區域滑坡環境因子空間柵格數據庫;③根據專家知識進行區域滑坡敏感性空間分布的模糊推斷。

1.1 專家知識提取

專家知識的質量和充分性對基于專家知識的滑坡敏感性空間分布模糊建模能否成功至關重要。本文共選取9名當地地質災害領域專家作為知識提取的對象，模型中不同環境因子的參數值采用專家給出值的調和平均數。我們從區域滑坡專家群里獲取兩類知識：①在選定的研究空間范圍內，確定影響滑坡敏感性的環境因子;②這些環境因子是如何影響滑坡敏感性的，即環境因子與滑坡敏感性之間的關系。

1.1.1 環境因子體系

專家們給出的滑坡敏感性環境因子體系對研究區的滑坡敏感性水平十分重要。區域專家的知識質量影響變量的具體內容和該變量的可外推程度。在滑坡敏感性分析中，常用的環境因子包括地形地貌（坡度、坡向、坡形、相對起伏、平面曲率和坡面曲率等地形變量）、地質構造（巖性、地層傾向和傾角等地質變量）（Oguchi，1997）、土地利用/土地覆被（土地利用類型、植被類型、植被歸一化指數等地表變量）、降水（多年平均降水量、短時最大降水量等氣象變量）等（Brabb，1984;Atkinson，Massari，1998;Aleotti，Chowdhury，1999;Dai，Lee，2002;Donati，Turrini，2002;Zhu et al，2004;Ermini et al，2005）。本文主要關注氣象條件激發的自然滑坡，人類活動、地震動參數等因子誘發的滑坡不在本文研究的考慮范疇內。

1.1.2 模糊邏輯函數建立

對于連續類型數據，在模糊邏輯領域中，函數通常表示為模糊隸屬度函數。我們用一個特定的函數來描述滑坡敏感性如何隨一個環境因子的變化而變化。模糊隸屬度函數有3種主要曲線形式：S形曲線、Z型曲線和鐘形曲線（Burrough，1989;MacMillan et al，2000;Shi，2002）。其中，常為大家熟悉的是S形曲線（圖3a），這種曲線形式用于環境因子存在有一個閾值的情況，在這個閾值上滑坡敏感性值達到最大，滑坡敏感性隨環境因子值的增大逐漸增大，當環境因子值大于該閾值時，基于環境因子的滑坡敏感性保持在最大值。Z型曲線（圖3b）是S型曲線的鏡像形式，表示本底因子在某個臨界值或某個范圍內時滑坡的敏感性最高，在臨界值時滑坡的敏感性達到最大，而大于該臨界值時滑坡的存在敏感性

會減小。鐘形曲線（圖3c）用于環境因子存在有一個最佳值或一系列最佳值的情況，在此最佳值或在此最佳值范圍內，基于環境因子的滑坡敏感性達到最大值;當環境因子值偏離該最佳值或該最佳值范圍時，基于環境因子的滑坡敏感性降低。

將滑坡敏感性和各環境因子之間的關系描述為函數f，建模時根據環境因子的有效性和重要性對f進行相應調整。根據環境因子的數據類型，f可以有不同的選擇：

fx（dij，x）=P1，x （fdij，v=c1，x）

P2，x （fdij，v=c2，x）

Pm，x （fdij，v=cm，x）（1）

式中：fx為描述滑坡敏感性與環境因子x（類別型）關系的函數，將函數計算得到的值作為滑坡敏感性值，最大為1，最小為0，敏感性值越大滑坡發生可能性越大;dij，x為位置（i，j）處環境因子x的值;P1，x，P2，x，…，Pm，x為因子x取c1，x，c2，x，…，cm，x時對應的滑坡敏感性值。在這種變量類型中，專家在提取知識時可以對每一種或一組環境因子類型對滑坡的影響進行從0到1的相對排序。

通用的高斯型函數比其它函數更容易控制曲線的形狀，使擬合的曲線盡可能逼近實際曲線的基本形狀，因此本文用高斯函數來表達函數f：

fx（dij，x）=exp-（0.8362dij，x-dxD）2（2）

式中：fx和dij，x與公式（1）定義相同;dx是影響因子x作用下隸屬函數值達到最大閾值時x的值;D是控制曲線形狀的參數，定義為隸屬度為1和0.5時環境因子值之差。曲線類型和參數根據當地專家知識來確定。若專家指出滑坡敏感性隨多年平均降水量的增加而增加，則采用S形曲線。如果專家認為，降水量大于1 500 mm（閾值 = 1 500）的地區，滑坡敏感性很高，當降水量降到1 250 mm 時（D=250），滑坡敏感性大約降低一半，就使用其它隸屬函數來計算降水環境因子作用下的滑坡敏感性隸屬度值：

fP（dij，P）=1（dij，P>1 500 mm）exp-（0.8362dij，P-1 500250）2（dij，P≤1 500 mm）（3）

式中dij，P為位置（i，j）的多年平均降水量。

1.2 研究區基礎數據處理

基礎數據處理主要是進行研究區地理編碼和環境因子柵格數據集開發。為了空間分析的方便，我們將研究區劃分為30 m×30 m的網格單元，對這些單元進行地理編碼，使得每個網格單元具有坐標位置（i，j）。在ArcGIS中將環境因子都處理為一套30 m×30 m的空間數據集，每一個像元具有對應的地理編碼。其中，大部分環境因子可以直接使用ArcGIS的功能菜單實現，比如坡度、地形起伏度、巖性（根據地質圖進行矢量處理后轉為柵格數據）、降水等，部分環境因子通過二次開發進行特征提取，比如坡形環境因子中的上凸坡、下凹坡等。

1.3 滑坡敏感性模糊邏輯推理

利用模糊邏輯推理技術，把從專家群中提取的研究區滑坡敏感性與環境因子關系同環境因子特征數據相結合，計算每個像元（根據地理編碼）位置（i，j）的滑坡敏感性模糊隸屬度來獲取整個研究區的滑坡敏感性綜合值，最后進行滑坡敏感性評價。研究區滑坡敏感性模糊邏輯推理過程如圖4所示，首先從滑坡敏感性環境因子數據集中獲取該單元的所有敏感因子值，圖中有3個環境因子，c1，x、c2，x和c3，x像元中的值分別為 1、2和3;然后，根據專家知識庫中環境因子與滑坡敏感性關系計算各環境因子值對應的滑坡敏感性模糊隸屬度。圖中，以環境因子c1，x、c2，x和c3，x為基礎的滑坡敏感性模糊隸屬度分別表示為d1ij、d2ij和d3ij。最后，基于這些單個環境因子將滑坡敏感性隸屬度值聚集起來，計算像元的總體滑坡敏感性綜合值dij。

像元滑坡敏感性值的推理過程可以用一個通用聚合函數公式來表示：

Sij=Tnx=1[fx（dij，x）]（4）

式中：Sij是像元（i，j）的滑坡敏感性;n是滑坡敏感性環境因子個數;T是計算像元（i，j）整體滑坡敏感性指數的聚合函數，對于聚合函數T可以有不同的選擇。

采用滑坡敏感性研究中常用的算術平均聚合函數（Liu et al，2004;Zhu et al，2004）計算像元敏感性綜合值，容易導致一些區域的敏感值過高。以坡形環境因子為例，平坦型坡形位置上，即使其它環境因子下的模糊函數隸屬度值很高也不會有滑坡危險，但在做簡單的聚合函數計算時可能就會得到很高的敏感性綜合值。因此我們采用約束算術平均聚合函數（式5）對評估位置滑坡敏感性綜合值進行計算。所謂約束，就是將獨立環境因子作用下滑坡隸屬度值為0的條件作為約束，將評估位置上該條件下的滑坡敏感性綜合值約束為0，以約束算術平均聚合函數推斷出整個區域的滑坡敏感性綜合值。最后再基于這個模糊的滑坡敏感綜合值，進行整個區域的滑坡的敏感性水平分級，即將滑坡敏感性水平劃分為極低、較低、中等、較高、極高5個等級。

Sij=0， fx（dij，x）=0

1n∑n1fx（dij，x），fx（dij，x）>0（5）

式中：Sij是像元（i，j）的綜合滑坡敏感性，n是滑坡敏感性環境因子個數;fx（dij，x）為位置（i，j）處環境因子x作用下的滑坡敏感性模糊邏輯模型計算值。

2 案例研究

2.1 研究區域

本文以云南省的南澗和鳳慶—昌寧地區為研究區，這2個研究區位于云南西南部，是滑坡多發區，對其進行深入研究有助于掌握風險隱患底數的國情普查和風險減輕理論的深化。南澗地區用來進行滑坡敏感性評價方法的開發和測試，鳳慶—昌寧地區位于南澗研究區以西15 km以外，用于檢驗所開發的滑坡敏感性評估方法外延的適用性。

2.1.1 南澗地區

南澗地處云南省西部橫斷山系縱谷區，位于云嶺余脈的無量山、哀牢山結合部。地勢由中南部向東北、西南逐步降低。研究區面積約為470 km2，海拔1 160～2 830 m，平均海拔2 042 m（圖5）。地形為高中山地區，除河谷流經區有少量沖積平地外，大部分為河谷、山巒和坡地構成的山區或半山區。研究區主要為南澗縣東南部的石洞寺深谷、西南部的公郎河谷及中部與西部大片山嶺地區。地貌構成主要有侵蝕構造地貌、侵蝕堆積地貌、剝蝕地貌、斷塊山地貌、巖溶地貌等。這個地區大部分的斜坡比較陡峭，最高坡度約為51°，平均坡度約為19°。區內地層主要有以下幾種類型：壩注路組、花開左組、麥初箐組、三合洞組、景星組、漾江組、外麥地巖組。

2.1.2 鳳慶—昌寧地區

鳳慶—昌寧地區是鳳慶縣和昌寧縣之間的一個矩形區域，位于南澗研究區西偏南位置，該地區長約66 km、寬約35 km（圖6）。研究區地處滇西縱谷南部，以云嶺山系和怒山山系為主，地貌依其成因，可劃分為構造侵蝕地貌、構造剝蝕地貌和侵蝕堆積地貌3大類型。區內地貌在侵蝕、構造剝蝕、沖積等地質內外應力作用下，中山、低中山、丘陵、盆地、河谷槽壩相間分布，波狀起伏，地形地貌條件復雜。這個地區大部分的斜坡比較陡峭，最高坡度約53°，平均坡度約為18°。

鳳慶—昌寧研究區地層主要有以下幾種類型：景星組、崇山巖群、壩注路組、花開左組、麥初箐組、梅家山巖群、平掌組、學習謙巖群、溫泉組、三合洞組、挖魯八組、向陽寺組、南新組、何元寨組與大寨門組并層、河灣街組、香山組、南林組、栗柴壩組、第四系全新統、漾江組、歪古村組、忙懷組、芒棒組、勐臘組、彎甸壩組、大名山組、施甸組、蒲縹組并層、魚塘寨組、南梳壩組、丁家寨組與臥牛寺組并層、丙麻組與保山一帶的沙子坡組（大凹子）未分或并層、老尖山組、仁和橋組、勐戛組、柳灣組未分、丁家寨組、丙麻組與保山一帶的沙子坡組（大凹子）未分或并層、石佛洞組、馬平組、老第三紀花崗斑巖、晚白堊世黑云母花崗巖、三疊紀花崗閃長巖、老第三紀白云母、二云母花崗巖、侏羅紀花崗閃長巖、三疊紀—二疊紀二長花崗巖。鳳慶—昌寧地區地貌和地質背景與南澗地區相似。從專家中提取的知識表明，該研究區具有與南澗地區相似的滑坡機制，這兩個研究區的滑坡敏感性與環境因子之間的關系是相似的。

2.2 南澗地區模型建立與評價

本文方法在南澗地區的建模包括3個步驟：提取專家知識、環境因子層柵格數據集地理表征和滑坡敏感性模糊推理。

2.2.1 專家知識提取

通過從當地專家群提取的滑坡敏感性與環境因子關系知識，確定了7個基本的環境因子：坡度、相對高差、坡形、地質構造、巖性、降水和土地利用類型。其中坡度的影響是最為主要的，屬于根本性環境因子，其它環境因子都是基于坡度發生作用的。地質構造對滑坡敏感性有重要影響，相似地形因子因地質構造不同而對滑坡敏感性的影響表現出較大差異。相對高差定義為斜坡山脊的最高點和山谷最低點之間的海拔差，它能夠表征整個斜坡的形狀而不是某個像元的局部曲率。

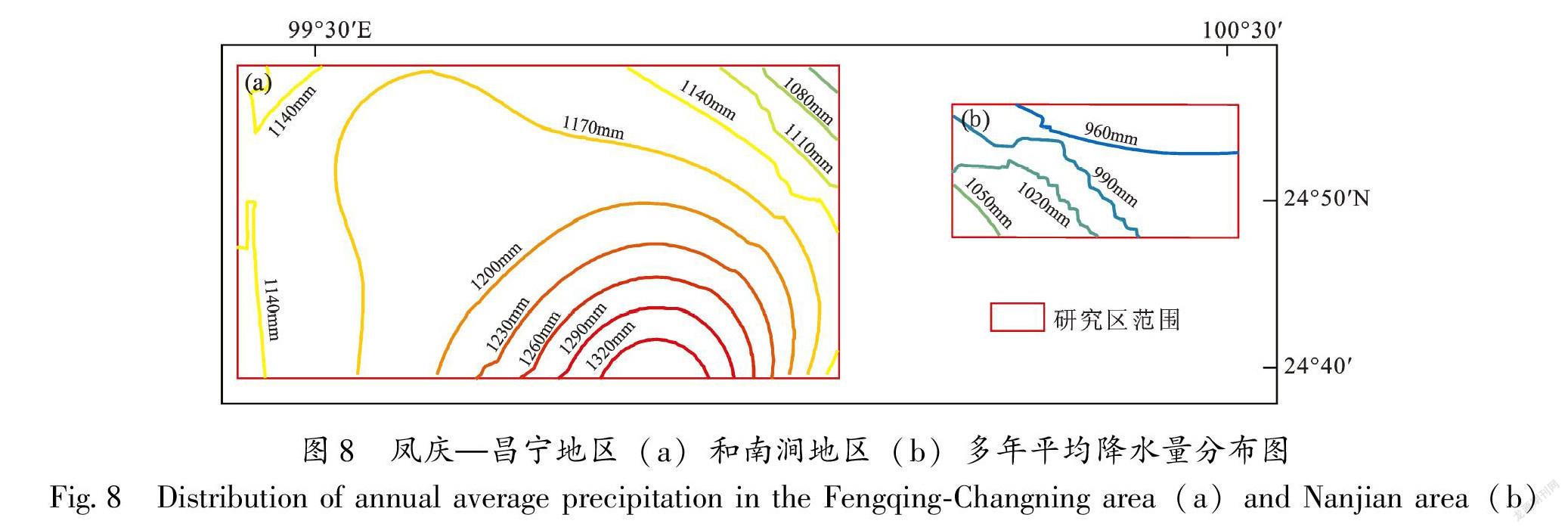
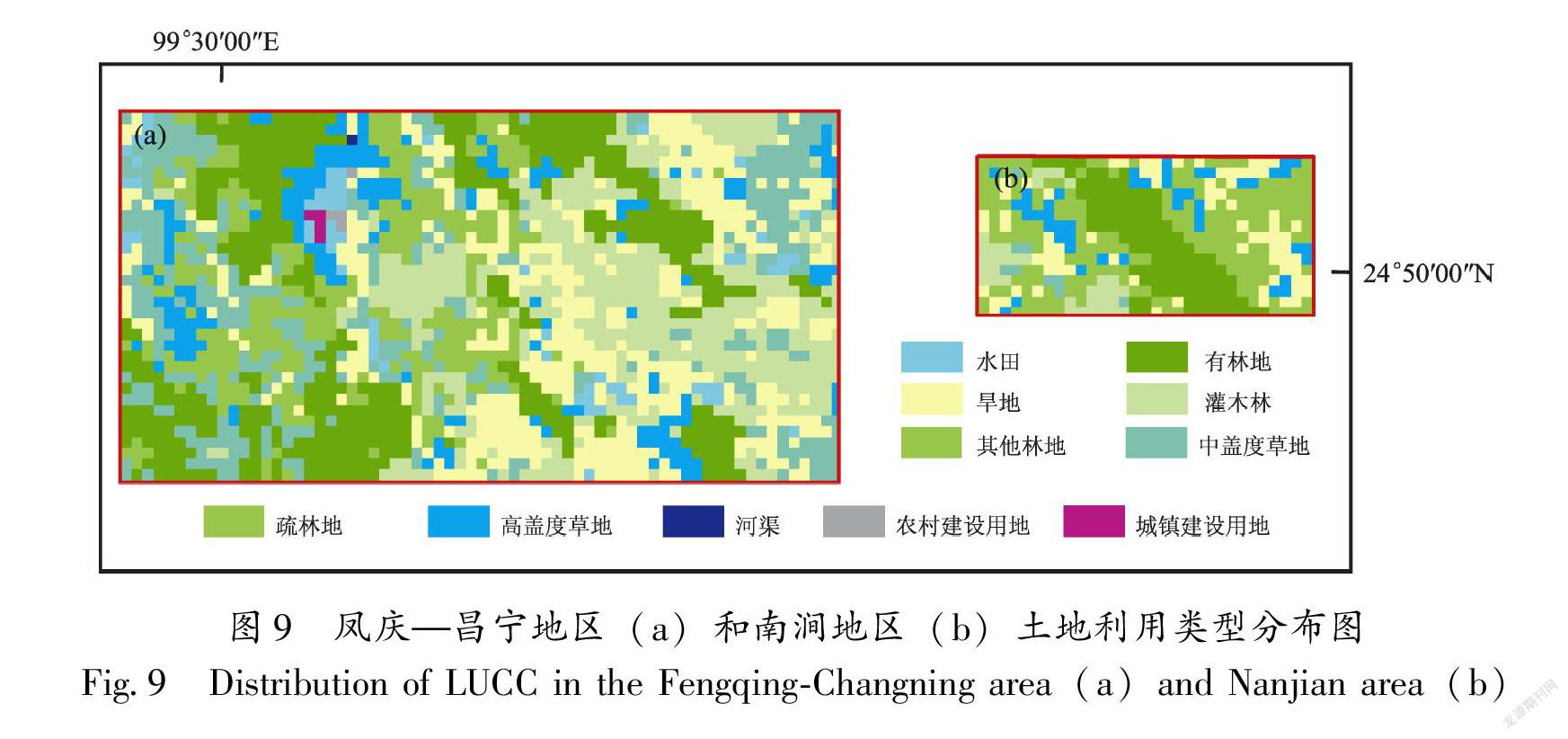
根據專家知識，將研究區斜坡形狀劃分為6種基本類型（圖7）：直型、凹型、凸型、上凸下凹型、上凹下凸型和平緩型。將研究區巖性劃分為4種基本類型：類型Ⅰ為堅硬的侵入巖巖組、堅硬的噴出巖巖組、堅硬的石英巖巖組、水體;類型Ⅱ為堅硬的片麻巖、混合巖、變粒巖巖組、堅硬的砂巖、礫巖巖組、堅硬的石灰巖、白云巖巖組、堅硬的大理巖巖組;類型Ⅲ為較堅硬的片巖巖組、較堅硬軟弱的砂礫巖夾黏土巖巖組、較堅硬、軟弱的砂礫巖、黏土巖互層巖組、較堅硬、軟弱的黏土巖夾砂礫巖巖組、堅硬-軟弱的碎屑巖夾碳酸鹽巖巖組、堅硬、較堅硬的碳酸鹽巖夾碎屑巖巖組、堅硬、較堅硬的碳酸鹽巖、碎屑巖互層巖組;類型Ⅳ為較堅硬、軟弱的千枚巖、板巖巖組、軟弱的粘土巖巖組、土體。兩個研究區為我國南方濕潤地區，境內多年平均降水量都沒有大幅度差異（圖8），土地利用類型主要有11類，根據它們對滑坡敏感性貢獻大小從小到大依次為河渠、高蓋度草地、有林地、中蓋度草地、其它林地、灌木林、疏林地、旱地、水田、城鎮用地和農村建設用地（圖9）。當地的專家根據1.1.2節所述的方法，將這些滑坡環境因子表述為模糊隸屬函數，我們提取這些知識后綜合得到了研究區滑坡敏感性與環境因子之間的關系（表1）。

利用從專家群里提取的知識和具體參數，建立定量描述滑坡敏感性與環境因子之間關系的隸屬度函數。

（1）由坡度引起的滑坡敏感性表示為：

fS（dij，S）=1.0（dij，S≥30）

exp-dij，S-30×0.8326202（dij，S<30）（6）

式中：dij，S為位置（i，j）的坡度。

（2）由斜坡類型引起的滑坡敏感性表示為：

fSS（dij，SS）=0.0（dij，SS=6）0.1（dij，SS=3）0.3（dij，SS=5）0.5（dij，SS=1）0.8（dij，SS=2）0.1（dij，SS=4）（7）

式中：dij，SS為位置（i，j）的斜坡形態類型。

（3）相對高差和滑坡敏感性之間的關系與斜坡類型相關，并通過斜坡類型發生作用。不同斜坡類型下由相對高差引起的滑坡敏感性定義為：

fRR（dij，RR）=fSS（dij，SS）×1.0（dij，RR≥400）exp-dij，RR-400×0.83262002（dij，RR<400）（8）

式中：dij，RR為位置（i，j）的相對高差，單位為m。

（4）由巖性引起的滑坡敏感性表示為：

fL（dij，L）=

1.0（dij，L=Ⅳ）

0.5（dij，L=Ⅲ）

0.2（dij，L=Ⅱ）

0.1（dij，L=Ⅰ）（9）

式中：dij，L為位置（i，j）的巖性類型。

（5）地點的構造條件對滑坡敏感性的影響通常與斜坡的坡度和坡向有關， 由構造和斜坡信息組合引起的滑坡敏感性定義為：

fSG（dij，SG）=0 （dij，ag-dij，as>90）

0（dij，d>dij，S）

exp-dij，d-dij，S×0.8326452×cos（dij，ag-dij，as）（dij，ag-dij，as≤90）且（dij，d≤dij，S）（10）

式中：dij，d是位置（i，j）的地層傾角;dij，ag是位置（i，j）的地層傾向;dij，S是位置（i，j）的斜坡坡度;dij，as是位置（i，j）的斜坡坡向。

（6）由多年平均降水量引起的滑坡敏感性定義見公式（3）。

（7）由土地利用類型引起的滑坡敏感性定義為：

fLU（dij，LU）=1（dij，LU≥9）exp-0.8362dij，LU-962（dij，LU<9）（11）

式中：dij，LU為位置（i，j）的土地利用類型賦值。

在得到以上7個環境因子組合之后，我們就可以將每個組合所計算出的模糊函數隸屬度值采用約束算術平均法來計算滑坡敏感性綜合值。在計算過程中，給各組合的權重是一樣的（朱阿興等，2004），其原因是我們認為約束后每種組合出現的機率大致類似。由于每個組合計算的滑坡敏感性值為0～1（含0和1），因此，通過約束算術平均法得到的綜合模糊滑坡危險性也為0～1（包括0和1）。

2.2.2 環境因子柵格圖層數據表征

研究區滑坡的環境因子及其數據來源見表2。由于環境因子柵格數據集中，相對高差信息和6類斜坡形態信息的提取難以直接通過ArcGIS軟件直接完成，所以需要分步驟來對這些信息進行GIS表征。對地形信息的計算主要分為3個步驟：①提取研究區山脊和山谷信息。山脊和山谷信息可以通過自動化的方式或手工數字化的方式完成，本文使用GIS中的網絡提取技術。②計算相對高差。具體算法為從山脊的每個像元（假設海拔高度為H1）沿水流流向向下追蹤，直到到達山谷區像元（假設海拔高度為H2）。兩者的高程差（即H1-H2）設置為沿此路徑（從山脊到山谷）上所有像元的相對高差（單位：m）。③相對高差插值。因為不能保證在上一步計算完成后，研究區內的每個像元都有相對高差值，因此采用鄰近插值方法，確保每個像元都有整個區域的相對高差。

斜坡形狀信息的提取分為3個子步驟：①提取研究區山脊和山谷信息。②確定斜坡形態類型。從山脊區的每個像元開始，沿著水流流向向下追蹤，直到到達山谷區的一個像元為止。記錄沿此路徑的所有高程值并生成剖面形態，根據坡度形狀分類確定沿此路徑的斜坡形態類型（圖7）。將得到的斜坡形態類型設置為沿此路徑（從山脊到山谷）上所有像元的斜坡形態類型。③對整個研究區進行斜坡形態信息插值。采用近鄰插值方法對上一步驟后未采集到斜坡形態信息的像元進行斜坡類型信息計算。

2.2.3 滑坡敏感性模糊推理

結合專家知識和滑坡環境因子對南澗地區滑坡敏感性進行模糊推理，推斷出的滑坡敏感性如圖10所示，可以劃分為4個區：①高值和高值相連類型區。連片的高值區域在國土規劃整治中應列入不宜開發區，也是滑坡隱患重點監視區。②低值和低值相連區。低值連片區在國土規劃整治中可以考慮合理開發利用，為滑坡隱患安全區。上述兩類區域是所有類型中占比最大的區域。③低值圍繞高值區。這類型地區就是安全區內的高滑坡風險隱患點，對隱患點要特別關注。④高值包圍低值區。大多數情況下，這類型區域中的低值區是沒有安全意義的，因為高值區發生的滑坡可能對低值區形成影響，因此低值區實際上可能也是潛在滑坡影響區，但是當被包圍的低值區面積較大足以緩沖滑坡影響時，則可以成為滑坡隱患區中的安全島，國土規劃整治中要分類考慮。

2.2.4 滑坡敏感性推斷的評價

為了評價模型的有效性，需要對模型結果進行檢驗。在檢驗方法中，Z值（Z-score）是衡量一組數據中的每一個數據與整組數據的平均值之間的偏離程度，即以標準差為單位表示一個具體數據到平均數的距離或離差。某個點的滑坡敏感性值等于平均值時Z=0，大于平均值時Z>0，小于平均值時Z<0。某個點的滑坡敏感性值越高表示滑坡的可能性越大，那些發生過滑坡或滑坡隱患點位置上的Z值越高越符合該位置容易滑坡的判斷。P值（P-Value）也是常用于衡量可信程度的一個遞減指標，P值越大，我們越不能認為樣本中變量的關聯是總體中各變量關聯的可靠指標。在許多研究領域，根據顯著性檢驗方法所得到的P值，通常認為P值為0.05是可接受錯誤的邊界水平，一般以P<0.05為有統計學差異，P<0.01 為有顯著統計學差異，P<0.001為有極其顯著的統計學差異。其含義是樣本間的差異由抽樣誤差所致的概率分別小于0.05、0.01、0.001。

本文通過檢查模型計算得到的歷史滑坡點敏感性值與整個研究區的滑坡敏感性平均值是否不同來評價本方法的性能，用Z值來測試差異的統計顯著性。因為研究區DEM是根據1978年制作的地形圖創建的，因此對收集到的1978—2000年的65次歷史滑數據進行整理和定位，計算得到南澗地區歷史滑坡點敏感性Z值為4.1，相應的P值遠遠小于0.001。這表明計算出的滑坡敏感性值是滑坡發生的良好指標。

通過將滑坡敏感性與其分級相結合，來進一步評價南澗地區滑坡敏感性推斷的有效性。采用自然斷點法對滑坡敏感性綜合值進行分級，根據分級結果將滑坡敏感性劃分成5個等級：極低（0.0～0.001）、較低（0.001～0.051）、中等（0.051～0.394）、較高（0.394～0.557）和極高（0.557～1.0）。對滑坡敏感性分級的目的是觀察不同滑坡敏感性等級的滑坡密度差異，來進一步評價基于GIS和專家知識的滑坡敏感性模糊邏輯推斷效果。從表3可以看到一個明顯的趨勢，滑坡敏感性水平的增加與研究時段內有記錄的野外滑坡事件密度增加有關。滑坡敏感性等級為極低和較低的地區沒有發現歷史滑坡記錄，滑坡敏感性等級為中等地區滑坡密度非常低，其滑坡密度約為敏感性等級為較高區域的1/4，為敏感性等級為極高區域的1/10。

2.3 模型在鳳慶—昌寧地區的應用

將南澗地區滑坡敏感性與環境因素之間關系的知識移植到該研究區時，所有指標、參數都不變。鳳慶—昌寧地區的滑坡敏感性如圖11所示，總體看，本區域內滑坡敏感性分布也有4類，即高值和高值相連類型區、低值和低值相連類型區、低值圍繞高值類型區和高值包圍低值類型區。我們用同樣的方法在鳳慶—昌寧地區檢測滑坡敏感性推斷的有用性。該區共觀測到290處滑坡（圖11），計算得出的Z值為8.93，相應的P值遠小于0.001。這表明計算得出的滑坡敏感性值是滑坡發生的良好指標，我們可以將南澗地區的專家知識外推到滇西南的另一個研究區，并且所建立的方法可以應用于滇西南更大范圍的研究區域。

同樣通過將滑坡敏感性與滑坡敏感性分級相結合，來進一步評價鳳慶—昌寧地區滑坡敏感性推斷的有效性。與已建立模型的南澗地區進行對比發現，本研究區也具有相似的滑坡密度差異，同樣在滑坡敏感性極低和較低區域沒有觀察到滑坡，滑坡敏感性較高地區歷史滑坡密度約是中等地區的4倍，敏感性極高地區約是中等地區的10倍。這一結果表明，計算得到的滑坡敏感性值可用于預測某地區未來發生滑坡的可能性。

3 討論

基于GIS和專家知識的滇西南地區滑坡敏感性模糊邏輯方法研究是為了克服當前云南地區滑坡敏感性研究成果中存在的部分缺陷和改進部分現有研究方法的不足，以充分識別區域固有的滑坡風險隱患和可能存在的安全島。

專家對當地滑坡敏感性與環境因素關系的認識是長期理論研究和實踐的結果，總體上認知較一致。所以，模型建立過程中，若被提取知識的專家隊伍有變化，相應的指標體系和模型參數會稍微有所差別，但不會有本質的不同。由于云南地區本身環境差異極為顯著，在向云南其它區域移植本方法時，需要重新組織相應區域的專家進行具體知識的提取，否則得出的結果可能與實際有較大偏離。

對滑坡敏感性綜合值的計算，充分考慮了地理環境固有的特性，采用約束算術平均法對評估地點的滑坡敏感性綜合值進行推斷，在很大程度上識別了理論上存在的地震滑坡安全區。這種方法不僅是本文研究結果與已有研究結果有很大區別的原因，在本質上也是對風險評價理論認識的完善的一種體現。傳統的風險評價更多地關注“風險”，實際上，對“安全島”的研究應該成為風險研究的一個重要組成部分。風險研究不但要盡量識別高風險隱患區，也要充分掌握安全島信息，這樣才能為國土規劃與整治提出更合理的建議。如果本文采用簡單的算術平均法進行滑坡敏感性綜合值計算，得到的低值區域范圍應該變小，相應的后續的滑坡敏感性分級結果也會有變化。

滑坡敏感性分級對區域風險減輕有重要信息支撐，不同分級方法帶來的結果會存在較大差別。本文采用的自然斷點法是根據區域滑坡敏感性推斷值的一種分類，這種分類不受人為知識的干擾，完全是基于數據本身的一種客觀分級。若采用類似三峽研究區的主觀定義分級方法，結果會有不同，相應的各滑坡敏感性水平區域的范圍、滑坡密度都會發生變化。

4 結論

本文選取滇西南的南澗和鳳慶—昌寧兩個研究區，開展基于GIS和專家知識的滑坡敏感性模糊邏輯評價，并進行適用性的檢驗。研究結果統計檢驗顯示，南澗地區的Z值為4.1，相應的P值小于0.001，這表明，通過模型計算得到的滑坡敏感性值是該研究區滑坡事件的良好指標;鳳慶—昌寧地區的Z值為8.93，相應的P值小于0.001。根據2個研究區的滑坡敏感性分布情況，可以將區域滑坡敏感分布分為4種類型區：高值和高值相連類型區、低值和低值相連類型區、低值圍繞高值類型區、高值包圍低值類型區。

采用自然斷點法，根據研究區滑坡敏感性綜合值的分布，將滑坡敏感性劃分為5個等級：極低（0.0～0.001）、較低（0.001～0.051）、中等（0.051～0.394）、較高（0.394～0.557）和極高（0.557～1.0）。通過對比不同滑坡敏感性水平區域歷史滑坡密度的不同來評價模型的物理效能。滑坡敏感性等級為極低和較低的地區沒有發現歷史滑坡記錄，滑坡敏感性等級為中等地區的滑坡密度非常低，約為滑坡敏感性等級屬于較高區域的1/4，為滑坡敏感性等級屬于極高區域的1/10。這表明計算得到的滑坡敏感性值可用于預測某地區未來發生滑坡的可能性。在南澗地區建立的滑坡敏感性模型可以用于滇西南其它地區的滑坡敏感性推斷。

參考文獻：

丁星妤，戴塔根，包從法，等.2011.云南滇中地區地質災害防治區劃[J].中國地質災害與防治學報，22（2）：69-75.

杜玉龍，方維萱.2009.云南省東川銅礦區主要地質災害與致損機制防控[J].礦產與地質，（5）：480-486.

胡金，李波，唐立梅.2007.云南省魯甸縣地質災害特征與成因研究[J].地質災害與環境保護，（4）：15-19.

胡金，李波，楊艷鋒.2008.GIS 在云南魯甸縣地質災害易發性分區中的應用[J].災害學，（1）：73-75，87.

紀甲子，陳愛兵，李俊，等.2010.云南省劍川縣地質災害調查及成因分析[J].云南地質，（4）：471-474.

李英，馮彥，周火艷.2009.怒江干流（云南段）滑坡災害危險性分析[J].云南地理環境研究，21（6）：18-21.

李志斌，鄭成德.2000.滑坡、泥石流危險度評判的灰色模式識別理論與模型[J].系統工程理論與實踐，（5）：128-132.

劉麗，王士革.1995.云南昭通滑坡泥石流危險度模糊綜合評判[J].山地研究，14（4）：261-266.

呂勇，黃晨暉，陳陣.2010.云南文山縣地質災害易發程度分區評價[J].地質災害與環境保護，（4）：24-27.

錢晶，王瑞兵.2009.云南省祥云縣地質災害易發分區研究[J].昆明冶金高等專科學校學報，（5）：13-18.

孫黎麗，李波，劉江波.2007.云南省大關縣泥石流形成條件及防御對策研究[J].資源環境與工程，（4）：416-419.

唐川，周鉅，朱靜.1994.云南崩塌滑坡危險度分區的模糊綜合分析法[J].水土保持學報，（4）：48-54.

唐川.2004.金沙江流域（云南境內）山地災害危險性評價[J].山地學報，22（4）：451-460.

陶云，唐川，段旭.2009.云南滑坡泥石流災害及其與降水特征的關系[J].自然災害學報，18（1）：180-186.

田志萌，張淵，郭睿，等.2011.云南省曲靖市麒麟區地質災害特征及防治措施[J].西部探礦工程，（11）：121-123，127.

萬石云，李華宏，胡娟.2013.云南省滑坡泥石流災害危險區劃[J].災害學，28（2）：60-64.

謝洪，鐘敦倫，何一平，等.2007.金沙江下游云南小江流域山地災害綜合區劃[J].山地學報，25（5）：622-628.

顏春達，溫欽舒，武紹周.2017.東川地質災害特征淺析[J].工程勘察，S（1）：154-157.

尹詩琪，王冬冬，徐星安，等.2012.云南省思茅區地質災害發育特征及防治對策[J].四川地質學報，（3）：339-342，363.

于豐澤，武蕾.2012.云南大理滑坡應急治理措施效果分析[J].四川建筑，32（4）：108-112.

翟倩倩，吳加權，葉飛，等.2016.云南哀牢山中段滑坡災害多指標預警研究[J].昆明理工大學學報（自然科學版），41（4）：38-44.;

張超，陳艷，張宇飛，等.2016.基于多元線性回歸模型的云南昭通地質災害易發性評價[J].水文地質工程地質，（3）：159-163.

周松林，談樹成，蔣順德，等.2010.云南省保山市隆陽區地質災害空間分布規律及易發性分區與評價[J].地球與環境，（3）：351-356.

朱阿興，裴韜，喬建平，等.2006.基于專家知識的滑坡危險性模糊評估方法[J].地理科學進展，25（4）：1-12.

Aleotti P，Chowdhury R.1999.Landslide hazard assessment：summary review and new perspectives[J].Bull Eng Geol Environ，58：21-44.

Alexander D E.2008.A brief survey of GIS in mass-movement studies，with reflections on theory and methods[J].Geomorphology，94（1-3）：261-267.

Atkinson P M，Massari R.1998.Generalized linear modeling of landslide susceptibility in the Central Apennines，Italy[J].Computers & Geosciences，24（4）：373-385.

Brabb E E.1984.Innovative approaches to landslide hazard and risk mapping[C]//Proceedings of the Fourth International Symposium on Landslides，Proc 4th International Conference and Field Workshop on Landslides.Publ Tokyo：Japan Landslide Society Japan，17-22.

Burrough P A.1989.Fuzzy mathematical methods for soil survey and lands evaluation[J].J Soil Sci，40（3）：477-492.

Carrara A，Cardinali M，Detti R，et al.1991.GIS techniques and statistical models in evaluating landslide hazard[J].Earth Surf Process Landf，16：427-445.

Carrara A，Pike R J.2008.GIS technology and models for assessing landslide hazard and risk[J].Geomorphology，94（3-4）：257-260.

Carrara A.1988.Landslide hazard mapping by statistical method：a “black-box” model approach[C]//Siccardi F，Bras R L.Natural Disasters in European Mediterranean Countries，Colombella，Perugia，Italy，205-224.

Chung C F，Fabbri A G，van Westen C J，1995.Multivariate regression analysis for landslide hazard zonation[C]//Carrara A，Guzzetti F.Geographical Information Systems in Assessing Natural Hazards.Dordrecht，The Netherlands：Kluwer Academic Publishers，107-133.

Dai F，Lee C F.2002.Landslide characteristics and slope instability modeling using GIS，Lantau Island，Hong Kong[J].Geomorphology，42（3-4）：213-228.

Donati L，Turrini M C.2002.An objective method to rank the importance of the factors predisposing to landslides with the GIS methodology：application to an area of the Apennines （Valnerina; Perugia，Italy） [J].Eng Geol，63（3-4）：277-289.

Ermini L，Catani F，Casagli N.2005.Artificial neural network applied to landslide susceptibility assessment[J].Geomorphology，66（1-4）：327-343.

Fisher P.1989.Knowledge-based approaches to determining and correcting areas of unreliability in geographic databases[C]//Goodchild M，Gopal S.Accuracy of Spatial Databases.Taylor & Francis，London，45-54.

Fourniadis I G，Liu J G，Mason P J.2007.Landslide hazard assessment in the Three Gorges area，China，using ASTER imagery：Wushan-Badong[J].Geomorphology，84（2）：126-144.

Guzzetti F，Reichenbach P，Cardinali M，et al.2005.Probabilistic landslide hazard assessment at the basin scale[J].Geomorphology，72（1-4）：272-299.

Hudson B D.1992.The soil survey as paradigm-based science[J].Soil Sci Soc Am J，56：836-841.

Lan H X，Zhou C H，Wang L J，et al.2004.Landslide hazard spatial analysis and prediction using GIS in the Xiaojiang watershed，Yunnan，China[J].Eng Geol，76（1-2）：109-128.

Lee S，Choi J.2004.Landslide susceptibility mapping using GIS and the weight-of evidence model[J].Int J Geogr Inf Sci，18：789-814.

Liu J G，Mason P J，Clerici N，et al.2004.Landslide hazard assessment in the Three Gorges area of the Yangtze River using ASTER imagery：Zigui-Badong[J].Geomorphology，61（1-2）：171-187.

Luger G F.2005.Artificial intelligence：Structures and strategies for complex problem solving[M].New York：Addison-Wesley，903.

MacMillan R A，Pettapiece W W，Nolan，et al.2000.A generic procedure for automatically segmenting landforms into landform elements using DEMs，heuristic rules and fuzzy logic[J].Fuzzy Sets Syst，113（1）：81-109.

Oguchi T.1997.Drainage density and relative relief in humid steep mountains with frequent slope failure[J].Earth Surf Process Landf，22（2）：107-120.

Remondo J，Oguchi T.2009.GIS and SDA applications in geomorphology[J].Geomorphology，111（1-2）：1-3.

Shi X.2002.A case-based reasoning approach to fuzzy soil mapping[D].Madison，Wisconsin：University of Wisconsin.

Van Westen，C J，van Duren I，Kruse，H M G，et al.1993.GISSIZ：Training package for geographic information systems in slope instability zonation[M].Enschede，The Netherlands：ITC Publication No.15，ITC.

Zhu A X，Wang R X，Qiao J，et al.2004.Mapping landslide susceptibility in the Three Gorges area，China using GIS，expert knowledge and fuzzy logic[M]//Chen，Yangbo.GIS and remote sensing in hydrology.Water Resources and Environment，IAHS Publication 289 （IAHS Red Book），Wallingford，UK：International Association of Hydrological Sciences，385-391.

A Fuzzy Logic Modeling of Landslide Susceptibility Mapping in SouthwestYunnan Province Based on GIS and Expert Knowledge

BAI Xianfu1，2，DAI Yuqian1，YE Liaoyuan1，NIE Gaozhong3，XU Shuo2，LUO Weidong2，YU Jiang2，XU Xin2

（1.Faculty of Geography Science，Yunnan Normal University，Kunming 650050，Yunnan，China）

（2.Yunnan Earthquake Agency，Kunming 650224，Yunnan，China）

（3.Institute of Geology，China Earthquake Administration，Beijing 100029，China）

Abstract

In order to fully identify and effectively reduce the risk of landslide hazards，we presented an approach to landslide susceptibility mapping in southwest Yunnan Province based on the expert knowledge.The approach was tested in two study areas in southwest Yunnan：Nanjian（about 470 km2）and Fengqing-Changning（about 2 300 km2）.The performance of our approach was evaluated by examining if the mean value of the computed susceptibility values at landslide sites was statistically different from that of the entire study area.A Z-score test was used to examine the statistical significance of the difference.The computed Z-score for the Nanjian area was 4.1 and the corresponding P-value was less than 0.001.This suggested that the computed landslide susceptibility values were good indicators of landslide occurrences.In the Fengqing-Changning study area，the computed Z-score was 8.93 and the corresponding P-value was less than 0.001.In addition，we divided the susceptibility value into five levels by the Natural Break Point method.The result sets like：very low（0.0-0.001），low（0.001-0.051），moderate（0.051-0.394），high（0.394-0.557）and very high（0.557-1.0）.No landslides were found in areas of very low and low susceptibility.Landslide density was about four times higher in areas of very high susceptibility than that in the high susceptibility areas，and about 10 times as high as that in the moderate susceptibility areas.Results from these case studies suggest that our approach based on expert knowledge is workable in mapping landslide susceptibility and that its performance is maintained when it is applied to a new area.

Keywords：landslide susceptibility;expert knowledge;Fuzzy Logic modeling;Constrained Arithmetic Mean method;southwest Yunnan Province