四元低相關區非周期互補序列集構造
許成謙,李永雷,邢方園
(燕山大學 信息科學與工程學院,河北 秦皇島 066004)
0 引言
在多載波CDMA通信系統中互補序列(Complementary Sequence,CS)使用非常廣泛[1]。根據相關函數定義不同,有周期互補序列(Periodic Complementary Sequence,PCS)、非周期互補序列(Aperiodic Complementary Sequence,ACS)[2]。根據PCS、ACS的相關函數定義,可看出ACS包含PCS,因而ACS在實際通信系統中更具用途。非周期互補序列是由多個子序列構成的序列集,對于抑制通信系統中的多址干擾和多徑干擾有極其重要的作用,但其構造較難,滿足實際應用的較少,因而有必要對其深入研究。在通信系統中互補序列集(Complementary Sequence Set,CSS)不能支持大量的用戶,因此Fan等人在文獻[3]中提出了二元零相關區(Zero Correlation Zone,ZCZ)非周期互補序列集(ZCZ-ACSS)的概念。近年來人們在ZCZ-ACSS的構造方面研究較多且取得了較好效果。一類二元ZCZ-ACSS、三元低相關區(Low Correlation Zone,LCZ)非周期互補序列集(LCZ-ACSS)在文獻[4]中由Li等人利用一種特殊的正交序列集得以構造。Liu K等人在文獻[5]中通過交織法利用8位QAM正交序列集和P相正交序列集構造了一類最優的8位QAM零相關區非周期互補序列集。Liu T等人在文獻[6]中構造了具有低互相關特性的多重互補序列集,且集間非周期互相關幅度的最大值為P,通過組合后得到了一類幅度漸近最優的ACSS。在文獻[7]中,陳曉玉等人基于高斯整數正交序列集構造了具有理想的自相關性能和組內互補特性的一類最優的ZCZ-ACSS。近些年來,學者們進一步對ZCZ-ACS偶集、組間ZCZ-CS進行了研究。在正交矩陣偶的基礎上,文獻[8]提出了ZCZ-ACS偶集的構造方法。利用ZCZ序列集、整數集,白子祎等人在文獻[9]中構造了一類ZCZ在組內、組間均相等的PCSS。為進一步擴大CSS的集合大小,Liu B等人在文獻[10]中提出了低相關區準互補序列集的概念,并提出了低相關區準互補序列集的相關下界。Liu T等人在文獻[11]中構造了一種二元LCZ-ACSS,且序列集的參數漸近最優理論界限。目前為止,在文獻中并沒有對四元LCZ-ACSS的構造,因此本文構造的四元LCZ-ACSS能滿足通信系統一定的應用需求。
1 基本概念
定義1設兩個長度為L的復數序列a、b,a=(a0,a1,…,aL-1),b=(b0,b1,…,bL-1)。則這兩個序列的非周期相關函數Ca,b(τ)定義為
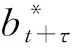
其中,t+τ=(t+τ)modL。若a=b,則Ra,b(τ)稱為周期自相關函數,記為Ra(τ)。顯然有
Ra,b(τ)=Ca,b(τ)+Ca,b(τ-L)。
定義2設一個L×L階矩陣H=[hk,t]L×L,令hk=(hk,0,hk,1,…,hk,L-1)表示矩陣H的第k行,其中0≤k≤L-1。對于矩陣H中任意兩行(或列)k1,k2,0≤k1≠k2≤L-1,hk1和hk2的互相關函數Rhk1,hk2(0)=0,則稱矩陣H為正交矩陣。
定義3設C={C0,C1,…,CM-1}是一個含M個序列的序列集,每個序列Cm包含N個長度為L的序列:
0≤m≤M-1,0≤n≤N-1,
Cm={Cm,0,Cm,1,…,Cm,N-1},
Cm,n=(cm,n(0),cm,n(1),…,cm,n(L-1))。
若序列相關函數:
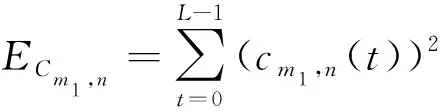
定義4定義二元到四元的映射如下:
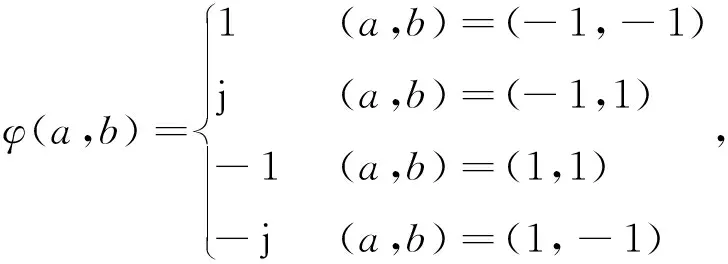
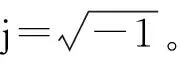
2 四元低相關區非周期互補序列集的構造
構造方法1:
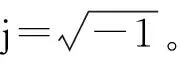
步驟二:取一個N×N階的二元完全非循環矩陣G=[gi,j]N×N,gi,j∈{-1,1}。
步驟三:選定兩個正整數Z,K,滿足Z/N,L=KZ,M=KN。
步驟四:當0≤m≤M-1,0≤n≤N-1,0≤t≤L-1時,取:
sm,n(t)=g?m/L」·Z+(tmodZ),n·q(mmodL),t,
Sm,n=(sm,n(0),sm,n(1),…,sm,n(L-1)),
Sm={Sm,0,Sm,1,…,Sm,N-1},
S={S0,S1,…,SM-1}。
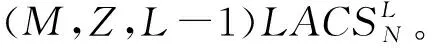
證明在S中任取Sm1,n,Sm2,n∈S,計算非周期相關函數如下:
g?m2/L」·Z+((t+τ)mod Z),n·q(m2mod L),t+τ=
m3=?m1/L」·Z+(tmodZ),m4=?m2/L」·Z+((t+τ)modZ)。分四種情況討論:
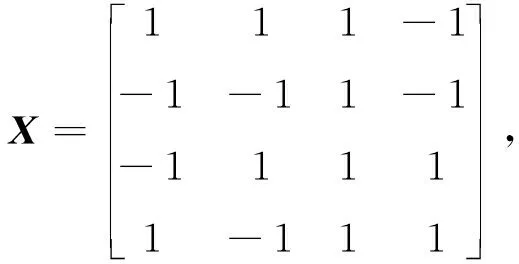
情況一,若m1=m2,0<τ 其中,k1=m1modL,k2=m2modL。 證畢。 構造方法1中使用了四元正交序列集和完全非循環矩陣,而四元正交序列集可以用文獻[12]的構造方法得到,完全非循環矩陣可以用文獻[13]的構造方法得到,故本文的構造方法是可以實現的。 例取一個4×4階二元正交矩陣如下: 按照文獻[12]的構造方法利用上述矩陣X可得到一個四元正交序列集Q={q0,q1,q2,q3}: q0=(-1,-j,-1,j),q1=(j,1,-j,1), q2=(j,-1,-j,-1),q3=(-1,j,-1,-j)。 給定一個3×3階二元完全非循環矩陣如下: S0={(0103);(2321);(0103)}, S1={(3212);(1030);(3212)}, S2={(3010);(1232);(3010)}, S3={(0301);(2123);(0301)}, S4={(2321);(0103);(0103)}, S5={(1030);(3212);(3212)}, S6={(1232);(3010);(3010)}, ? 本文所構造的四元低相關區非周期互補序列集的低相關區長度Z在滿足Z/N(N為子序列個數)條件下可靈活設定。低相關區非周期互補序列包含低相關區周期互補序列的性質,因此在實際通信系統中具有更大用途。本文的構造方法是基于四元正交序列集和二元完全非循環矩陣,在實際通信系統中,這兩者都較易得到且存在較廣,從而可得到大量四元低相關區非周期互補序列集,進一步滿足多載波CDMA通信系統的需求。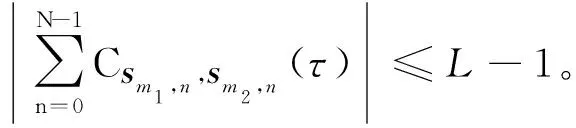
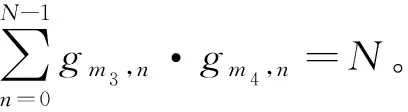
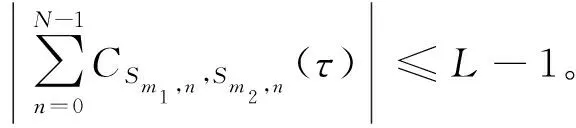
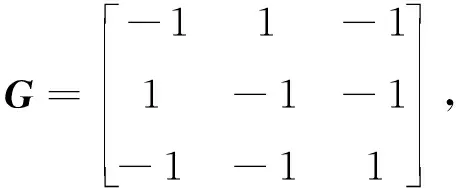
3 結束語

