從集中式到分布式的贏者通吃網絡:回顧與展望
齊一萌,金 龍
(蘭州大學 信息科學與工程學院,甘肅 蘭州 730000)
0 引言
一類能夠從一組輸入信息中選擇出最大值的競爭型神經網絡被稱為贏者通吃(Winner-Take-All,WTA)網絡[1],它是由神經元之間的橫向抑制形成的。WTA網絡作為k-WTA網絡的特例,已被廣泛應用于模式識別[2]、聯想記憶[3]、多智能體協同[4]以及認知現象模擬[5]等多種領域。Maxnet是傳統用于模擬WTA行為的神經網絡[6],它提供了一個離散形式的相互抑制的結構。從數據陣列中選擇最大值這一操作在許多領域都是至關重要的,如決策系統和競爭學習網絡[7]。為此,國內外學者開展了一系列研究,例如基于自組織算法的迭代神經網絡模型,該類模型主要適用于軟件實現[8]。輸入信息規模的擴張以及計算實時性的要求使得并行方法及可硬件實現的算法備受關注[9]。Lazzaro等人[10]設計了一系列緊湊的互補金屬氧化物半導體集成電路來實現WTA行為。Wawryn等人[11]引入一種基于電流源電路的可編程WTA神經網絡,并驗證了其有效性。然而,以上工作均面向靜態WTA問題設計,未考慮實際應用場景的動態特征。進一步地,Majani等人[12]將WTA網絡擴展到k-WTA網絡,然而只保證了模型的局部穩定性。此后,設計超大規模集成電路來執行k-WTA運算成為一個研究熱點[13]。Calvert等人[14]構建了一種Hopfield型神經網絡,并通過嚴格的穩定性分析證明了其能夠有效地識別序列中的最大分量。Tymoshchuk[15]根據輸入信號的動態移位設計了一個離散k-WTA神經電路,該電路硬件實現復雜度較低,且能在有限的迭代次數內收斂。此后,Tymoshchuk和Wunsch[16]設計了一種有限分辨率的連續k-WTA神經模型,其理論上能夠處理未知輸入并保證瞬時零誤差。Danciu 等人[17]介紹了一種具有O(n2)結構復雜度的遞歸神經網絡,其中n表示輸入的數量。然而,該網絡需通過將其增益參數設定為無限大以確保k-WTA系統的正確運行。
出于對模型結構的優化,文獻[18-19]分別首次實現WTA或k-WTA問題向線性規劃(Linear Programming,LP)和二次規劃(Quadratic Programming,QP)的轉化。進而投影神經網絡、對偶神經網絡、動態神經網絡等被陸續開發并應用[18,20],同時在多樣化激勵函數的引入[21]、收斂速率的提升[22]等方面均做出了改進。為進一步簡化模型復雜度,多種單狀態變量的連續/離散型時間遞歸神經網絡被構建。這些模型[18-22]在處理時不變輸入的k-WTA 操作時表現出有限時間收斂性能,但處理時變輸入時存在滯后誤差,需要通過設置足夠大的參數來緩解這一現象。Ferreira等人[23]針對變量有界的LP問題,構造了一個k-WTA神經網絡(k-WTA Neural Network,kWNN),將問題的解轉化為所設計神經網絡的平衡集,并證明了所構建網絡的收斂性。前述研究的k-WTA問題及求解算法均明確指定k的數值,而文獻[24]的工作突破了這一限制,提出了一種基于梯度下降法的kWNN模型,實現了k值的動態確定。然而,包含上述工作在內的算法仍存在一些挑戰。首先,在處理本質上具有動態特性的問題時,這些方法忽略了內部動態參數隨時間的變化趨勢,使得它們預測能力不足,從而導致每一時刻所得解與理論解之間存在滯后誤差。這種誤差是不可忽略的,且會隨時間累積影響任務的執行精度。其次,上述神經網絡的設計均未考慮去噪措施,因此在噪聲干擾下,神經網絡的性能會顯著下降。而在實際的k-WTA問題求解過程中,干擾是不可避免的,這一定程度上限制了現有算法在復雜環境中的應用。鑒于此,作者已有的工作[25]基于具有良好抗噪性能的零化神經網絡[26]、牛頓積分增強型網絡[27]、飽和約束神經動力學模型[28]等,汲取這些網絡設計中的優勢結構,從神經網絡求解能力與魯棒性兩個層面入手開發用于k-WTA操作的新型神經網絡。
此外,隨著計算能力與存儲能力的提升,工業控制規模的不斷擴大,從分布式的角度處理問題的方法備受關注。迄今為止,包括上述成果在內的k-WTA研究大多以集中式方式實現。換言之,上述工作未考慮任何拓撲約束,無法直接應用于具有任意拓撲結構的連通圖。Li 等人[29]首次明確考慮了群體間的交互拓撲結構,并提出了一種分布式WTA模型來解決群體系統中的動態競爭問題。基于這一研究,Zhang等人[30]從QP形式的k-WTA問題入手,直接構建了一種分布式k-WTA模型,具有良好的容錯性與全局收斂性。這些成果點明了研究分布式k-WTA網絡的必要性,為后續基于k-WTA思想的廣泛應用奠定了基礎。
本文回顧了k-WTA網絡的發展及求解算法的研究現狀,并以分布式k-WTA網絡的構建為核心,介紹了包含多機器人系統在內的應用前景。
1 問題建模與算法構建
針對理論實現或應用場景中不同的側重點,k-WTA可被表述為各種不同的形式[31],進而設計不同方案來求解該操作。本文給出一種典型的數學映射來表示泛化的k-WTA屬性:
(1)
式中,u∈m和y∈m分別表征k-WTA系統的輸入和輸出信息;ui和yi分別為u和y的第i個元素;k表示期望獲取的輸出信息y最大值的個數。從數學角度而言,k-WTA反映為從數據陣列中選擇最大值的操作。文獻[18]已經證明式(1)可被重新規劃為一個LP問題:
最小化 -uT(t)y(t),
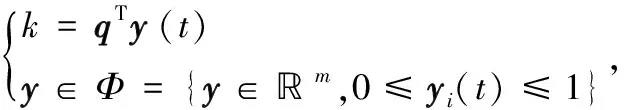
(2)
式中,上標T為轉置運算符;q=[1,1,…,1]T∈m。類似地,式(1)可被等價轉化為一個QP問題[19]:

(3)
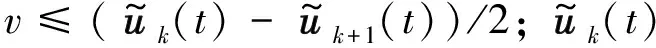
在已有的成果中,若干有效的遞歸神經網絡模型被陸續構建用于解決式(2)或式(3)。例如,Xia等人[32]針對式(2)提出了一種源對偶神經網絡:
其中,x∈為放縮參數;Γ1(·)為分段線性激勵函數:
Gu等人[18]針對式(2)提出了一種投影神經網絡:
其中,x∈;δ>0為放縮參數;ε2為一個正常數;Γ1(·)的定義同前所述。
文獻[19]針對式(3)提出了一種簡化的對偶神經網絡:
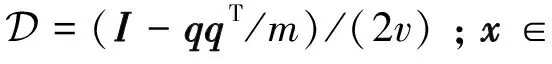
y=Γ3(u-qx),
其中,x∈;δ>0為放縮參數;Γ2(·)和Γ3(·)均定義為單調且不連續的激勵函數:
然而,上述算法存在兩方面的缺陷:一是這些算法面向靜態k-WTA而構建,不適用于求解實際動態問題或具有動態特性參數的問題,由于其沒有考慮動態參數的導數信息,會帶來較大的滯后誤差;二是這些模型均未考慮包括截斷誤差、舍入誤差等設備誤差,以及環境干擾在內的噪聲影響,使得模型的求解精度無法得以保證。考慮到以上算法所面臨的挑戰,文獻[25]提出了一種魯棒kWNN模型。首先將式(3)所示的QP問題等價轉化為非線性方程組D(t)z(t)-ρ(t)=0。該方程具體的參數構成為:
(4)
其中E(t)=[Im×m;-Im×m];λ(t)∈和η(t)∈2m分別為式(3)中等式和不等式約束對應的Lagrange乘子;
s(t)=[q;0m]為由1和0組成的向量;(t)=s(t)-E(t)y(t);ι→0+∈2m。進而所構建的kWNN模型被表示為:
(5)


2 分布式通信結構實現

Olfati-Saber等人[34]在一致性算法方面做出了開創性的工作,分析了不同通信拓撲和時延下穩定收斂的一致性問題。之后的工作[35]研究了移動網絡的動態平均一致性協議,并構建了比例型及比例積分型一致性濾波器,這為該領域的研究人員提供了開拓性的思路。基于這些工作,Freeman等人[36]設計了一種改進的比例積分算法,在提高收斂速度和穩定性的同時,完全消除了一致性中的穩態誤差。此后,相關探索層出不窮,涌現了多方面的成果[37]。此外,狀態飽和、輸入飽和、輸出飽和的一致性問題也成為研究熱點。例如,文獻[38]研究了輸入飽和對一類線性多智能體系統的影響,并在此情況下實現了分布式自觸發共識。進一步,考慮實際通信情況,輸入飽和與狀態飽和兩種約束下的一致性被研究[39],并提供了一致性算法穩定性的充分條件。文獻[40]研究了輸出飽和的一致性問題,主要考慮了由測量單元的范圍限制帶來的有界非線性特性。另一個值得回顧的是文獻[41]所開展的工作,其研究了包括非理想通信鏈路的線性協議、具有輸入飽和的非線性協議等在內的多種一致性協議。

(6)

為降低通信消耗并保持系統的可擴展性與穩定性,在成本溢出或參與者出現通信中斷或阻塞的情況下,需要及時進行拓撲切換。Jin等人[43]在文獻[44]的基礎上給出了一種基于切換拓撲的一致性濾波器:
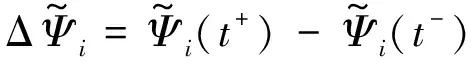
3 基于k-WTA的多機器人競爭協同
多機器人系統因具有良好的容錯性、高效性和可擴展性[45],適用于處理各種復雜和不可預測的任務[46],如運動規劃[47]、搜索和救援行動[48]、自動控制[49]等。受生物/社會群體內部行為機制的啟發,多機器人系統的協同行為主要包括合作和競爭兩種狀態,且二者都具有一定的優勢和廣泛的應用。例如基于合作行為開展的集群編隊、緊急救援等研究[50],基于競爭行為開展的資源調度、動態圍捕等。合作可以使多機器人系統在復雜環境中輕松工作,并提高任務的成功率,而競爭型協同可初步為系統篩選優秀的個體,在節能和降低成本方面有顯著的優勢。相較于針對多機器人合作展開的研究熱潮[51-52],競爭行為的研究成果較少,其中一個廣為人知的方法是強化學習[53-54]。該類方法尤其適用于多機器人系統,這是因為基于強化學習的方法在處理現實環境的不確定性、信息不完全性、分布式學習等問題方面有著突出的優勢。然而,它們仍然面臨著巨大的挑戰。首先,這類方法的實現依賴于大量的數據,帶來巨大的計算量以及嚴重的時間/空間資源消耗,不適合多機器人實際控制場景[55]。其次,雖然這些方法可以在仿真或軟件中成功通過測試,但應用于動態且不可預測的真實環境中時,強化學習采用的試錯策略[56]會給機器人造成巨大的損失和高昂的成本。再而,針對機器人的強化學習很難設定通用的獎勵函數,對于不同的任務場景需要設計不同的函數進而不斷訓練模型,使得應用強化學習的機器人系統的泛化性大打折扣。鑒于此,從分布式控制的角度實現多機器人協同,可避免上述問題,弱化對環境信息的需求,從而降低多機器人系統的負擔,這是值得深入探索與研究的新思路。
3.1 多機器人系統協同方案
現階段基于k-WTA的多機器人分布式協同相關的研究已取得了若干成果,如文獻[25,42,57-58]。具體地,文獻[58]面向可被建模為質點的機器人群體,如輪式機器人等,研究了一種分布式競爭模型,其中機器人的運動學和動力學特性可被忽略。具體構建k-WTA指標為:
式中,φi和φt分別代表第i個機器人和目標物的位置。第i個機器人的運動控制動力學被表示為:

(7)
式中,£>0是與收斂速度相關的變量,表示連接機器人與目標之間距離與機器人速度變化的反饋增益。顯然,輸出yi=1所對應的第i個機器人被用于執行追蹤任務,而輸出yi=0所對應的機器人未激活,靜待下一任務目標的來臨。
對多機器人系統的研究不應局限于輪式機器人,帶有機械臂的機器人已廣泛應用于工業制造領域,包括設計、搬運和抓取等場景,尤其在涉及精密任務時,占據著不可取代的地位。例如,航天飛機使用Canadarm來操縱有效載荷。因此,文獻[42]將分布式競爭協同行為推廣至帶機械臂的多機器人系統來完成基于k-WTA的任務分配。考慮一個結構信息均為時變參數的n自由度冗余機械臂,其關節角度為θ(t)=[θ1(t);θ2(t);…;θn(t)]∈n;末端執行器的笛卡爾坐標為r(t)∈p且定義期望軌跡為rd(t)∈p,則運動學方程被表示為Ω(θ(t))=r(t)。其中,Ω(·)代表非線性映射函數,對于確定結構的機器人,其相關參數和設置是已知的。對上式兩邊求導可得:
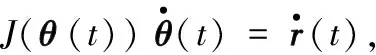
式中,J(θ(t))=?Ω(θ(t))/?θ(t)∈p×n為雅可比矩陣;為關節速度向量;為r(t)對時間的導數。注意系數矩陣J在t∈[0,T]的任意時刻都必須是非奇異的,以確保可被求解,其中T為完成期望軌跡的執行時間。因此,假設使用由m個機器人組成的多機器人系統進行協同作業,則需為每個機器人分配期望軌跡,此時每個機器人應滿足:
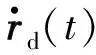
其反映了每個機器人規劃的運行路徑與期望運動路徑之間的距離。繼而,在接收到的驅動指令信號的激勵下,每個機器人的速度表示為:

結合實際應用場景,若考慮冗余度機器人的避障能力以及關節速度的安全取值域,則會涉及到對于關節角度、關節角速度、關節角加速度等的約束。這些均可以看作是對于如上驅動指令信號額外考慮飽和約束/映射函數[43]。
3.2 分布式k-WTA協同方案
以式(5)~式(7)為例,構建有限通信環境下用于多機器人競爭協同的分布式k-WTA協同方案為:

y={z}m,
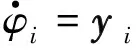
(8)
該系統具體應用步驟如下:
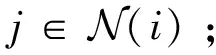
② 初始化相關參數D,ρ(t)和z。
③ 獲取φi和φt的信息。
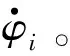
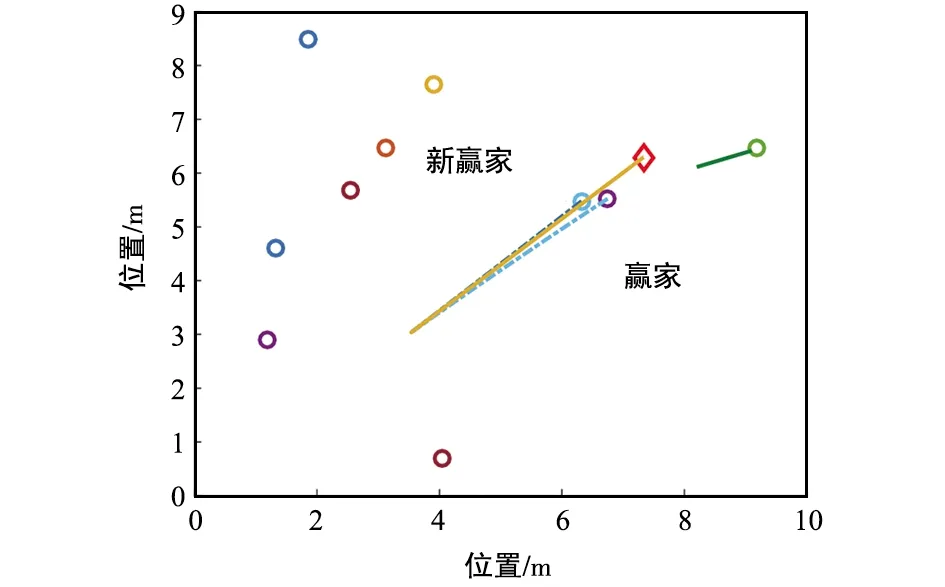
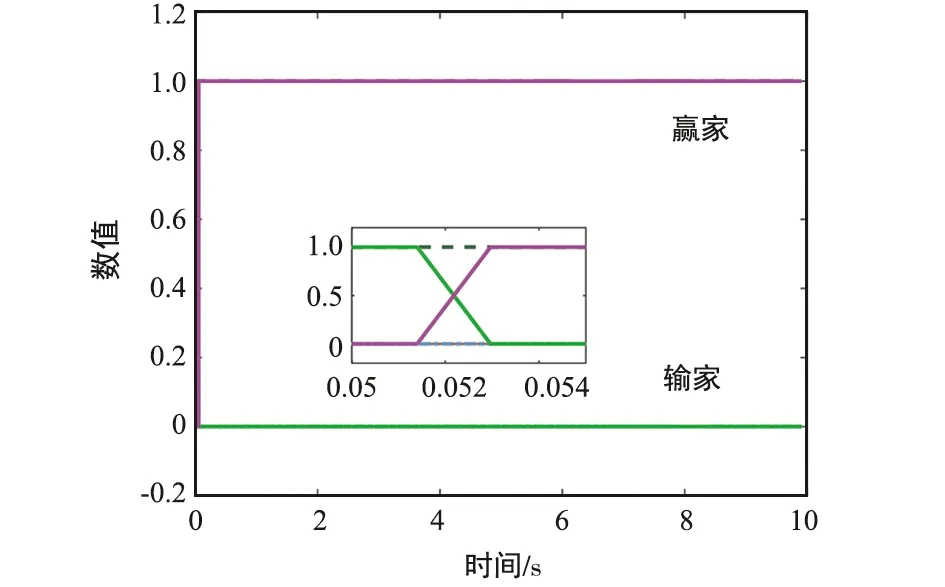
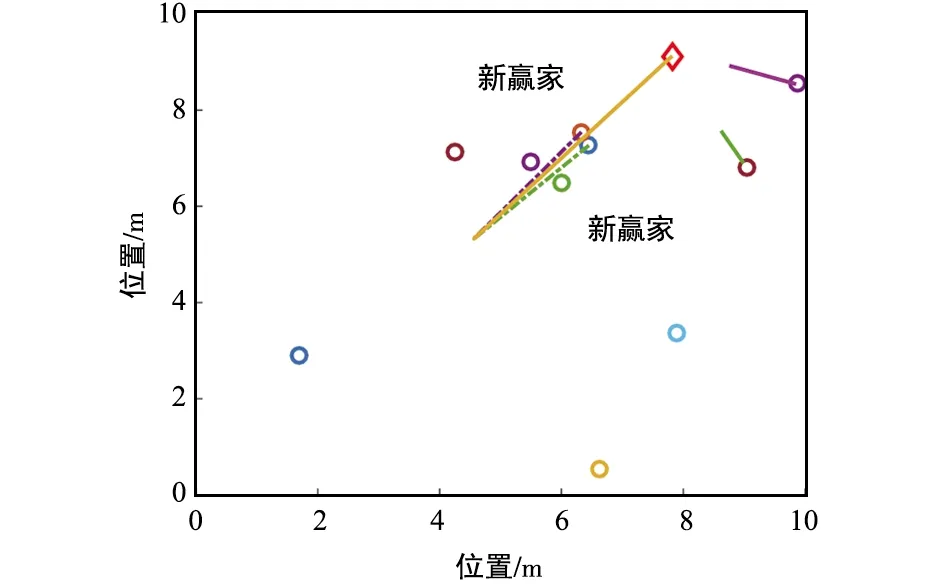
⑥ 判斷條件‖yi(φi-φt)‖2 根據分布式k-WTA協同方案(8)及上述實現步驟,可進行相關的仿真驗證,結果如圖 1~圖 6所示。 圖1 一個贏家發生替換時,多機器人系統運動軌跡-階段ⅠFig.1 Motion trajectory of the multi-robot system with a winner replaced-Stage Ⅰ 圖2 一個贏家發生替換時,多機器人系統運動軌跡-階段ⅡFig.2 Motion trajectory of the multi-robot system with a winner replaced-Stage Ⅱ 圖3 分布式k-WTA網絡的輸出Fig.3 Outputs of the distributed k-WTA network 圖4 兩個贏家發生替換時,多機器人系統運動軌跡-階段ⅠFig.4 Motion trajectory of the multi-robot system with two winners replaced-Stage Ⅰ 圖5 兩個贏家發生替換時,多機器人系統運動軌跡-階段ⅡFig.5 Motion trajectory of the multi-robot system with two winners replaced-Stage Ⅱ 圖6 分布式k-WTA網絡的輸出Fig.6 Outputs of the distributed k-WTA network 考慮到k-WTA思想在社會學以及經濟學等多學科領域的研究價值,以及其在包含多機器人系統在內的群體系統協同中的重要理論意義與廣闊應用前景,面向k-WTA操作的高性能求解算法開發和分布式網絡構建技術仍需不斷突破,且基于k-WTA網絡的應用場景有待挖掘。例如,如下問題可以作為一些探索的方向: (1) 開展離散計算模型或算法的研究 一方面,針對k-WTA操作的研究大多基于連續模型。盡管為了在數值設備上實現連續時間模型,已經有各種由數值差分公式導出的數值離散方法。然而,從數據時間定位的角度來看,這些方法大多不適用于處理時變問題,甚至是不可行的。例如,Matlab 中常用求解微分方程的工具“ode15s”,其求解基于龍格庫塔方法,但是該方法在使用過程中不僅需要使用當前時刻的信息量,同時需要未來時刻的信息作為輸入。然而每一個未來時刻的信息在當前計算時是不可知的,也即此時待求解系統為非因果系統[59-60]。因此,選取一個適合連續時間模型離散化的數值微分公式是得到符合因果律的計算方法的關鍵。另一方面,實際環境下機器人之間的通信是數字技術驅動的,并未涉及連續時間信號的交換。因此,連續模型對于直接處理信號發送、傳輸、接收等一系列離散信息操作效率較低。 (2) 開展復雜環境下分布式一致性協議的研究 現有基于k-WTA的競爭工作所考慮的拓撲大多為固定的,導致其在實際環境中的應用受到限制。明確而言,由于整個系統(或參與者)的動態特性和有限的通信范圍,通信拓撲通常是需要隨時間而變化的。再者,復雜場景中的障礙/干擾或軟硬件設備和傳感器的任意形式故障等問題可以看作是對系統施加了不可預測的物理約束,這很可能導致通信網絡的中斷或強制切換[61-62]。當參與者間出現通信中斷時,拓撲的不可切換性為系統的平穩運行和應急處理造成了一定的威脅。因此,可變拓撲、切換拓撲,甚至事件觸發型拓撲[63],在分布式一致性協議的研究中都是高效且推薦使用的。此外,實際通信環境中信道增益、時延、非線性等問題為分布式一致性協議的建模、精確性、穩定性提出了更高的要求。 (3) 拓展分布式k-WTA網絡的應用 k-WTA思想在眾多領域均能夠發揮其獨特的優勢。在深度學習中,k-WTA學習規則作為一種競爭關系的學習規則,可用于無監督學習,具體為通過將網絡的某一層確定為競爭層,最終調整該層中響應值最大的神經元(競爭中獲勝者)對應的權值。此外,k-WTA學習規則可作為一種典型的聚類算法,通過訓練實現聚類中心向樣本信息中心的演變,即根據訓練對象的特征用于損失函數設計,一定程度上避免梯度平均帶來的問題,降低局部最小值的影響。除上述數學或科學領域外,其在社會學問題建模中也占據一席之地,如以意見動力學為代表的社會行為建模。k-WTA思想通常符合包括競選、競標、政策、輿論等在內的意見動態演變過程,因此考慮實際信息的不完全共享性利用分布式k-WTA網絡進行建模,可以有效預測和評價社會系統演變的趨勢。立足現實開放場景,挖掘并研究k-WTA思想及分布式k-WTA網絡的應用場景是有潛在價值的。 本文對贏者通吃網絡的建模、發展及求解算法的構造進行了詳細的回顧和討論。此外,以分布式贏者通吃網絡的研究為核心,給出了一種高精度且魯棒的分布式贏者通吃神經網絡算法。進而,以多機器人系統協同為實例,指出了贏者通吃網絡的應用前景。這些豐碩的成果極大促進了神經網絡理論、分布式網絡、機器人技術的發展,并在相關領域取得了極大的進展。最后,分析了現有研究中尚需關注的問題及有待進一步攻關的方向。

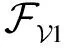
4 問題分析與研究展望
5 結論

