Qp 上分形多孔介質的流體動力學模型
2022-04-02 07:24:58吳波
浙江大學學報(理學版) 2022年2期
關鍵詞:模型
吳波
(南京財經大學應用數學學院,江蘇 南京 210023)
隨機多孔介質由復雜毛細網絡構成,因其上的流體(如油滴,水滴及乳狀液等)動力學模型在工業領域應用廣泛,廣受學者關注。 2016 年,KHRENNIKOV 等[1-2]提出了一種在超距空間上的數學模型框架,將液體滴流經多孔介質毛細網絡的動力學主方程轉化為在超距空間上的反應擴散擬微分方程。若記f(t,x)為液體滴在t時刻于毛細網中路徑x被發現的概率密度,則在其上的動力學模型由以下主方程刻畫:
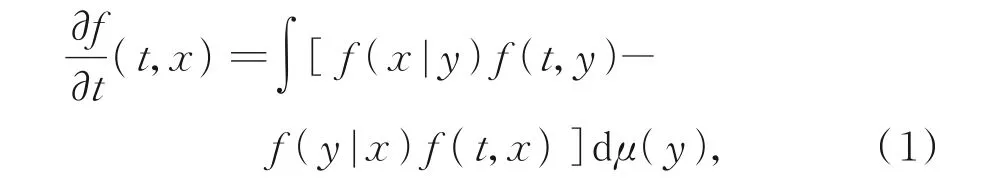
其中,μ為樹形毛細網絡上的概率度量,f(x|y)為液體滴從路徑y到路徑x的轉移密度。
如考察對稱形式的轉移密度

式(2)右端積分部分由超距空間的擬微分算子刻畫。
分形集上液體滴的流動及擴散模型在石油工業的二次采油技術設計中有重要應用[3-5]。本文的目的是將上述超距空間多孔介質的流體動力學模型推廣至分形集,并用文獻[6]中定義的擬微分算子Tα刻畫,給出滿足初始條件的液體滴在分形多孔介質上的流體動力學擬微分方程的確定解。
1 預備知識
首先,回顧p-adic 分析的一些基本知識[6-20]。
設p為素數,p的進數域為有理數域Q中的完備化Qp,并賦予p進范數|x|p,定義為


2 主要結果




3 結 論
研究了在分形集Γp,n上的一類反應擴散擬微分方程,利用蘇維宜[5]定義的擬微分算子Tα,得到了該類方程的定解,并研究了該形式解的收斂性。
感謝Andrei Khrennikov 教授對本文的指導!
猜你喜歡
童話王國·奇妙邏輯推理(2024年5期)2024-06-19 16:03:38
網絡安全與數據管理(2022年1期)2022-08-29 03:15:20
導航定位學報(2022年4期)2022-08-15 08:27:00
中學生數理化·中考版(2022年8期)2022-06-14 06:55:24
新世紀智能(數學備考)(2021年9期)2021-11-24 01:14:36
成都醫學院學報(2021年2期)2021-07-19 08:35:14
新世紀智能(數學備考)(2020年9期)2021-01-04 00:25:14
中學生數理化·七年級數學人教版(2020年10期)2020-11-26 08:24:50
數學物理學報(2020年2期)2020-06-02 11:29:24
光學精密工程(2016年6期)2016-11-07 09:07:19

