諧波減速器的傳動效率確信可靠性建模與分析

陳文彬 李曉陽 童邦安 李云 康銳

摘要：基于可靠性科學原理，在確信可靠性理論框架下，提出了諧波齒輪傳動效率確信可靠性建模與分析方法。考慮諧波齒輪傳動過程中的功率損耗以及影響傳動效率的多種外在因素，通過計算傳動效率與其閾值之間的距離，構建傳動效率裕量模型。開展多源不確定性分析與量化，構建傳動效率確信可靠性模型。針對傳動效率模型中的未知參數，給出了基于實測數據的極大似然估計方法。通過一個XB40-100諧波減速器的案例驗證了所提方法的實用性與可行性。結果表明，所提方法可以有效地將試驗數據與理論模型結合，進而準確計算諧波減速器在給定負載、轉速和溫度條件下的傳動效率。通過確信可靠性分析，發現適當提高負載扭矩、降低轉速或者提高環境溫度有助于提高傳動效率裕量及其可靠性。

關鍵詞：諧波減速器;確信可靠性;傳動效率;性能裕量;不確定性

中圖分類號：TB114.33;TH132.43

文獻標志碼：A

文章編號：10044523（ 2022）01-0237-09

DOI： 10.16385/j .cnki.issn.10044523.2022.01.026

引 言

諧波齒輪傳動技術是20世紀50年代隨著空間科學、航天技術的發展而產生的一種新的傳動技術[1]。它是在薄殼彈性變形的理論基礎上發展起來的，主要依靠中間撓性構件的彈性變形來傳遞運動。諧波齒輪機構具有結構簡單、體積小、重量輕、噪音低、承載能力高、傳動精度和傳動效率高等優點[2-3]，廣泛應用于空間技術、能源、機器人等領域。隨著應用領域的擴大和產品向著高質量長壽命發展的趨勢，對諧波齒輪傳動的可靠性提出了嚴格的要求。傳動效率是表征諧波齒輪傳動功能的重要性能指標之一[4]，因此，如何準確地計算諧波齒輪的傳動效率并開展可靠性分析，具有重要的實際意義。

為了計算諧波齒輪的傳動效率，很多學者開展了深入的研究。在諧波傳動效率的理論建模和仿真計算上，施祖康等[4]在實驗研究的基礎上，提出了一種傳動效率曲線計算方法，可以計算不同載荷條件下的傳動效率。陳樺等[5]分析了多種形式的諧波齒輪傳動的嚙合效率和波發生器效率，并提出了系統的傳動效率計算方法。Ianici等[6]針對一種雙波諧波減速器開展了傳動效率的實驗研究。楊連花[7]針對一種諧波行星復合減速裝置開展了傳動效率試驗，并與傳動效率的理論計算結果進行了對比分析。李德舉[8]圍繞著諧波傳動的功率損耗方面進行了分析與研究，提出了一種基于有限元軟件ABAQUS的功率損耗計算方法。肖京[9]通過ANSYS軟件分析并計算了諧波減速器中波發生器和輪齒嚙合的摩擦損耗。這些方法從理論角度給諧波齒輪傳動效率的計算提供了依據，但是目前已有的傳動效率計算方法還并不完善，除考慮諧波齒輪的制造參數外，大多僅考慮不同負載條件下的傳動效率計算。實際上，影響諧波齒輪傳動效率的因素種類很多，為此，很多學者開展了試驗研究。夏田等[10]針對工業機器人用諧波減速器，開展了正交試驗，定性地分析了潤滑方式、轉速和載荷對諧波減速器傳動效率的影響。李波等[11]針對空間潤滑諧波減速器開展了傳動性能試驗，研究了在超載條件和不同溫度條件下，固體潤滑和脂潤滑對柔輪一剛輪齒輪摩擦副的摩擦情況和對諧波減速器傳動性能的影響。李波[12]采用了交互正交試驗方法，進行了諧波減速器傳動性能熱真空試驗，研究了轉速、環境溫度、負載扭矩和潤滑方式等因素及其耦合作用對諧波減速器傳動效率的影響。Zhou等[13]基于諧波齒輪的傳動效率試驗，針對溫度、真空度、轉速和扭矩及其耦合對傳動效率的影響進行了方差分析。通過上述對諧波齒輪傳動效率的試驗研究可以發現，潤滑方式、負載、轉速和環境溫度是影響諧波齒輪傳動效率的主要敏感因素，但是目前已有的研究中大多是通過定性分析的方式探究這些敏感因素對傳動效率的影響，并沒有開展深入的定量研究。因此，還不能給出諧波減速器在實際工作和環境條件下的傳動效率模型。

在諧波齒輪的傳動過程中，往往期望其具有較高的傳動效率，傳動效率的下降代表著能量損耗的增多，且當傳動效率低至某一范圍時，會使得諧波齒輪的輸出功率難以驅動后續機構的動作，使得整個傳動系統發生失效，需要進行維修或更換。因此，在諧波齒輪的實際使用中，會給諧波齒輪的傳動效率設定一個下限值，即閾值。諧波齒輪傳動效率可靠性表征著其傳動效率滿足傳動要求的能力，可量化為諧波齒輪傳動效率高于其閾值的概率。近年來，有一些學者針對諧波齒輪機構的傳動效率開展了一些試驗，進行了可靠性建模與評估。李俊陽等[14-15]針對空間潤滑諧波減速器黏著磨損失效問題，建立了混合潤滑狀態下的黏著磨損模型，并以傳動效率為性能參數開展了加速壽命試驗和可靠性評估。官浩[16]構建了諧波減速器傳動效率的隨機退化模型并開展了諧波減速器的加速退化試驗，通過統計分析研究了空間諧波減速器的可靠性和壽命特征。目前對諧波齒輪傳動效率的可靠性研究還較少，大都通過試驗的方式評估諧波齒輪在某種工況條件下的可靠性和壽命指標，很少有文獻從理論模型的角度出發，搭建起諧波齒輪傳動效率的理論模型到可靠性模型的橋梁，并細致地考慮各種不確定性的影響，實現可靠性的量化。

為此，基于可靠性科學原理，在確信可靠性理論的框架下，本文對諧波齒輪傳動效率的可靠性開展研究，提出了諧波減速器傳動效率的確信可靠性建模與分析方法。首先，考慮諧波減速器傳動過程中的能量損耗以及影響傳動效率的多種外在因素的作用機理，構建諧波齒輪傳動效率的理論計算模型，并從性能裕量的角度，引入傳動效率的閾值，構建諧波齒輪傳動效率裕量模型。然后，針對裕量模型開展不確定性分析與量化，構建諧波齒輪傳動效率確信可靠性模型。接著，給出了基于諧波齒輪傳動效率實測數據的傳動效率模型中未知參數的極大似然估計，實現理論模型與試驗數據相結合。最后，本文針對一個XB40-IOO諧波減速器開展案例研究。該方法有助于計算諧波減速器在不同的工況和環境條件下的傳動效率及其可靠度，并通過對影響可靠度的敏感因素進行分析，實現對諧波減速器的設計和實際應用提供指導。

1 諧波減速器傳動效率可靠性建模

1.1 諧波減速器

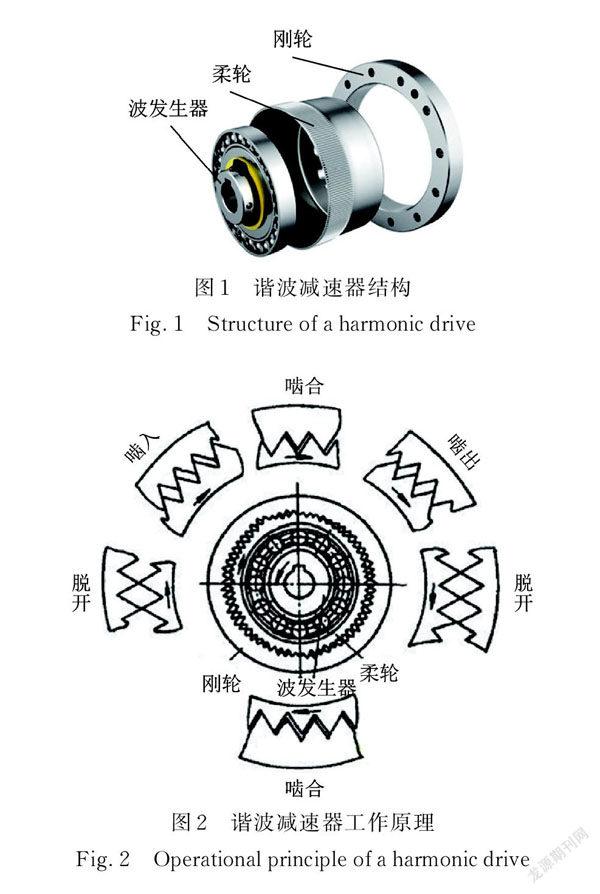
諧波減速器的構成主要包括三大零部件：剛輪、柔輪和波發生器。諧波減速器的結構如圖1所示。剛輪是一個剛性環狀內齒輪;柔輪是一個薄壁圓柱外齒輪，它和剛輪模數相同，但齒數一般比剛輪少兩個;波發生器是一個安裝在橢圓凸輪上的薄壁滾子軸承，外圓是橢圓形并隨著內圓旋轉，通過滾子作用產生旋轉變形，其最大直徑比柔輪內圓的直徑略大。諧波減速器工作時，由于波發生器的作用，柔輪產生變形，導致其長軸兩端的齒恰好與剛輪的齒完全嚙合，短軸處的齒則與剛輪的齒完全脫開。對于那些位于波發生器長軸和短軸之間的齒，則處于某些嚙人某些嚙出的過渡狀態。隨著波發生器的連續轉動，柔輪產生連續的彈性變形，使得柔輪與剛輪之間的齒不斷地重復“嚙入一嚙合一嚙出一脫開”這一過程，以此來傳遞嚙合運動，如圖2所示。本文考慮剛輪固定，波發生器主動，柔輪從動的諧波減速器。

1.2 傳動效率性能裕量建模

傳動效率表征著機構的機械能有效利用的程度，諧波齒輪傳動效率常用下式進行計算：式中 i為傳動比;Tout為諧波減速器的輸出軸扭矩;Tin為諧波減速器的輸入軸扭矩。

但是，在用公式（1）進行計算時，需要同時測量輸入軸扭矩和輸出軸扭矩，這使得公式（1）在實際應用時存在困難。

在諧波減速器動作過程中，輸入的機械能除轉化為有用功外，還存在各種能量損耗，主要包括：嚙合摩擦損耗We、由于嚙合力在諧波軸承中引起的摩擦損耗Wb和薄壁零件初變形所需徑向力在諧波軸承中所引起的摩擦損耗WF等[17]，如圖3所示。

考慮諧波減速器的能量損耗，其傳動效率可計算為：

王洪星[17]考慮諧波減速器的結構和動作原理，給出了諧波減速器動作過程中的有用功和上述三種能量損耗的理論計算方法，并針對剛輪固定，波發生器主動，柔輪從動的諧波減速器，對公式（2）進行了化簡，得到：式中 μ為諧波軸承中的當量摩擦因數;d為柔輪內徑;F為柔輪彈性變形力;M為負載扭矩;廠為齒面滑動摩擦因數;h為簡體厚度;R為剛輪齒高一半處直徑;a為輪齒壓力角。

通過公式（3）可以發現，諧波齒輪傳動效率除與諧波減速器組成部件的材料、尺寸參數外，只與負載扭矩相關。負載扭矩大，傳動效率高;負載扭矩小，傳動效率低。實際上，影響諧波齒輪傳動效率的因素有很多，比如潤滑方式、轉速、負載和環境溫度等[10-12]，這些因素影響傳動效率損失的主要機理為：

1）諧波減速器主要有三種潤滑方式：固體潤滑、脂潤滑和油潤滑。在含有潤滑的諧波減速器中，潤滑劑在齒輪表面會形成一層潤滑膜，該潤滑膜可以吸附磨屑微粒，進而達到降低摩擦，減小摩擦損耗的目的，不同類型的潤滑方式對減小摩擦損耗的程度有影響。

2）在含有潤滑的諧波減速器中，轉速的增加使得潤滑劑更容易被擠出，導致摩擦因數增大，摩擦損耗增大;此外，任何機械在旋轉過程中，都會對周圍空氣進行攪動，因此都存在風阻損耗，而且風阻損耗在減速器傳動總能量損耗中占有相當比例[18]。風阻損耗同樣也是通過摩擦損耗體現的，轉速越大，風阻損耗越大，摩擦損耗也越大;

3）諧波減速器負載的增加同樣會增加對潤滑劑的擠壓，使得潤滑膜變薄，進而使得摩擦因數增大。

4）溫度對于潤滑劑的流動性具有很大的影響，溫度升高，潤滑劑變軟，流動性變好，使得潤滑劑的黏度降低，進而降低了摩擦因數，減小摩擦損耗。

通過上述分析可知，潤滑方式、負載、轉速和溫度主要影響諧波減速器齒輪表面的摩擦因數。由于這些因素對摩擦因素影響的機理模型還不清晰，本文通過使用代理模型方式，將潤滑方式、扭矩、轉速和溫度對摩擦因素的影響考慮進去。令諧波減速器的齒面滑動摩擦因數滿足如下模型：

可靠性描述產品在規定條件下和規定時間內，完成規定功能的能力。康銳[19]總結凝練了可靠性科學的基本原理，其中第一條是“裕量可靠原理”，其含義為：產品的性能裕量決定著產品的可靠程度，性能裕量等于性能參數與其閾值間的距離。在本研究中，針對諧波減速器，以其傳動效率為性能參數，給定其失效閾值為ηth，當諧波齒輪傳動效率低于ηth時，諧波減速器的輸出功率較低，不能驅動后續機構的動作，由此導致整個包含諧波減速器的傳動機構無法動作，此時也即判定諧波減速器是失效的。因此，諧波齒輪傳動效率的性能裕量可描述為：

m =η- ηth

（8）

當性能裕量m>0時，傳動效率不會達到失效閾值，諧波減速器能夠驅動后續機構的動作，可以完成規定的功能;當m<時，傳動效率已經超過失效閾值，諧波減速器無法驅動后續機構的動作，認為其已經失效;當m=0時，傳動效率等于失效閾值，諧波減速器處于正常工作與失效的臨近狀態。

1.3 不確定性分析與量化

可靠性科學原理指出產品的性能裕量是不確定的（不確定原理）[19]，其中，性能裕量的不確定性包含性能參數的不確定性及其閾值的不確定性。性能參數的不確定性主要來源于產品內在屬性（如尺寸、材料等）和交互的外界條件（如工作應力、環境應力等）的不確定性;閾值的不確定性主要來源于對產品功能邊界的不清晰的認知。

為了量化不確定性，一般而言，不確定性的種類可以分為兩類，一類是隨機不確定性，另一類是認知不確定性[20]。隨機不確定性表征為現實世界固有存在的、無法被消除的隨機性特征。認知不確定性表征由于人的知識不完備導致的非確定性。通過各種科學實踐，能夠提高對客觀世界的認知，進而降低認知不確定性。在本文中，僅考慮隨機不確定性的存在，并選用概率論對隨機不確定性進行量化。

考慮到諧波減速器生產和制造過程中存在的不確定性以及工作應力和環境條件中的不確定性，實際測量得到的諧波齒輪傳動效率數據會呈現波動性的特點。為此，在諧波齒輪傳動效率模型（6）中引入一個不確定項ε，并假設ε是一個隨機變量，服從均值為0，標準差為σ的正態分布，即ε-～N（0，σ2）。那么，考慮不確定性的諧波齒輪傳動效率模型為：

諧波齒輪傳動效率的失效閾值需要基于具體的諧波齒輪的功能和性能分析，并通過開展實驗進行確定。為了使得諧波減速器能夠順利地傳遞運動，當諧波減速器的輸入力矩一定時，由公式（1）可知，其傳動效率決定著其輸出力矩，這個輸出力矩又作為后一機構的輸入力矩進行運動的傳遞。當諧波減速器的輸出力矩小于后一機構的啟動力矩時，便無法傳遞運動，整個傳動機構也就失效了;或者當諧波減速器的輸出力矩小于某規定力矩時，也可認為諧波減速器不能滿足規定的功能。通過實驗的方式可以辨識諧波減速器在上述兩種情況下的輸入力矩和輸出力矩，進而獲得諧波齒輪傳動效率的失效閾值。由于產品不可避免地存在不確定性，同一種機構的啟動力矩也并非是一個固定數值[21-22]。另一方面，諧波減速器的輸入力矩取決于前一機構的輸出力矩，同樣有不確定性。因此，諧波齒輪傳動效率的閾值也存在不確定性。假設其閾值ηth是一個隨機變量，服從均值為ηth，標準差為σth的正態分布，即ηth～N（ηth，σth）。

將考慮不確定性的諧波齒輪傳動效率77及其閾值ηth代人公式（8），可得：

m=η-ηth

（II）

由公式（11）可知，諧波齒輪傳動效率的性能裕量m也是一個隨機變量，其概率密度函數為

1.4 確信可靠性建模

基于可靠性科學原理提出的確信可靠性理論[10]指出，產品可靠度可以采用概率論、不確定理論[23]和機會理論[24]來度量。其中，概率論用來描述隨機不確定性;不確定理論用來描述認知不確定性;而機會理論用來描述隨機和認知的混合不確定性。對于受到隨機和/或認知的混合不確定性影響的系統，稱之為不確定隨機系統，其性能參數為不確定隨機變量。

定義（確信可靠度）[19]設系統的性能裕量m為不確定隨機變量，則確信可靠度是系統的性能裕量大于0的機會，即：

式中 Ch{.}為機會測度。

如果系統主要受到隨機不確定性的影響，那么系統會退化為一個隨機系統，系統的性能裕量m隨之退化為一個隨機變量。此時，確信可靠度在數學上退化為了概率測度下的可靠度，即經典的概率可靠度，表示的是性能裕量大于0的頻率。令RIP）表示概率論下的確信可靠度，則：

本研究僅考慮隨機不確定性對諧波齒輪傳動效率的影響，因此采用概率論對諧波齒輪傳動效率的確信可靠度進行度量，將公式（11）代人公式（14）可得：

2 統計分析

假設針對某型號諧波減速器開展了傳動性能試驗，令ηijk為負載水平M，，轉速水平wj和溫度應力水平Tk下的傳動效率試驗數據，i=1，2，…，l;j=1，2，…，m;k=1，2，…，n，其中l為負載水平數，m為轉速水平數，咒為溫度應力水平數。在構建的考慮不確定性的諧波齒輪傳動效率模型（9）中，未知參數集為θ={ a1，a2，a3，a4，σ}。

本文采用極大似然方法對未知參數進行估計，可以得到基于上述諧波傳動效率測試數據的似然函數為：

3 案例研究

3.1 諧波齒輪傳動效率測試數據

某公司針對XB40-100的諧波減速器（傳動比為100，潤滑方式采用空間潤滑油脂）開展多應力類型（負載扭矩、轉速和溫度應力）多應力水平的傳動效率性能試驗，試驗設置如表1所示，試驗測得的諧波減速器傳動效率數據如圖4所示。

3.2 參數估計

基于第2節的統計分析方法，可以得到考慮不確定性的諧波齒輪傳動效率模型（9）中未知參數的估計結果，如表2所示。

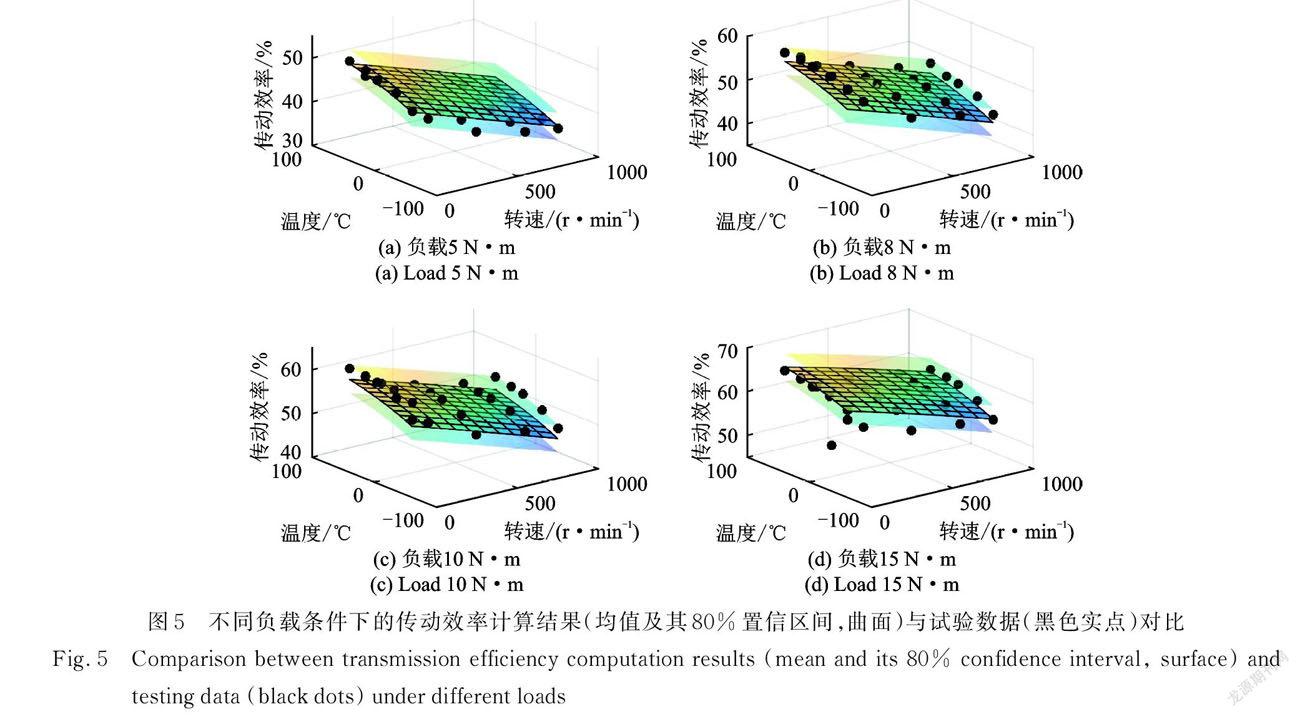
將參數估計結果代人到諧波齒輪傳動效率模型（9）中，可得在負載扭矩為5，8，10和15N.m的條件下諧波齒輪傳動效率及其80%置信區間，結果如圖5所示。

由圖5可以看出，各負載條件下的諧波齒輪傳動效率試驗數據幾乎都在所提的傳動效率計算結果的80%置信區間內，且都在其均值曲面附近，均勻地分散在均值曲面兩側。結果表明，所提的諧波齒輪傳動效率模型可以有效地將試驗數據與理論模型結合，以彌補潤滑方式、負載、轉速和溫度對諧波齒輪傳動效率影響機理不明的問題，進而準確地計算在諧波減速器在給定潤滑方式、負載、轉速和溫度條件下的傳動效率。

3.3 確信可靠性評估與分析

假設XB40-100諧波減速器的實際負載扭矩為5～15 N-m，轉速為100～1000 r/min，環境溫度為一35～65℃，以及諧波齒輪傳動效率失效閾值為N（40%，（5%）2）。根據公式（11），選定負載扭矩為5，8，10和15 N-m，計算不同轉速和溫度條件下諧波齒輪傳動效率裕量及其80%置信區間，如圖6所示。根據圖6，可以得到以下兩點結論：

1）諧波齒輪傳動效率裕量隨著轉速的降低而升高，隨著溫度的升高而升高，這與1.2節轉速和溫度對諧波齒輪傳動效率影響的分析結果一致，即降低轉速和升高溫度有助于減小摩擦損耗，進而提高了諧波齒輪傳動效率，增加了傳動效率裕量，提高了可靠性。

2）隨著負載扭矩的增加，諧波齒輪傳動效率裕量升高，這與1.2節負載扭矩對摩擦因數的分析結果相反。原因在于，負載扭矩對諧波齒輪傳動效率的影響是雙面的：一方面，負載扭矩直接影響諧波減速器的輸出功率，根據公式（3）可知，負載扭矩越大，傳動效率越高;另一方面，根據1.2節負載扭矩對摩擦因數的影響分析，增加負載扭矩會增大摩擦損耗，進一步會降低傳動效率，該分析結果與表2中的參數估計結果一致，即a2=0.075>0，摩擦因數與負載扭矩正相關。但是從諧波齒輪整體的傳動角度考慮，負載扭矩提高傳動效率的正向影響遠大于摩擦因數對傳動效率的抑制作用。故負載扭矩對傳動效率的影響最終體現為：增加負載扭矩，諧波齒輪傳動效率升高，其傳動效率裕量也升高。

根據公式（15），可以計算得到其對應的確信可靠度，如圖7所示。上述從傳動效率裕量角度的分析結果與圖7中的確信可靠度結果一致。確信可靠度隨著負載扭矩的升高，轉速的降低和溫度的升高而升高。因此，在諧波減速器的實際使用過程中，根據諧波減速器的實際使用情況，可以適當提高諧波減速器的負載扭矩、降低其轉速或者提高環境溫度，這有助于提高諧波齒輪傳動效率可靠性。

4 結 論

本文基于可靠性科學原理和確信可靠性理論，對諧波齒輪傳動效率的確信可靠性建模與分析開展研究。首先，本文考慮了諧波減速器輸入功率的能量消耗，包括輸出功率、嚙合摩擦損耗、由于嚙合力在諧波軸承中引起的摩擦損耗和薄壁零件初變形所需徑向力在諧波軸承中所引起的摩擦損耗等，以及外在影響因素對傳動效率的影響，包括潤滑方式、負載、轉速和環境溫度等，通過在諧波齒輪傳動效率理論計算模型中引入代理模型的方式，構建了考慮多種外在影響因素的諧波齒輪傳動效率模型。進一步考慮了傳動效率與其閾值之間的距離，構建了諧波齒輪傳動效率裕量模型。然后，對裕量模型中的多源不確定性進行分析和量化，給出了諧波齒輪傳動效率的確信可靠性模型。最后，基于極大似然估計方法，對模型中的未知參數進行標定。

通過一個XB40-100諧波減速器的案例驗證了所提方法的實用性和有效性。結果表明，所提的諧波齒輪傳動效率模型可以有效地將試驗數據與理論模型結合，進而準確地計算諧波減速器在給定負載、轉速和溫度條件下的傳動效率。通過諧波減速器傳動效率的確信可靠性分析，發現適當提高諧波減速器的負載扭矩、降低其轉速或者提高環境溫度有助于提高諧波減速器傳動效率裕量及其確信可靠性。

可靠性科學原理指出，產品會沿著退化時矢發生不可逆的退化（退化永恒原理）[19]，但是本文開展的諧波齒輪傳動效率確信可靠性分析并沒有考慮退化的影響。實際上，諧波齒輪傳動效率的退化非常緩慢，但是在長期工作下，在諧波減速器的長期使用過程中，不可避免地會發生磨損，潤滑環境會變得惡劣，這些都會增大諧波減速器的摩擦耗損，進而降低諧波齒輪傳動效率裕量及其可靠度，因此，退化對傳動效率可靠性的影響不可忽視。此外，在諧波減速器的退化過程中，仍然存在著多種多樣的不確定性，如負載、轉速和環境溫度的不確定性等，這些都會影響諧波減速器的磨損過程，進而增大可靠性建模與分析的難度。因此，在未來諧波齒輪傳動效率可靠性的研究中，需要科學合理地構建諧波齒輪傳動效率的退化模型，考慮多源不確定性，進行可靠性分析與研究。

參考文獻：

[1]

Musser C W. The harmonic drive： breakthrough in me-chanical drive design [Jl. Machine Design， 1960， 14：89-93.

[2] 11 Xin-zi， SONG Chao-sheng， YANG Yong， et al.Optimal design of wave generator profile for harmonicgear drive using support function[J]. Mechanism andMachine Theory， 2020， 152： 103941.

[3] LIAO Hong-bo， FAN Shi-xun， FAN Da-peng. Fric-tion compensation of harmonic gear based on location re-lationship[J].Proceedings of the Institution of Mechani-cal Engineers， Part I：Joumal of Systems and ControlEngineering， 2016， 230（8）：695-705.

[4]施祖康，肖詩林，遲云.諧波齒輪傳動的機械傳動效率[J].南京理工大學學報（自然科學版），1985（4）：107 117.

SHI Zu-kang， XIAO Shi-Iin， CHI Yun. The mechani-cal efficiency of the harmonic drive [J]. Journal of Nan-jing University of Science and Technology， 1985（4）：107-117.

[5]陳樺，孫波，龐靜.諧波齒輪傳動的效率分析[J].機械科學與技術，1995（3）：49-53.

CHEN Hua， SUN Bo， Pang Jing. Effciency analysisfor harmonic drives[J]. Mechanical Science and Tech-nology for Aerospace Engineering ，1995（3）：49-53.

[6]Ianici Sava， Ianici Draghita. Constructive design and dy-namic testing of the double harmonic gear transmission[J]. Analele Universitatii Eftimie Murgu Resita， 2015，22（1）：231-238.

[7]楊連花.諧波行星復合減速裝置的設計研究及仿真分析[D].西安：長安大學，2017.

YANG Lian-hua. Design research and simulation analy-sis on composite speed reducer of harmonic and plane-tary[D]. Xi' an： Chang' an University， 2017.

[8]李德舉.基于ABAous的諧波傳動效率計算方法研究[D].大連：大連理工大學，2013.

LI De-ju. Research on calculation methods of the effi-ciency of harmonic drive based on ABAous [D]. Da-lian： Dalian University of Technology， 2013.

[9]肖京.不同齒形諧波齒輪傳動效率研究及嚙合仿真[D].秦皇島：燕山大學，2016.

XIAO Jing. Research on transmission efficiency andmeshing simulation of different tooth harmonic gear[D]. Qinhuangdao： Yanshan University， 2016.

[10]夏田，楊世勇，何乃如，等.工業機器人用諧波減速器傳動性能正交試驗分析[J].科學技術與工程，2017，19：138-141.

XIA Tian， YANG Shi-yong， HE Nai-ru， et al.Orthog-onal experiment analysis on transmission performance ofharmonic drive for industrial robots [J]. Science Tech-nology and Engineering， 2017， 19： 138-141.

[11]李波，李瑞祥.超載條件下空間潤滑諧波減速器傳動性能及摩擦磨損性能研究[J].摩擦學學報，2011， 31（3）：216-220.

LI Bo， LI Rui-xiang. Transmission behaviors and tribo-logical properties of the solid and grease lubricated har-monic drivers at overload condition[J]. Tribology，2011， 31（3）：216-220.

[12]李波.基于交互正交試驗的空間用諧波減速器傳動性能影響因素研究[J].航空學報，2012， 33（2）：375-380.

LI Bo. Research of factors affecting transmission perfor-mance of harmonic drive in spacecraft based on interac-tive orthogonal experiment[J].Acta Aeronautica et As-tronautica Sinica， 2012， 33（2）：375-380.

[13]ZHOU Guang-wu， ZHANG Zhen-hua， ZHUANGHua. Experimental study on transmission performanceof harmonic drive under multifactor interaction[J].Me-chanics&Industry， 2019， 20（6）：614.

[14]李俊陽，王家序，范凱杰，等.諧波減速器黏著磨損失效加速壽命模型研究[J].摩擦學學報，2016. 36（3）：297-303.LI Jun-yang， WANG Jia-xu， FAN Kai-jie， et al.Ac-celerated life model for harmonic drive under adhesivewear[J].Tribology， 2016， 36（3）：297-303.

[15]LI Jun-yang， WANG Jia-xu. ZHOU Guang-wu， et al.Accelerated life testing of harmonic driver in space lubri-cation[Jl. Proceedings of the Institution of MechanicalEngineers， Part J：Journal of Engineering Tribology，2015， 229（12）： 1491-1502.

[16]官浩.空間諧波減速器性能退化與壽命分析研究[D].重慶：重慶大學，2014.

GUAN Hao. Research on performance degradation andlife analysis of space harmonic driver[Dl. Chongqing：Chongqing University， 2014.

[17]王洪星.諧波齒輪傳動效率的計算方法[J].北京航空學院學報，1982（3）：111-120.

WANG Hong-xing. Efficiency equations for differenttypes of harmonic drives[J].Journal of Beijing Instituteof Aeronautics and Astronautics， 1982（3）：111-120.

[18]梁作斌，杜佳佳，郭梅.齒輪風阻損失仿真及其實際應用[J].航空動力學報，2017， 32（6）：1419-1424.

LIANG Zuo-bin. Du Jia-jia， Guo Mei. Simulation ofgear windage losses and its application [Jl. Journal ofAerospace Power， 2017， 32（6）：1419-1424.

[19]康銳.確信可靠性理論與方法[M].北京：國防工業出版社，2020.

KANG Rui. Belief Reliability Theory and Methodology[M]. Beijing： National Defense Industry Press， 2020.

[20]ZHANG Qing-yuan， KANG Rui， WEN Mei-Iin. Beliefreliability for uncertain random systems [Jl. IEEETransactions on Fuzzy Systems， 2018， 26 （6） ：3605-3614.

[21]王建輝，李良，董紅衛，等.RV減速器性能試驗研究[J].機械工程師，2018， 326（8）：127-129.

WANG Jian-hui. LI Liang， DONG Hong-wei， et al.Experimental study on performance of RV reducer [J].Mechanical Engineering， 2018， 326（8）：127-129.

[22]柏德恩，全齊全，李賀，等.伺服加載的諧波減速器啟動力矩測試系統[J].吉林大學學報（工學版），2017（6）：1804-1810.

BAI De-en， QUAN Qi-quan， LI He， et al.Startingtorque test system for harmonic drive based on servoloading[J].Journal of Jilin University（ Engineering andTechnology Edition）， 2017（6）：1804-1810.

[23]LIU Bao-ding. Uncertainty Theory[M].Berlin： Spring-er， 2010.

[24]Liu Yu-han. Uncertain random variables：a mixture ofuncertainty and randomness[J]. Soft Computing，2013， 17（4）：625-634.