基于深度學習及傳統機器學習模型估算山東省參考作物蒸散量

任傳棟，王志真，馬 釗，張 敏

（山東省水利勘測設計院，濟南250013）

0 引 言

蒸散（Evapotranspiration，ET）由植株蒸騰與株間蒸發2部分組成，其值的準確估算對灌溉需水量確定及農田生態系統評價意義重大[1,2]。參考作物蒸散量（Reference crop evapotranspiration，ET0）的估算精度在一定程度上決定了ET的估算精度，它是作物系數法估算區域ET的重要參數之一[3]。FAO-56 分冊規定的Penman-Monteith（PM）模型綜合考慮了能量平衡和空氣動力學的相關理論，是估算ET0的標準模型[4,5]。PM 模型計算時涉及到了多個氣象參數，例如最高溫度、最低溫度、相對濕度、風速等，這使得該模型的廣泛應用性受到了一定的限制[6]。因此，研究區域ET0估算的簡化模型，在保證估算精度的前提下使用較少的氣象參數，這對區域灌溉決策的制定具有十分重要的意義。

為更好地估算區域ET0，研究學者采用了多種ET0簡化計算的經驗模型，例如溫度模型、輻射模型、質量傳輸模型、蒸發皿模型等，在這些模型中，溫度模型、輻射模型和質量傳輸模型的應用較廣泛[7,8]。Almorox 等[9]研究比較了11 種溫度模型的計算精度，指出了Hargreaves（HS）模型精度最高；楊永剛等[10]在中國三大灌區比較了8 種溫度模型的精度，指出HS 模型在河套灌區的精度最高；Feng 等[11]比較了Priestley-Taylor（PT）、Makkink（MK）和Ritchie （RC）3 種輻射模型的精度，指出PT 模型在3 種輻射模型中的精度最高；吳宗俊等[12]利用差分進化算法對MK 模型進行了改進，并在四川盆地驗證了該模型精度，指出改進后的MK 模型R2可達0.87，精度優于其余模型；褚榮浩等[13]比較了質量傳輸模型與其余10 種模型的精度，驗證了質量傳輸模型的適用性。盡管經驗模型已表現出了出色的性能，但它們的性能在不同地區之間存在很大差異[14]。

近年來，深度學習模型已在不同領域證明了其精度，深度學習模型應用最廣泛的包括深度神經網絡（DNN）、時間卷積神經網絡（TCN）和長短期記憶神經網絡（LSTM）3 種[14]。Zhang 等[15]基于LSTM 模型預測了中國西北干旱地區河套灌區五個分區的地下水位深度動態變化；Wang 等[16]在地下水流動中驗證了DNN 模型的精度；邢立文等[17]在華北地區驗證了LSTM模型的精度。

深度學習模型已在不同領域取得了較高的精度，但在ET0估算中的應用仍然較少。為證明深度學習模型在ET0估算中的適用性，本文以山東省為研究區域，選擇DNN、TCN 和LSTM 3 種深度學習模型估算區域ET0，并將計算結果與傳統機器學習模型和經驗模型進行對比，在有限氣象資料輸入的條件下，找尋最優模型。

1 研究區域概況與研究方法

1.1 研究區域概況及數據來源

山東省位于我國中東部沿海地區，屬暖溫帶季風氣候區，降水時空分布不均，旱澇災害頻發對當地經濟造成了嚴重影響。由于區域地形變化較大，導致區域水循環差異明顯，因此，研究山東省的ET0最優估算模型，對當地防旱防澇政策的制定具有十分重要的意義。本文選擇山東省惠民、青島、濟南等10 個站點1980-2018年的逐日氣象數據，氣象數據來自國家氣象數據中心，質量控制良好，主要包括日最高氣溫（Tmax）、最低氣溫（Tmin）、日照時數（n）、相對濕度（RH）和10 m處風速（U10），站點分布情況可見圖1。

1.2 研究方法

1.2.1 Penman-Monteith模型

Penman-Monteith 模型（PM 模型）可作為ET0計算的標準模型[4]，具體公式如下：

式中：Rn為作物表面的凈輻射，MJ/（m2·d）；T為2 m 高處的日均氣溫，℃；G為土壤熱量通量密度，MJ/（m2·d）；U2為2 m 高處風速，m/s；采用FAO 推薦方法[4]由10 m 風速換算得出；es為飽和水汽壓差，kPa；ea為實際水汽壓差，kPa；Δ為蒸汽壓曲線的斜率，kPa/℃；γ為干濕計常數，kPa/℃。

1.2.2 深度學習模型

（1）長短期記憶神經網絡。長短期記憶神經網絡模型（LSTM）可有效記憶數據歷史規律，避免了傳統神經網絡模型數據參數的隨機性。該模型由輸入閥門、遺忘閥門、更新閥門和輸出閥門4部分組成。通過閥門的開啟與關閉，判定模型計算結果能否滿足精度要求，模型具有步驟可見文獻[17]。

①遺忘閥門。LSTM 模型的遺忘閥門Fi基于sig 激活函數，讀取舊元素的輸出值Yi-1和新元素的輸入值Xi，并基于模型權重判定是否應該保留新元素，原理公式如下：

式中：Fi為模型遺忘閥門；W為權重；b為偏執矢量；σ為sig激活函數。

②輸入閥門。輸入閥門Ii可判斷輸出值能否達到預期，輸入閥門不但可以決定當前元素的輸出值Yi，同時可基于tanh激活函數創建新的候選變量，從中選出最優值，原理公式如下：

式中：Ii為模型輸入閥門；tanh 為模型激活函數；Ui為候選變量，其余參數含義同上。

③更新閥門。更新閥門Zi將輸入閥門與遺忘閥門相乘，來判斷當前元素的狀態是否由Si-1更新到Si，原理公式如下：

④輸出閥門。輸出閥門Oi計算當前元素的輸出值Yi，基于sig和tanh 2個激活函數最終確定模型輸出值，原理公式如下：

式中：Yi為模型輸出值；Oi為輸出閥門，其余參數含義同上。

（2）時間卷積神經網絡。時間卷積神經網絡（TCN）是Bai 等[18]在傳統卷積神經網絡（CNN）的基礎上發展起來的。與CNN 模型相比，TCN 模型具有因果卷積和擴展卷積兩個顯著的特征，使得TCN 模型在解決序列問題上明顯優于一些傳統神經網絡模型，在TCN 模型計算中，時間t的輸出包含了之前的信息，這意味著TCN 模型可以“記憶”更長的過去信息。當考慮隨意卷積和擴張卷積時，時間t的輸出可用下式表示，模型具體步驟可見文獻[18]。

式中：F(t)為時間t的輸出函數；fi為濾波函數；xi為輸入項；d為修正系數；K為輸入項的個數。

（3）深度神經網絡。深度神經網絡（DNN）是一種新型的人工神經網絡模型，其權值和偏差通過BP 神經網絡模型進行訓練。與傳統的BP 神經網絡模型相比，DNN 模型具有更多的隱藏層，使其具有強大的能力來處理許多行業的回歸和分類任務，DNN 模型包括兩個主要過程，分別為前饋過程和誤差反向傳播過程，具體步驟可見文獻[6]。

1.2.3 傳統機器學習模型

為進一步證明深度學習模型的精度，本文選擇了3種傳統機器學習模型，分別為極限學習機模型（ELM）、廣義回歸神經網絡模型（GRNN）和隨機森林模型（RF），在相同氣象參數輸入的條件下，比較3 種傳統機器學習模型與3 種深度學習模型的精度，3種傳統機器學習模型步驟可見文獻[2]。

1.2.4 經驗模型

為進一步驗證深度學習模型在不同氣象參數輸入下的精度，本文選擇了6 種經驗模型進行精度對比，包括2 種溫度模型、2 種輻射模型和2 種質量傳輸模型，具體公式和參數含義可見表1。

表1 經驗模型公式及參數

1.3 模型驗證與精度對比

采用3 種氣象參數輸入組合訓練模型，分別對應基于輻射、溫度的和質量傳輸的經驗模型。基于1980-2010年的氣象數據訓練模型，2011-2018年的數據預測模型，不同氣象組合方式可見表2。

表2 不同模型參數組合輸入方式

選擇均方根誤差（RMSE）、決定系數（R2）、平均絕對誤差（MAE）和效率系數（Ens）組成模型精度指標評價體系，公式如下：

式中：Xi和Yi分別為模型模擬值及實測值；-X和-Y分別為Xi和Yi的平均值。

GPI指數可整合4個指標的綜合評價結果[24]，公式如下：

式中：αj為常數；MAE和RMSE取1，Ens和R2取-1；gj為不同指標的縮放值的中位數；yij為不同指標的尺度值。

2 結果與分析

2.1 不同溫度模型模擬精度對比

表3 反映了不同溫度模型與PM 模型計算結果擬合方程斜率對比。表4 顯示，TCN 模型擬合方程斜率最接近標準值“1”，在不同站點均達到了0.80 以上。3 種深度學習模型的擬合效果均優于其余模型，擬合效果由高到低依次為TCN 模型＞LSTM模型＞DNN模型，3種模型擬合方程斜率均在0.749以上。相同氣象參數輸入條件下，機器學習模型精度普遍優于經驗模型，HS模型、DA模型與PM模型計算結果的擬合性較差。

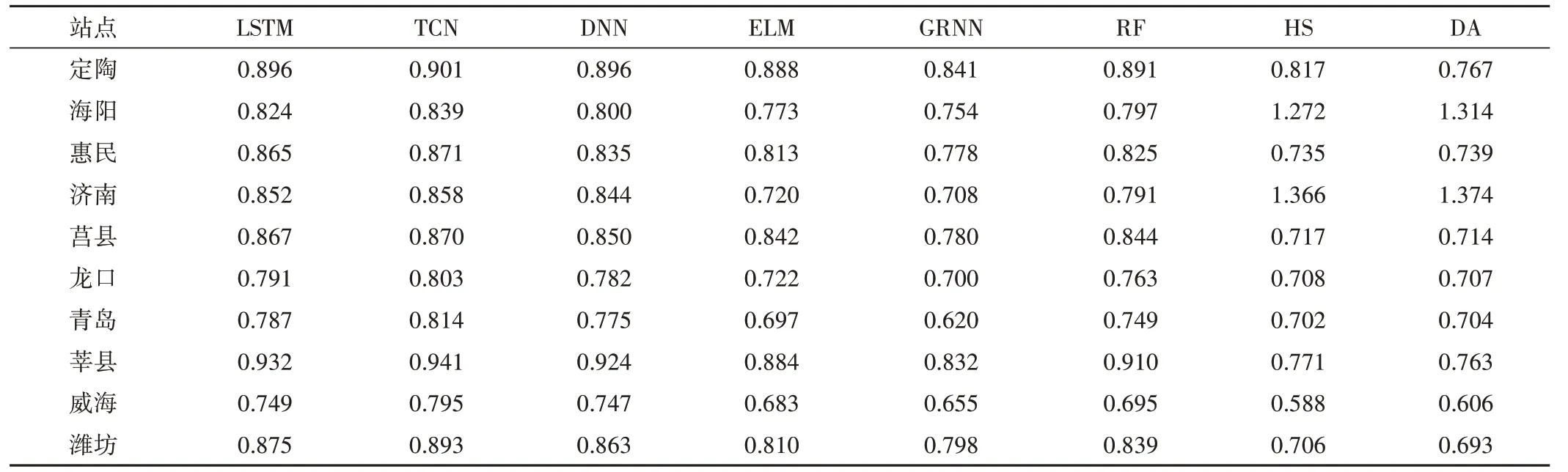
表3 不同溫度模型ET0日值與PM模型標準值擬合方程斜率對比

圖2 為不同溫度模型的計算精度對比。由圖2 可以看出，不同溫度模型計算精度存在差異，其中TCN 模型在不同模型中的精度最高，其RMSE、R2、Ens、MAE的中位數分別為0.523 mm/d、0.874、0.870和0.388 mm/d。3種深度學習模型精度普遍優于其余模型，3 種深度學習模型的RMSE、R2、Ens和MAE的中位數分別為0.523～0.674 mm/d、0.788～0.874、0.784～0.870 和0.388～0.502 mm/d。3 種傳統機器學習模型精度優于2種經驗模型，其中RF 模型和ELM 模型的精度較高，GRNN 模型的精度較低。HS 模型和DA 模型的精度較低，其RMSE、R2、Ens和MAE的中位數分別為0.964 和1.117 mm/d、0.741 和0.736、0.560 和0.507、0.761 和0.897 mm/d。總體而言，與其余模型相比，深度學習模型表現出更好的計算精度，其在不同站點的精度均較高，計算結果的隨機性較低。

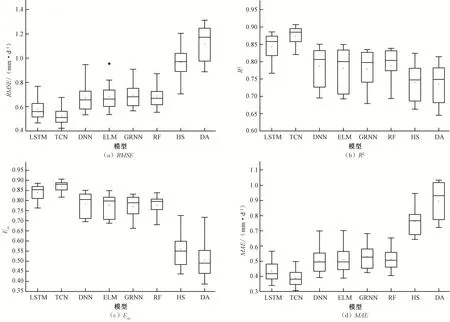
圖2 不同溫度模型模擬ET0精度對比

2.2 不同輻射模型模擬精度對比

表4 為不同輻射模型與PM 模型計算標準值擬合方程斜率對比。表4顯示，輻射模型的擬合效果明顯優于溫度模型，同時TCN 模型效果最優，其在不同站點的擬合方程斜率在0.904～1.021之間。3種深度學習模型的擬合效果均優于其余模型，擬合效果表現為TCN模型＞LSTM模型＞DNN模型，擬合方程斜率均在0.85 以上。相同氣象參數輸入條件下，機器學習模型精度普遍優于經驗模型，HS 模型、DA 模型與PM 模型計算結果的擬合性較差，擬合方程斜率距標準值“1”的偏差較大，表明經驗模型在計算ET0時具有較大的隨機性。

表4 不同輻射模型ET0日值與PM模型標準值擬合方程斜率對比

圖3 為不同輻射模型的計算精度對比。由圖3 可以看出，不同輻射模型計算精度存在差異，但精度總體優于溫度模型，其中TCN 模型在不同模型中的精度最高，其RMSE、R2、Ens、MAE的中位數分別為0.319 mm/d、0.952、0.950和0.231 mm/d。3 種深度學習模型精度普遍優于其余模型，RMSE、R2、Ens和MAE的中位數分別為0.319～0.409 mm/d、0.920～0.952、0.921～0.950 和0.231～0.307 mm/d，其中，TCN 模型精度最高，LSTM模型精度次之。3種傳統機器學習模型精度優于2種經驗模型，其中ELM 模型和RF 模型的精度較高，RMSE、R2、Ens和MAE的中位數分別為0.416 和0.444 mm/d、0.915 和0.907、0.914 和0.904、0.330 和0.328 mm/d。HS 模型和DA 模型的精度較低，其RMSE、R2、Ens和MAE的中位數分別為0.726 和0.769 mm/d、0.806和0.838、0.738和0.712、0.555和0.601 mm/d。

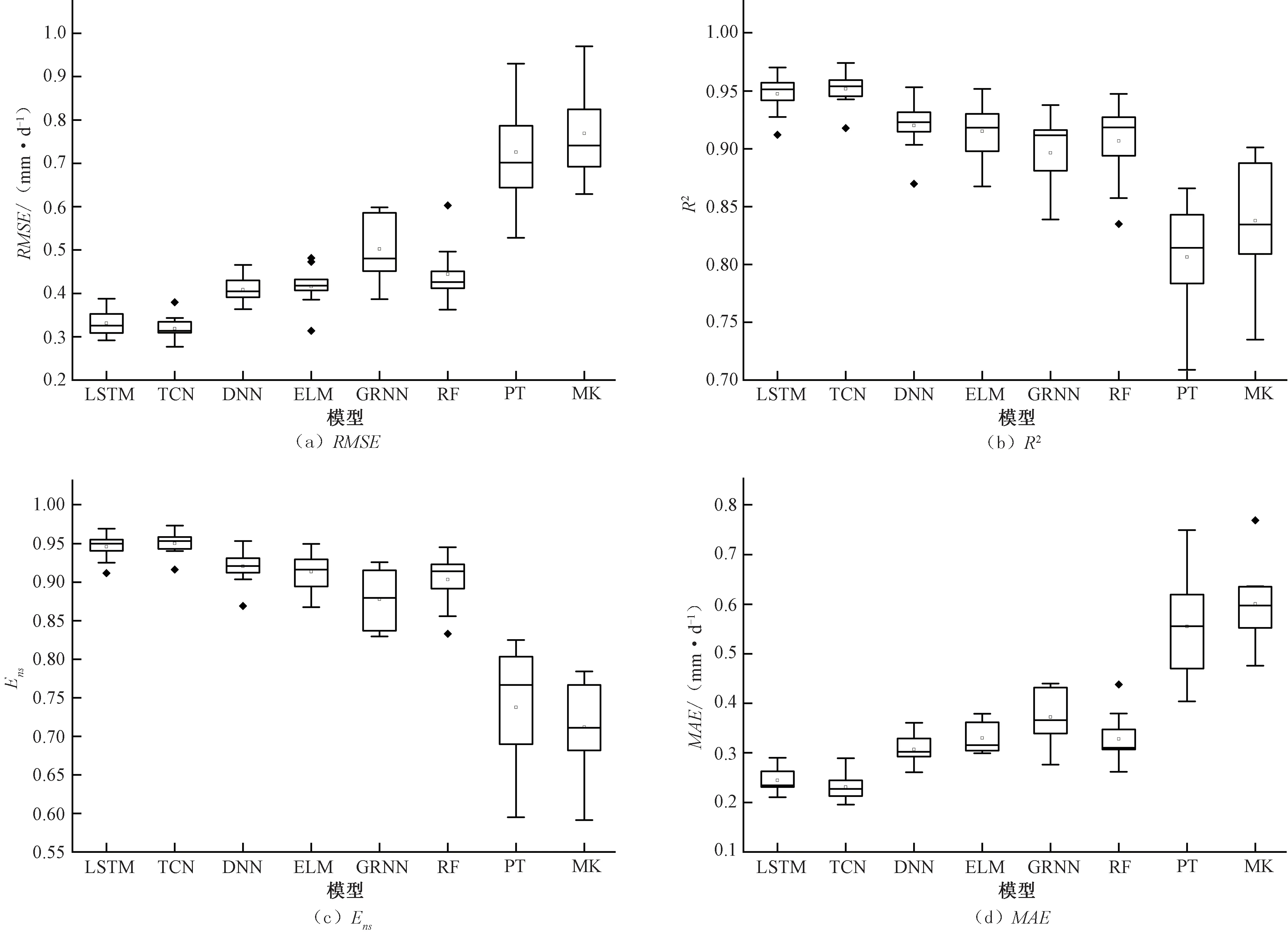
圖3 不同輻射模型模擬ET0精度對比

2.3 不同質量傳輸模型模擬精度對比

表5 為不同質量傳輸模型與PM 模型計算標準值擬合方程斜率對比。表5顯示，質量傳輸模型的擬合效果介于溫度模型與輻射模型之間，同樣表現為TCN 模型擬合精度最高，其在不同站點的擬合方程斜率均在0.886～0.979 之間。3 種深度學習模型的擬合效果均優于其余模型，擬合方程斜率均在0.85以上。HS 模型、DA 模型與PM 模型計算結果的擬合性較差，擬合方程斜率與標準值“1”的偏差在0.163～0.367之間。

表5 不同質量傳輸模型ET0日值與PM模型標準值擬合方程斜率對比

圖4 為不同質量傳輸模型的計算精度對比。由圖4 可以看出，不同質量傳輸模型的精度明顯優于溫度模型，但略低于輻射模型。TCN 模型在不同模型中的精度最高，RMSE、R2、Ens、MAE的中位數分別為0.358 mm/d、0.943、0.939 和0.263 mm/d。相同輸入參數下的機器學習模型精度普遍優于經驗模型，其中3種深度學習模型的精度較高。HS模型和DA 模型的精度較低，其RMSE、R2、Ens和MAE的中位數分別為0.851 和0.870 mm/d、0.706 和0.740、0.683 和0.685、0.731 和0.714 mm/d。

圖4 不同質量傳輸模型模擬ET0精度對比

綜上所述，深度學習模型精度普遍優于其余模型，其中，TCN模型在不同氣象參數輸入下均表現出了較高的精度。

2.4 不同模型GPI對比

為綜合判定不同輸入參數組合下不同模型的計算精度，本文綜合比較了24 種模型的GPI，結果見圖5。由圖5 可以看出，在不同模型中，輻射模型精度最高，質量傳輸模型精度次之，溫度模型精度較低。TCN2 模型在所有模型中精度最高，GPI 中位數為1.036，LSTM2 模型精度次之，GPI 為0.975。溫度模型和質量傳輸模型中，均表現為TCN 模型精度最高，GPI 分別為-0.006 和0.873。相同參數輸入下的經驗模型精度較低，其中HS和DA模型GPI僅為-2.365和-2.877。

圖5 不同參數輸入組合下不同模型GPI對比

3 討 論

已有研究表明，輸入氣象參數組合的不同對模型預測ET0的精度起著主要作用[25]。不同區域研究均表明，輻射數據是保障ET0較高估算精度的關鍵參數[26]。Feng 等[27]指出基于溫度和輻射參數作為機器學習模型的輸入組合，可保證模型較高的精度。3 種類型模型表現出的精度由高到低依次為輻射模型、質量傳輸模型、溫度模型，表明輻射是影響山東省ET0變化的關鍵因素。董旭光等[28]指出近50年，日照時數和風速是影響山東省ET0變化的主要因素，這與本文結論基本一致。當僅有溫度數據輸入時，機器學習模型精度高于經驗模型，可滿足ET0估算的精度要求。需要指出的是，本文中不僅使用了氣溫數據（Tmin和Tmax），而且將Ra數據作為了溫度組合重要的輸入參數，Ra數據可從年日和緯度得到，可近似作為全球太陽輻射，引入Ra作為訓練數據的輸入，提高了基于溫度模型的準確性。在中國，溫度資料的獲取是最為方便的，因此基于溫度的機器學習模型可實現實時快捷預報ET0，從而改善灌溉和水資源管理[29]。對于質量傳輸模型，與溫度模型相比，引入相對濕度和風速等氣候數據，可提高模型精度，但其精度低于輻射模型，因此，對于質量傳輸模型的應用性有待進一步討論。

傳統機器學習模型參數確定的隨機性導致了模型誤差較大，影響了最終模型模擬的結果。本文比較了3種深度學習模型與其余傳統機器學習模型的精度，指出了3種深度學習模型的精度普遍較高，因此，深度學習模型可以有效避免參數的隨機性選取，從而產生隨機初始化權值和隱藏偏差，最終避免了非最優解，提高了模型精度[30]。深度學習模型通過對模型訓練數據的學習，從而自行進行數據特征選擇，能夠更好地揭示數據的客觀規律，提高模型精度。TCN 模型的廣泛應用可為農業、水利、氣象部門活動提供數據支撐，保證國家糧食生產及水資源的合理利用。

4 結 論

本文以LSTM 模型、TCN 模型和DNN 模型3 種深度學習模型為基礎，與ELM、GRNN、RF3 種傳統機器學習模型和HS、DA等6種經驗模型對比，找到山東省ET0估算的最優模型，得出以下結論：

（1）3 種深度學習模型精度普遍優于其余模型，TCN 模型具有最高的精度，在不同站點擬合方程斜率最接近標準值“1”，RMSE、R2、Ens、MAE的中位數在0.318～0.523 mm/d、0.874～0.952、0.870～0.950、0.231～0.388 mm/d，TCN 模型在所有模型中GPI數值均最高；

（2）基于輻射的模型優于基于溫度和質量傳輸的模型，TCN2 模型在所有模型中精度最高，其RMSE、R2、Ens、MAE的中位數分別為0.318 mm/d、0.952、0.950、0.231 mm/d，同時GPI達到了1.036，在所有模型中排名第1位。

綜上所述，深度學習模型可作為區域ET0估算的推薦模型使用，其中以TCN模型精度最高。