懸掛式有軌制導車輛車體多目標參數優化設計

□ 陳 思 □ 李成群

華北理工大學 機械工程學院 河北唐山 063210

1 優化設計背景

當前,物流倉儲技術不斷發展。懸掛式有軌制導車輛作為新型搬運設備,不僅能夠滿足高效物流搬運作業的需要,而且對環境的適應性更強,改變了傳統人工作業模式,提高了倉儲空間的利用率[1-2]。

懸掛式有軌制導車輛車體的質量和力學特性對搬運系統整體性能和功能有至關重要的影響。在承受既定載荷和給定約束的前提下,對懸掛式有軌制導車輛進行合理的結構布局和尺寸參數優化,通過計算機分析,得到最優的結構方案[3]。洪求才等[4]在對車架進行優化時,既保證了車架的動態特性和強度要求,又達到了輕量化的設計目的。Zhang Ran等[5]在對電動車進行優化時,結合靈敏度分析法提高了優化效率。

筆者對懸掛式有軌制導車輛車體進行多目標參數優化設計,選擇滿載工況進行分析,結合靈敏度分析、響應面分析、模態分析,在滿足輕量化設計原則的前提下,優化車體框架尺寸和結構分布,提高懸掛式有軌制導車輛的整體性能,以達到車體性能最優化。

2 結構

對懸掛式有軌制導車輛車體進行靜態分析,可以得到車體框架的變形和應力分布,針對結構的薄弱環節進行設計參數優化與改進,以提高車體結構的可靠性[6]。

懸掛式有軌制導車輛主要由車體、動力牽引單元、升降驅動單元、機械夾緊單元、導向單元、基礎控制裝置等組成。其中,車體結構如圖1所示。

圖1 車體結構

車體結構及性能特點如下:

(1) 車體主要基于兩個由Q235B碳素結構鋼焊接而成的異型架、一對連接橫梁、兩個對稱連接板通過螺栓連接而成;

(2) 主異型架、副異型架上分別有橫梁、連接板,以及升降驅動單元和機械夾緊單元的安裝孔;

(3) 橫梁上設有對稱導向輪裝置,使有軌制導車輛在單軌上能夠正常行駛并及時導向,進而可以避免側翻;

(4) 動力牽引單元及基礎控制裝置安裝于車體內部,充分利用結構空間。

3 力學性能分析

應用CREO軟件創建懸掛式有軌制導車輛車體參數化三維數學模型,同時配置CREO軟件與ANSYS軟件的數據接口,將參數導入ANSYS Workbench軟件[7]。定義車體的材料為Q235B碳素結構鋼,選擇SOLID 185單元進行網格劃分,網格尺寸為5 mm,共劃分得到817 226個節點和362 324個單元。

考慮懸掛式有軌制導車輛最大負載時的接觸與受力情況,選擇超常載荷彎曲工況進行靜力學性能分析與后處理。限制四個行走輪安裝座位置的所有自由度,車體所受載荷主要由貨箱、差速器、升降驅動單元、導向輪等部件的質量,以及車體自身質量組成。車體所受載荷與約束如圖2所示。

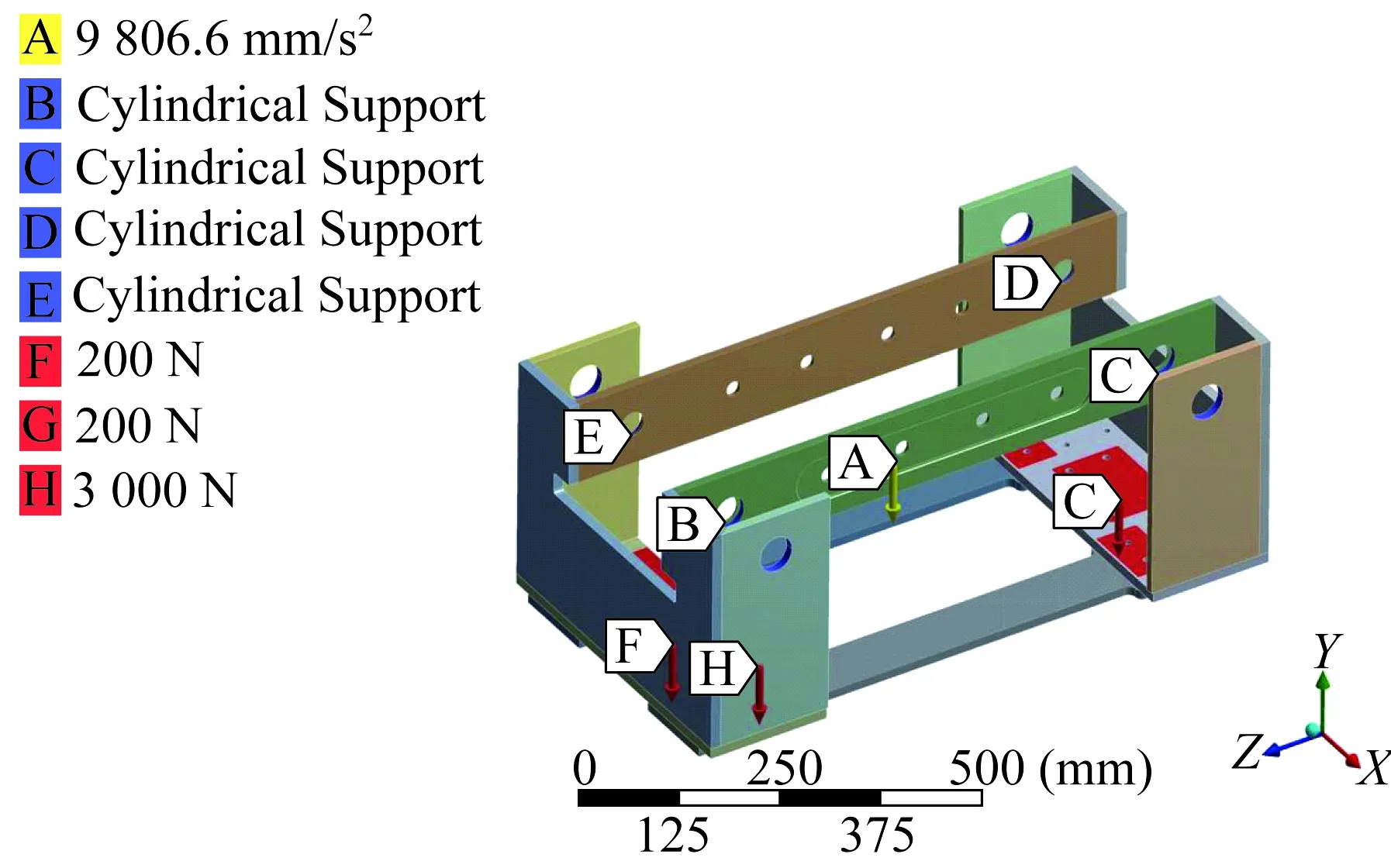
圖2 車體載荷與約束

對車體進行靜強度分析,車體的變形云圖和等效應力云圖分別如圖3、圖4所示。從圖3中可以看出,車體最大變形產生于底部兩連接板內側中間部分,最大變形量為3.365 4×10-2mm,遠小于1 mm。從圖4中可以看出,車體最大等效應力產生于異型架底部兩側位置,最大等效應力值為9.873 3 MPa,遠小于Q235B碳素結構鋼的屈服強度235 MPa。

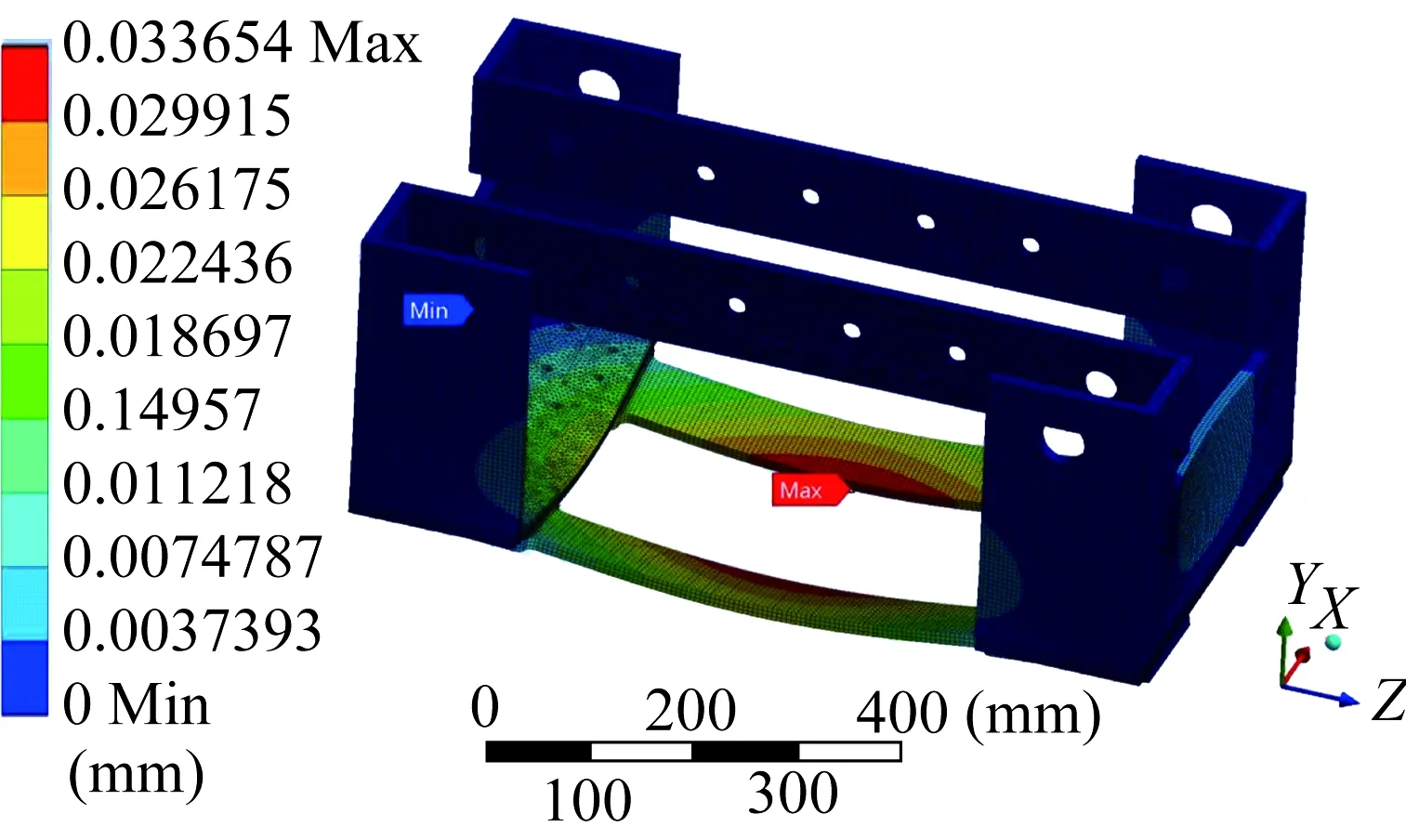
圖3 車體變形云圖

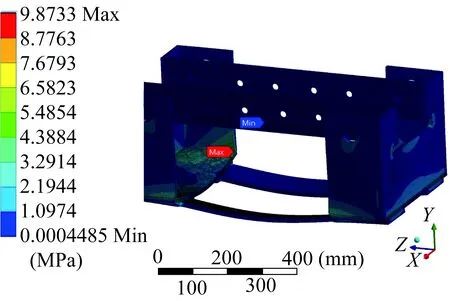
圖4 車體等效應力云圖

對車體進行模態分析,得到車體的前六階模態頻率和前三階固有頻率所對應的振型、最大變形。車體前三階模態振型如圖5所示,車體前六階模態頻率和最大變形量見表1。從圖5、表1中可以看出,車體的一階固有頻率為232.45 Hz,遠高于軌道的激勵頻率,軌道的激勵頻率低于100 Hz[8]。由此可見,能夠避免懸掛式有軌制導車輛在搬運過程中發生共振現象,使懸掛式有軌制導車輛具有較高的穩定性與可靠性。

綜合以上分析可以看到,車體的變形和等效應力均有較大的設計余量,且結構穩定,安全因數較高,有較大的優化設計空間。根據輕量化設計原則,可以考慮減小異形架組焊板截面尺寸,簡化車體結構,在保證車體穩定性的基礎上進行優化設計。

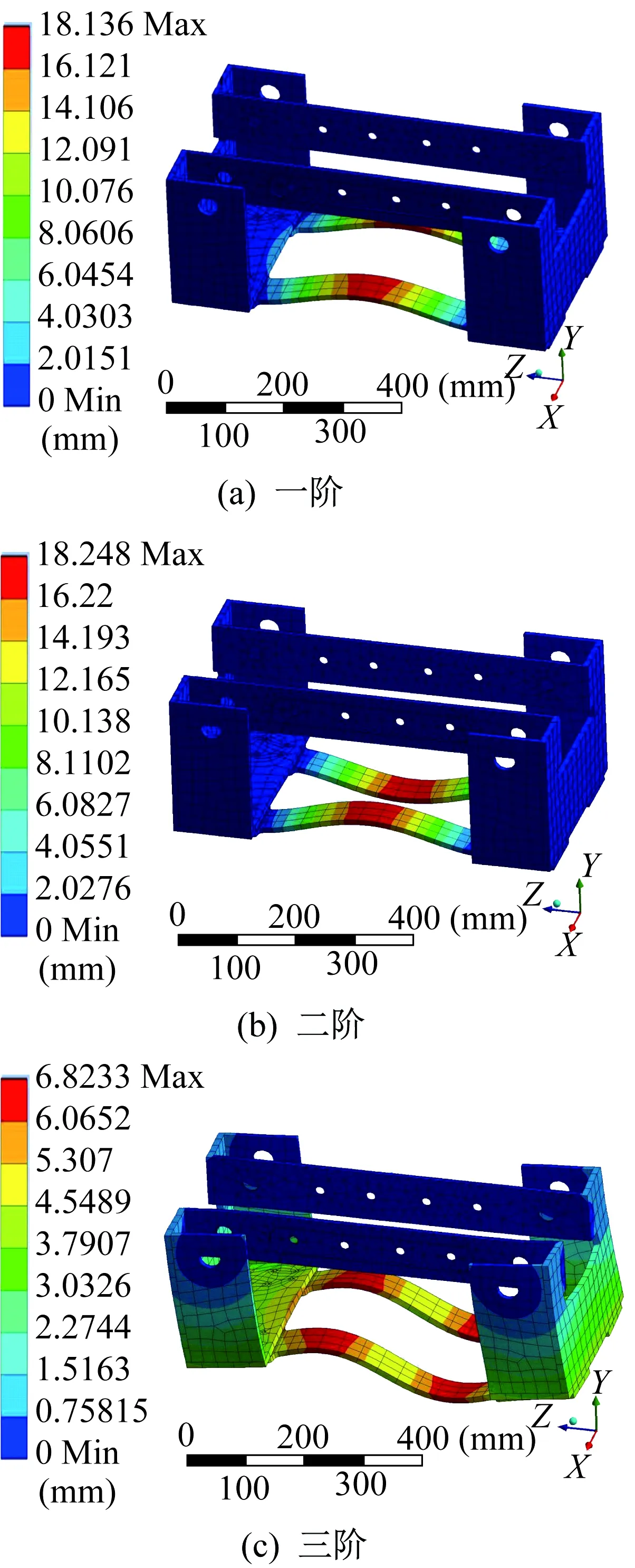
圖5 車體前三階模態振型

表1 車體前六階模態頻率和最大變形量

4 設計目標參數

在實際項目設計中,需要在物理模型中抽象出能夠體現設計要求的一組數學表達式,即結構優化設計數學模型,主要包含設計變量、目標函數、約束條件三大要素[9]。數學表達式如下:

Findx=[x1,x2,…,xn]T

MinF(x)=f[x1,x2,…,xn]

s.t.Hj(x)=0j=1,2,…,k

Gi(x)≤0i=1,2,…,m

xia≤xi≤xibxi=1,2,…,n

式中:x為設計變量;n為設計變量數量;F(x)為優化目標函數;Hj(x)為等式約束條件;Gi(x)為不等式約束條件;xi為第i個所選設計參數;xia、xib分別為設計變量的上限、下限。

定義異型架底板厚度為P1,兩側板厚度為P2,連接板厚度為P3。根據上述靜力學分析可知,車體框架的最大變形和最大應力分別產生在異型架的底板與側板、底板與連接板的連接位置,異型架底板、兩側板、連接板的厚度對車體的變形和應力影響較大,因此將異型架底板厚度P1、兩側板厚度P2、連接板厚度P3設置為設計目標參數,如圖6所示。

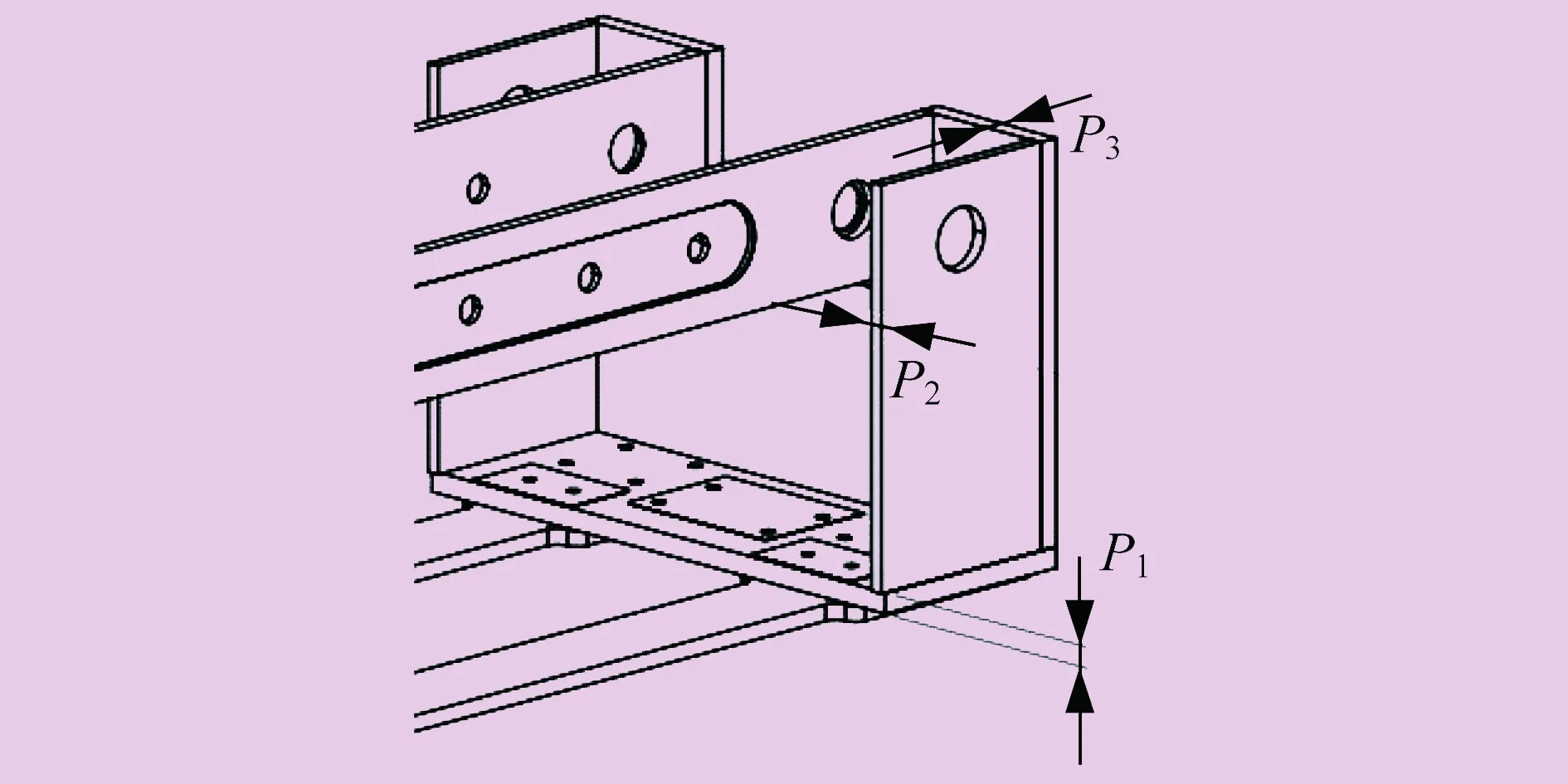
圖6 設計目標參數

為減小車體變形量δ和應力σ,將車體質量M(x)、最大變形量δmax(x)、最大等效應力σmax(x)的最小值作為輸出目標參數。其中,一階頻率f1(x)、二階頻率f2(x)、三階頻率f3(x)均需高于軌道的固有頻率(100 Hz)[8]。將設計目標參數和輸出目標參數代入前述數學表達式,建立目標參數優化數學模型:

Findx=[P1,P2,P3]T

MinF(x)=[M(x),δmax(x),σmax(x)]

s.t.M(x)=Mmin(x)

δ<δmax(x)

σ<σmax(x)

f1(x)>100

f2(x)>100

f3(x)>100

設計目標參數的取值范圍見表2。

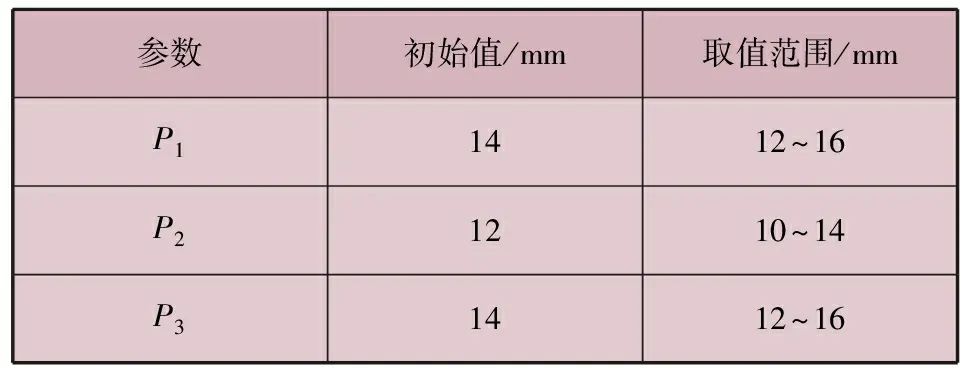
表2 設計目標參數取值范圍

5 靈敏度分析

參數靈敏度分析是一種反映設計變量對目標變量敏感程度的分析方法[10]。在懸掛式有軌制導車輛車體參數優化過程中,需要對多個設計變量進行參數調整,以便找出對目標函數影響較大的關鍵設計參數。通過靈敏度分析,能夠快速確定最為直接的主要設計變量。設計目標參數對目標函數的靈敏度分析結果如圖7所示。由圖7可以直觀地看出優化過程中設計目標參數對車體質量、最大變形量、最大等效應力的相關程度、敏感因數、敏感程度。P1、P2、P3對車體質量的敏感因數依次為0.486 04、0.575 07、0.652 59,表明P3對車體質量影響程度較大,且呈正相關。P1、P2、P3對車體最大變形量的敏感因數依次為-0.877 49、-0.416 50、-0.250 55,表明P1對車體最大變形量影響程度較大,且呈負相關。P1、P2、P3對車體最大等效應力的敏感因數依次為-0.567 83、-0.675 53、-0.096 76,表明P1對車體最大等效應力影響程度較大,且呈負相關。

綜合靈敏度分析可知,異型架底板厚度和連接板厚度對車體質量、最大變形量、最大等效應力影響較大,因此,在優化設計過程中要優先考慮選擇較小值,這樣有利于實現對懸掛式有軌制導車輛車體的結構優化與改進。

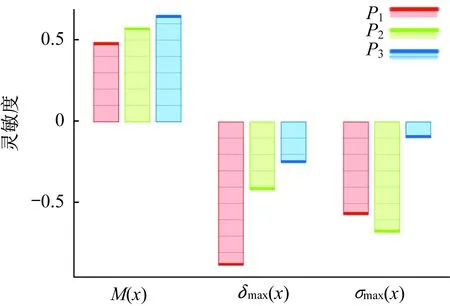
圖7 靈敏度分析結果

6 響應面分析

響應面分析是一種能夠準確反映輸入參數與輸出參數之間相互作用關系的分析方法[11]。針對懸掛式有軌制導車輛車體模型,通過響應面分析,擬合出輸入的設計目標參數與輸出的目標函數之間的響應關系曲面,能夠更加直觀地獲得設計目標參數對目標函數的響應分布、響應趨勢和每個設計點的響應。設計目標參數對車體質量、最大變形量、最大等效應力的響應依次如圖8、圖9、圖10所示。

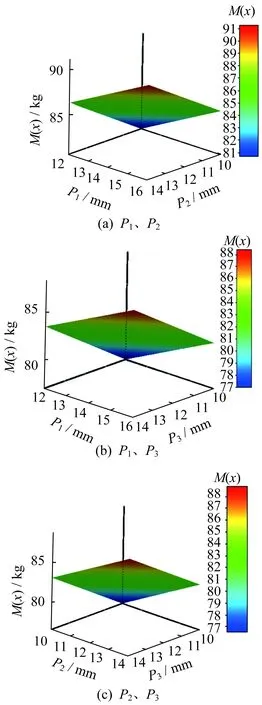
圖8 設計目標參數對車體質量的響應

由圖8可知,車體質量隨P1、P2、P3增大而逐漸增大,其中P3對車體質量影響程度較大,P3應取較小值。

由圖9可知,車體最大變形量隨P1、P2、P3增大而逐漸減小,最大變形量遠小于1 mm,因此,為使車體質量最小,這三個設計目標參數應盡可能選取較小值。

由圖10可知,車體最大等效應力隨P1、P3增大而減小,隨P2增大先逐漸減小,當P2達到11.5 mm以后又逐漸增大。為減小車體最大等效應力,P2應選擇為12 mm。

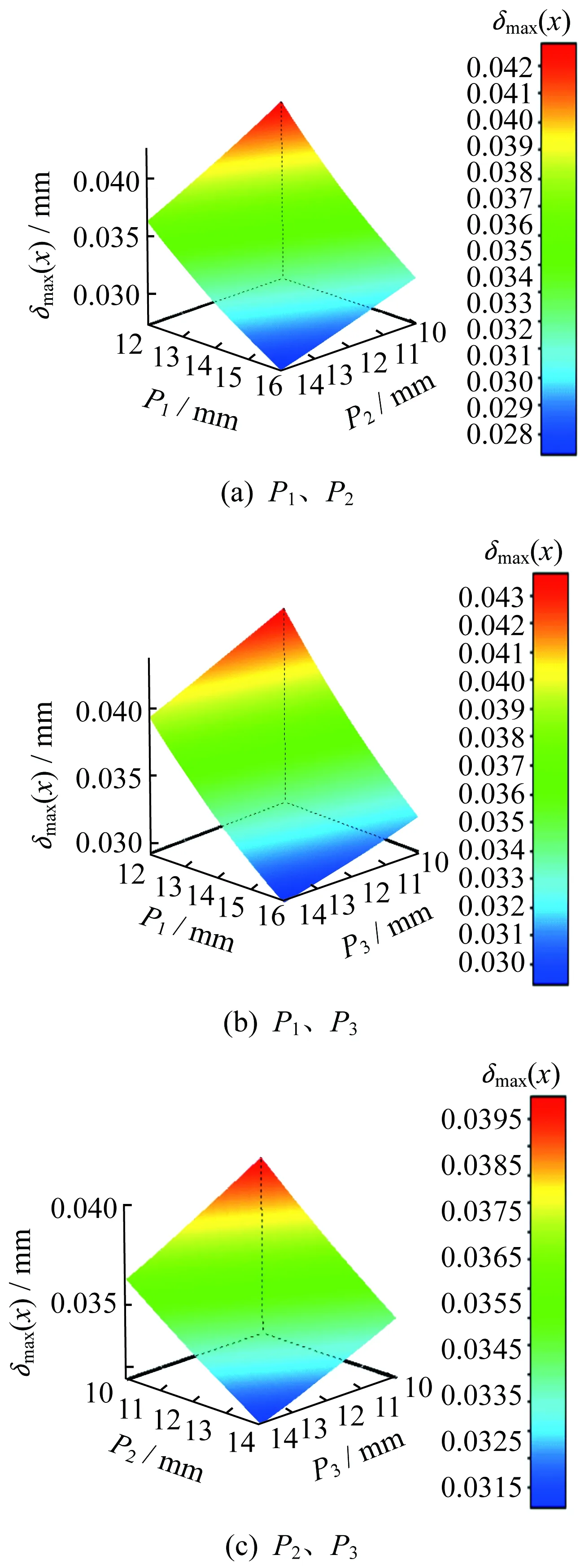
圖9 設計目標參數對車體最大變形量的響應

7 候選方案

在滿足所有約束條件的前提下,應用ANSYS Workbench軟件DesignExplorer模塊,根據優化設計數學模型,自動篩選出車體質量最小、最大變形量最小、最大等效應力最小的三組優化設計最大目標參數最優的候選方案,并對三個設計目標參數進行修正。候選方案見表3。由表3可知,三個設計目標參數優化后,使懸掛式有軌制導車輛車體總質量減小,車體最大等效應力有較小幅度增大,但未超出允許范圍。綜合上述分析可知,多目標參數優化設計不僅能夠滿足車體在強度和剛度方面的要求,而且使車體尺寸更加合理,優化效果顯著。

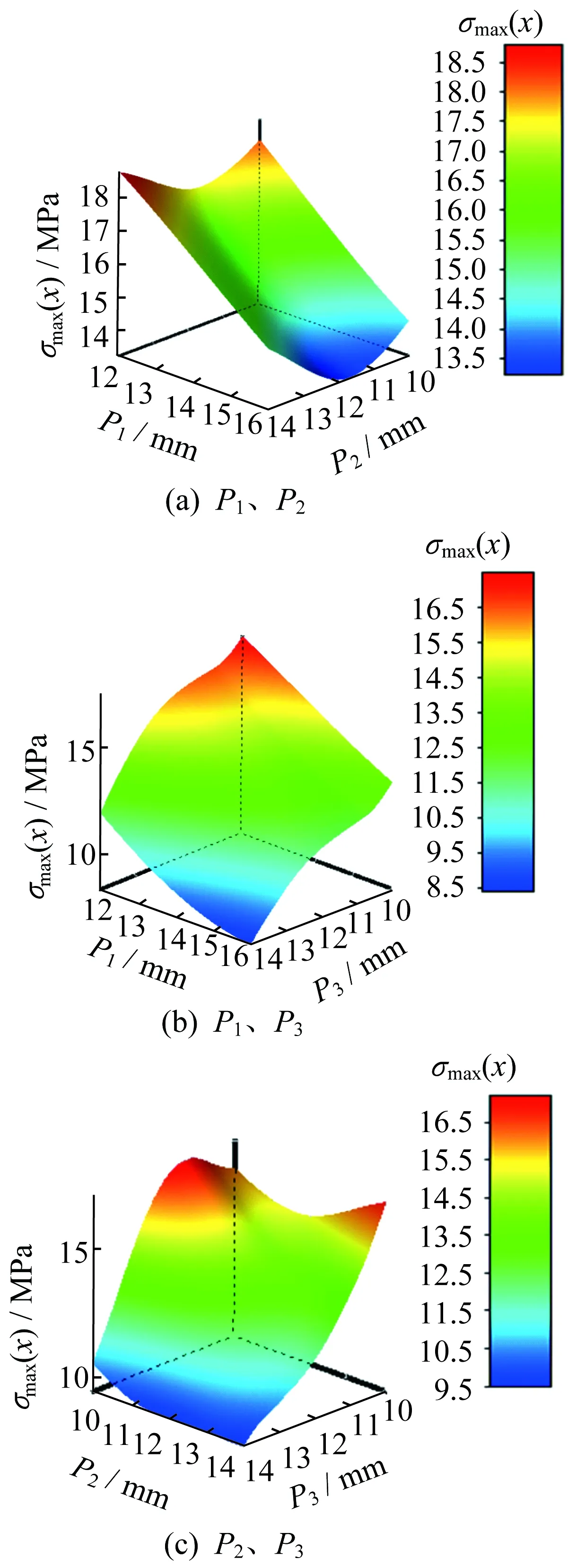
圖10 設計目標參數對車體最大等效應力的響應

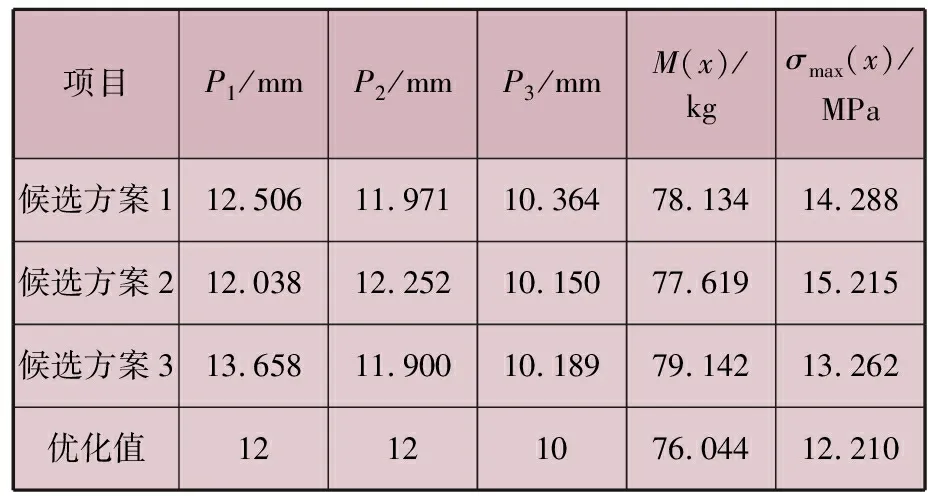
表3 候選方案

8 優化后車體性能評估

將確定的優化值輸入ANSYS Workbench軟件,應用DesignExplorer模塊在相同的約束和載荷條件下再次進行靜力學分析,得到優化后懸掛式有軌制導車輛車體與原車體的力學性能對比,見表4。

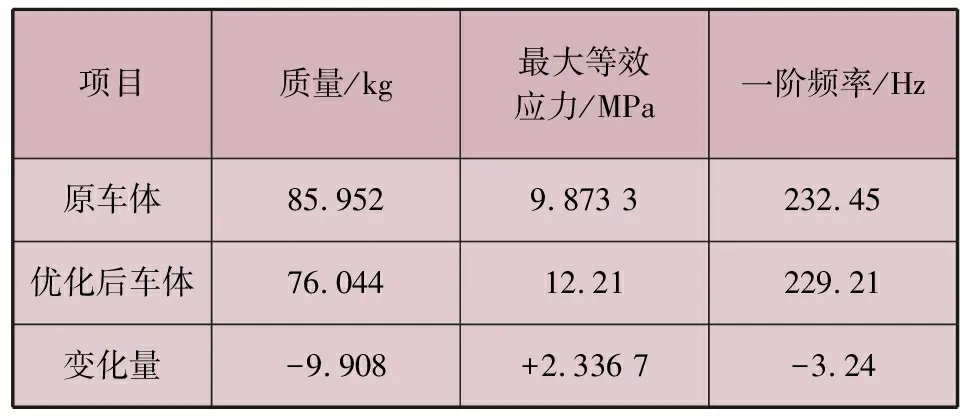
表4 車體力學性能對比

由表4可知,優化后車體質量較原車體質量減小了11.53%,輕量化效果顯著。最大等效應力增大了23.67%,但仍遠小于材料的屈服極限235 MPa,力學性能顯著提升。一階固有頻率降低了3.24 Hz,且仍遠離軌道的固有頻率,在運行過程中可以有效避免共振發生,保證懸掛式有軌制導車輛運行的可靠性。

9 結束語

通過CREO軟件與ANSYS軟件建立數據接口,對懸掛式有軌制導車輛車體進行多目標參數優化設計,由靜力學分析、模態分析、靈敏度分析、響應面分析得到車體關鍵尺寸與車體質量、最大變形量、最大等效應力間的關系曲線,通過篩選得到優化方案。優化方案與原車體對比,車體質量減小了9.908 kg,減小幅度為11.53%,輕量化效果顯著。最大等效應力增大為12.21 MPa,但仍遠小于材料的屈服極限。多目標參數優化設計使車體的結構和尺寸更加合理。