基于旋轉磁鐵的電磁學分析
唐 豪 謝 瑜* 楊佳東 楊占金
(新疆農業大學,新疆 烏魯木齊 830052)
2021 年國際青年物理學家錦標賽(IYPT)的第2 賽題為“旋轉磁鐵(Circling Magnets)”:將直徑不同的紐扣磁鐵貼附到圓柱形電磁的兩端,將其放置在鋁箔上或物體會開始旋轉。探究相關參數如何影響運動。可以引申到相關參數對電動機的影響等實際問題。針對類似的簡易電動機模型,我們可以從法拉第對簡易電動機的理論分析那里得出一個動力來源以及相關電流分析,但是相對于本文的“旋轉磁鐵”其研究因素較少,模型建立也大不相同。
1 基礎理論模型及其求解
1.1 運動軌跡的基礎分析
通過幾個簡單的預實驗以及對模型的簡單分析發現可以發現在一定條件下運動軌跡半徑與該實驗的相關物理參數無關,只與磁鐵- 電池所形成的聯合體的幾何關系相關如圖1 所示。在這里可以近似認為磁鐵- 電池聯合體是剛體,并且沿軸對稱,而對稱軸為正極端頂面與負極端底面的圓心連線所構成的直線。設吸附在正極端上的磁鐵半徑為R1,厚度為h1,所受到的徑向摩擦力為f1,吸附在負極端上的磁鐵半徑為R2,厚度為h2,所受到的徑向摩擦力為f2。電池半徑為R0,長度為h0。兩接地點的之間的距離為hΔ,運動軌跡半徑為R。
對磁鐵- 電池聯合體進行幾何分析如圖1,物體受到的軸向摩擦力充當向心力使其做圓周運動,當滿足做圓周運動所需的向心力小于最大靜摩擦力的時候,物體做圓周運動的軌跡半徑可以直接由磁鐵- 電池聯合體的幾何關系得出
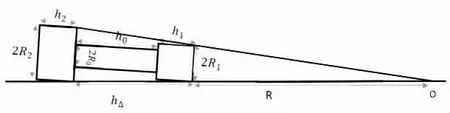
圖1 磁鐵- 電池聯合體與半徑的幾何關系

再通過對磁鐵- 電池所構成的聯合體進行分析,可以得出做圓周運動軌跡的半徑R。

聯立(1)、(2)式,解得:
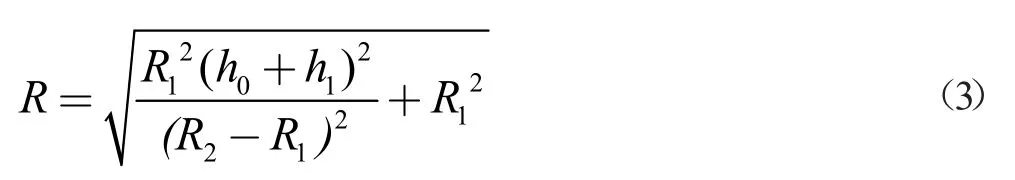
故磁鐵- 電池聯合體在滿足做圓周運動所需的向心力小于最大靜摩擦的時候,其運動半徑取決于該聯合體的幾何關系,與其他無關。
1.2 運動條件及聯合體力矩的分布
當磁鐵- 電池聯合體放在鋁箔上形成回路時,由于電磁內阻很小,以及正負極兩端吸附的磁鐵電阻微弱,而鋁箔在這里充當導線作用電阻也很小。因此形成回路后,會有很大的電流從正極吸附的磁鐵中心流出,并從其邊緣流出,其方向與磁鐵表面磁場方向垂直,所以同時在磁鐵表面電流受到安倍力FI作用,而電流對磁鐵的反作用力F-I作為第一個動力源,如圖2 所示。電流再通過下方鋁箔,鋁箔上有磁場分布,因此下方鋁箔將受到安倍力的作用,因此會反饋給該聯合體一個反作用安倍力,作為第二個動力來源。電流再由負極端磁鐵邊緣流向中心,其方向與磁鐵表面磁場垂直,所以同時在磁鐵表面產生電流安倍力力矩作用,電流對磁鐵的反作用力矩作為的三個動力來源。

圖2 兩端N 極朝外的力矩分布情況
在磁鐵同極朝外的情況下,上述三個動力源作用于同一方向,聯合體才能正常做圓周運動。在異極朝外的情況,三個動力源提供的動力不足以支持其運動。同時當該聯合體做圓周運動詞正負極兩端磁鐵旋轉切割磁場,所以在正負極兩端會產生反向感應電動勢。下方鋁箔有磁場分布,所以當物體運動時,鋁箔切割磁場,產生反向感應電動勢。同時鋁箔表面于聯合體之間還有滾動摩擦力作用,提供阻力力矩作用。所以對于該聯合體的力矩分布情況如圖2 所示。
因此,磁鐵- 電池聯合體的運動情況為:從靜止開始做加速運動,但是隨著角速度的增大,產生的反向感應電動勢逐漸增大,從而逐漸減小回路中的電流強度和作用與磁鐵片以及鋁箔的安培力,使加速度逐漸減小,最后使安倍力力矩與阻力力矩平衡,角速度也不再增加。
1.3 物體力矩分析及物體公轉速度
設正極端的磁鐵半徑為R2,磁鐵表面的法向磁感應平均強度為B2。負極端的磁鐵半徑為R1,磁鐵表面的法向磁感應平均強度為B1。則兩磁鐵產生的力矩為:
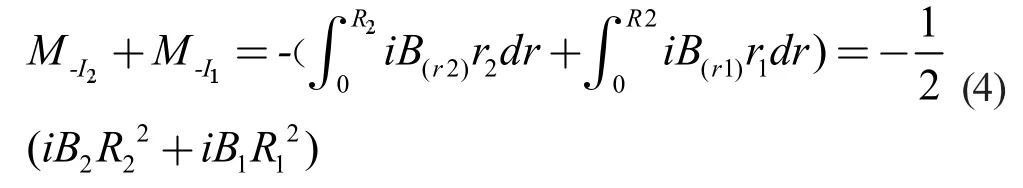
對于鋁箔而言,其導電長度為h⊿,通電鋁箔上其磁場平均強度記為BL,則鋁箔所提供的力矩為
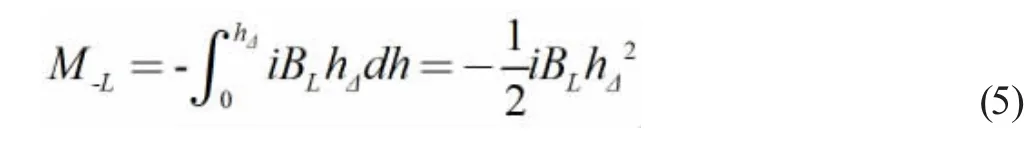
當物體自轉角速度為ω0時,記產生的反電動勢ε' ,則有

設回路總電阻為r總,可以得出該回路中的電流為

其中ε0為電源電動勢。
設該聯合體所受到的阻力矩為;Mf,磁鐵- 電池聯合體的轉動慣量為J,則物體的角加速度為
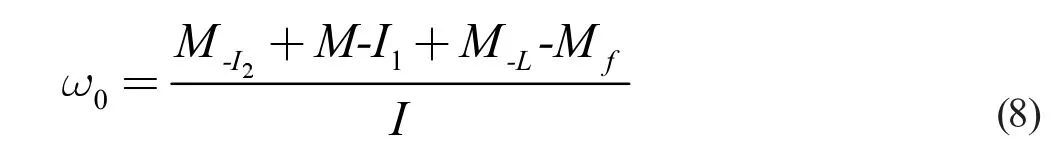
該聯合體在運動中一直保持滾動的形式,所以其阻力主要來源于滾動摩擦,設負極端產生的滾動摩擦力為f1,正極端產生的滾動摩擦力為f2,則
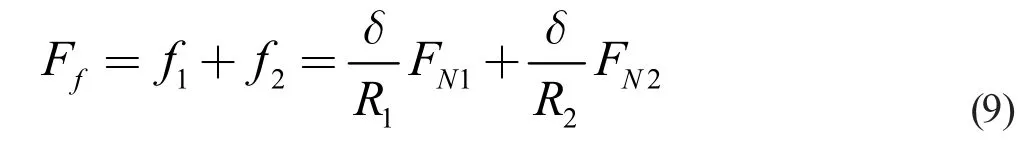
其中δ 為滾動摩阻系數,只與接觸面材料有關,FN1為正極端磁鐵的正壓力FN2為負極端磁鐵的正壓力,所以滾動摩擦產生的力矩為
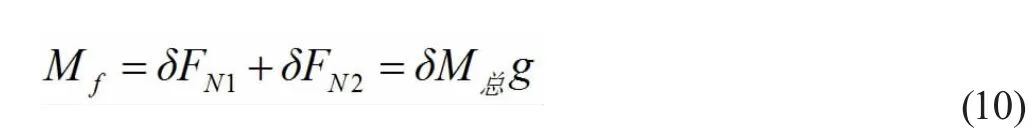
設兩磁鐵質量分別為m1和m2,電池質量為m0則有
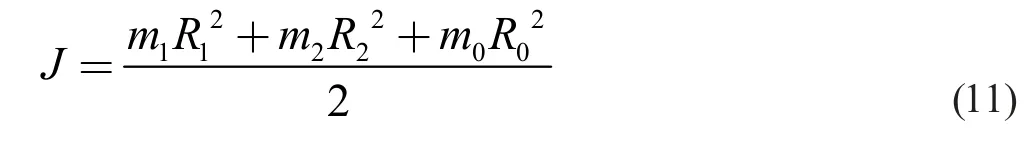
對物體所受的總體力矩分析
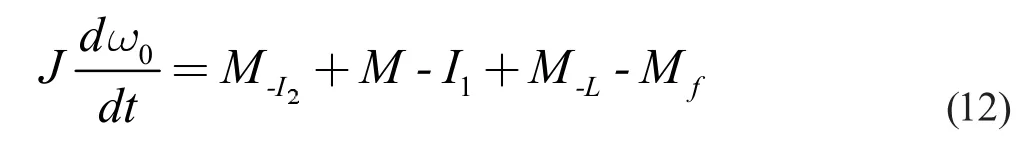
聯立式(4)- 式(11),整理可得

求解該微分方程可得

其中相關參數k,b 為
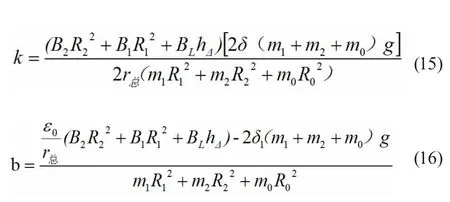
分析式(14)- 式(16) 可以得知物體的最大自轉角速度ωmax為

根據圖3,由于該聯合體運動屬于純滾動,所以可以由式(17)推出公轉角速ω1度及其吸附在正極端磁鐵的公轉速度v1
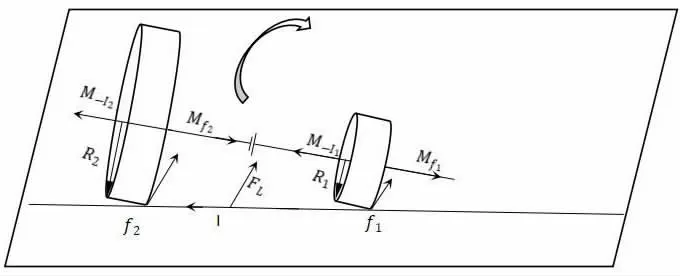
圖3
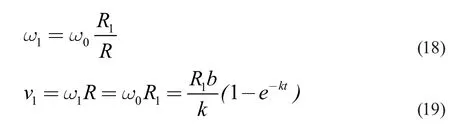
則該物體極限速度vmax
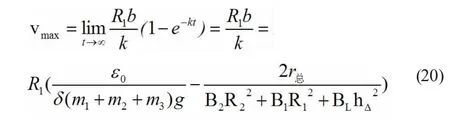
通過上面三式可以知,影響ωmax的獨立參數有ε0、r總、m1、m2、B2、B1、BL、m0以及聯合體幾何關系;而影響ω0的因素除此以外還有J,所以轉動慣量J 只影響其自轉角速度增大的快慢;同樣的有,影響聯合體最終的線速度有幾何關系、電源電動勢,質量,各處磁場分布情況以及總電阻。
1.4 安倍力隨電流分布情況
對于鋁箔而言,電流在鋁箔上非直線流向,在鋁箔上的曲線電流兩端各自取一小段微元。對于這兩小段微元產生的安倍力進行分解,分解為延軸向以及垂直軸向,這樣延軸向的安倍力分力相互抵消,既可以等效為延軸向電流計算,說明鋁箔產生的安倍力力矩與電流在鋁箔上的分布無關。
2 實驗探究
2.1 實驗設計
按照要求,實驗器材選取1.5v 的7 號干電池、半徑不同的兩種紐扣磁鐵、一張鋁箔、水平儀、刻度尺、攝像機、萬用表。實驗過程通過攝像機進行記錄,并用Tracker 軟件對視頻進行分析處理,通過追蹤磁鐵的位置,得到角速度隨時間變化的數據。再通過Origin 軟件對數據進行圖像化處理。
為了實現題目要求得到預期實驗效果,需要做以下準備:
(1)需要用水平儀提前調整實驗裝置的傾斜度,為了保證實驗不受重力的影響;
(2)使鋁箔表面清潔,避免回路電阻無故增大;
(3)實驗記錄時間不宜過久,因為隨著實驗的進行電源電動勢逐漸下降,內阻逐漸上升,可能會導致與預期效果不符;
該實驗裝置的優點在于,對無關變量嚴格控制,利用軟件進行測量減少人為誤差。
2.2 實驗結果
在滿足實驗前準備的前提下,選取規格為10.5×44.5mm 的1.5v 干電池,以及兩顆尺寸分別為20×10mm、10×10mm 的紐扣磁鐵。用萬用表對多組進行不同時長實驗的電池電壓進行測量,發現平均在14s 左右電壓出現了明顯的下降,所以實驗記錄時長不宜超過14s。記錄10 組重復實驗的ω-t 實驗數據,并得到10 組數據形成的散點圖與理論曲線對比如圖4。得到的R 值為0.97692,接近與1,與理論曲線擬合較好。故可以粗略的認為該物體運動的角速度隨時間變化滿足式(18)。而產生誤差的原因在于磁場強度不能細致的測量,實驗過程中電源電動勢的變化。
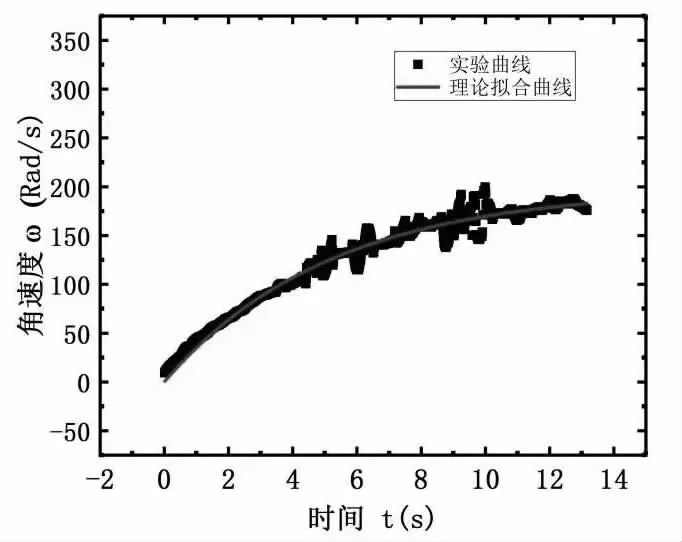
圖4 實驗曲線與理論擬合曲線的對比
3 結論
在該實驗構成的模型中,磁鐵- 電池聯合體在各種力矩的作用下從靜止開始運動,角加速度逐漸減小,角速度呈指數衰減式增長。影響該運動的參數有電源電動勢,轉動慣量,磁場強度,總電阻等。而由于實驗過程中能量變化難以測定,所以本文暫為對此進行深入的探究。

