一類帶有多時滯的中立型奇異馬爾科夫跳變系統的隨機穩定性研究
龍少華 周麗娟
(重慶理工大學 理學院,重慶 400054)
1 概述
隨著人類社會的進步和現代控制理論不斷深入的發展,在包括航空航天、化學工程、網絡、電力和經濟等在內的諸多領域中,人們發現了廣義系統的許多應用實例,如動態投入產出模型、紐曼模型、受限機器人模型以及核反應堆模型等。近幾十年來,廣義系統一直是學術界研究的熱點領域[1-3]。
另一方面,時滯是自然界中廣泛存在的一種物理現象。從工程技術、物理、化學反應、生物醫學等領域中提出的數學模型常常帶有明顯的滯后量。例如,在遠程控制系統中,計算機網絡傳輸誘導的信息延遲使得系統經常出現信息滯后現象。在實際工程系統中,由于元器件老化、測量滯后等原因,在其運行過程中也常常存在滯后現象。因此,時滯系統也一直是學術界研究的熱點領域[1-4]。
此外,有些實際系統,在描述其數學模型時,我們不僅需要考慮狀態向量的時滯,還需要考慮狀態向量的導向量的時滯,即時滯不僅存在于狀態向量中,還存在于狀態向量的導向量中。我們把這種系統稱為中立型系統。中立型系統是一類非常重要的時滯系統,它有著廣泛的應用背景,如部分元等效電路系統、無損耗傳輸系統、熱交換器系統等。近幾十年來,對中立型系統的研究也得到了飛速的發展[5-9]。
目前,對于帶有多時滯的中立型奇異馬爾科夫跳變系統的隨機穩定性的研究還不完善。
本文將對一類帶有多時滯的中立型奇異馬爾科夫跳變系統的隨機穩定性進行研究。
2 準備知識
在本文中,我們考慮一類多時滯的中立型奇異馬爾科夫跳變系統的隨機穩定性,系統的模型如下:
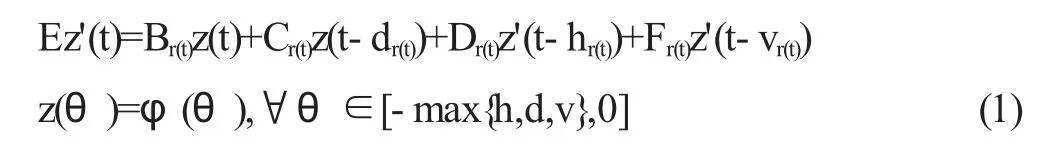
其中z(t)是n 維列向量,代表系統的狀態向量。{r(t),t≥0}是右連續的馬爾科夫過程,它的狀態為有限個且假定其取值于集合χ={1,2, ,N}。此外,我們假定從狀態i 到狀態j 的轉移速率bij滿足下式:
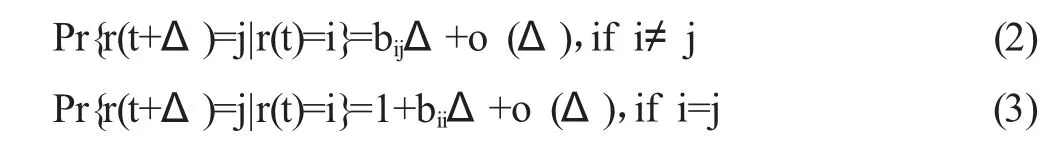
其中bij>0(i≠j)和bii=-bi1-bi2-...-biN。
在(1)式中,hj>0(j∈χ),dj>0(j∈χ)和vj>0(j∈χ)表示系統的 時 滯 且 都 是 常 數,h=max {h1,h2,...,hN},d=max{d1,d2,...,dN},v=max{v1,v2,...,vN}。矩陣E、Bj>0(j∈χ)、Cj>0(j∈χ)、Dj>0(j∈χ)和Fj>0(j∈χ)都是已知的n×n 矩陣。我們假定矩陣E 的秩為m。
在后面,我們將把系統(1)轉化成帶有時滯的的奇異馬爾科夫跳變系統。為了方便后面的討論,我們先給出一些有關奇異馬爾科夫跳變系統的定義。
定義1[3]:稱系統Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是正則的,如果對于每一個i∈χ,都有det(sE-Bi)不恒等于0。
定義2[3]:稱系統Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是無脈沖的,如果對于每一個i∈χ,都有deg(det(sE-Bi))=rank(E)。
定義3:稱系統Ez′(t)=Br(t)z(t)+Cr(t)z(t-dr(t))是隨機穩定的,如果對于任意的初始條件(r(0),φ(·)),系統的解z(t)滿足
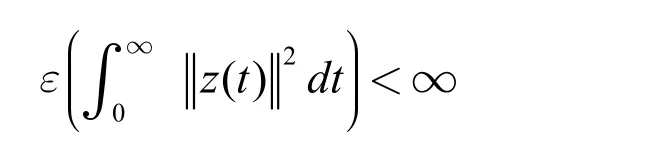
3 主要結果
在本文中,我們考慮如下情形:對于每一個i∈χ,總存在矩陣Wi和Hi分別滿足
WiE=Di和HiE=Fi。
對于系統(1),我們可得如下的定理。
定理1. 給定n×n 矩陣K 滿足KE=0 和rank(K)=n-m。稱系統(1)是隨機穩定的,如果存在矩陣Q1>0,M1>0,Y1>0,Pi>0(i∈χ),U1>0 和Si(i∈χ)滿足
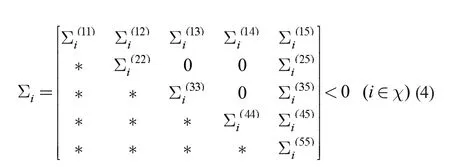
其中

證明:我們首先證明系統(1)是正則和無脈沖的。
根據(4)式,我們可得
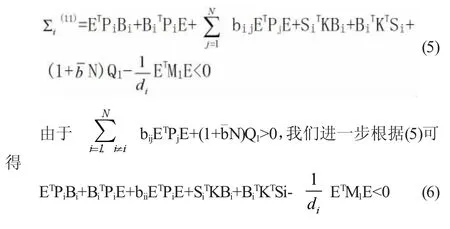
注意rank(E)=m<n, 我們可以找到兩個矩陣G1和G2滿足

定義
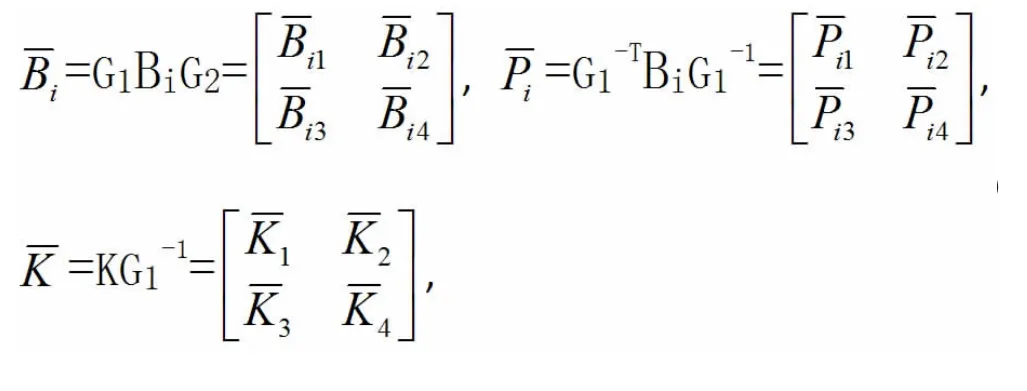
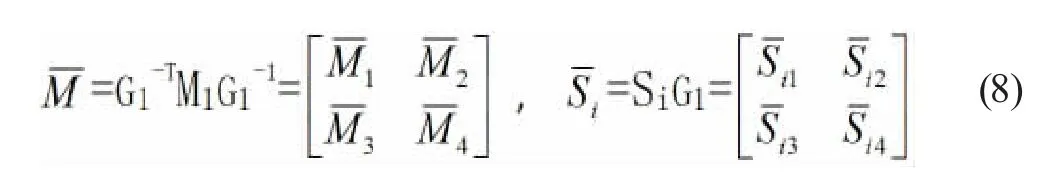
用G1T和G1分別左乘和右乘(6)式,我們可得

注意到WiE=Di和HiE=Fi,令γ(t)=Ez′(t),可得系統(1)等價于下面的系統:
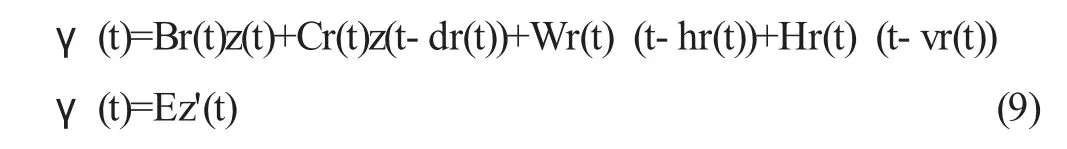
可以看出,系統(8)等價于下面的系統:

我們利用下面的李雅普諾夫泛函來幫助我們證明上述系統是隨機穩定的。
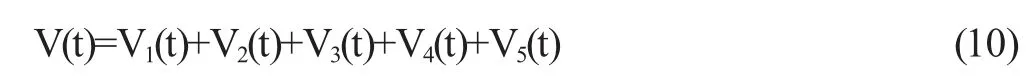
其中
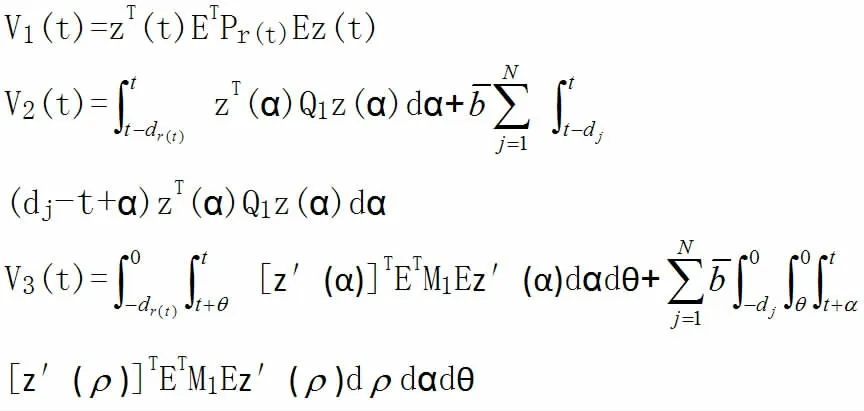
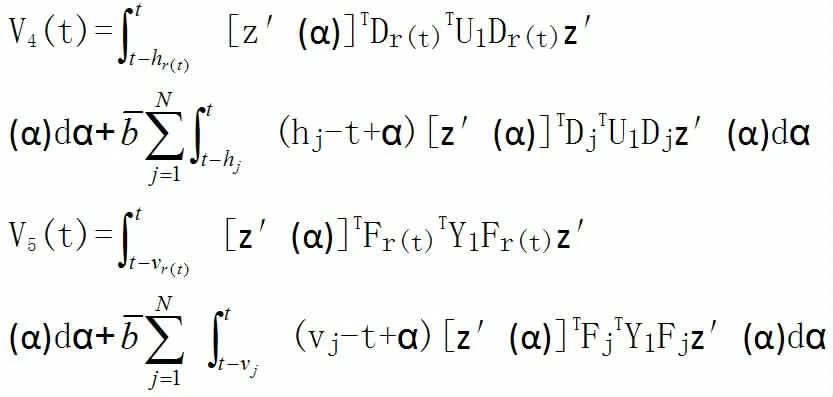
由上式我們可得

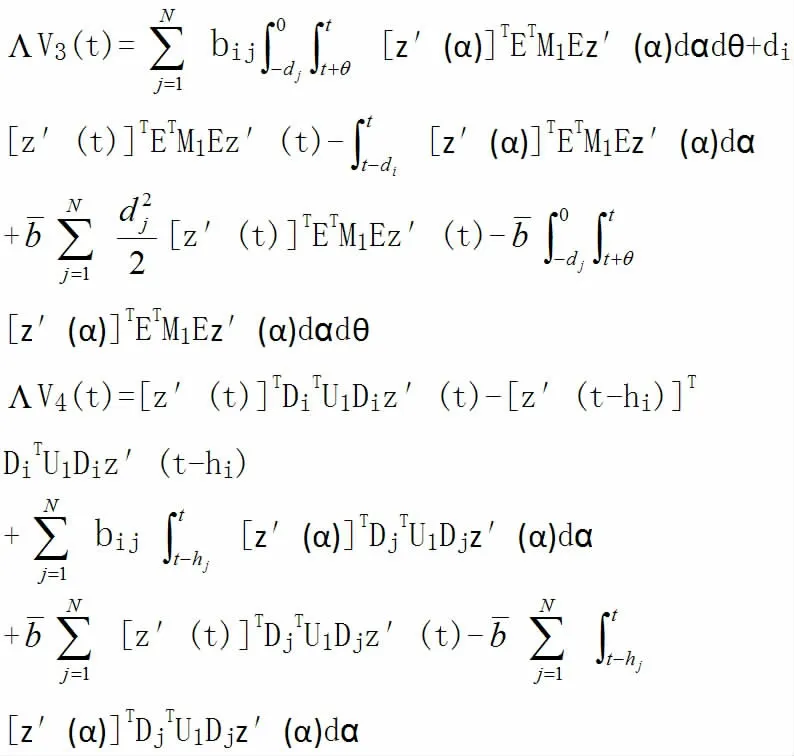
注意KE=0,我們可得2[Ez′(t)]TKTSiz(t)=0,也就是
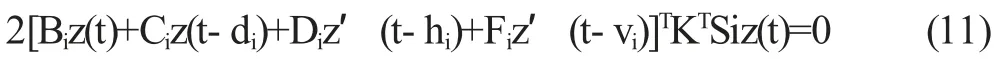
根據(10)-(11) ,我們可得
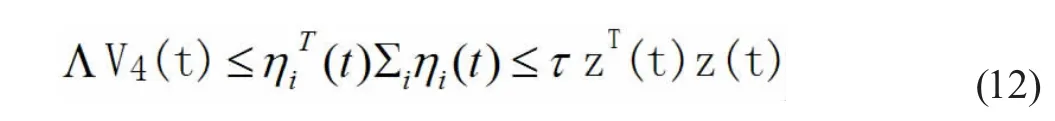
其中
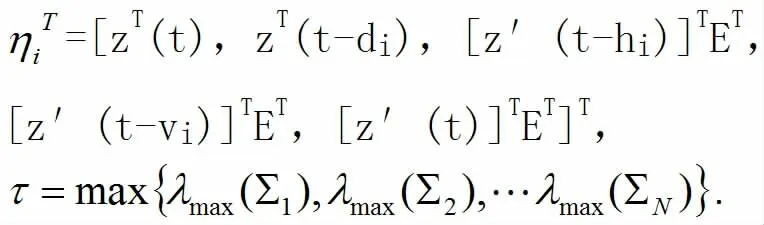
注意τ<0,由(11)可得
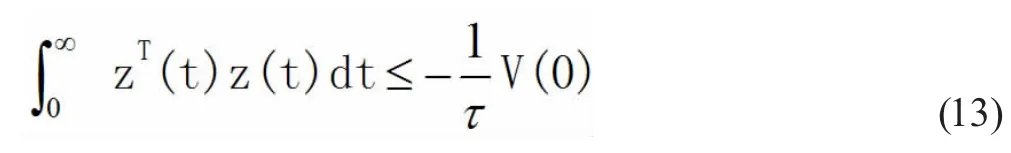
所以,根據定義3 可得系統(1)是隨機穩定的。證畢。
4 算例
考慮系統(1),假定系統中的參數如下:

利用Matlab 線性矩陣不等式工具箱,我們可得線性矩陣不等式(3)是可行的。這說明了系統(1)是正則、無脈沖且隨機穩定的。

