零售商風險規避下基于聯合契約的雙渠道供應鏈庫存決策模型

朱寶琳,薛 林,戢守峰,邱若臻

(東北大學 工商管理學院,沈陽 110167)

隨著互聯網和電子商務的發展,越來越多的制造企業采取線上直銷的方式作為產品新的營銷渠道。傳統零售和線上直銷相結合的雙渠道模式已成為許多制造商的主要運營模式。蘋果、聯想、耐克等都在傳統零售渠道的基礎上迅速加入了線上直銷渠道,而戴爾除了在自身網站上為顧客提供電腦的線上定制以外,還開辟線下門店銷售其產品。雙渠道模式不僅使制造商增加銷量,還能幫助企業降低成本和擴大市場占有份額,最終提升企業競爭力。但雙渠道模式對線下零售企業也造成了較大的威脅,導致傳統零售商對線上直銷采取抵制態度,最終造成庫存沖突和雙重邊際效應。與此同時,雙渠道供應鏈成員依然會面對各種不確定性以及不確定性導致的風險問題。近年來,針對不確定條件下考慮風險偏好的雙渠道供應鏈庫存協調研究已引起企業界和學術界的重視。

雙渠道庫存管理是供應鏈管理的重要環節,對雙渠道供應鏈參與者的決策產生重要影響。庫存成本在供應鏈總成本中占有較大的比重,如何有效地管理雙渠道庫存并實現庫存成本減少是決策者所面臨的主要問題。與傳統供應鏈庫存管理相比,雙渠道供應鏈庫存管理面臨著渠道間的庫存競爭和各種不確定的問題,這些問題極大影響了供應鏈成員的決策。目前,雙渠道供應鏈的不確定性主要集中在制造商產出和市場需求不確定兩個方面。針對需求不確定下雙渠道供應鏈的庫存研究包括:Huang等[1]研究了隨機需求下由一個制造商和一個零售商組成的雙渠道供應鏈庫存決策及定價問題,利用Stackelberg博弈獲得零售商最優庫存因子、制造商最優庫存因子以及最優線上售價;張雨濛等[2]研究由制造商、分銷商和零售商組成的供應鏈庫存決策問題,分析了集中和分散情況下雙渠道供應鏈的最優庫存決策,運用結合數量彈性和收益共享的聯合契約進行協調;Yan等[3]構建了資金約束下供應商和零售商組成的雙渠道供應鏈決策模型,分析了供應商面對資金約束時的最優庫存量、價格及利潤;Zhou等[4]研究了在信息不對稱情況下由制造商主導的雙渠道供應鏈的最優決策問題,獲得了最優訂購量及價格;He等[5]研究了易腐蝕產品雙渠道供應鏈的庫存及定價問題,分析了集中和分散情況下的庫存和定價策略,通過收益共享和關稅合同實現了協調;Takahashi等[6]研究了具有生產和交付的雙渠道供應鏈庫存問題,通過馬爾科夫方法分析了庫存策略的有效性;Yang等[7]研究了考慮線上直銷和交貨時間的雙渠道供應鏈的庫存競爭問題,證明并分析了零售商最優訂貨決策和制造商的最優庫存決策;Alawneh等[8]研究了隨機需求下考慮倉庫容量和提前期的雙渠道供應鏈庫存模型,運用正態分布和均勻分布方法進行求解;Li等[9]研究了需求依賴庫存的雙渠道供應鏈庫存管理問題,通過多周期隨機動態規劃模型實現了最優庫存決策。針對產出不確定下雙渠道供應鏈庫存研究包括;Cai等[10]研究了產出不確定下供應商庫存管理問題,通過期權契約協調供應鏈并實現帕累托改進;Fang等[11]考慮產出不確定的兩條供應鏈之間的競爭模型,分析了產出不確定性和競爭強度水平對訂購數量的影響;Hu等[12]研究產需不確定下制造商和供應商的訂貨策略,利用折扣契約協調供應鏈。上述研究僅針對需求或產出不確定性對雙渠道供應鏈庫存決策的影響。目前,同時考慮產出和需求不確定下雙渠道供應鏈庫存研究方面的還鮮有展示。

供應鏈庫存管理還面臨著各種不確定性帶來的風險問題。在供應鏈的參與方表現為風險偏好,如風險規避等行為。通過對不確定和風險行為進行有效管理,有助于提高雙渠道供應鏈庫存的運營效率。CVaR(Conditional Value at Risk)方法是當前較為流行的風險測量方法,該方法不但在期望利潤和風險之間實現了平衡,而且在理論研究和實踐領域中得到廣泛的應用。近年來,基于CVaR 的供應鏈庫存研究已成為國內外學者研究重點,主要包括風險規避下單一渠道和雙渠道供應鏈庫存決策的研究。基于CVaR 的單一渠道供應鏈庫存協調研究包括:Qiu等[13]研究了基于報童模型的考慮風險規避的供應鏈魯棒決策問題,證明并分析了基于CVaR 的庫存最優決策;林強等[14]研究了基于CVaR 的供應鏈收益共享模型,證明并分析了集中和分散情況下風險規避零售商和風險規避制造商的最優庫存決策;Xu等[15]研究并分析了基于報童模型的帶有缺貨成本的CVaR 最優庫存決策;高婷等[16]通過CVaR 準則證明并分析了基于庫存的零售商最優訂貨決策及其實現條件。基于CVaR 的雙渠道供應鏈庫存決策的研究包括:Li等[17]研究了信息不對稱下制造商侵占行為對零售商風險規避行為的影響,并進一步分析了零售商的風險規避行為對雙渠道供應鏈最優決策的影響;徐兵等[18]利用條件風險值和均衡分析方法建立了制造商和零售商同為風險規避的雙渠道供應鏈最優決策模型,分析了風險規避行為對決策者最優訂購量的影響;Zhu 等[19]運用CVaR 的方法研究了雙渠道供應鏈庫存決策,通過改進的風險共擔契約協調雙渠道供應鏈;曲優等[20]構建了成員具有行為偏好及需求轉移的雙渠道供應鏈訂貨模型,并用納什博弈模型研究了行為偏好對成員最優訂貨策略的影響。

契約方法是供應鏈庫存協調的重要手段,一般包括收益共享契約、回購契約和風險共擔契約等。一般而言,傳統的單一契約模式不能實現帶有風險規避的雙渠道供應鏈協調,Xu等[21]證明單一契約不能實現帶有風險規避的雙渠道供應鏈的協調。因此,采用改進或聯合契約是目前雙渠道供應鏈協調的主要方式。針對供應鏈庫存契約協調的研究主要包括:朱寶琳等[22]研究了產需不確定下的三級供應鏈的協調問題,證明了風險共擔和GL 組合契約可實現協調;Jian等[23]研究了由供應商、制造商和零售商組成的三級供應鏈系統的協調問題,運用結合回購與風險分擔的聯合契約實現了協調;Li等[24]研究了考慮供應鏈成員風險偏好的雙渠道供應鏈的協調問題,運用改進的風險共擔契約實現供應鏈的協調;Wang等[25]研究了雙渠道供應鏈的協調問題,提出了雙向收益共享契約可實現雙渠道供應鏈的協調;Xie等[26]研究了需求不確定下雙渠道供應鏈的契約協調,運用改進的收益共享契約實現供應鏈的協調;Zhang等[27]研究了需求和生產成本擾動下的雙渠道供應鏈協調問題,提出了聯合契約可以實現供應鏈的協調;Jiang等[28]運用CVaR 方法研究了零售商風險厭惡的雙渠道供應鏈協調問題,利用聯合契約來協調雙渠道供應鏈。

在基于市場需求和制造商產出不確定條件下,本文展開了基于CVaR 的雙渠道供應鏈庫存決策及協調方面的研究,分別構建了分散和集中情況下雙渠道供應鏈最優庫存決策模型。為解決和避免渠道沖突和雙重邊際效應,設計了結合回購和收益共享的聯合契約來進行雙渠道供應鏈的協調,分析了產需不確定因子、風險規避因子、市場分配比例及契約參數對雙渠道供應鏈庫存決策及利潤的影響,討論了聯合契約實現雙渠道供應鏈協調的帕累托改進范圍。最后,通過算例驗證了模型和聯合契約協調的有效性。

1 問題描述與研究假設

雙渠道供應鏈庫存決策及協調問題中所涉及的不確定性包括市場需求和制造商產出不確定性,以及由于市場需求不確定性導致的零售商風險規避特性。其中,制造商面臨著線上線下的渠道競爭和沖突。

1.1 問題定義與描述

風險規避零售商和風險中性制造商組成的雙渠道供應鏈如圖1所示,制造商在線上渠道銷售給顧客,在線下渠道銷售給零售商。各成員以自身利益最大化為目標。

顧客對線下產品的需求量為:Dr=θX-pr+βrpd,顧客對線上產品的需求量為:Dd=(1-θ)Xpd+βdpr。其中,θ為線下渠道的市場分配比例(0＜θ＜1),βi(i=r,d)為交叉價格影響系數(0＜βi＜1),X為市場總需求量,X∈[A,B](0≤A＜B),分布函數為F(x),概率密度函數為f(x),μ1 為需求不確定均值。零售商的訂購量為qr,制造商計劃產出量為qm,制造商實際產量為yqm,制造商庫存量為:Im=yqm-qr,y為非負隨機變量,y∈[C,D](0＜C＜D≤1),分布函數為G(y),概率密度函數為g(y),μ2為產出不確定均值。為了方便討論,做出如下假設:

(1)X為市場總需求量,是非負、連續的隨機變量,其分布函數F(x)和概率密度函數f(x)都為連續、可微的增函數。

(2)y為產出不確定因子,是非負、連續的隨機變量,其分布函數G(y)和g(y)都是連續、可微的。

(3)假設制造商的直銷價格大于其生產成本即pd＞cm,以確保制造商收益為正。

(4)制造商優先給零售商供貨,以確保雙渠道供應鏈的穩定性。

(5)產品的零售價大于批發價和零售商的銷售成本之和,即pr＞ω+cr,以確保零售商收益為正。

(6)雙渠道供應鏈中各成員是完全理性的,均以利潤最大化為目標進行決策。

(7)θX-pr＞0和(1-θ)X-pd＞0,以確保各渠道擁有各自的忠實顧客。

(8)制造商為風險中性,通過契約方式激勵零售商的購買行為,促使產品能夠為更多零售商購買。

1.2 符號與參數說明

pr——產品的零售價格

pd——產品的直銷價格

ω——單位產品的批發價格

vm——制造商剩余產品的殘值

vr——零售商剩余產品的殘值

b——制造商給零售商剩余產品單位回購價格

η——零售商風險規避系數

Dr——顧客對零售商的需求量

Dd——顧客對生產商的需求量

βr——直銷渠道對零售渠道的影響因子

βd——零售渠道對直銷渠道的影響因子

λ——收益共享因子

θ——雙渠道供應鏈零售渠道的市場分配比例

zr——零售商的庫存因子

zm——制造商的庫存因子

X——產品的市場總需求量

y——制造商的隨機產出因子,0≤y≤1

μ1——市場需求不確定均值

μ2——制造商產出不確定均值

qm——制造商的計劃產出量

qr——零售商的訂購量

cm——制造商的生產成本

cr——零售商的銷售成本

Im——制造商的庫存量

Πm——制造商的利潤

ΠT——供應鏈整體利潤

hr——零售商的庫存成本

hm——制造商的庫存成本

2 分散情況下雙渠道供應鏈最優庫存決策模型

在分散式雙渠道供應鏈下,制造商和零售商獨立決策,追求各自利潤最大化。本文研究的雙渠道供應鏈是以制造商為主導的Stackelberg博弈,即包括制造商確定批發價格和計劃產量以及零售商確定訂購量。決策順序可以描述為:制造商確定批發價格和計劃產量,零售商根據制造商的決策結果,確定自身的訂購量。本文采用逆向推導法,首先確定博弈的后序階段,如給定制造商的批發價格和計劃產量,零售商實現利潤最大化并確定最優的訂購量,然后確定博弈的前序階段,如制造商根據零售商的訂購量進行自身決策,即制造商確定最優批發價和計劃產量。

2.1 風險規避零售商最優庫存決策模型

CVaR 由Rockafellar等[29]提出并證明用于度量風險程度的方法。由于CVaR 度量了低于分位數η的平均值,主要考慮低于分位數的平均收益,并且具有次可加性,故CVaR 成為供應鏈風險決策問題中的常用工具。通常假設CVaR 的一般化定義公式:

式中:v表示隨機變量的η分位數;E為決策變量的期望值,且η∈(0,1]為決策者的風險規避系數,表示決策者的風險規避度,η越小,表示決策者風險規避度越大;Πr為零售商的利潤函數。

零售商的利潤函數表示為

當Dr≤qr時,第1項表示零售商的銷售收入,第2項表示殘值收入,第3項表示庫存成本,第4項表示采購成本,第5項表示銷售成本;當Dr＞qr時,第1項表示零售商的銷售收入,第2項表示采購成本,第3 項表示銷售成本。假設zr=(qr+prβrpd)/θ,將zr代入式(2),可得

風險規避零售商最大條件風險值為

式中,

定理1分散決策下,零售商的最優訂貨量和最優條件風險值分別為:

證明分3種情況討論最優解v*的取值:

(1)當

(2)當

時,其中:

(3)當v＞(pr-ω-cr)(θzr-pr+βrpd)時,

上述分析表明,v的最優解只能在半開半閉區間

內取得,分兩種情況討論:

(1)當F(zr)＞η時,

則在開區間

中,必存在某個v滿足1-(h1)=0,可得

得=θF-1(η)-pr+βrpd,這與F(zr)＞η矛盾。

(2)當F(zr)≤η時,

根據定理1,分別對式(6)、(7)求一階導數,可得推論1。

推論1分散決策下,供應鏈決策變量滿足如下關系:

由推論1分析可得,當零售商風險規避程度增大時,零售商的訂貨量減少,CVaR 值也隨之減小;當零售渠道的市場分配比例增大時,零售商的訂貨量增大;當直銷渠道對零售渠道的影響因子βr 增大時,即渠道競爭增強,零售商的訂貨量和CVaR 值也隨之增大。隨著線上直銷價格pd的增加,零售商訂貨量及CVaR 值均增加。由推論1可以看出,零售商可以根據風險規避程度、市場分配比例、直銷渠道對零售渠道的影響因子及線上直銷價格,調整自身的訂貨量,使自身的利潤最大化。

2.2 制造商最優庫存決策模型

制造商的利潤函數為

當Dd≤yqm-qr時,第1項表示制造商線上渠道的銷售收入,第2項表示殘值收入,第3項表示庫存成本,第4項表示線下渠道的銷售收入,第5項表示生產成本;當Dd＞yqm-qr時,第1項表示制造商線上渠道的銷售收入,第2項表示線下渠道的銷售收入,第3項表示生產成本。假設zm=(yqmqr+pd-βdpr)/(1-θ),將zm代入式(8),可得

制造商的期望利潤函數為

定理2分散決策下,存在唯一的(ωd*),使制造商的期望利潤最大化,且滿足如下條件:

定理2的證明詳見附錄。

推論2分散決策下,供應鏈決策變量滿足如下關系:

由推論2可以看出,當零售渠道的市場分配比例增大時,制造商庫存量及期望利潤減少;當零售渠道對直銷渠道的影響因子βd 增大時,制造商庫存量及期望利潤也隨之增大;當線下零售價格pr增大時,制造商庫存量及期望利潤均增大。由推論2還可以看出,制造商可通過對零售渠道的市場分配比例、零售渠道對直銷渠道的影響因子及線下零售價格調整自身的庫存量,使自身的利潤最大化。

3 集中情況下雙渠道供應鏈最優庫存決策模型

集中情況下,雙渠道供應鏈期望利潤函數為

定理3集中決策下,存在唯一的使雙渠道供應鏈的期望利潤最大化,且滿足如下條件:

定理3的證明詳見附錄。

推論3集中決策下,供應鏈決策變量滿足如下關系:

由推論3可知,集中決策下,當零售商風險規避程度增大時即η減小,零售商的訂購量減少,制造商的庫存量減少,供應鏈總利潤降低。當零售渠道市場分配比例θ增大時,零售商的訂購量增加,制造商的庫存量減少。當直銷渠道對零售渠道的影響因子βr增大時,即不同渠道間的競爭程度增大,零售商的訂購量增大,制造商的庫存量減少,雙渠道供應鏈的總利潤也隨之增大。當線下零售價格pr增大時,零售商訂購量及制造商庫存量均增大;當線上直銷價格pd增大時,雙渠道供應鏈的總利潤也呈上升趨勢。由推論3可以看出,在集中決策下,根據零售商風險規避程度、零售渠道市場分配比例、直銷渠道對零售渠道的影響因子、線下零售價格及線上直銷價格的控制,調整零售商和制造商的庫存量,從而使雙渠道供應鏈的總利潤達到最優。

4 基于聯合契約的雙渠道供應鏈庫存決策模型

本文設計了改進的回購契約及收益共享契約組成的聯合契約來協調雙渠道供應鏈庫存。當零售商的訂購量小于時,制造商回購全部剩余產品;當零售商的訂購量大于時,制造商按照α(0＜α＜1)的比例回購剩余產品,并且回購價小于批發價,規避了零售商過度訂購帶來的潛在風險。零售商將自己收益的1-λ共享給制造商。

聯合契約的協調順序為:①制造商作為供應鏈主導者確定契約(ω,λ,b);②制造商根據契約確定計劃產出量qm;③零售商根據制造商確定的契約確定訂購量qr;④制造商確定最終的契約形式。實現雙渠道供應鏈協調的聯合契約須滿足如下兩個條件:①使分散情況下雙渠道供應鏈的利潤達到集中情況下的利潤;②制造商的期望利潤和零售商的CVaR值分別高于分散決策水平,實現帕累托改進。

4.1 風險規避零售商的最優庫存決策模型

零售商的利潤函數表示為

當qr≤時,第1項表示零售商未共享的收益,第2項表示制造商回購產品使零售商得到的收益,第3項表示采購成本,第4項表示銷售成本;當qr＞時,第1項表示零售商未共享的收益,第2項表示庫存成本,第3項表示制造商按照α比例回收剩余產品使零售商得到的收益,第4項表示采購成本,第5項表示銷售成本。將zr代入式(17)并對其求CVaR,可得當zr≤時,

當zr＞時,

定理4聯合契約下,零售商的最優訂購量滿足如下條件:

定理4的證明詳見附錄。

4.2 制造商最優庫存決策模型

制造商的利潤函數表示為

式中:第1項表示制造商線上渠道的銷售收入,第2項表示殘值收入,第3項表示庫存成本,第4項表示線下渠道的銷售收入,第5項表示生產成本,第6項表示零售商分享給制造商的收益,第7項表示制造商回購零售商產品后所帶來的殘值收益回購成本及庫存成本。

式中:第1項表示制造商線上渠道的銷售收入,第2項表示殘值收入,第3項表示庫存成本,第4項表示線下渠道的銷售收入,第5項表示生產成本,第6項表示零售商分享給制造商的收益,第7項表示制造商按照α比例回購剩余產品所帶來的殘值收益回購成本及庫存成本。將zm代入式(21)、(22)并對其求期望,可得制造商的期望利潤函數。

當zr≤時,

定理5聯合契約下,制造商最優庫存量I*m滿足如下條件:

證明在式(23)、(24)中對qm求一階和二階偏導均可得:

定理6聯合契約實現雙渠道供應鏈協調,需滿足如下條件:

定理6的證明詳見附錄。

由定理6可知,當λ確定時,隨著η的增大,回購價增大;隨著η的減小,回購價減少。這說明了當收益共享因子不變時,零售商的風險規避程度和回購價成反比;零售商風險規避程度越大,回購價越小,反之亦成立。可見,在制定聯合契約時,制造商與零售商可通過調整收益共享因子、回購價以及批發價,使雙方協調后的利潤均大于分散情況下的利潤,從而達到雙贏的目標。

5 算例分析

本節通過算例驗證模型和聯合契約的有效性。假設市場需求X服從[0,800]的均勻分布,制造商隨機產出因子y服從[0.6,1]的均勻分布。其他參數為:pr=22,pd=20,cm=6,cr=1,hr=2,hm=2,vm=5,vr=5,βr=0.75,βd=0.75。

5.1 零售商風險規避下雙渠道供應鏈庫存決策分析

通過計算可得出分散和集中情況下的雙渠道供應鏈最優決策及期望利潤值,如表1所示。由表1可看出,零售商最優訂購量、制造商庫存量及供應鏈整體利潤小于集中決策的相應結果。隨著零售商風險規避程度的增加,零售商訂購量、制造商庫存量及批發價均減少,零售商的CVaR 值和制造商的期望利潤隨之減少。

表1 不同風險規避程度下分散和集中的最優決策

圖2所示為分散決策下,需求不確定均值μ1和風險規避系數η對零售商庫存因子zr的影響。由圖2可見,當η不變時,隨著μ1的增大,零售商庫存因子增大即應對線下不確定的需求而訂購的量增大。當μ1 不變時,隨著η的增大,零售商庫存因子增大。

圖3所示為分散決策下,產出不確定均值μ2和風險規避系數η對制造商庫存因子zm的影響。由圖3可見,當η不變時,隨著μ2的增大,制造商庫存因子增大即制造商應對不確定性而為線上顧客準備的量增大。當μ2不變時,隨著η的增大,制造商庫存因子減少。

圖4所示為分散決策下,需求不確定均值μ1和風險規避系數η對零售商條件風險值CVaR(Πr)的影響。由圖4可見,當η不變時,隨著μ1 的增大,零售商的CVaR值增大。當μ1不變時,隨著η的增大,零售商的CVaR 值增大。

圖5、6分別所示為集中和分散決策下,線下零售價格pr和線上直銷價格pd對零售商及制造商期望利潤的影響。由圖5可見,當線下零售價格pr增大時,零售商的CVaR值、制造商期望利潤及供應鏈整體利潤均呈上升趨勢,且集中決策下供應鏈整體利潤高于分散決策下的值。由圖6可見,隨著線上直銷價格pd增大,零售商的CVaR 值、制造商期望利潤及供應鏈整體利潤均增加,且集中情況下供應鏈整體利潤高于分散情況下的值。

5.2 零售商風險規避下雙渠道供應鏈聯合契約協調分析

通過計算得出,聯合契約可以實現零售商風險規避下的雙渠道供應鏈庫存協調。其中,隨著收益共享因子和風險規避系數的增大,零售商和制造商的利潤增量均得到增加。圖7、8分別所示為市場分配比例θ在不同情況下,基于風險規避系數η的聯合契約帕累托改進區域。

由圖7 可見,在不同η下存在ΔCVaR(Πr)、ΔE(Πm)和基準線圍成的三角形區域即帕累托區域。隨著η的增大,帕累托改進區域增大,雙渠道供應鏈的利潤增量增大。隨著η的減小,帕累托改進區域減小,雙渠道供應鏈的利潤增量減小。隨著λ的增大,ΔCVaR(Πr)增大,ΔE(Πm)減少。由圖8可見,當θ不變時,η越大,帕累托改進區域越大。當η不變時,θ越大,帕累托改進區域越大。由圖7、8可見,當θ越大、η越大時,帕累托改進區域越大,聯合契約實現雙渠道供應鏈庫存協調的可能性越大。

表2所示為聯合契約下風險規避系數η和市場分配比例θ對帕累托改進區域的影響。由表2 可見,當風險規避系數η一定時,市場分配比例θ越大,帕累托改進區域越大。當市場分配比例θ一定時,風險規避系數η越大,帕累托改進區域越大。

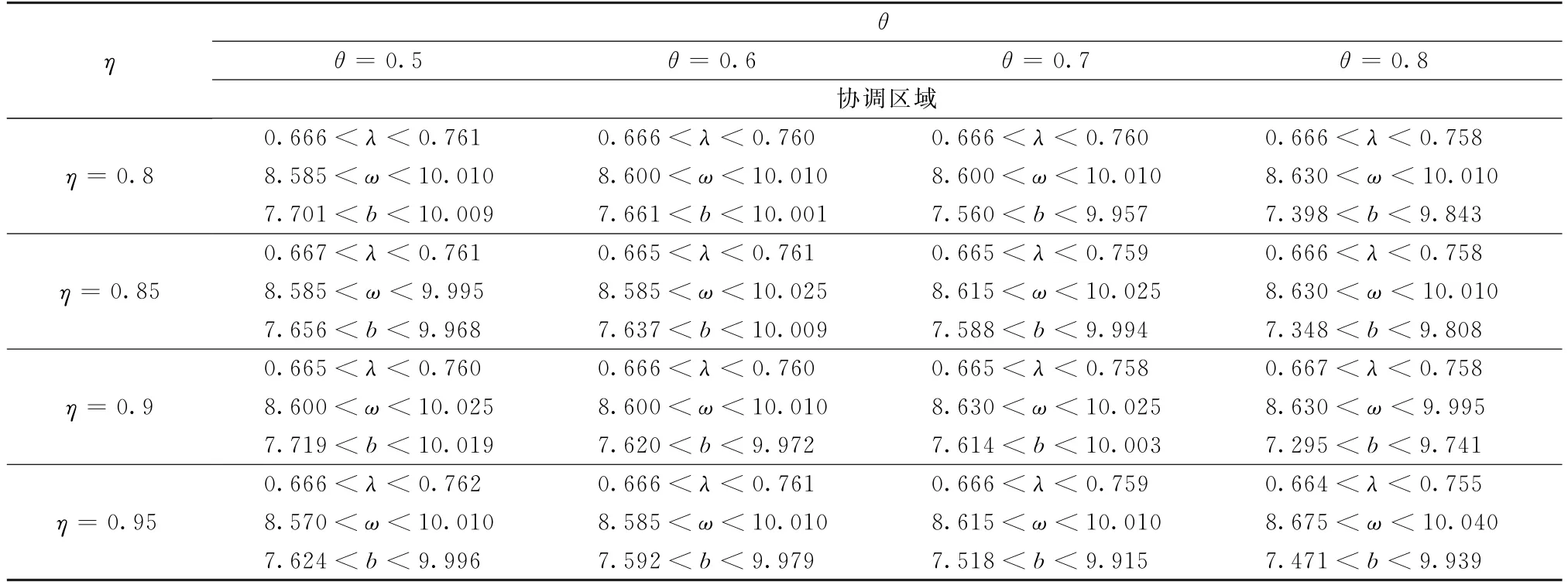
表2 θ 和η 對應下的帕累托改進區域

通過上述數值分析可以發現:

(1)當零售商風險規避系數增大時,零售商的訂購量、零售商庫存因子、批發價及條件風險值增大,制造商的庫存量及期望利潤增加,制造商庫存因子減少;當市場需求不確定因子增大時,零售商訂購量、零售商庫存因子及條件風險值增大。隨著產出不確定因子增加,制造商的庫存量減少,制造商庫存因子及期望利潤增加。

(2)隨著線下零售價格的增加,零售商條件風險值、制造商期望利潤及供應鏈總利潤均增加,集中決策下的結果高于分散決策下的結果。

(3)隨著線上直銷價格的增加,零售商條件風險值、制造商期望利潤及供應鏈總利潤均增加,集中情況下的結果高于分散情況下的結果。

(4)通過聯合契約進行協調時,當收益共享因子不變,隨著風險規避系數的增大,回購價格、零售商及制造商的利潤增量均增大;當風險規避系數不變,隨著收益共享因子的增大,批發價格、回購價格及零售商的利潤增量均減少,而制造商的利潤增量增大。

(5)聯合契約可以實現產需不確定下零售商風險規避的雙渠道供應鏈庫存協調。當市場分配比例和風險規避系數增大時,帕累托改進區域變大,即聯合契約實現雙渠道供應鏈庫存協調的可能性變大。

6 結論

本文研究了零售商風險規避下基于聯合契約的雙渠道供應鏈庫存決策問題,構建了零售商風險規避下雙渠道供應鏈最優庫存決策模型,證明了聯合契約實現風險規避下雙渠道供應鏈庫存協調的可能性。最后,通過算例驗證了庫存決策模型和契約協調的有效性。

基于上述研究得到如下管理啟示:

(1)零售商進行庫存決策時,通過訂購量調整,可以降低自身的風險規避程度,這樣雖然增加了庫存成本,但鼓勵了顧客消費并且增加了自身利潤,制造商的利潤也得到提高。另外,通過線上直銷價格和線下價格的調整可以實現自身利潤的增加。

(2)在制定相應的營銷策略時,制造商和零售商可以通過折扣、促銷活動或購物節等方式挖掘各自渠道的潛在顧客,提高各自渠道的市場分配比例,從而增加各自的利潤。

(3)制造商在制定相應的庫存策略時,可以根據零售商的風險程度進行調整,如面對風險規避程度較高的零售商時,制造商可以減少產量,避免自身利益受損,制造商通過降低自身的產出不確定性,實現庫存減少和期望利潤的增加。另外,制造商可以根據線上直銷價格和線下價格調整庫存策略,實現自身利潤的增加。

(4)制造商針對風險規避較高的零售商,可以采取回購契約方式鼓勵零售商增加訂貨,降低零售商風險規避程度。雖然制造商庫存成本有一定的增加,但制造商和零售商利潤均得到增加。

(5)制造商根據零售商的風險規避程度,通過回購和利潤共享實現雙渠道供應鏈庫存協調,最終達到“雙贏”的目標。

(6)制造商作為供應鏈的主導者,需要將契約規則置于合理范圍之內,否則將導致各自的利益受損以及合作降低。總之,通過降低風險規避程度和提高市場分配比例可以提高雙渠道供應鏈的利潤。

本文僅研究了不確定環境下單一風險規避的雙渠道供應鏈庫存協調問題,具有一定的局限性。針對多風險多渠道的供應鏈庫存協調問題將有待于進一步研究。

附錄

定理2的證明對式(6)求一階導數,可得式(13),即=K＜0。

將代入式(10),然后分別對ω和qm求一階和二階偏導,可得:

可得海賽矩陣:

并且?2E(Πm)/?ω2＜0。

通過分析可知海賽矩陣負定,存在唯一的(ωd*),使得制造商利潤最大,由于,故存在唯一的(ωd*),使制造商利潤最大。由一階偏導數等于零可得定理2。

定理3的證明在式(14)中分別對qr和qm求一階和二階偏導,可得:

可得海賽矩陣:

并且?2E(ΠT)/＜0。

定理4的證明對式(18)、(19)中qr求一階和二階偏導,可得:

當zr≤時,

當zr＞時,

由二階偏導均小于零可知兩階段均存在唯一的,使零售商的CVaR 值最大。由一階偏導為零可得式(20),定理4得證。

定理6的證明實現雙渠道供應鏈協調,須滿足。聯立式(15)、(20),如下式所示:

可得式(26),定理6得證。