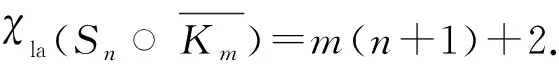圖的corona積的局部反魔幻著色數(shù)

楊 雪,邊 紅*,于海征, 丁吉麗

(1.新疆師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，新疆 烏魯木齊 830017;2.新疆大學(xué)數(shù)學(xué)與系統(tǒng)科學(xué)學(xué)院，新疆 烏魯木齊 830046)

1 預(yù)備知識(shí)

令G=(V(G),E(G))是一個(gè)沒有孤立點(diǎn)的有限簡(jiǎn)單無向圖.稱一個(gè)雙射f:E(G)→{1，2，…，|E(G)|}為圖G的反魔幻標(biāo)號(hào)，如果f滿足對(duì)于圖G的任意兩個(gè)頂點(diǎn)u和v都有w(u)≠w(v)，其中w(u)=∑e∈E(u)f(e)，E(u)是與頂點(diǎn)u相關(guān)聯(lián)的邊的集合.一個(gè)圖G稱為反魔幻的，如果圖G有一個(gè)反魔幻標(biāo)號(hào).

圖的反魔幻標(biāo)號(hào)的定義是由Hartsfield等[1]在1994年提出的， 他們還提出“除了K2以外的所有連通簡(jiǎn)單圖都有一個(gè)反魔幻標(biāo)號(hào)”的猜想，但至今這個(gè)猜想尚未完全解決.

近幾年，Arumugam等[2]和Bensmail等[3]分別獨(dú)立地提出了一個(gè)比反魔幻標(biāo)號(hào)相對(duì)較弱的定義：局部反魔幻標(biāo)號(hào)，并且也都提出“除了K2以外的所有連通簡(jiǎn)單圖都有一個(gè)局部反魔幻標(biāo)號(hào)”的猜想.這個(gè)猜想已由Haslegrave[4]得到完全解決.稱一個(gè)雙射f:E(G)→{1，2，…，|E(G)|}是圖G的一個(gè)局部反魔幻標(biāo)號(hào)，如果對(duì)于圖G的任何兩個(gè)相鄰的頂點(diǎn)u和v都有w(u)≠w(v)，其中w(u)=∑e∈E(u)f(e)，E(u)是與點(diǎn)u相關(guān)聯(lián)的邊的集合.一個(gè)圖G稱為局部反魔幻的，如果圖G有一個(gè)局部反魔幻標(biāo)號(hào).若對(duì)圖G的點(diǎn)v著顏色w(v),顯然圖G的任一個(gè)局部反魔幻標(biāo)號(hào)自然地導(dǎo)出圖G的一個(gè)正常點(diǎn)著色.同時(shí)Arumugam等[2]提出了局部反魔幻著色數(shù)的定義：圖G的局部反魔幻著色數(shù)是其局部反魔幻標(biāo)號(hào)中所使用的最少顏色數(shù)，記為χla(G)，他們還給出了路、圈、友誼圖、輪圖等一些特殊圖類的局部反魔幻著色數(shù)的確切值.

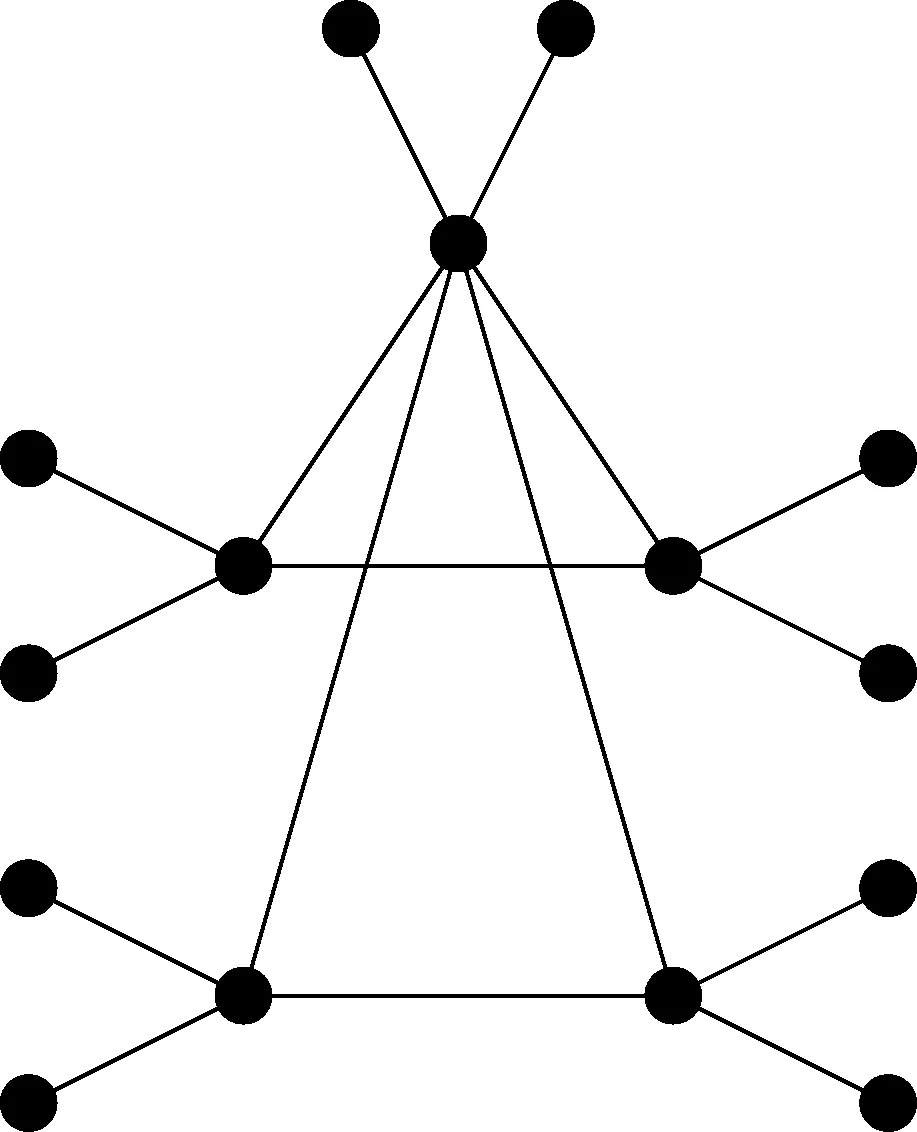
圖1 圖

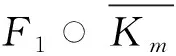
2.1 圖Fn○K1的局部反魔幻著色數(shù)

友誼圖Fn的頂點(diǎn)集V(Fn)={v1，v2，…，v2n，v2n+1}，其中v2n+1是友誼圖Fn中的n個(gè)三角形的公共頂點(diǎn)；邊集E(Fn)={vivi+1：1≤i≤2n,i是奇數(shù)}∪{v2n+1vi：1≤i≤2n}.圖Fn○K1中K1的2n+1個(gè)拷貝點(diǎn)記為{d1，d2，…，d2n,d2n+1}，如圖2所示.

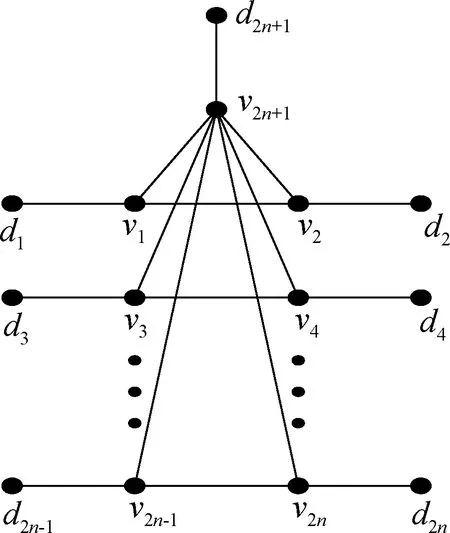
圖2 圖Fn○K1Fig.2Graph Fn○K1

下面的引理1和引理2分別給出了圖Fn○K1的局部反魔幻著色數(shù)的上、下界，由此可以得到圖Fn○K1的局部反魔幻著色數(shù)的確切值.

證明令f(e)表示圖Fn○K1中邊e上的局部反魔幻標(biāo)號(hào).對(duì)于圖Fn○K1的邊{v2n+1vi：1≤i≤2n}和邊{vivi+1:i是奇數(shù)}，給出如下標(biāo)號(hào):

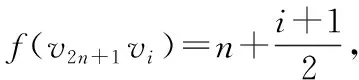
f(v2n+1vi)=4n+2-i,當(dāng)1≤i≤2n且i是偶數(shù)時(shí)；

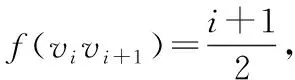
對(duì)于邊{vidi:1≤i≤2n},給如下標(biāo)號(hào):

最后，令f(v2n+1d2n+1)=5n+1.對(duì)于1≤i≤2n,根據(jù)i的奇偶性，對(duì)圖Fn○K1中的點(diǎn)vi的標(biāo)號(hào)和w(vi)(即點(diǎn)vi所著顏色)進(jìn)行分類討論.

當(dāng)i是奇數(shù)且i≠2n+1時(shí)，點(diǎn)vi所著顏色

w(vi)=5n+1，

當(dāng)i是偶數(shù)時(shí)，點(diǎn)vi所著顏色是

w(vi)=8n+2，

而點(diǎn)v2n+1所著顏色是

易知這3類點(diǎn)所著顏色互不相同.而圖Fn○K1中的點(diǎn)dj(1≤j≤2n+1)所著顏色顯然互不相同，故這2n+1個(gè)點(diǎn)共著了2n+1個(gè)不同顏色.點(diǎn)d2n+1所著顏色是

w(d2n+1)=5n+1,

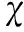
若對(duì)中心點(diǎn)v2n+1相關(guān)聯(lián)的邊使用最小標(biāo)號(hào)，有

w(v2n+1)=1+2+…+2n+1>5n+1≥w(dj)，

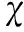
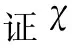
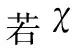
根據(jù)引理1和引理2可以得到圖Fn○K1的局部反魔幻著色數(shù)的確切值，有

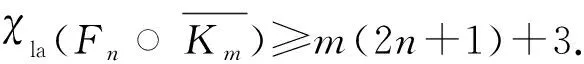
若對(duì)中心點(diǎn)相關(guān)聯(lián)的邊使用最小標(biāo)號(hào)，有

w(v2n+1)=1+2+…+2n+m>m(2n+1)+3n,

而任意一個(gè)懸掛點(diǎn)dj所著顏色

w(dj)≤m(2n+1)+3n,(1≤j≤m(2n+1)),

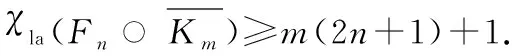
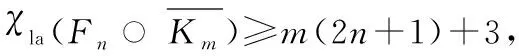
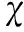
即可，其中a∈{1，2}.

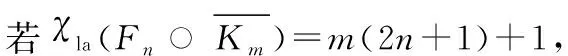
w(vi)=w(dj)≤m(2n+1)+3n,i≠j, 1≤i≤

2n, 1≤j≤m(2n+1).

顯然與這2n個(gè)頂點(diǎn)不相關(guān)聯(lián)的邊有m條，則與這2n個(gè)頂點(diǎn)相關(guān)聯(lián)的邊有2mn+3n條.令這2n個(gè)頂點(diǎn)的著色總和為σ,則有

σ≤2n[m(2n+1)+3n].

此外，若對(duì)與這2n個(gè)點(diǎn)相關(guān)聯(lián)的2mn+3n條邊使用最小的標(biāo)號(hào)，有

σ≥1+2+…+(2mn+3n),

故

2n[m(2n+1)+3n]≥1+2+…+(2mn+3n).

又因?yàn)?/p>

1+2+…+(2mn+3n)-2n[m(2n+1)+3n]=

4m2n2+4mn2-3n2-2mn+3n>0,

這與2n[m(2n+1)+3n]≥1+2+…+(2mn+3n)是矛盾的.

σ≤k[m(2n+1)+3n].

此外,若與這k個(gè)點(diǎn)相關(guān)聯(lián)的n+(m+1)k條邊使用最小標(biāo)號(hào)，則

a≥1+2+…+n+(m+1)k.

故

1+2+…+n+(m+1)k≤k[m(2n+1)+3n].

而

1+2+…+n+(m+1)k-k[m(2n+1)+3n]=

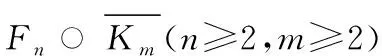
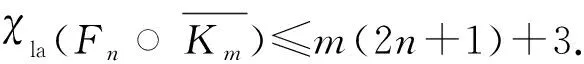
1≤j≤m}.

w(vi)=5n+1，

當(dāng)i是偶數(shù)時(shí)，點(diǎn)vi相關(guān)聯(lián)的部分邊標(biāo)號(hào)和是

w(vi)=8n+2,

點(diǎn)v2n+1相關(guān)聯(lián)的部分邊標(biāo)號(hào)和是

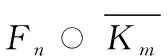
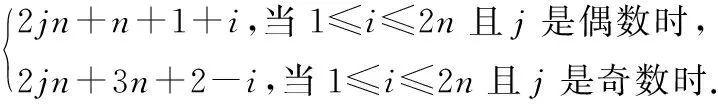
通過計(jì)算可知：當(dāng)i是奇數(shù)且i≠2n+1時(shí)，點(diǎn)vi著顏色

當(dāng)i是偶數(shù)時(shí)，點(diǎn)vi著顏色

點(diǎn)v2n+1著顏色

因此得到了3個(gè)互異的顏色且這3個(gè)顏色不同于懸掛點(diǎn)著的顏色，得證.

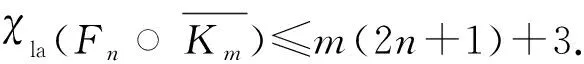
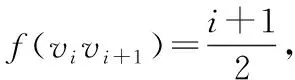
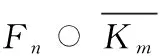
通過計(jì)算可得：當(dāng)i是奇數(shù)且i≠2n+1時(shí)，點(diǎn)vi所著顏色是

當(dāng)i是偶數(shù)時(shí)，點(diǎn)vi所著顏色是

點(diǎn)v2n+1所著顏色是

由此得到3種互異的顏色且這3種顏色不同于懸掛點(diǎn)所著顏色，得證.

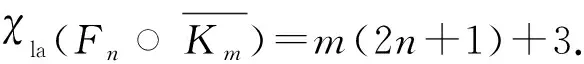
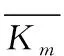
m},

n,1≤j≤m}.

本節(jié)將根據(jù)星圖Sn的頂點(diǎn)個(gè)數(shù)給出圖Sn○K1的局部反魔幻著色數(shù)的確切值.

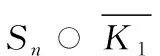
n}.

圖3 圖Sn○K1Fig.3Graph Sn○K1

當(dāng)n≥2時(shí)，圖Sn○K1有n+1個(gè)葉子點(diǎn)，則由定理3易知圖Sn○K1的局部反魔幻著色數(shù)的下界.

下面給出圖Sn○K1的局部反魔幻著色數(shù)的上界.

證明根據(jù)圖Sn○K1中邊的分布情況，將邊如下標(biāo)號(hào)(其中1≤i≤n,x為中心點(diǎn))：

f(xui)=i,

f(xd1)=2n+1.

可以得到

w(ui)=2n+1,

w(d1)=2n+1,

根據(jù)引理6和引理7,可以得到圖Sn○K1的局部反魔幻著色數(shù)的確切值.

m},

n,1≤j≤m}.

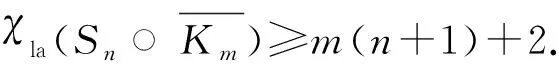
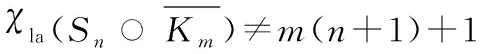
即可.

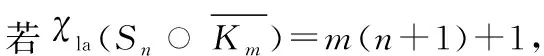
w(x)=1+2+…+n+m>m(n+1)+n,

而每個(gè)懸掛點(diǎn)所著顏色都不超過m(n+1)+n,所以剩余的n個(gè)點(diǎn)必定與某些懸掛點(diǎn)著相同顏色.

與點(diǎn)ui(1≤i≤n)相關(guān)聯(lián)的邊有n(m+1)條.令σ為這剩余的n個(gè)點(diǎn)所著顏色的總和.若對(duì)與這n個(gè)點(diǎn)相關(guān)聯(lián)的邊用最小標(biāo)號(hào)，則有

σ≥1+2+…+n(m+1).

另一方面，每個(gè)點(diǎn)ui(1≤i≤n)所著顏色必與某個(gè)懸掛點(diǎn)所著顏色相同，而每個(gè)懸掛點(diǎn)所著顏色都不超過m(n+1)+n,則有

σ≤n[m(n+1)+n].

故

n[m(n+1)+n]≥1+2+…+n(m+1).

事實(shí)上，

[1+2+…+n(m+1)]-n[m(n+1)+n]=

m2n+1>0,

因此，n[m(n+1)+n]≥1+2+…+n(m+1)是不可能的，矛盾.

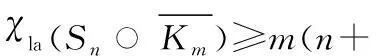
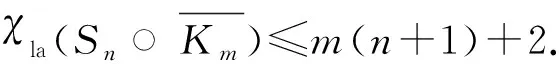
m},

n,1≤j≤m}.

f(xui)=i,

f(xd1)=2n+1.

f(xdj)=mn+n+j,當(dāng)j≠1時(shí).

綜上可得，當(dāng)1≤i≤n時(shí)，ui所著顏色

中心點(diǎn)x所著顏色

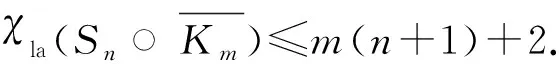
f(xdj)=2n+j.

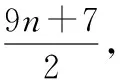
f(xdj)=nm+n+j,當(dāng)3≤j≤m時(shí).

綜上可知，點(diǎn)ui所著顏色

點(diǎn)x所著顏色

容易看出這是兩個(gè)互異的顏色，且不同于懸掛點(diǎn)所著的顏色，得證.

f(xd1)=n+1,

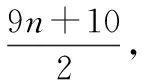
f(xdj)=nm+n+j,當(dāng)3≤j≤m時(shí).

綜上可知，點(diǎn)ui所著顏色

點(diǎn)x所著顏色

容易看出這是兩個(gè)互異的顏色，且不同于懸掛點(diǎn)著的顏色，得證.