考慮隨機外強迫的濕大氣方程組弱解的適定性分析

張博冉，連汝續

(華北水利水電大學數學與統計學院，河南 鄭州 450046)

1 預備知識

本文研究了曾慶存院士[1]提出的濕大氣動力學方程組，證明了隨機外強迫作用下濕大氣動力學方程組初邊值問題整體弱解的存在性和穩定性. 下面首先介紹濕大氣方程組的初邊值問題. 引入地形坐標系(θ,λ,ζ;t)，θ是余緯且θ∈[0,π]，λ是經度且λ∈[0,2π]，p是氣壓且p∈[0,ps]，ps為地表處氣壓，ζ=p/ps∈[0,1]，t表示時間. 那么，考慮如下隨機外強迫作用的濕大氣方程組.

大氣運動方程：

(1)

大氣熱力學方程：

(2)

水汽方程：

(3)

連續性方程：

(4)

準靜力平衡方程：

(5)

其中，Co,Cp,R是熱力學常數，ui,vi(i=1,2,3)是耗散系數，g是重力加速度，w是地球自轉角速度，Ψ1表示單位時間內大氣從外界獲得的熱量，Ψ2表示水汽相變過程中液態水的變化量.

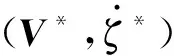
參考文獻[3-4]中的方法，可給出隨機外強迫的定義.在完備的概率空間(Ω,F,P)中，假設ω1,ω2,ω3,…是樣本空間Ω中一列期望為E的獨立標準的布朗運動，隨機過程W是一個wiener過程，因此隨機外強迫Ψ可定義如下：

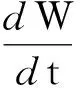
(6)

是關于時間的加性白噪聲，而G是從(L2(Ω))2到(H1+2γ0(Ω))2(γ0>0)的Hilbert-Schmidt算子.假設

(7)

是滿足以下隨機Stokes方程初值問題

(8)

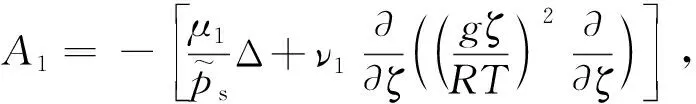
定義Ψ1為非絕熱加熱作用，Ψ2為水汽相變作用. 其余參數的含義可參見文獻[1-2].

接下來，定義系統(1)～(5)的初邊值條件. 首先，給定初值條件為

V|t=0=V0,T|t=0=T0,q|t=0=q0,

(9)

再給出邊界條件為

(10)

目前大氣動力學方程組的適定性問題已經取得了很多重要成果. 例如，曾慶存[5]就曾系統地論述過多種大氣模式解的適定性，并提出了海氣耦合問題. 隨后，文獻[2,6-15]研究了基于原始方程的各種大氣動力學方程組，并證明了方程組初邊值問題整體弱解和強解的適定性.另外文獻[16-20]還研究了考慮水汽相變過程的濕大氣方程組初邊值問題的適定性.關于研究大氣方程組吸引子的結論，可參見文獻[11-12,14-17,21-22].

目前對考慮隨機因素的大氣方程組也有一些重要的結論. 例如，文獻[23-25]中建立了隨機氣候模式和考慮隨機外強迫作用的海氣耦合模式. 之后，Griffies等[26]和Majda等[27-30]又對考慮隨機外強迫作用的氣候模式進行了數學理論和數值計算方面的研究.郭柏靈等[3-4]還研究了考慮隨機外強迫作用的海洋原始方程組的適定性以及整體吸引子的存在性等. 2018年，Dong等[31]研究了具有指數混合性質的三維隨機原始方程的適定性，得到了所有的弱解都有同一個不變測度，以及強解不變測度的唯一性.

2 主要結論

首先，利用式(4)和(5)，結合邊界條件，可將考慮隨機外強迫作用的濕大氣動力學方程組簡化為如下形式：

(11)

定義未知函數U∶=(V,T′,q)，進而給定初值為

U0,

邊界條件為

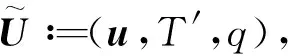
(12)

系統(12)滿足如下邊界條件：

(13)

接下來定義如下算子：

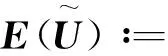
下面可給出類似于文獻[2]中弱解的定義.

下面給出整體弱解的存在性和穩定性定理.

注：借鑒參考文獻[2]中注2.2的方法，利用葉果洛夫定理可證明整體弱解的幾乎處處穩定性，這里省略了具體的證明過程.

3 能量估計

本部分給出系統(12)～(13)的能量估計.

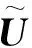
(14)

這里C(M)是與時間M有關的常數.

證明令式(12) 與(u,T′,q)作內積，并利用邊界條件得

q2]|ζ=1dσ=I1+I2+I3+I4+I5+

其中

由H?lder不等式和Young不等式可得

|I1|≤C‖Z‖L2(Ω)‖T′‖L2(Ω)+

(15)

這里C表示某正常數，下同. 又因為

(16)

且有

本文利用復模態指示函數法和多參考點最小二乘復頻域法對測量所得汽車發動機飛輪頻響函數矩陣進行分析，然后再對結果進行了二級驗證。運用OROS V3動態信號分析儀、NVGATE和Modal II分析軟件，采用多參考點錘擊技術對飛輪進行動態性能測試，獲得試驗模態參數。利用Solidworks與ANSYS軟件建立飛輪模型并計算出了理論模態參數。結果顯示，二者的固有頻率接近、振型相似，驗證了發動機飛輪模型的準確性。本研究對改進發動機飛輪結構，促使汽車輕量化具有一定的參考價值。

(17)

又由H?lder不等式、插值不等式和Young不等式可得

(18)

這里ε是任意小的常數，下同. 另外由H?lder不等式、Minkowski不等式、插值不等式和Young不等式可得

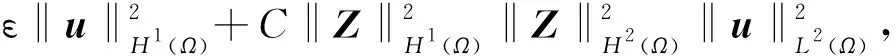
(19)

同理可得

(20)

(21)

綜合式(16)～(21) 可得

由分部積分可得I3=0,I4=0, 進一步由H?lder不等式和Young不等式可得

綜上可得

對上式使用Gronwall不等式，即可證明式(14)成立.

4 定理證明

(22)

和

0,

(23)

其中

在下面的證明過程中，對于不含Z的項，可利用類似參考文獻[2]中引理4.2的證明方法得到，這里略去具體證明過程. 那么首先給出J1的先驗估計

C‖u*k‖H1(Ω)‖Z‖H1(Ω)‖φ1‖H1(Ω)≤

同理可得

其中，由分部積分、H?lder不等式、Minkowski不等式和插值不等式可得

(‖φ‖L6(Ω)+‖φζ‖L6(Ω))≤

同理可得

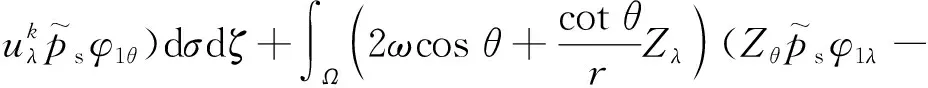
其中，由H?lder不等式可得

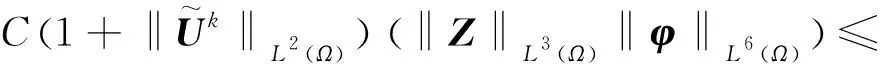
C.

最后，由Hardy不等式和H?lder不等式可得

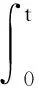
利用上述結論和參考文獻[2]引理4.2的證明方法可得

F∈L2(0,M;H-2(Ω)),

再借鑒文獻[11-12]的證明思路，可得到系統(12)～(13)整體弱解的存在性，即定理2.1成立，這里不再給出具體證明過程.

接下來，證明系統(12)～(13) 整體弱解的穩定性.

采用類似文獻[2]第4章的證明方法，當m→+∞，可得以下緊性框架：

5 結 論