Pythagorean模糊對稱交叉熵及加權投影的多屬性決策

韓二東，李占強

洛陽師范學院 商學院，河南 洛陽 471934

為打破直覺模糊集中專家對于方案在各屬性下的隸屬度和非隸屬度的和不能超過1的約束，Yager等[1]推廣了直覺模糊集，提出了能夠描述隸屬度和非隸屬度之和超過1，而兩者的平方和不超1的Pythagorean模糊集，從而更為精確地描述專家對各方案關于各屬性的評價偏好，不僅比直覺模糊集表達的模糊現象范圍更廣、刻畫和表達模糊信息的能力更強，而且提高了多屬性決策應用的靈活性[2]。

自提出Pythagorean模糊集以來，基于Pythagorean模糊集以及各類型擴展形式的決策理論與方法受到學者們的廣泛關注，相關研究主要分為3大類，首先是對其運算法則、得分函數、精確函數、信息測度等基礎理論的研究，Zhang等[3]定義了Pythagorean模糊集的加法、乘法、數乘和冪運算，給出其得分函數與相互比較的基本方法，并提出了Pythagorean模糊集的相似測度；Gou等[4]研究了Pythagorean模糊集的連續性和可導性；劉衛鋒等[5]考慮到隸屬度和非隸屬度之間可能存在的交叉影響，重新定義Pythagorean模糊數的運算法則，使得相關運算結果更為穩健，也更加符合常理；文獻[6]針對基于代數積和代數和運算法則的局限性，定義了Pythagorean模糊Hamacher運算，并研究運算的相關性質；李德清等[7]研究了Pythagorean模糊集的距離測度；Garg[8]定義了Pythagorean模糊集的信息能量、相關指標及相關系數，并與已有的其他類型模糊集相關系數進行比較分析；劉衛鋒等[9]受此啟發，在定義Pythagorean猶豫模糊集的信息能量、相關指標的基礎上，提出Pythagorean猶豫模糊集的相關系數及加權相關系數，從專家對不同方案評價的整體視角得到各方案的優劣次序，凸顯Pythagorean猶豫模糊集表達決策者猶豫不決偏好信息的顯著優勢；此外，文獻[10]定義了Pythagorean模糊集的熵和包含測度。

其次是Pythagorean模糊信息集成算子及其決策應用研究。Yager[11]提出了Pythagorean模糊加權平均算子（PFWA）和有序加權平均算子（PFOWG）；考慮到隸屬度和非隸屬度之間的關聯和相互影響[5]，提出了Pythagorean模糊交叉影響加權平均算子（PFIWA）、交叉影響有序加權平均算子（PFIOWA）、交叉影響幾何平均算子（PFIWG）及交叉影響有序加權幾何平均算子（PFIOWG），并給出各算子的具體計算公式；針對屬性間存在相互關聯的多屬性決策問題，彭定洪等[12]提出了Pythagorean模糊Heronian算子及加權算子，并討論算子的性質；Garg[13]定義Pythagorean模糊Einstein運算下的一系列算子；考慮到Hamacher t-模和t-余模既是對代數積和代數和的推廣，也是對Einstein積和Einstein和的推廣，將Hamacher積和Hamacher和拓展到Pythagorean模糊環境[6]，定義了Pythagorean模糊Hamacher加權平均算子（PFHWA）、Hamacher有序加權平均算子（PFHOWA）、Hamacher加權幾何算子（PFHWG）、Hamacher有序加權幾何算子（PFHOWG）；常娟等[14]考慮各屬性信息分布的疏密程度，提出Pythagorean密度集成算子；還涉及到Pythagorean模糊冪平均算子[15]、Pythagorean模糊冪Bonferroni集成算子[16]、Pythagorean模糊Choquet積分算子[17]、對稱Pythagorean模糊加權平均算子[18]、Pythagorean模糊BM算子[19]、廣義Pythagorean模糊算子等[20]算子，能夠用于解決屬性關聯的多屬性決策問題。此外，將Pythagorean模糊集與其他類型的模糊集結合，針對其拓展形式提出了一系列的信息集成算子，例如，Zhang[21]和Peng等[22]提出Pythagorean區間模糊集，并將QUALIFLEX方法應用于解決Pythagorean區間模糊多屬性群決策問題；將Pythagorean模糊集由離散集合拓展到連續集合，杜玉琴等[23]探討了基于Pythagorean三角模糊語言的Hamacher集成算子；范建平等[24]提出三角Pythagorean模糊集并研究了相關算子及性質；Khan等[25]將優先級平均算子（PA）與Pythagorean模糊集結合，提出了Pythagorean模糊優先級集結算子，隨后翟運開等[26]定義猶豫Pythagorean模糊語言優先級集結算子，并由此構建解決屬性間存在優先級關系的多屬性決策方法；彭新東等[27]定義了Pythagorean模糊語言集和Pythagorean模糊軟集，隨后文獻[28]在定義Pythagorean猶豫模糊語言集的基礎上，提出相應的加權平均算子、加權幾何算子及有序算子；李鵬等[29]基于Heronian算子提出Pythagorean模糊不確定語言加權Heronian平均算子（PFULWHM）和Pythagorean模糊不確定語言加權幾何Heronian平均算子（PFULWGHM）。

第三是將傳統多屬性決策方法拓展到Pythagorean模糊環境，提出基于Pythagorean模糊評價的多屬性決策方法。Zhang等[3]提出Pythagorean模糊TOPSIS法；Chen[30]構建Pythagorean模糊VIKOR法；Liang等[31]提出基于理想解的Pythagorean模糊三支決策方法；李美娟等[32]提出一種基于新得分函數和累積前景理論的Pythagorean模糊TOPSIS法；后續研究還涉及到Pythagorean模糊QUALIFLEX法[33]、基于信息熵的Pythagorean模糊LINMAP法[34]、帶有可能度的區間Pythagorean模糊決策方法[35]、基于前景理論的Pythagorean模糊TODIM法[36]、基于前景理論和新距離測度的Pythagorean模糊決策方法[37]、基于前景理論的Pythagorean猶豫模糊不確定語言ELECTRE決策方法[38]、Pythagorean模糊投影法等[39]；李娜等[40]定義區間Pythagorean模糊數的相對熵并提出一種基于相對熵的AQM多屬性決策方法，并考慮決策者的后悔規避和失望規避心理行為，基于構建的Pythagorean模糊熵提出風險型多屬性決策方法。所提出的多種類型多屬性決策方法已應用于投資決策、風險評估、醫療診斷、綠色供應商選擇、人力資源選拔推薦等領域，取得了良好決策效果。

綜上所述，當前關于Pythagorean模糊集決策理論與方法的研究取得了較為顯著的研究成果。其中，關于算子理論及應用的研究，一類是在屬性間相互獨立、互不關聯的假設前提下，提出基于Pythagorean模糊集的加權平均算子、加權幾何算子、有序算子、廣義算子或混合型算子，證明了各類算子的具體表達式，并詳細討論各算子的置換不變性、冪等性、單調性、有界性等性質，提出相應的多屬性決策方法；另一類是針對屬性間存在冗余、互補、偏好關系等關聯性的多屬性決策問題，將Choquet積分、Heronian平均算子、冪Bonferroni平均算子、Hamacher平均算子等擴展到Pythagorean模糊環境，提出了一系列信息集成算子及多屬性決策方法，部分算子具有較強的一般性，通過討論算子所含參數取值的變化對方案排序結果的影響進行靈敏度分析和對比分析，從而驗證決策方法的有效性與可行性，參數取值變化體現出決策者的風險偏好或主觀態度，此類算子具備良好的動態性和靈活性；但此類研究偏重于集成算子的定義、計算公式推導、性質、應用范圍及特點分析，少部分算子的計算結果缺乏封閉性，所提出的決策方法往往假設決策者權重或屬性權重完全已知，較少涉及如何確定決策權重的問題。其次，所提出的Pythagorean模糊多屬性決策方法中使用到的距離測度往往是對直覺模糊集的歐式距離、Hamming距離等的平行推廣，當對各備選方案與正理想解、負理想解或其他參考點進行偏差度量時，容易造成逆序情形的發生，即通過計算各備選方案與正理想解的距離測度所得排序結果，同各備選方案與負理想解的距離測度所得排序結果并不一致，甚至兩種優劣次序存在較為明顯的差異。再次，模糊熵尚未充分擴展到Pythagorean模糊多屬性決策方法中，已有研究通過定義Pythagorean模糊熵確定屬性權重，亦或是根據各方案與正、負理想方案的相對熵，構建所有方案滿意度最大化的規劃模型確定屬性權重，但基于Pythagorean模糊熵的偏差度量仍然會產生逆序問題，也在一定程度上造成決策信息的損失。

鑒于以上分析，本文通過定義Pythagorean模糊對稱交叉熵取代歐式距離等距離測度來度量各方案與正、負理想方案的偏差，有效規避兩種方案排序結果不一致的不合理現象，將Pythagorean模糊數之間的對稱交叉熵納入灰色關聯貢獻度的計算，以確定各屬性權重；通過各備選方案到正、負理想方案的標準化加權投影，由雙向投影構造貼近度獲取各方案優劣次序，從而提出一種基于Pythagorean模糊對稱交叉熵及標準化加權投影的多屬性決策方法。

1 基本概念

（1）若s(α1)＞s(α2)，則α1＞α2；

（2）若s(α1)＜s(α2)，則α1＜α2；

（3）若s(α1)=s(α2)，則 比 較π1和π2的 大 小，當π1＞π2，則α1＜α2；當π1＜π2，則α1＞α2。

該得分函數兼顧決策參與者的從眾心理，同時將隸屬度、非隸屬度和猶豫度納入Pythagorean模糊數之間大小的比較，無需通過精確函數進行二次比較，避免出現與直覺相悖的比較結果，具有較強的區分能力。

2 Pythagorean模糊對稱交叉熵

根據Pythagorean模糊集A、B的定義，易知H(A,B)≥0，H(A,B)=0當且僅當A=B；但很顯然，A到B的Pythagorean模糊交叉熵并不滿足對稱性，即H(A,B)一般不等于H(B,A)，因此，H(A,B)雖可作為兩個Pythagorean模糊集A、B之間差異程度的度量，但H(A,B)并不是兩個Pythagorean模糊集之間真正的距離。在定義4的基礎上，同理可定義如下Pythagorean模糊集B到A的模糊交叉熵：

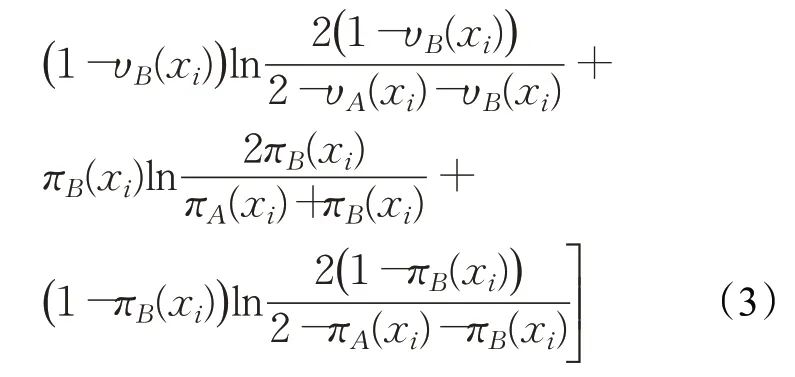
從而得到如下包含H(A,B)和H(B,A)且滿足對稱性的Pythagorean模糊對稱交叉熵：

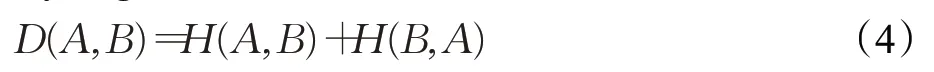
定理1Pythagorean模糊集A與B的對稱交叉熵D(A,B)滿足如下性質：

（1）D(A,B)≥0，D(A,B)=0當且僅當A=B；

（2）D(A,B)=D(B,A)；

（3）D(A,B)≤6n。

證明首先，根據Pythagorean模糊對稱交叉熵的定義，顯然D(A,B)≥0；若已知D(A,B)=0，則必有H(A,B)=0且H(B,A)=0，從而可得A=B；反過來，若A=B，則有H(A,B)=H(B,A)=0，那么D(A,B)=0。其次，根據式（2）～式（4），顯然有D(A,B)=D(B,A)成立，從而（1），（2）得證。下面證明（3），由于：

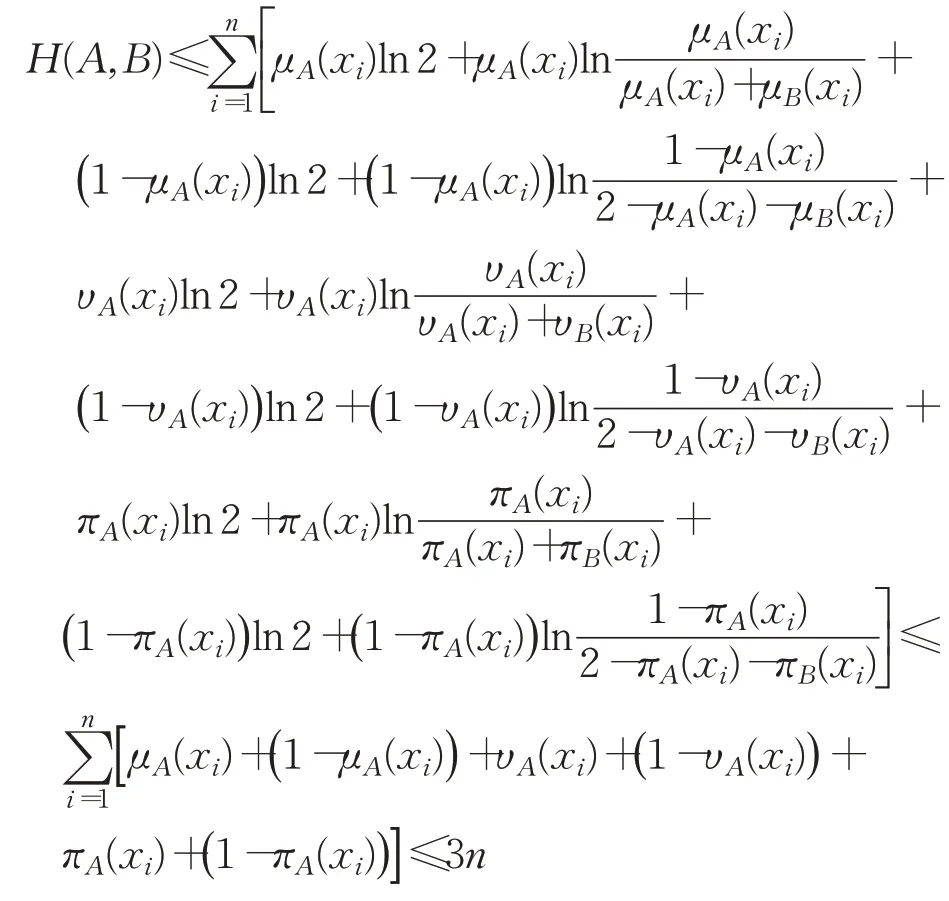
同理，可得H(B,A)≤3n，因此可得D(A,B)≤6n，從而（3）得證。

由Pythagorean模糊集A與B的對稱交叉熵D(A,B)的定義及性質，可知D(A,B)不僅是A與B之間偏差程度的度量，且滿足對稱性和有界性，能夠避免出現A或B→{ 0,1),…,(0,1)}（或{(1,0),…,(1,0)}）時交叉熵的值趨向于無窮大的情況。

定理2Pythagorean模糊集A與B的加權對稱交叉熵Dω(A,B)滿足如下性質：

（1）Dω(A,B)≥0，Dω(A,B)=0當且僅當A=B；

（2）Dω(A,B)=Dω(B,A)；

（3）Dω(A,B)≤6。

證明其中（1）、（2）與定理1類似，顯然成立。對性質（3），有：

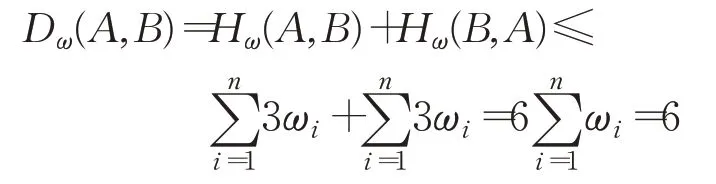
即（3）成立。

3 基于Pythagorean模糊對稱交叉熵及標準化加權投影的多屬性決策方法

3.1 基于Pythagorean模糊對稱交叉熵及灰關聯確定屬性權重

針對決策專家給出的Pythagorean模糊決策矩陣M，設效益型屬性集為I1，成本型屬性集為I2，且C=I1?I2，對各屬性評價信息進行規范化處理，可得：

在PF-TOPSIS法、PF-VIKOR法或其他衡量備選方案差異的多屬性決策方法中，往往采用歐氏距離作為距離測度度量不同方案與理想解的差異程度，容易出現與正理想解距離更近的方案同時與負理想解的距離也更近，也即通過備選方案與正理想解、負理想解的距離測度所得兩種方案排序結果存在差異，導致排序結果并不能真實反映各備選方案的優劣程度。與此相反，由于方案Ai與正理想方案A+、負理想方案A-的Pythagorean模糊對稱交叉熵滿足對稱性、有界性及三角不等式，排除備選方案Ai本身是正理想方案或負理想方案的特殊情況，通過各方案與正理想方案A+的Pythagorean模糊對稱交叉熵所得方案優劣次序，和各方案與負理想方案A-的Pythagorean模糊對稱交叉熵所得方案優劣次序保持一致，能夠避免出現逆排序的決策結果。因此，將Pythagorean模糊對稱交叉熵替換歐式距離等作為兩個或多個Pythagorean模糊集（數）距離測度的度量具有顯著優勢。以下將Pythagorean模糊對稱交叉熵納入灰色關聯貢獻度分析，并以此確定各屬性權重。

在式（7）基礎上，定義方案Ai與正理想方案A+關于單個屬性Cj的Pythagorean模糊對稱交叉熵為：

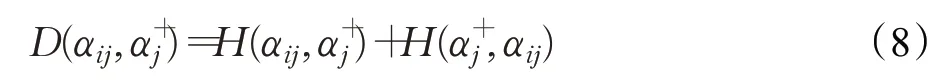
計算方案Ai與正理想方案A+關于屬性Cj的灰色關聯系數為：

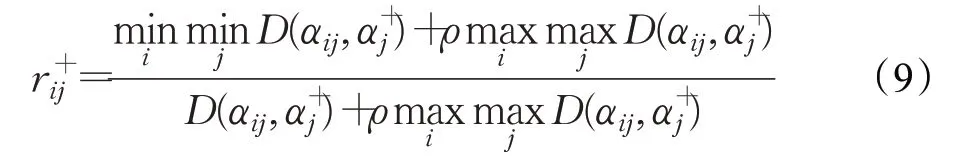
其中，ρ∈[0,1]為分辨系數，通常取值為0.5，其作用在于提高方案Ai與正理想方案A+關于不同屬性評價所得關聯系數之間的差異顯著性。

可得屬性Cj的灰靶貢獻度為：

單個屬性的灰靶貢獻度越大，則該屬性對方案排序的貢獻越大，對方案評價結果的重要程度越大。因此，可依據各屬性的灰靶貢獻度來衡量各屬性的權重大小，灰靶貢獻度越大的屬性，其權重也越大，從而得到屬性Cj的權重為：

3.2 基于標準化加權投影的Pythagorean模糊排序方法

則備選方案Ai在正理想方案A+上的投影可定義為：

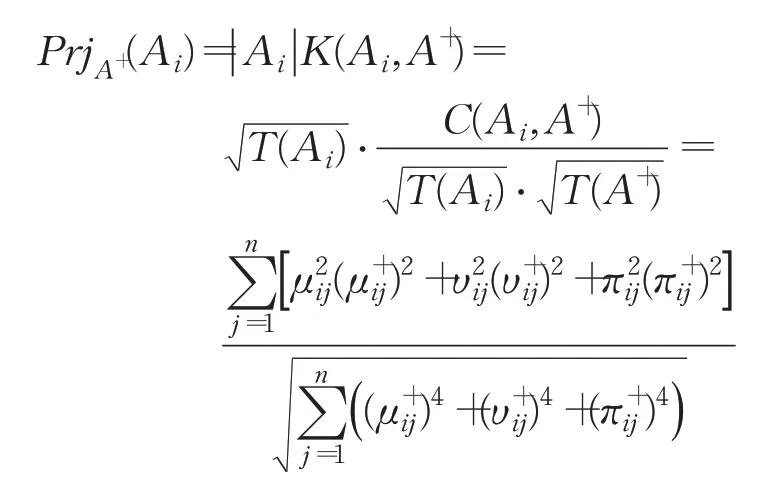
其中，K(Ai,A+)表示備選方案Ai與正理想方案A+的相關系數。

更進一步，考慮到多屬性決策問題中各屬性權重的差異，從而定義備選方案Ai在正理想方案A+上的加權投影為：

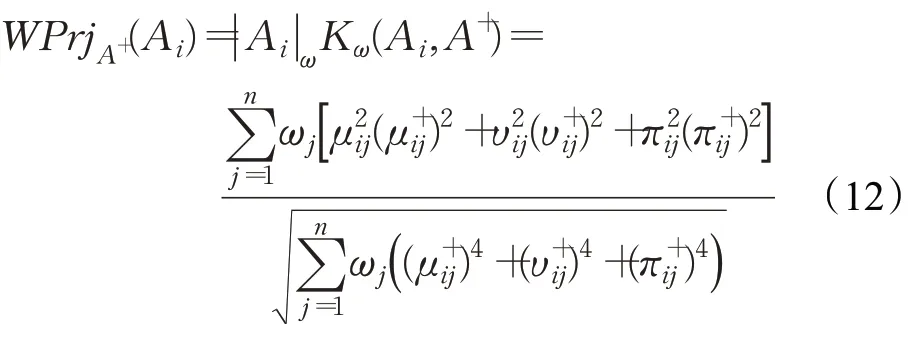
其中，|Ai|ω表示備選方案Ai作為Pythagorean模糊集的加權模，K(Ai,A+)表示備選方案Ai與正理想方案A+的加權相關系數，具體表達式如下：

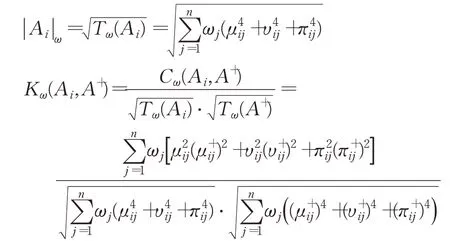
由投影理論在模糊多屬性決策中的應用，可知投影值計算結果可能會出現WPrjA+(A+)＜WPrjA+(Ai)，而從直覺和實際出發，正理想方案A+到自身的投影值應該更大，顯然該結果是不合理的。因此，將式（12）標準化處理，提出如下備選方案Ai在正理想方案A+上的標準化加權投影。

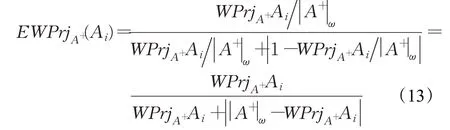
同理，備選方案Ai在負理想方案A-上的標準化加權投影定義為：

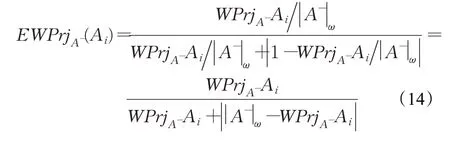
根據以上Pythagorean模糊加權投影和標準化加權投影的定義，可知E WPrjA+(Ai)越大，方案Ai與正理想方案A+越接近；EWPrjA+(Ai)越小，方案Ai與正理想方案A+越遠離。同時，EWPrjA-(Ai)越大，方案與負理想方案A-越接近；EWPrjA-(Ai)越小，方案Ai與負理想方案A-越遠離。由此，定義貼近度為：

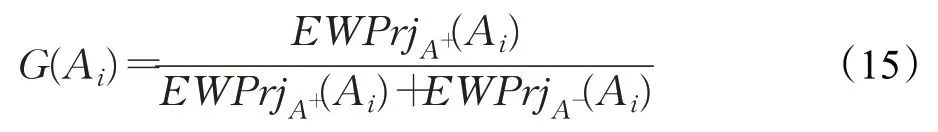
貼近度G(Ai)越大，方案Ai越優，從而得到各備選方案的優劣次序。

3.3 決策步驟

步驟1針對決策者以Pythagorean模糊數對各備選方案關于各屬性開展評價的多屬性決策問題，由式（5）對Pythagorean模糊決策矩陣M進行標準化處理，針對規范化的Pythagorean模糊決策矩陣，由式（1）計算方案Ai(i=1,2,…,m)在屬性Cj(j=1,2,…,n)下Pythagorean模糊值的得分函數，從而由式（6）確定正理想方案A+和負理想方案A-。

步驟2由式（2）～式（4）及式（7）、式（8）計算方案Ai與正理想方案A+的對稱交叉熵，進而由式（9）得到方案Ai與正理想方案A+關于屬性Cj的灰色關聯系數。

步驟3根據式（10）計算屬性Cj的灰靶貢獻度，進一步由式（11）對灰靶貢獻度歸一化處理，并確定各屬性權重。

步驟4由求得的各屬性權重，通過式（12）計算各備選方案在正理想方案上的加權投影值WPrjA+(Ai)，并由式（13）得到標準化加權投影值EWPrjA+(Ai)；進一步，由式（14）計算各備選方案在負理想方案上的標準化加權投影值EWPr jA-(Ai)。

步驟5通過式（15）計算各備選方案的貼近度G(Ai)，并依據貼近度大小對方案排序擇優。

4 實例分析

自我國進入新發展階段，亟需落實新發展理念、構建新發展格局，這就要求新時代的經濟特區要堅定不移實施創新驅動發展戰略，抓住粵港澳大灣區建設重大歷史機遇積極作為，在經濟特區發展中作出新貢獻。假設經濟特區內某政府、高校、科研院所和大型企業，聯合開展規劃設計并謀求合作，從而促進區域經濟高質量發展，其中較為重要的實施途徑是開展一系列的R&D項目。現假設有6個R&D項目可供選擇，記為Ai(i=1,2,…,6)，決策專家擬從技術水平C1、公司和戰略規劃C2、監管機構設置狀況C3、市場發展水平及趨勢C4、財務狀況C5、項目應用前景C6這6個指標展開評估，擬以Pythagorean模糊數給出各備選R&D項目在所有指標下的評價信息，具體如表1所示。

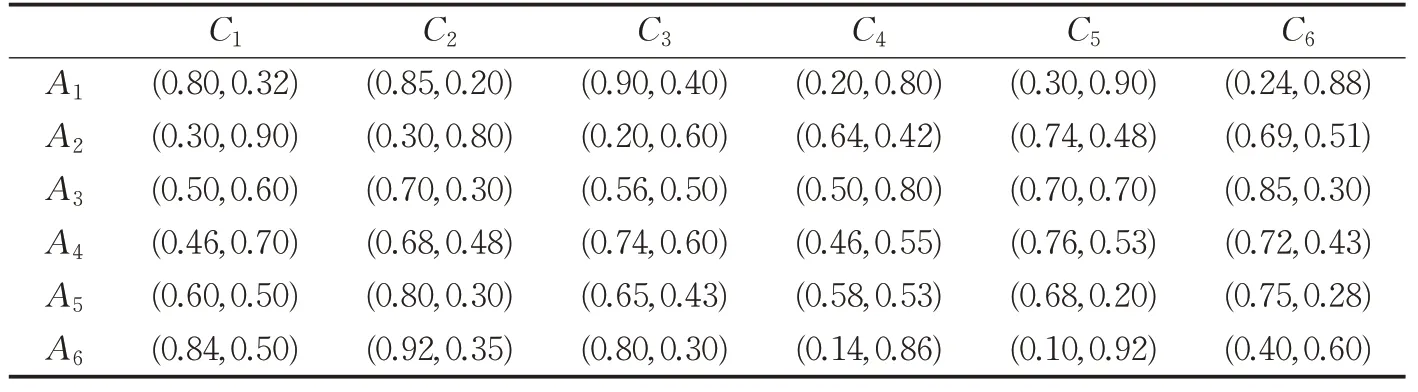
表1 專家提供的Pythagorean模糊評價信息Table 1 Pythagorean fuzzy evaluation information provided by expert

4.1 決策步驟

步驟1由于各屬性均為效益型屬性，無需進行規范化處理，直接由式（1）計算所有Pythagorean模糊評價值的得分函數，并由式（6）得到該決策矩陣的正理想方案A+和負理想方案A-分別為：

步驟2為將Pythagorean模糊交叉熵與灰關聯分析相結合確定各屬性權重，由式（2）計算方案Ai到正理想方案A+的關于屬性Cj的交叉熵H(αij,α+j)，其構成的交叉熵矩陣記為H1；同時由式（3）計算正理想方案A+到方案Ai關于屬性Cj的交叉熵H(α+j,αij)，其構成的交叉熵矩陣記為H2，從而可得：

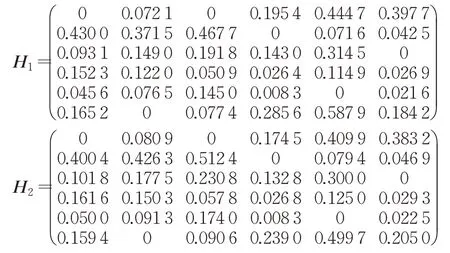
由式（4）、式（7）及式（8）計算方案Ai與正理想方案A+關于屬性Cj對稱交叉熵D(αij,α+j)，其構成的交叉熵矩陣D為：

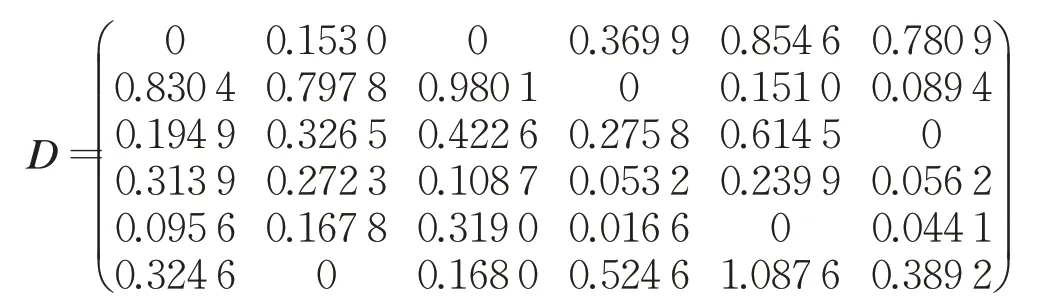
進一步，由式（9）得到各方案與正理想方案A+關于屬性Cj的灰色關聯系數r+ij(i=1,2,…,m;j=1,2,…,n)，其構成的矩陣R+為：

4.2 比較分析

首先，在上述決策步驟4分別計算各備選方案在正理想方案和負理想方案上的加權投影時，使用到各備選方案與正理想方案、負理想方案的加權相關系數，其計算結果分別為：

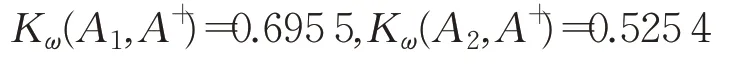
備選方案與正理想方案的加權相關系數越大，方案越優，所得方案排序結果為A5?A4?A3?A1?A6?A2；相反，備選方案與負理想方案的加權相關系數越小，方案排序越靠前，所得方案排序結果為A5?A4?A6?A1?A3?A2。兩種方案排序結果中，前者與本文決策方法在所得結果在A1、A6的排序上存在差異；后者與本文所得結果在A1、A3、A6的排序上存在差異，但最優方案始終是A5且最劣方案始終為A2，驗證了本文決策方法的有效性與合理性。

其次，將文獻[3]提出的PF-TOPSIS法、文獻[31]提出的基于理想解的Pythagorean模糊三支決策方法以及文獻[32]提出的基于新得分函數和累積前景理論的TOPSIS法用于解決本文算例，由各備選方案的貼近度獲取的方案排序結果如表2所示。

表2 不同決策方法下各備選方案的貼近度及排序結果Table 2 Closeness degree and ranking results of all alternatives under different decision-making methods

由上述對比分析結果可知，本文決策方法所得排序結果與文獻[31]、文獻[32]完全一致，與文獻[3]只在方案A1、A6的先后次序上存在差異，其余方案優劣次序也保持一致，相比于這3種決策方法，本文方法在度量各方案與正理想解或負理想解的距離時，采用Pythagorean模糊交叉熵代替歐式距離等距離測度，使得依據所有備選方案與正理想解、負理想解的Pythagorean模糊交叉熵所得兩種排序結果保持一致，不會造成某些方案逆排序現象的發生，決策結果更加科學合理。

再次，將本文決策方法與基于Pythagorean模糊集成算子的多屬性決策方法進行對比分析，主要涉及到PFIWA算子[5]、PFHWG算子[6](γ=0.5)、PFHWA算子[6](γ=0.5)、PFEWG算子[13]、PFWG算子[20]，具體比較情況如表3所示。

由表3可知，5種類型算子所得方案排序結果與本文決策方法所得排序結果雖在部分方案的優劣次序上存在差異，但最優方案始終是A5，再次驗證了本文決策方法的有效性。方案具體排序存在差異，主要是由于本文決策方法與基于不同類型Pythagorean模糊集成算子的多屬性決策方法的決策機制不同；本文方法采用Pythagorean模糊交叉熵取代歐氏距離等距離測度度量各方案與正、負理想解之間的距離，能夠使得與正理想解距離更近的備選方案一定與負理想解的距離更遠，避免產生逆序問題，進而基于灰色關聯貢獻度確定各屬性權重，計算各方案與正、負理想方案的標準化加權投影，通過構造貼近度得到最終決策結果。而基于算子理論的決策方法是通過不同類型的Pythagorean模糊集成算子得到各方案的綜合屬性值（仍以Pythagorean模糊數表示），依據得分函數對各方案排序擇優；例如，PFIWA算子考慮到Pythagorean模糊數中隸屬度和非隸屬度之間可能存在的交叉影響；PFHWG算子和PFHWA算子以Pythagorean模糊Hamacher運算為基礎構造，是一類范圍更廣的t-模和t-余模，是對PFEWG算子和PFWG算子的推廣，更具有一般性；各類算子所包含參數的取值變化體現出決策者主觀判斷或對決策對象風險態度的變化趨勢。相比之下，本文決策方法對方案優劣關系的判斷更為精細，所得方案優劣次序更為穩定，符合實際決策情境。

表3 不同集成算子下各備選方案的綜合屬性值及排序結果Table 3 Comprehensive attribute values and ranking results of each alternative under different integration operators

5 結束語

考慮到傳統歐式距離等距離測度的不足之處，與正理想解的距離更近的備選方案可能與負理想解的距離也更近，即通過各方案與正理想解的偏差大小所得優劣次序和各方案與負理想解的偏差大小所得優劣次序并不一致，導致排序結果并不能真實反映多個備選方案的優劣關系。本文以各備選方案與正理想方案的Pythagorean模糊對稱交叉熵，作為各方案與正理想方案在單個屬性下的評價偏差，通過灰色關聯分析中的屬性貢獻度大小確定各屬性權重；計算各備選方案到正、負理想方案上的加權投影值，將所得兩類加權投影值進行標準化，通過各備選方案與正、負理想方案的標準化加權投影值構造貼近度，最終實現對各方案的排序擇優。下一步，可將Pythagorean模糊對稱交叉熵和加權對稱交叉熵擴展到Pythagorean猶豫模糊集、Pythagorean模糊不確定語言變量等決策環境下，并針對未知的決策者權重或屬性權重，基于Pythagorean模糊對稱交叉熵構建多屬性決策模型，解決相應的多屬性決策問題。