基于有序熵的快遞系統可靠性評價模型與方法

許春梅，孫秉珍

西安電子科技大學 經濟與管理學院，西安 710000

信息技術進步推動了電子商務的迅速發展，2019年，網絡購物交易規模已達10.63億，較上年增長16.4%。其中，8.52億的實物商品交易都需要快遞業務的支撐。研究表明，電子商務與快遞物流業協同發展呈現螺旋式上升趨勢[1]。因此，精準、及時且安全的快遞服務已成為有吸引力的價格、貨真價實的產品外電商競爭力的決定因素。

快遞服務的區域、水平和價格是快遞企業競爭力的三大要素。而相對于路徑優化[2]、車輛調度[3]和選址[4]等研究，對快遞服務水平的研究尚不充分。自Gronroos等[5]提出顧客感知服務質量，以期望與實際感受的差別評價服務后，Parasuraman等[6]將服務質量概念化，提出SERVQUAL量表以理解顧客的服務需求以來，已有許多研究從快遞服務質量評價的角度對快遞企業提供的快遞服務水平進行研究。例如，山紅梅等[7]用云模型研究了快遞服務質量指標的隨機性和模糊性，Kilibarda等[8]通過實證研究了不同市場區段的客戶如何評估貨運代理服務的品質。

已有對快遞服務質量的研究主要集中在評價量表方面，對快遞服務系統可靠性的研究較少，因為快遞服務質量評價量表是科學且易于在實踐中應用的工具。然而，據不完全統計，2016年電商退貨原因中快遞占比高達21.3%，過半的網購者因配送問題放棄購買。由于在快遞配送中，交通事故、惡劣天氣和網絡癱瘓等意外的發生會導致快遞服務的中斷或延遲等情況，使快遞系統可靠性降低，電商企業的破損和運輸等成本上升，損害與消費者的長期關系，因此快遞配送系統是否可靠是電商企業能否提供令人滿意的服務的關鍵之一，從系統可靠性的角度進行研究可以較好地反映快遞企業所提供的快遞服務的綜合水平。

系統可靠性評價方法有隨機過程、蒙特卡洛模擬、遞歸算法等。Lin等[9]基于網絡理論和改進的多色集理論，從故障傳播的角度研究了復雜機電系統的可靠性評估問題。已有研究側重于系統完成功能的能力，而脆性可以刻畫系統穩定運行需要的打擊承受能力來反映系統的可靠性。

韋琦等[10]提出復雜系統的脆性是復雜系統在受到外界的打擊時容易崩潰的性質。近年來，許多學者對系統脆性造成的連鎖崩潰及其應對策略進行了研究。既有理論研究，如Liu等[11]建立了基于脆性理論的多狀態制造系統可靠性分析方法。也有在各個領域的應用研究，在電力領域，針對電網大規模停電和電力系統故障等問題，研究電力系統因脆性支路傳播導致崩潰的機理與應對策略[12]；在供應鏈領域[13]，由脆性概念結構劃分供應鏈層級結構，研究供應鏈系統內外部脆性傳播影響因素及聯系強度；在其他領域亦有相關研究，如管杜鵑等[14]針對項目間交互耦合結構造成的脆性風險提出項目脆性風險控制策略，熊國強等[15]將RDEU博弈模型與脆性理論集成，研究情緒因素影響下城市拆遷由糾紛到對抗沖突的脆性激發過程。已有研究表明，脆性不僅能夠很好地反映復雜系統連鎖崩潰風險，而且有利于提出有效的防控措施與應對策略。已有對系統脆性的研究主要是通過信息熵結合圖論[13]、博弈論[15]等方法模擬脆性激發和傳播的過程，較少關注脆性傳播造成的對系統不同部分的影響程度，這可以通過賦予決策權重來度量。而傳統的專家打分法、AHP等方法容易受到人的主觀性影響，而且眾多的成對比較次數容易造成一致性的降低。而有序熵方法[16]將Shannon熵擴展到脆弱性和模糊的有序分類問題中，降低了成對比較的次數，能夠確保決策權重與結果單調性的一致性。

本文從脆性的角度評價快遞服務質量，通過結合信息熵與有序熵方法，刻畫由于意外事件發生而顯露出來的系統脆性，建立了快遞服務系統可靠性評價模型，并通過案例由脆性因子與子系統的脆性排序評價快遞公司的快遞服務質量。基于有序熵的快遞服務系統可靠性評估模型與方法的研究，一方面為快遞企業服務質量管理決策提供新的決策模型與思路；另一方面也為脆性這一新的視角應用于快遞企業服務質量管理研究進行嘗試和初探。

1 快遞服務系統可靠性評估模型

1.1 快遞系統脆性風險概念模型

韋琦等[10]提出復雜系統的脆性為復雜系統在受到外界的打擊時容易崩潰的性質，且此前沒有任何明顯的征兆。并提出復雜系統脆性結構模型是由脆性風險值（系統崩潰）、系統結構、脆性事件、脆性因子組成的四層結構。

本文從脆性的角度對快遞系統進行分析，將系統的脆性風險來源劃分為系統、子系統、脆性事件和脆性因子四個層次，建立快遞系統脆性風險結構概念模型。因為系統的復雜性與整體性，所以將系統按層次逐級劃分進行復雜系統脆性風險來源的分析。通過將系統劃分為子系統反映系統的組成、結構和其內部各部分的層次關系等。由于脆性是由意外發生的事件觸發，不同的事件會影響到不同的子系統，因此從脆性的角度將子系統的下一級定為脆性事件。通過將脆性事件劃分為脆性因子，來深入分析脆性事件發生的影響因素和有針對性地提出預防措施。

1.2 快遞服務系統可靠性評估模型

信息熵是以某種概率發生的事件的樣本空間的不確定性程度，可以刻畫脆性事件集合導致子系統發生崩潰的不確定性程度，有序熵可以表達屬性排序起伏程度，二者結合建立子系統與系統脆性因子的排序規則。

本節涉及的變量及其含義如表1所示。

表1 相關變量符號及含義Table 1 Symbols and meanings of related variables

定義1[10]設S={S1,S2,…,Sn}為子系統集合，L={l1,l2,…,lm}為脆性事件集合，脆性事件發生的概率為P(lk)。定義由脆性事件導致子系統Sj崩潰的不確定性程度為：

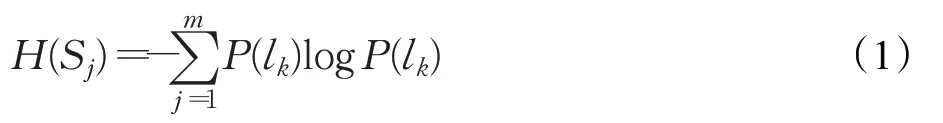
性質1系統脆性熵的非負性。

證明由0≤P(lk)≤1可得logP(lk)≤0，進而可得H(Sj)≥0。當且僅當P(lk)=0或1時，才有H(Sj)=0。

性質2系統脆性熵的傳遞性。

若H(Si)≤H(Sm)，H(Sm)≤H(Sj)，則H(Si)≤H(Sj)。

證明由H(Si)≤H(Sm)，H(Sm)≤H(Sj)，得H(Si)-H(Sm)≤0，H(Sm)-H(Sj)≤0，兩式相加可得H(Si)-H(Sj)≤0，即H(Si)≤H(Sj)。

上面介紹了信息熵，對導致子系統崩潰的脆性事件集合的不確定性程度進行了刻畫。事實上系統崩潰的可能性不僅取決于子系統崩潰的可能性，還與子系統作為系統的組成部分的重要程度有關。有序熵能很好地刻畫數據的單調性關系的同時表明數據對決策的預測能力，減少轉化過程中的信息損失。因此，下文用有序熵定義脆性因子和子系統層面的脆性系數，刻畫存在單調性關系的多屬性決策中相應數據對決策的預測能力，即其對最終決策的影響程度。

根據脆性因子與脆性風險成正比或反比關系將其分為正脆性因子和負脆性因子，用正向有序熵表示正脆性因子系數和用負向有序熵表示負脆性因子系數在意義上是等價的。

定義2設S={S1,S2,…,Sn}為子系統集合，Y={y1,y2,…,yd}為脆性因子集合，A?Y，F?Y。對于?yt∈Y，定義脆性因子yt的系數RHy為：

設脆性因子的脆性權重集合W={w1,w2,…,wd}。脆性因子的有序熵越大，表示其不確定性程度越大，則對子系統發生脆性風險的影響就越大，因此脆性因子的脆性權重可由其脆性系數RHyt經歸一化得到。

子系統脆性系數RHj由子系統Sj在每一個脆性因子下的有序熵集成，而脆性因子本身對決策的影響力（權重）也不同，因此子系統脆性系數由該子系統各脆性因子的脆性因子系數與脆性權重的乘積和得到。

定義4設S={S1,S2,…,Sn}為子系統集合，W={w1,w2,…,wd}為脆性因子權重集合，Y={y1,y2,…,yd}為脆性因子集合，A={y1,y2,…,ya}、F={y1,y2,…,yf}分別為正、負脆性因子集合。對于?ya∈A，?yf∈F，定義子系統脆性系數RHj為：

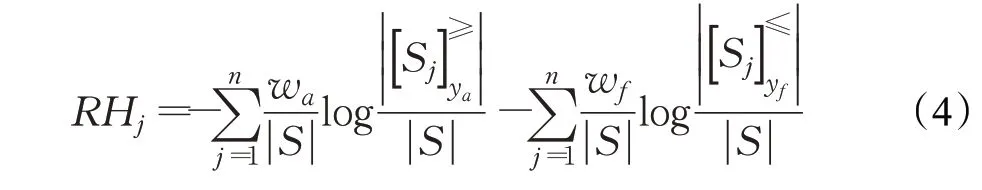
子系統脆性系數表明脆性因子層面表達的對決策的預測能力，而子系統脆性熵在脆性事件層面表達子系統內脆性事件發生的不確定性程度，因此通過脆性系數與脆性熵的乘積和可以表明子系統在系統中的重要程度。

定義5設S={S1,S2,…,Sn}為子系統集合，對于?Sj∈S，定義子系統的脆度為：

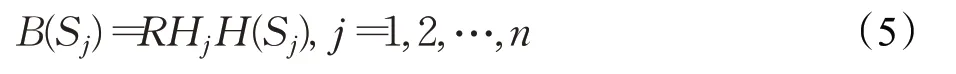
復雜系統脆度不僅要考慮子系統的脆度，還要考慮子系統在復雜系統中的任務承擔比例，用子系統承擔的流量占復雜系統流量的比例表示。

基于上述定義，構建快遞企業服務系統可靠性評價理論模型。首先將處理收集到的脆性因子數據，得到T時期脆性因子——子系統矩陣Mt，接著根據脆性因子的分類，對矩陣Mt中的元素應用有序熵方法計算得到脆性因子系數矩陣RHyt與脆性因子的脆性權重wt，結合得到子系統脆性系數R Hj，再與由脆性事件概率計算得到的子系統脆性熵相乘得到子系統脆度，最后根據系統與子系統的邏輯結構關系，得到系統脆度。

2 案例分析

考慮代表性和數據可得性，選取快遞公司為S1順豐、S2申通、S3圓通、S4韻達、S5郵政。收集國家郵政局官方統計數據、企業經營簡報和文獻中的部分調查數據，進行案例分析。根據國家郵政局官網的郵政業消費者申訴情況通告，將投訴的主要事件作為脆性事件。結合參考文獻[17]快遞企業競爭力的決定因素，選取與投遞服務水平有關的年營業額、業務增幅、網絡覆蓋率和投遞服務有效申訴率，對違規收費選取價格水準并考慮到實際中快遞網點定價靈活性加入價格彈性，分別用丟失有效申訴率、延誤有效申訴率、損毀有效申訴率和收寄服務有效投訴率來反映快遞公司對對應各類事件的處理水平和應對能力，加入保價費用反映客戶對快遞損毀的心理預期接受能力。

設子系統集合為S={S1,S2,S3,S4,S5}，脆性事件集合為L={l1,l2,l3,l4,l5,l6}，脆性因子集合為Y={y1,y2,…,y11}，具體含義見表2。

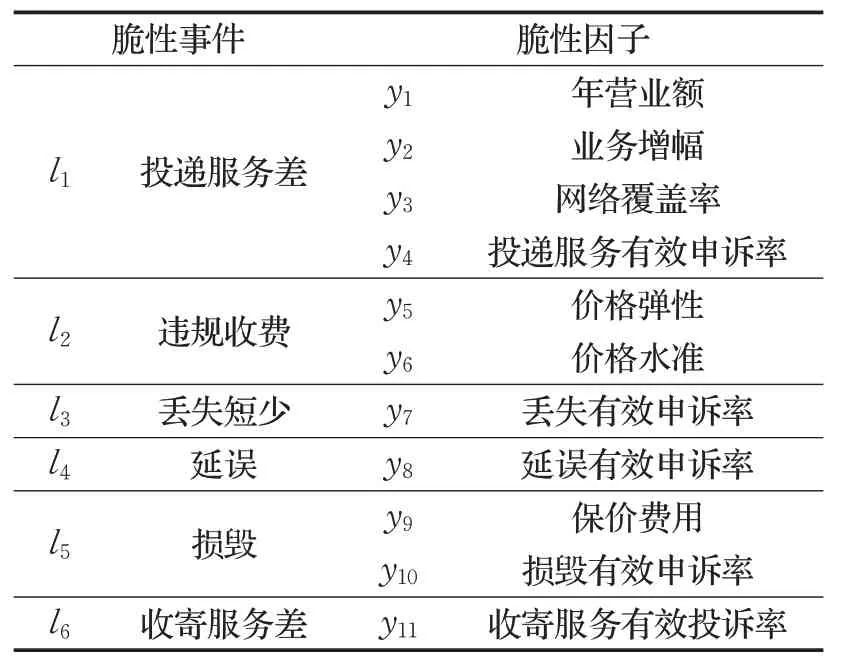
表2 脆性事件及脆性因子符號及含義Table 2 Brittleness events and brittleness factors

由相關數據得9月脆性因子——子系統矩陣M9：

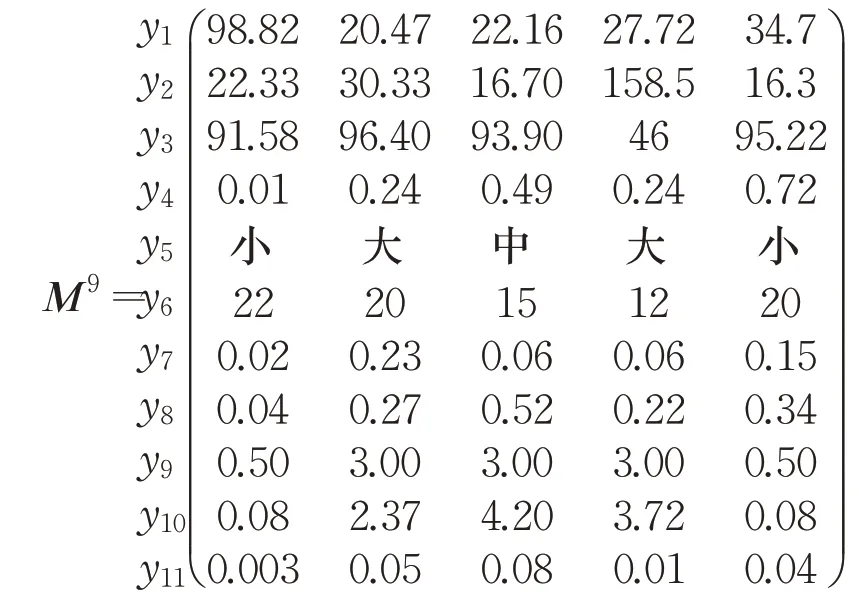
劃分y4、y6～y11為正脆性因子，y1、y2、y3和y5為負脆性因子。由有序熵得T月的脆性因子系數矩陣9月脆性因子系數矩陣為：

類似地，可得到7、8月的相應矩陣。取7、8、9三個月的矩陣值均值計算脆性因子權重與子系統脆性系數，然后應用有序熵方法，由式（3）得脆性因子的脆性權重wt分別為0.103，0.103，0.103，0.103，0.074，0.090，0.097，0.097，0.048，0.092，0.089，排序結果為w1=w2=w3=w4＞w7=w8＞w10＞w6＞w11＞w5＞w9。因此，營業額、業務增幅、網絡覆蓋率和投遞服務有效申訴率是決定系統脆性的最重要的脆性因子，丟失、延誤、損毀等問題對脆性影響次之，收寄服務、價格水準、價格彈性和保價費用影響較小。這說明從長遠來看，價格對大部分客戶來說不再重要，價格競爭并不能顯著提高快遞系統可靠性與企業競爭力，而增強營業額、業務增幅、網絡覆蓋率和投遞服務有效申訴率代表的企業綜合實力、發展潛力與顧客服務能力，能夠提升快遞公司的可靠性并獲得可持續競爭優勢。

由國家郵政總局發布的快遞業情況中每家快遞各類情況的投訴數量占總投訴數量（以算例中涉及的快遞公司各類投訴數量為總體樣本）的比例作為各類脆性事件發生概率，如表3所示。

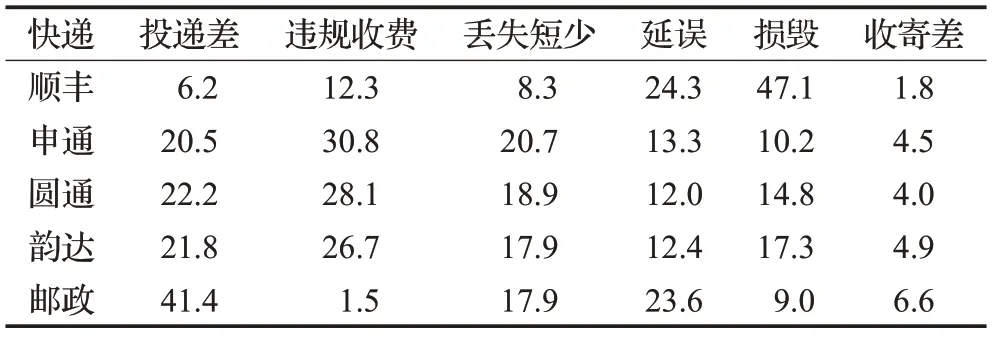
表3 子系統-脆性事件概率Table 3 Subsystem-brittle event probability %

快遞子系統脆性系數RHj、脆性熵H、脆度B排名，《2020年快遞品牌服務滿意度排行榜》的排名以及通過AHP、灰關聯熵[17]方法的排名如表4所示。

表4 快遞企業脆性排序結果Table 4 Express enterprise brittleness sorting results

由表4可知，應用本文模型、傳統AHP與灰關聯熵方法[17]的排序結果都是B(S4)＜B(S1)＜B(S2)＜B(S3)＜B(S5)，排序結果的一致性說明了本文模型排序結果的有效性與可行性。而在排序結果有效的前提下，本文所構建的模型結合信息熵與有序熵方法，比起AHP方法所需的成對比較次數更少，比起灰聯系度方法能夠保留數據的偏序信息，而且能夠在降低人為主觀因素影響的同時考慮模糊性指標的影響。由模型相關定義可知，子系統脆度越高，說明脆性風險越大，可靠性越低。因此可以判斷韻達、順豐可靠性最強，申通、圓通可靠性較強，郵政可靠性最弱，排序和實際情況中人們對快遞公司的滿意度比較吻合。

關于脆度與滿意度排名的差異，郵政快遞雖然速度較慢價格較高，但其業務范圍廣泛，在其他快遞未涉及的邊遠地區亦有布局，加上較為規范的網點建設與服務，因此郵政雖然脆性最大但滿意度略優于圓通。韻達滿意度居中但脆度最小是由于其雖然起步較晚，體量及營收不如順豐等快遞，但是韻達率先實現全部自營中轉中心并針對服務派件模式做出調整，加上韻達快遞本身營業收入總額較少，導致其7～9月業務增幅大幅度增長，遠超其他快遞公司，同時使韻達快遞7～9月的投訴率小幅度下降，相對于其他快遞公司相對穩定的投訴率來說處于較低水平等。相當于一個另類的脆性事件的發生帶來的脆性因子層面等連鎖反應使韻達快遞的脆性降低，提供的快遞服務可靠性增強，進一步說明了模型的有效性。

快遞系統的脆度不僅要考慮子系統的脆度還要考慮其承擔的快遞量。快遞子系統承擔業務量如表5。

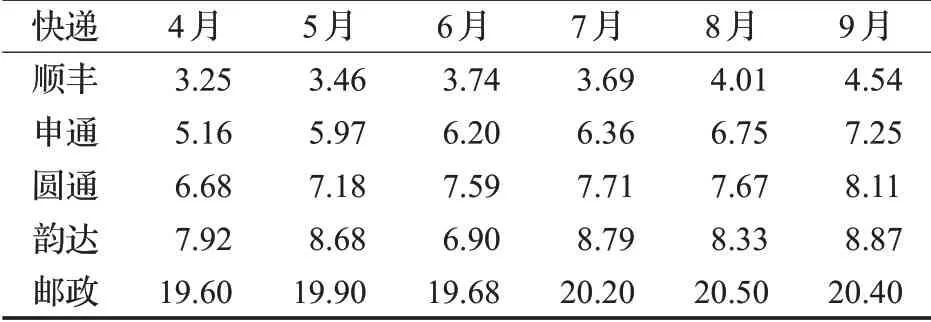
表5 各快遞公司4～9月快遞業務量Table 5 Volume of express delivery from April to September of each express company

由式（6）得快遞服務系統脆度為：

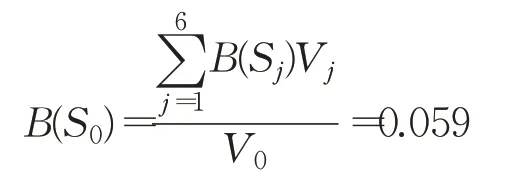
比較可知，順豐、申通、圓通等子系統脆度都低于行業平均水平，表現出較高的可靠性，韻達脆度較低，體現出有效改革對企業可靠性提升的顯著作用，郵政脆度高出平均水平較多，說明其亟需提升可靠性。

綜上所述，排名靠后的快遞企業可以通過針對營業額、業務增幅、網絡覆蓋率和投遞服務有效申訴率四個關鍵脆性因子進行集中改善，在不斷建設優化倉儲運輸網絡等提升企業實力的同時增強快遞服務意識，規范化人員培訓，將顧客感知服務質量擺到重要位置等方式增強可靠性。

3 結束語

快遞服務系統可靠性是社會物流系統可靠性的反映，對依賴快遞運送產品的電子商務企業來說，選擇更可靠的快遞公司，進而為客戶提供精準、及時、安全和穩定的快遞服務，能夠提升顧客滿意度。

本文從可能使快遞配送環節崩潰的脆性事件出發，解析得到使其發生的影響因素即脆性因子，建立基于有序熵的快遞服務系統可靠性評價模型。通過對脆性因子脆度排序，為快遞公司在諸多脆性影響因素的改善順序和著重點方面提供參考；通過子系統脆度排序，為電商企業選擇可靠的快遞公司提供建議；通過對子系統脆度和快遞服務系統脆度的比較，挖掘企業盈利背后的潛在憂患，對于快遞企業可持續良好運行有一定的借鑒意義。

同時，本文也存在一些不足。數據的可得性與數據量限制導致結果存在一定的偶然性和誤差性。再者，本文將子系統視為相對獨立的，不考慮子系統間聯系影響，而復雜系統存在復雜性和開放性等特性，系統與外界環境、內部各子系統間、子系統與外界環境間都存在物質與能量交換，因此未來可對子系統間的脆性聯系進行研究，通過圖論、博弈論和集對分析等理論與方法刻畫子系統間的相互影響及其程度。