廣義薄膜方程的數值求解
賀裕 付寶君 楊雨婷
(哈爾濱師范大學 黑龍江哈爾濱 150025)
近年來,由于電子控制與檢測水平的迅速發展,新型制膜技術不斷涌現,薄膜技術和薄膜材料也開始成為真空技術和材料科學等領域備受矚目的重要研究領域,薄膜科學已逐漸成為一門研究薄膜生產技術、生長原理、物性分析方法與控制的科學[1]。在使用外延生長技術制備薄膜時,沉積原子會落在襯底表面上,并通過某一種方式相遇到一起,從而產生一些原子團。隨著新原子的不斷加入,這些原子團逐漸長大變成較大的粒子簇,人們將這種粒子簇稱為“島”。隨著沉積過程的持續進行,原子島不斷生長,當原子島長到一定階段時,在原子島內部相互連接,形成通道網絡結構。在沉積不斷進行時,原子填補通道之間的空隙,形成連續薄膜[2]。薄膜生長過程是比較復雜的原子活動,涉及沉積原子經歷的各種動力學過程,包括原子間擴散的動力學過程、原子團擴散的動力學過程和多層膜生長的動力學過程。
眾所周知,四階薄膜方程可描述相變、薄膜增長等物理過程,并且都可用如下形式來描述:
其中,Ω ?RN為具有光滑邊界?Ω 的有界區域,T為正數,p>1,u=u(x,t)表示薄膜表面的高度。相關文獻[3]構造了方程(1)的弱解,并證明其存在唯一性。
當N=1 時,方程(1)為廣義薄膜方程[4],近年來被廣泛研究。
當p=2 時,方程(1)稱為Cahn-Hilliard 方程[5],最初用于表達了分離過程中守恒濃度場的演化,如今已成為材料科學和工程的支柱。這個方程也支持在圖像分析中用來提高模糊圖像清晰度的方法。相關文獻[6]描述了Cahn-Hilliard方程在放射性資源采集與遷移建模中的應用。
相關文獻[7]提出了描述薄膜外延生長的能量守恒方程:
ut=g-?·j+η
Zangwill 提出薄膜表面的高度函數u(x,t)滿足周期邊值條件和某種初值條件[8]。相關文獻[9]利用Galerkin 逼近得到了弱解。King 等人利用半離散逼近思想,證明了外延薄膜生長初邊值問題在適當函數空間中弱解的存在性、唯一性和正則性,同時導出解的長時間行為[10]。
本文主要研究以下初邊值條件的廣義薄膜方程問題:
并簡要論述一些基本概念和定義,以及求解方程的時間差分、再生核樣條函數法(RKSM),隨后,給出了所提方法的理論分析,最后,數值算例驗證了算法的有效性。
1 相關理論
定義3[11]Wm[a,b]=u(x)|u(x)(m-1)在[a,b]上絕對連續,u(x)(m)∈L2[a,b],其內積定義為:
則,Wm[a,b]是再生核空間。
定理3[11]再生核空間Wm[a,b]的再生核函數為:
定理4[12]再生核空間Wm[a,b]的再生核函數Rm(x,y)關于變量x是2m-1階樣條。
針對此問題,構造再生核空間W5[a,b],在此空間對方程進行討論,并取W3[a,b]中的再生核函數作為5次樣條的一部分基底,然后,運用配置法,對方程的精確解進行數值逼近,并將全面系統地對本文構造的再生核樣條法進行理論分析,對數值解的一致收斂性進行嚴格地證明,最后給出數值算例來驗證該算法的有效性。
2 再生核樣條函數法的具體求解過程
證明:設存在不全為0 的數c1、c2、c3、c4、…cn+5,使得:
取pj(x) ∈W5[a,b],滿足:
且p(ji)(a)=p(ji)(b)=0,i=0,1…5;j=5。
由內積定義(3),將式(5)兩邊分別與pj(x)做內積,可得:
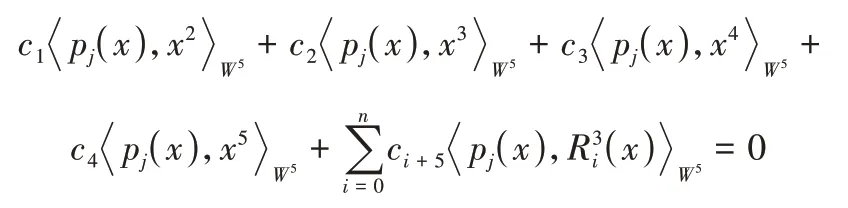
容易求得ci+5=0(i=0,1…n),而{x2,x3,x4,x5}顯然線性無關,有c1=c2=c3=c4=0。
設矩形域={(x,t)|a≤x≤b,0≤t≤T},取空間步長h=(a=x0<x1<…<xM=b),即x=xk=a+(k=0,1,…M);時間步長τ=(0=t0<t1<…<tT=T),即t=tn=nτ(n=0,1,…N)。其中,N,M都是正整數。用兩族平行直線t=tn=nτ和x=xk=a+將矩形域進行網格剖分,網格節點記為(xk,tn)。
以下是對時間變量進行差分,格式如下:
其中,un表示第n 個時間層上的函數,即un=u(x,tn),代入方程(1),整理得:
近似解un(x)有如下表示形式:
在配置點xk=a+(k=0,1,…,M)上進行計算,使用配置法來獲取un(x),它的系數a1、a2、…aN+5滿足:
引入矩陣U=(a1,a2,…aN+5),則式(9)、式(10)、式(11)轉化成矩陣方程:
其中,C為系數矩陣,B為常數項。且C非奇異,因此,un(x)存在且唯一。
3 理論分析
定理6:設u(x,tn)是方程(2)的精確解,un(x,tn)是u(x,tn) 的近似解,則un(x,tn) 和它的各階導數u(k)(x,tn)一致收斂于精確解u(x,tn)及其各階導數
證明:令R(x,y)是再生核空間W5[a,b]的再生核函數。由:
有:
而再生核函數在[a,b]是連續的,因此:
|u(x,tn)-un(x,tn)|≤M‖u-un‖→0
其中,常數M=‖Rx‖≥0。
即:un(x,tn)一致收斂于u(x,tn)。
其中,常數Mk=≥0(k=1,2,3,4)。因此,各階導數u(k)(x,tn)一致收斂于u(nk)(x,tn)。
4 數值算例
例:考慮如下廣義薄膜方程的初邊值問題[13]。
其中,p分別取2,3,4,5,6,其精確解u(x,t)=ex+x+(t-2)。
取M=10,N=10,xk=(k=0,1,2…,10),tn=(n=0,1,2…,10),用文中的方法計算的最大絕對誤差和最大相對誤差見表1。
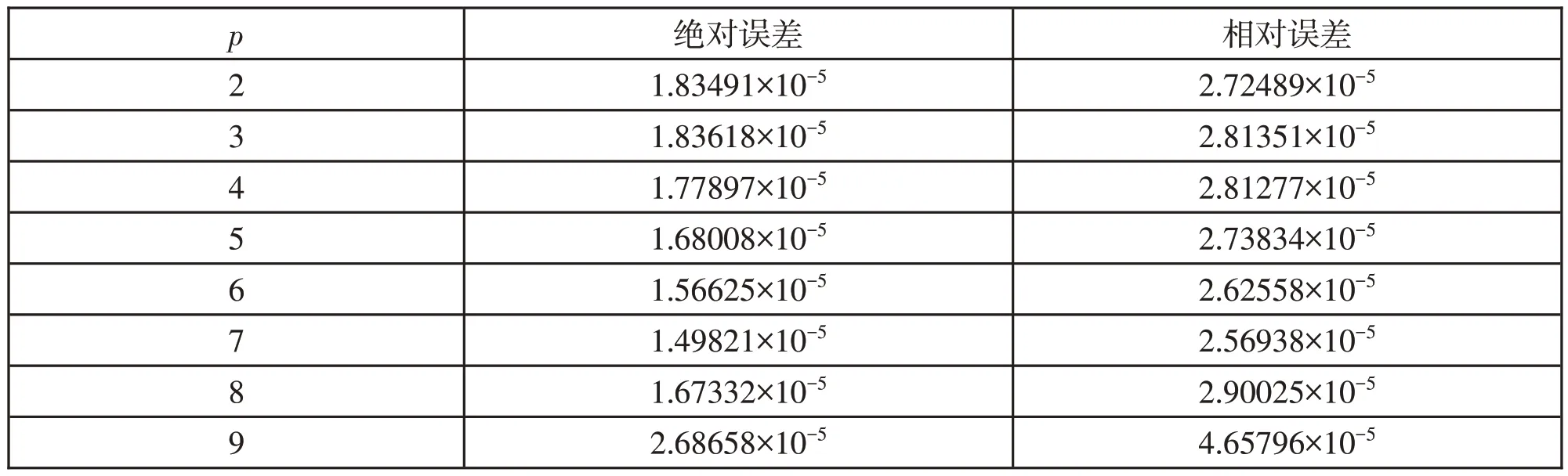
表1 方程(12)中p 取不同值的最大絕對誤差和相對誤差

